乙醇偶合制備C4烯烴的生產參數研究

王桂旭，楊曾欣

（西安電子科技大學 電子工程學院，西安 710126）

C4烯烴的生產一般通過化石能源的裂解、餾分得到，其依賴于石油資源，會造成對環境的嚴重污染。隨著有機化工技術的發展，C4烯烴也可以通過乙醇偶合反應制得，而乙醇資源更為便宜與豐富，對環境污染更小，有更高的經濟價值。

本文根據2021年全國大學生數學建模大賽B題的數據，研究催化劑組合與溫度對乙醇轉化率、C4烯烴選擇性的影響關系，并以C4烯烴收率為優化目標，計算最佳的生產參數。

1 模型準備

為了定量分析問題，首先提取“催化劑組合”中蘊含的數字信息，并作出符號標記，見表1。然后提取乙醇轉化率、C4烯烴選擇性，刪除其余無關的特征。最后針對特殊催化劑組合A11，因為與其他組合相比，沒有催化劑載體HAP，并且數據量只有一組，所以暫時刪除此組。

表1 變量的符號標記

其中，Co/SiO2與HAP質量比，C4烯烴收率滿足以下數量關系：

2 模型建立與求解

2.1 嶺回歸模型

為了探索各個因變量對乙醇轉化率、C4烯烴選擇性的影響關系，可以通過嶺回歸線性模型（Ridge Regression）分別對兩者進行回歸分析。模型可表示為：

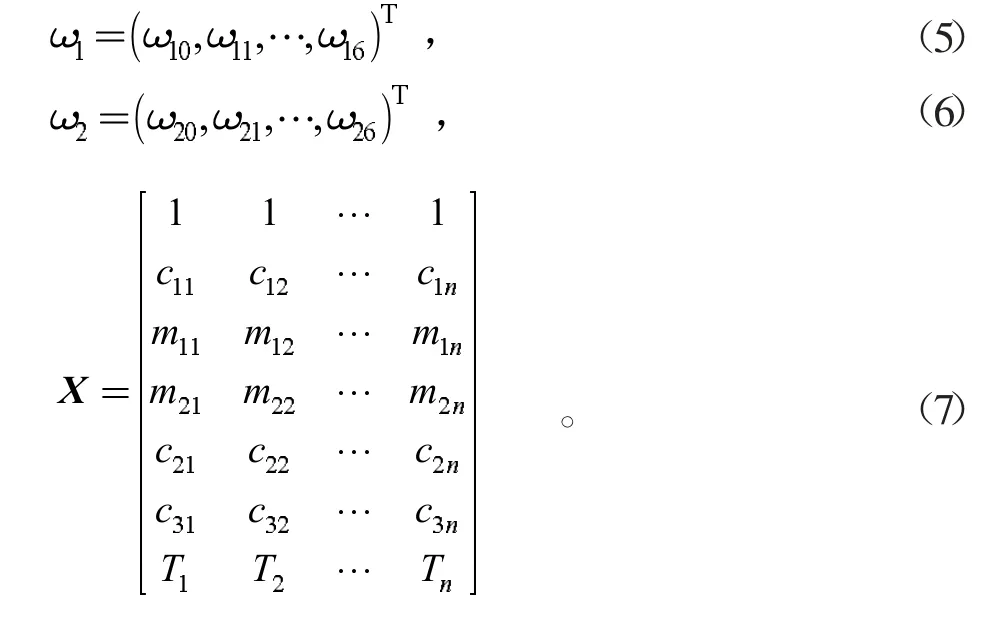
回歸系數可通過式（8）、式（9）得到。

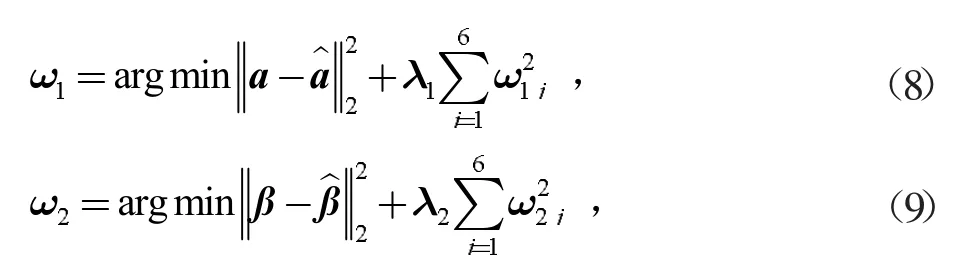
式中：向量α、β分別代表乙醇轉化率與C4烯烴選擇性的真實值，正則化系數λ1、λ2代表L2正則化強度，其值越大，模型的穩健性越好，不容易受到共線性變量的影響。

2.1.1 判斷共線性

為了檢查模型是否受到共線性變量的影響，正則化系數λ1、λ2可以先設置一個較小值，如10-3。先對數據進行分割，一部分作訓練集，另一部分作測試集，然后對訓練集進行嶺回歸分析，得到兩者的決定系數分別為。由于各個變量間的范圍、量綱不同，需要對回歸系數進行歸一化，可將變量的回歸系數乘以變量對應的標準差。

運用交叉驗證對訓練集重復計算5次，可以得到回歸系數的變化范圍，如圖1所示。

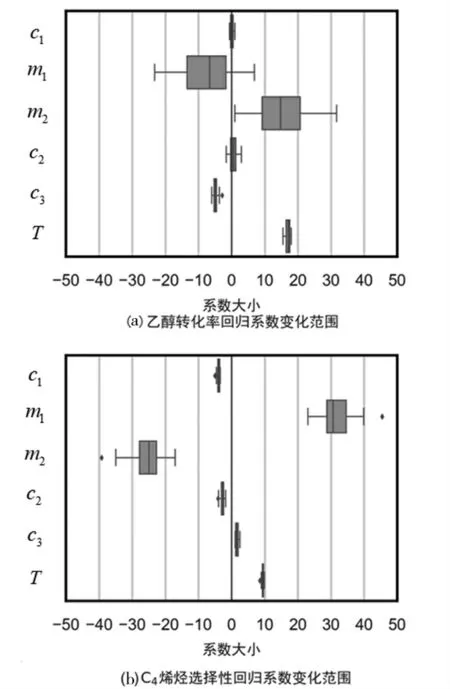
圖1 回歸系數變化范圍

由圖1中可以看出，m1、m2的回歸系數變化范圍較大，存在一定程度的相關關系，即m1、m2共線性。由式（1）知Co/SiO2與HAP質量比與Co/SiO2質量、HAP質量存在關系，因此剔除回歸變量c2，對訓練集重新進行回歸，檢驗回歸系數的變化范圍，如圖2所示。

在圖2中，m1、m2的回歸系數變化范圍相較圖1更小，說明剔除共線性變量c2后，模型的穩健性更好。

圖2 排除共線性后的回歸系數變化范圍

2.1.2 優化正則化系數

在一定范圍內對正則化系數進行窮舉搜索，使用留一法（leave-One-Out）進行交叉驗證，即在訓練集中每次只校驗1個數據，訓練其余所有數據，得到每個系數每次訓練的均方誤差（Mean Squared Error，MSE），再計算其均值得到每個系數對應的均方誤差。再篩選出最小均方誤差，其對應于最優正則化系數。最后，得到λ1=3.852 1，λ2=11.189 5，乙醇轉化率、C4烯烴選擇性的回歸系數如圖3和圖4所示。

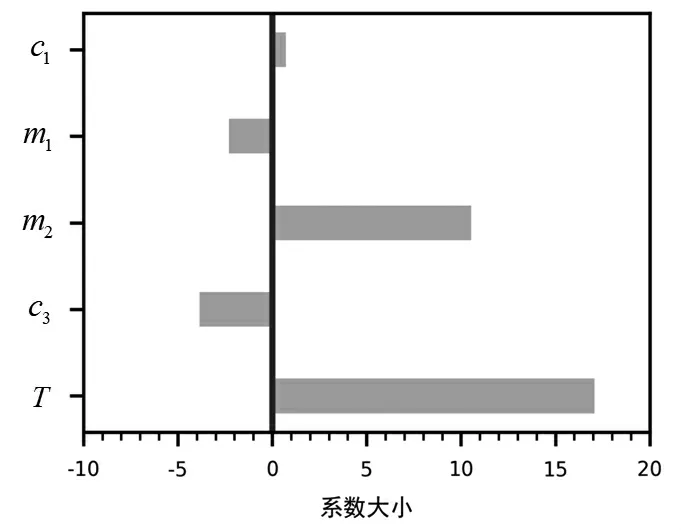
圖3 乙醇轉化率的回歸系數

圖4 C4烯烴選擇性的回歸系數

比較各變量標準化回歸系數的大小，可以發現溫度、載體HAP質量與乙醇轉化率呈強正相關，而催化劑Co/SiO2質量、乙醇濃度與其呈負相關。同理，溫度、催化劑Co/SiO2質量與C4烯烴選擇性呈強正相關，而Co負載量、載體HAP質量與其呈負相關。其中，溫度對乙醇轉化率與C4烯烴選擇性的變化是一致的，溫度越高，兩者的值都越大；而Co負載量、催化劑Co/SiO2、載體HAP的質量與乙醇含量在兩者的變化是相反的。并且溫度的標準化回歸系數是最大的，說明對兩者的影響程度也是最大的，因此在合適的調節范圍內，應盡可能使反應溫度達到最大。

2.2 多層感知機

為了優化生產參數，提高C4烯烴收率，需要對乙醇轉化率與C4烯烴選擇性作出更精確的預測。一般的線性回歸模型無法適應復雜的模式，可解釋的方差如前面3.1所述，只能達到70%左右，應該使用非線性模型，如多層感知機（Multilayer Perceptron），對生產結果進行回歸。

2.2.1 網絡結構

多層感知機模型利用全連接網絡發現復雜的模式，網絡的層數、神經元個數越多，探索復雜模式的能力越強大。在相鄰兩層網絡中，后一層網絡的輸出與前一層的輸入滿足

式中：Xi+1表示第i+1輸出；Xi表示第i層輸入；Wi、bi分別是2層之間的權重矩陣與偏置向量；f（*）是激活函數，使用ReLU函數。根據3.1.2所述，溫度對乙醇轉化率與C4烯烴選擇性的影響較為簡單，而催化劑質量與乙醇含量對兩者的影響比較復雜，不同的自變量對因變量的影響復雜度不同，因此考慮使用圖5的網絡結構，能將簡單的特征與復雜的特征結合，共同輸出給下一層網絡。

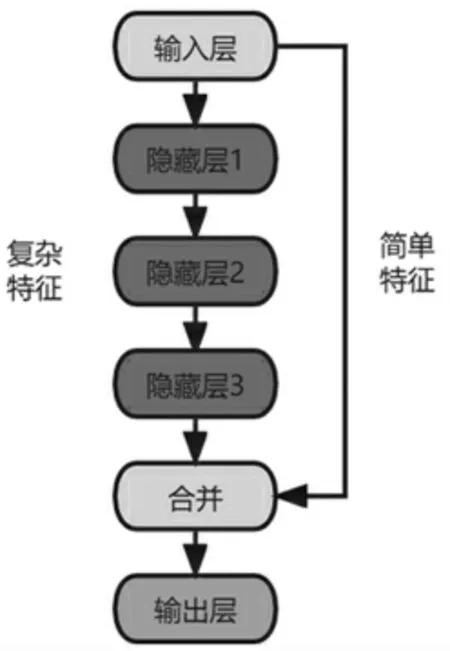
圖5 多層感知機網絡結構

2.2.2 訓練神經網絡

首先將數據集進行分割，劃分為訓練集（80%）、校驗集（10%）與測試集（10%），并對數據進行歸一化處理（均值為0，方差為1），即：

然后初始化網絡結構，設置三層隱藏層，其神經元個數初始化分別為128，100，32；輸出層神經元個數為2，即輸出乙醇轉化率與C4烯烴選擇性2個指標。損失函數選擇均方誤差，評價指標選擇決定系數，其表達式為：

同時，使用隨機梯度下降法（Stochastic Gradient Descent）訓練網絡，設置初始學習率為0.001，如果校驗集的損失函數值停滯下降的次數超過10次，學習率更新為原來的0.2倍；如果停滯次數超過20次，則結束訓練，防止模型過擬合。訓練的過程如圖6和圖7所示，經過178輪訓練，在訓練集上，loss減小到0.12，R2上升到82%。

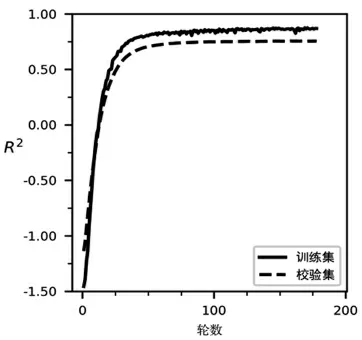
圖6 決定系數R2的訓練過程

圖7 損失函數loss的訓練過程

2.2.3 調整超參數

為了進一步提高模型的精度，需要調整初始的超參數，如學習率初始值、神經元個數。考慮到參數空間較大，本文通過k折交叉驗證，以模型在校驗集上的R2均值為評價指標，采用蒙特卡羅模擬法在一定范圍內對超參數進行搜索。參數范圍設定學習率初值在10-6～10-3，每個隱藏層神經元個數在5～200，最終得到最佳學習率為0.004 18，隱藏層神經元個數分別為172，159，127。在測試集上，模型對乙醇轉化率與C4烯烴選擇性的預測結果如圖8所示。

圖8 乙醇轉化率與C4烯烴選擇性的預測

模型在測試集上的R2=0.85，且由圖8可知，對于α、β數值較小的樣本，預測結果良好；對于α、β數值較大的樣本，預測值與真實值存在一定偏差。

2.2.4 優化生產參數

多層感知機經過優化后，能根據生產參數準確預測乙醇轉化率與C4烯烴選擇性，再通過式（2）得到C4烯烴收率。為了保證預測的合理性，需要統計出原數據各變量的最小值與最大值，確保新的生產參數應該在其范圍內。在溫度不受限時，可以建立如下的優化模型

式中：g（*）代表多層感知機的回歸函數。通過蒙特卡羅模擬法對生產參數進行反復搜索，不斷縮小搜索范圍，可以得到此時最佳生產參數，見表2。當溫度不能超過350℃時，優化模型變成

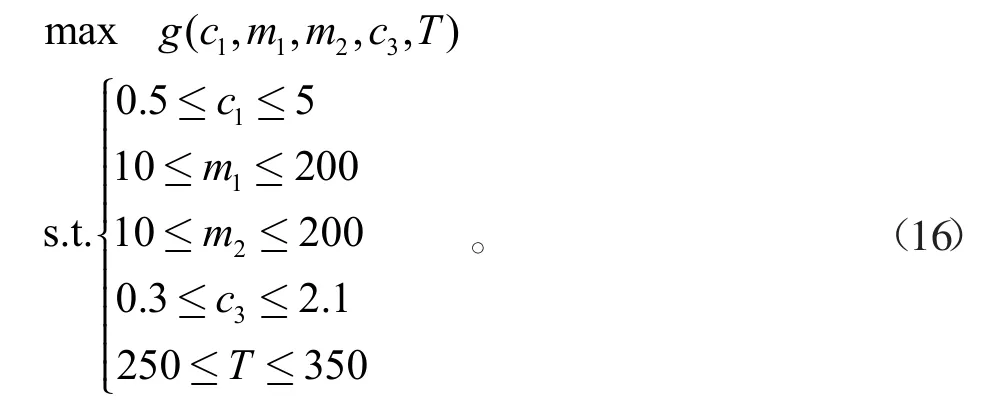
表2 溫度不受限時的最佳參數

運用同樣的方法，可得到溫度受限時的最佳參數，見表3。

表3 溫度不超過350℃時的最佳參數

其中，溫度不受限時，最優生產參數可以使乙醇轉化率達到99.03%，C4烯烴選擇性達到58.09%，最大C4烯烴收率為57.52%；溫度不超過350℃時，最優生產參數可以使乙醇轉化率達到54.33%，C4烯烴選擇性達到38.52%，最大C4烯烴收率為20.93%。并且，在2種情況下，Co/SiO2的質量、HAP的質量與溫度均會達到上界，Co負載量會在溫度不受限時達到上界，而乙醇含量會處于中間值，這說明適宜的乙醇含量才有利于C4烯烴的生成。

2.2.5 載體HAP的影響

由于模型最初刪除了催化劑組合A11，導致實驗結果全部包含載體HAP。為了分析載體對乙醇轉化率、C4烯烴選擇性的影響，讓其余參數保持不變，預測載體HAP存在時兩者的大小，結果如圖9和圖10所示。

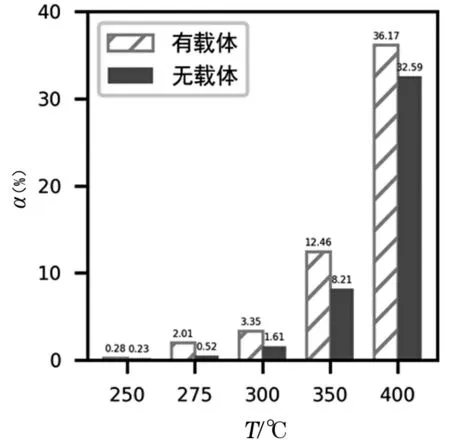
圖9 載體HAP對乙醇轉化率的影響

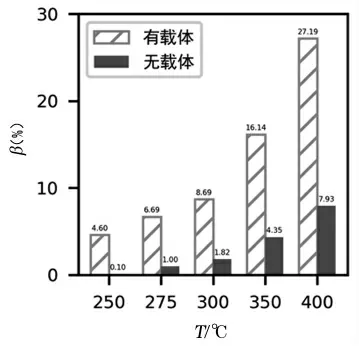
圖10 載體HAP對C4烯烴選擇性的影響

由圖9和圖10可以看到，在相同條件下，有載體HAP的轉化率與選擇性均比無載體時更大，尤其是C4烯烴選擇性，差異更加明顯。說明載體HAP能促進偶合反應，顯著提高目標產物選擇性，同時也肯定3.2.4中的含載體HAP的生產參數是最優的。

3 結論

通過嶺回歸與多層感知機模型，探索了乙醇偶合制備C4烯烴中生產參數對乙醇轉化率與C4烯烴選擇性的影響，在一定的范圍內求解出最優的生產參數，使C4烯烴收率最大。通過比較載體HAP的有無以及對比溫度不受限與受限的2種情況，發現載體HAP能提高C4烯烴選擇性以及反應溫度對生產收率有很大的影響。在實際生產中，應盡可能保持最大溫度。