求解逆特征值問題的全局性非精確牛頓類方法*
沈衛平, 王 悅
(浙江師范大學 數學與計算機科學學院,浙江 金華 321004)
0 引 言


(1)

稱c*為該逆特征值問題的解.該逆特征值問題的應用十分廣泛,如逆Strum-Liouville′s問題、逆Toeplitz eigenvalue問題、核光譜和分子光譜問題、反振弦問題等[4-16].
眾所周知,求解該逆特征值問題等價于求解如下非線性方程組問題[17-18]:
基于這種等價關系,求解一般非線性方程組的牛頓法可用于求解該逆特征值問題[19].雖然牛頓法的收斂速度是二階的,但它的每一個迭代步驟中均需要計算矩陣A(ck)的特征向量.當矩陣的規模n很大時,就需要很大的運算量.因此,文獻[19]提出了求解逆特征值問題的牛頓類方法及Cayley變換法.相較于牛頓法,這2種方法在保持二階收斂速度的同時,又避免了求解特征向量.之后,很多學者針對這2種方法的收斂性及其非精確形式進行了研究[1-2,20].除了上述提到的方法外,還有一些方法在降低運算的難度與加強算法的穩定性方面也有顯著的成效,例如文獻[3,21]中的Ulm類方法.
但這些方法僅僅具有局部收斂性,只有在解的附近選取初值才能保證迭代序列收斂.基于文獻[19]中的Cayley變換法,文獻[22]提出了一種求解逆特征值問題的全局性算法.即使初值離解很遠,該全局算法產生的迭代序列也能收斂.一個自然的問題是,能否基于文獻[1,19]中的(非精確)牛頓類方法,構造一種新的具有全局收斂性質的(非精確)牛頓類方法.
本文提出了一種用以求解逆特征值問題的全局性非精確牛頓類方法.不同于文獻[22]中的全局算法,本文的全局算法通過反冪法獲得近似特征向量,并采用經典回溯法進行全局化.在一定的條件下,給出了該全局算法的收斂性分析,并證明了它的收斂階.最后,通過數值例子驗證了該算法的全局收斂性質及其收斂階.
1 全局性非精確牛頓類方法

算法1全局性的非精確牛頓類方法

ρ(c0)=[ρ1(c0),ρ2(c0),…,ρn(c0)]T=[λ1(c0),λ2(c0),…,λn(c0)]T;
計算雅可比矩陣J(c0),其元素為
求解雅可比方程
J(c0)c1=λ*.
(2)
2)對于k=1,2,…直到ck收斂,具體步驟如下:
①非精確求解方程
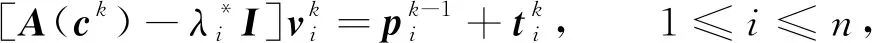
(3)


(4)

且令ρ(ck)=[ρ1(ck),ρ2(ck),…,ρn(ck)]T.
④計算近似雅可比矩陣Jk,其元素為
⑤非精確求解雅可比方程

(5)

其中,

(6)
⑦若

(7)

⑧計算下一個迭代點:ck+1=ck+Δck.
注1本文提出的算法與文獻[22]中的算法的最大區別在于得到近似特征向量的方式不同.本文的算法利用反冪法得到近似特征向量,而文獻[22]的算法則是基于Cayley變換求得近似特征向量.
2 收斂性分析

[J(c)]ij=(qi(c))TAjqi(c), 1≤i,j≤n.
需要引進下面幾個引理.其中,引理1的證明可參閱文獻[23]中的定理4.7;引理2及引理3的證明分別類似于文獻[22]中的引理4及引理6;引理4及引理5的證明分別類似于文獻[1]中的引理4.1及引理4.2.為了節省篇幅,將其證明省略.
引理1[23]任意ε>0,存在充分小的正數δ0,對任意k∈N,當‖Δck‖≤δ0時,
‖ρ(ck+Δck)-ρ(ck)-JkΔck‖≤ε‖Δck‖.

‖ρ(ck)-λ*+JkΔck‖≤ηk‖ρ(ck)-λ*‖;
(8)
‖ρ(ck+Δck)-λ*‖≤(1-t(1-ηk))‖ρ(ck)-λ*‖.
(9)
引理3[22]假設k∈N且近似雅可比矩陣Jk可逆,則
‖Δck‖≤τk(1-ηk)‖ρ(ck)-λ*‖.
(10)
引理4[1]設k∈N且設γ為任意正數.若
則
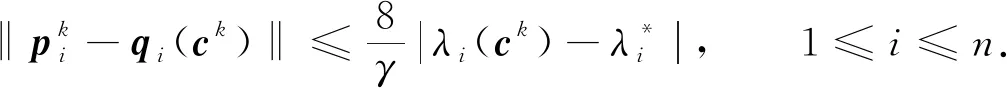
(11)
引理5[1]存在正數δ1,ξ0與γ,對任意k∈N,當‖ck-c*‖≤δ1時,下列式子成立:

(12)
‖qi(ck)-qi(c*)‖≤ξ0‖ck-c*‖, 1≤i≤n;
(13)

(14)
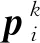
命題1設K1為任意正整數,則存在正數δ2及ξ(不依賴于K1),若

(15)
且
‖ck-c*‖≤δ2, ?k≥K1,
(16)
則對任意k≥K1,式(12)、式(14)及下面2個式子成立:

(17)

(18)
證明設正數ξ0,γ及δ1為引理5中的常數.令

(19)
下證ξ及δ2即為滿足命題1結論的常數.為此,假設式(15)及式(16)成立.由式(16)及δ2的定義,并利用引理5可知,對任意k≥K1,式(12)~式(14)均成立.接下來利用數學歸納法證明對任意k≥K1,式(17)與式(18)成立.為簡便起見,設1≤i≤n.顯然,由式(15)知,當k=K1時,式(17)成立.根據范數的三角不等式,有

(20)
于是,結合式(15)和式(13)(k=K1+1)可得
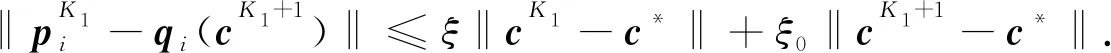
(21)
進一步,再利用式(16)和δ2的定義,容易推得
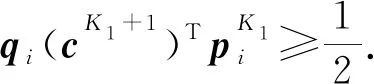
從而,當k=K1時,式(18)成立.
假設當k≤l-1時,式(17)及式(18)成立.于是,應用引理4并結合式(12)(k=l),有

(22)
因此,結合式(13)及ξ的定義,可得
也就是說,當k=l時,式(17)成立.注意到當k=l時,式(18)的證明完全類似于其k=K1時的證明,考慮到篇幅問題,筆者省略了這部分的證明.于是,命題1得證.
為了證明全局性非精確牛頓類方法的全局收斂性和收斂階,需要引入下面3個引理.其中,引理6的證明可以參閱文獻[1]中的引理4.4;引理7及引理8 的證明可以分別參閱文獻[22]中的推論7和引理9.
引理6[1]對任意k∈N,由算法1產生的近似雅可比矩陣Jk滿足

(23)
引理7[22]設k∈N.若ρ(ck)-λ*≠0且近似雅可比矩陣Jk可逆,則當算法1中步驟⑦的內循環停止時,
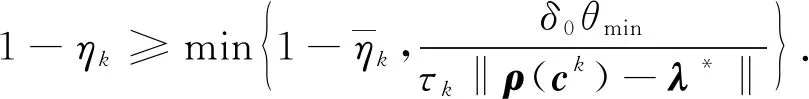
(24)



(25)
下面給出本文的主要定理.


(26)
則當k→∞時,ck→c*且ρ(ck)→λ*,并且序列{ck}至少具有β階的收斂速度.
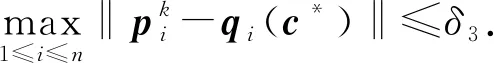
下面利用反證法證明序列{ck}的收斂性.假設當k→∞時,ck→/c*,則存在δ5∈(0,δ4)和子列{ckt},使得ckt?B(c*,δ5),t=1,2,….又因為c*是序列{ck}的聚點,故存在序列{kj}?N,使得當j→∞時,ckj→c*.選擇lj>0滿足kj+lj 結合式(25)可知,對任意的k≥K2, (27) 又因為ck+1=ck+Δck,所以存在充分大的正整數K3≥K2,對任意的j≥K3,有 (28) 其中倒數第2個不等式可由引理3推得.由式(9)易得 因此, (29) 另一方面,因為t,ηk∈(0,1),所以由式(9)可知 ‖ρ(ck+1)-λ*‖≤‖ρ(ck)-λ*‖, ?k∈N. 因此, (30) 于是,結合式(28)~式(30),有 (31) 又因為當j→∞時,有ckj→c*,所以,‖ρ(ckj)-λ*‖-‖ρ(ckj+1)-λ*‖→0,得到矛盾.因此,假設不成立.從而,當k→∞時,ck→c*. 接下來證明當k→∞時,ρ(ck)→λ*.由定理1條件并應用命題1可得,對任意k≥K2,式(12)、式(14)、式(17)及式(18)成立.于是,應用引理4,當k≥K2+1時, (32) 因為 (33) 因此,利用式(12)、式(32)及式(33),對任意k≥K2+1, (34) 又因為 (35) 因此,由式(34)和式(35)可推出 ‖ρ(ck)-λ*‖≤ρ‖ck-c*‖, ?k≥K2+1. (36) rk=JkΔck+ρ(ck)-λ*. (37) 那么,根據算法1中的步驟⑤可知 (38) 注意到Δck=ck+1-ck和Jkck=ρ(ck).將這2個式子代入式(37),計算可得 Jk(ck+1-c*)=rk-(Jkc*-λ*). (39) ‖ck+1-c*‖≤2‖J(c*)-1‖(‖rk‖+‖Jkc*-λ*‖). (40) 應用引理6,并結合式(17)及條件ck∈B(c*,δ4),有 (41) 另一方面,利用式(38)、式(6)和式(36),容易推得 (42) 將式(41)與式(42)代入式(40),可得 從而,序列{ck}的收斂速度至少是β階的.定理1證畢. 下面將通過若干個數值例子驗證全局性非精確牛頓類方法的理論結果.例1研究了逆Toeplitz 特征值問題[16],例2考慮了Toeplitz-plus-Hankel逆特征值問題[7]. 所有的數值實驗均采用Matlab中的qmr函數求解算法1中的式(2)、式(3)及式(5).另外,當 給定的精確解與精確特征值向量分別為 c*=(2,3,4,5,6)T,λ*=(-5.236 1,-1.587 6,-0.763 9,-0.555 5,18.143 1)T. 例1考慮以下3個不同的初始值:1)c0=(1,2,3,4,5)T;2)c0=(21,38,46,63,81)T;3)c0=(150,159,168,170,180)T.表1~表3列出了在這3個初始值下,該全局算法的數值實驗結果. 表1 初值為c0=(1,2,3,4,5)T的數值實驗結果 表2 初值為c0=(21,38,46,63,81)T的數值實驗結果 表3 初值為c0=(150,159,168,170,180)T的數值實驗結果 給定的精確解與精確特征值分別為: c*=(15,16,17,18,19)T,λ*=(-59.951 4,-24.048 5,-19.696 4,23.258 6,53.437 7)T. 考慮以下3個不同的初始值:1)c0=(31,32,33,34,35)T;2)c0=(35,45,60,80,95)T;3)c0=(150,159,168,175,185)T.表4~表6列出了在這3個初始值下,該全局算法的數值實驗結果. 表4 初值為c0=(31,32,33,34,35)T的數值實驗結果 表5 初值為c0=(35,45,60,80,95)T的數值實驗結果 表6 初值為c0=(150,159,168,175,185)T的數值實驗結果 從上面2個例子的數值實驗結果可以看出,即使初始值沒有靠近問題的解c*,由算法1產生的序列{ck}依然能收斂至c*,這恰好說明了本文所提出的非精確牛頓類算法的收斂性具有全局性質.同時,從表1~表6中的數據也可以看出序列{ck}的超線性收斂性質.


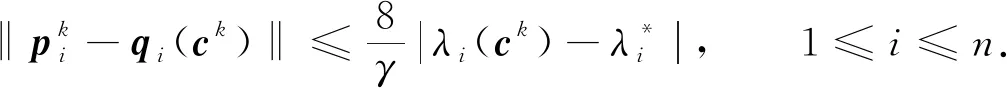
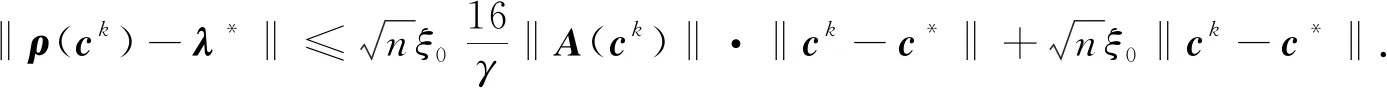





3 數值算例









