泛函微分方程分析與設計中幾類關鍵問題研究成果

云南民族大學數(shù)學與計算機科學學院

1 創(chuàng)新點

項目研究突破了現(xiàn)有研究方法的局限性，降低了現(xiàn)有研究結論的保守性，為泛函微分方程的分析與設計提供了新的理論分析方法。主要創(chuàng)新點如下：

1.1 李雅普諾夫泛函的合理構造

項目針對不同類型的泛函微分方程，根據(jù)方程的結構特點及其分析與設計要求，提出了幾類新的李雅普諾夫泛函構造方法。具體如下：

一是Markov跳躍參數(shù)依賴的積分二次型李雅普諾夫泛函的構造方法。

本項目提出了Markov跳躍參數(shù)依賴的積分二次型李雅普諾夫泛函的構造方法。該方法中的正定矩陣依賴于方程參數(shù)的跳躍模態(tài)，不僅增加了矩陣變量的靈活度，而且降低了系統(tǒng)分析結果的保守性。

二是高階采樣時刻依賴型李雅普諾夫泛函的構造方法。

項目利用自由矩陣零等式和輸入時滯的特性，建立了高階采樣時刻依賴型李雅普諾夫泛函的構造方法。該方法蘊含較多的采樣時刻信息，克服了傳統(tǒng)李雅普諾夫泛函因僅含一階采樣時刻信息帶來的局限性，降低了現(xiàn)有分析與設計結果的保守性。

1.2 參數(shù)依賴型矩陣系數(shù)多項式的定性判別方法

項目基于矩陣分析理論和凸優(yōu)化理論，結合參數(shù)依賴型矩陣系數(shù)多項式的結構特點，建立了參數(shù)依賴型矩陣系數(shù)多項式的定性判別方法。該方法克服了現(xiàn)有方法因難以獲得矩陣系數(shù)多項式的定性判據(jù)而導致的難以獲得理想的分析與設計結論的局限性，降低了現(xiàn)有分析與設計結果的保守性。

1.3 不等式的改進與應用

一是非正交多項式依賴型自由矩陣積分不等式。

項目基于泛函分析理論和矩陣分析理論，結合非正交多項式的積分特點，借助自由矩陣思想，建立了基于非正交多項式的自由矩陣積分不等式。該不等式降低了因正交多項式本身具有的局限性而導致所得結果存在的保守性。

二是參數(shù)依賴型廣義互凸組合不等式。

本項目基于矩陣分析理論和凸優(yōu)化理論，結合互凸參數(shù)的結構特點，利用參數(shù)變換方法和其他分析技巧，建立了參數(shù)依賴型廣義互凸組合不等式。該不等式解決了現(xiàn)有互凸組合不等式難以估計n階互凸組合二次項的界值，從而導致蘊含異質時滯因素的泛函微分方程的分析與設計受到阻礙的重大問題。

2 成果應用情況

1）基于項目研究建立的參數(shù)依賴型矩陣系數(shù)多項式的定性判別方法，代表作[3]獲得了新的時滯依賴穩(wěn)定性判據(jù)。數(shù)值仿真結果（見表1）表明，基于本方法獲得的系統(tǒng)穩(wěn)定性判據(jù)（定理3.1）可允許的時滯最大可行上界遠大于其他方法可允許的時滯上界，從而說明本項目提出的方法在降低理論結果保守性方面具有重要作用。

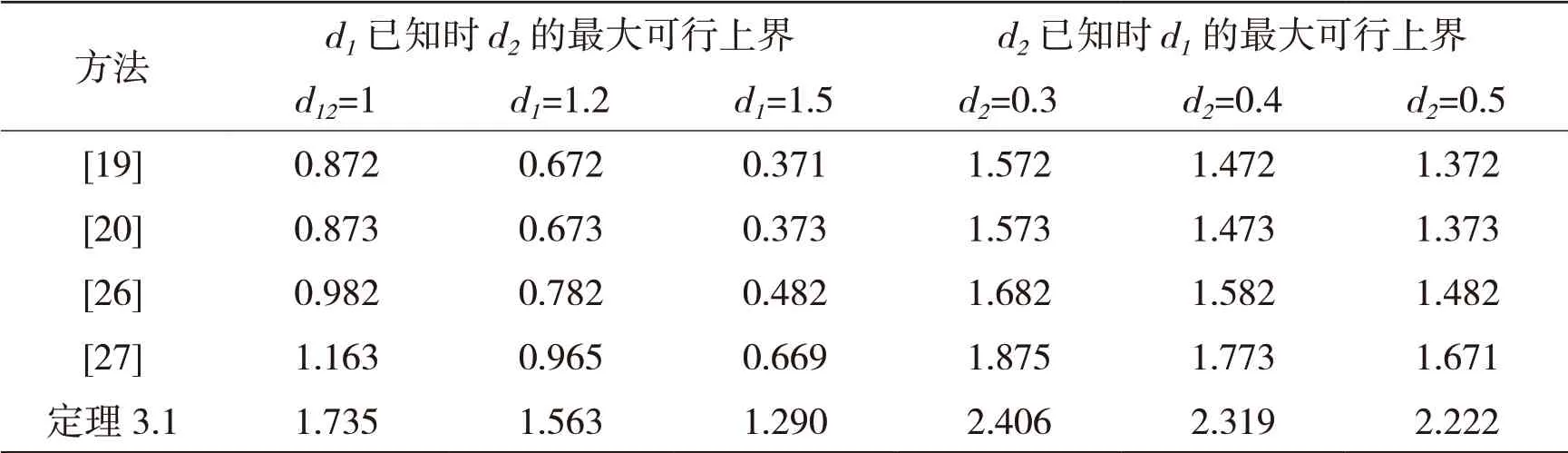
表1 不同方法允許的加性時滯最大可行上界

2）基于項目研究建立的非正交多項式依賴型自由矩陣積分不等式，代表作[13]獲得了新的穩(wěn)定性判據(jù)和擴展耗散條件。數(shù)值仿真結果（見表2）表明，基于非正交多項式依賴型自由矩陣積分不等式獲得的系統(tǒng)穩(wěn)定性判據(jù)（推論1）可允許的時滯最大可行上界不僅優(yōu)于已有的結論，幾乎可以達到該系統(tǒng)可允許的時滯上界的解析值，從而說明該不等式在降低理論結果保守性方面具有重要作用。

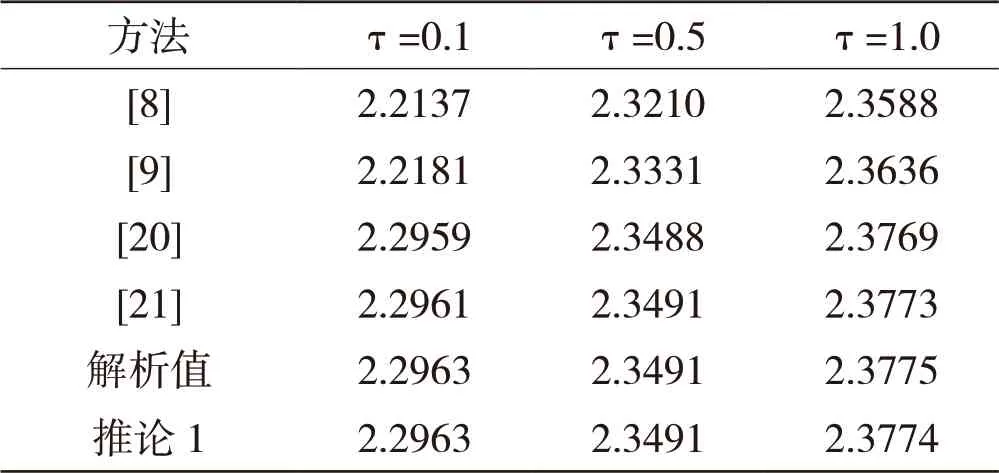
表2 τ已知時h的最大可行上界

3）基于項目研究提出的Markov跳變參數(shù)依賴的積分二次型李雅普諾夫泛函的構造方法，代表作[4]獲得了新的穩(wěn)定性判據(jù)和控制器設計方案。數(shù)值仿真結果（見圖1和圖2）表明，當系統(tǒng)沒有控制輸入時，系統(tǒng)是發(fā)散的，而采用本項目設計的控制方案時，系統(tǒng)的狀態(tài)可以實現(xiàn)漸近穩(wěn)定，從而說明本項目提出的方法是切實可行的。

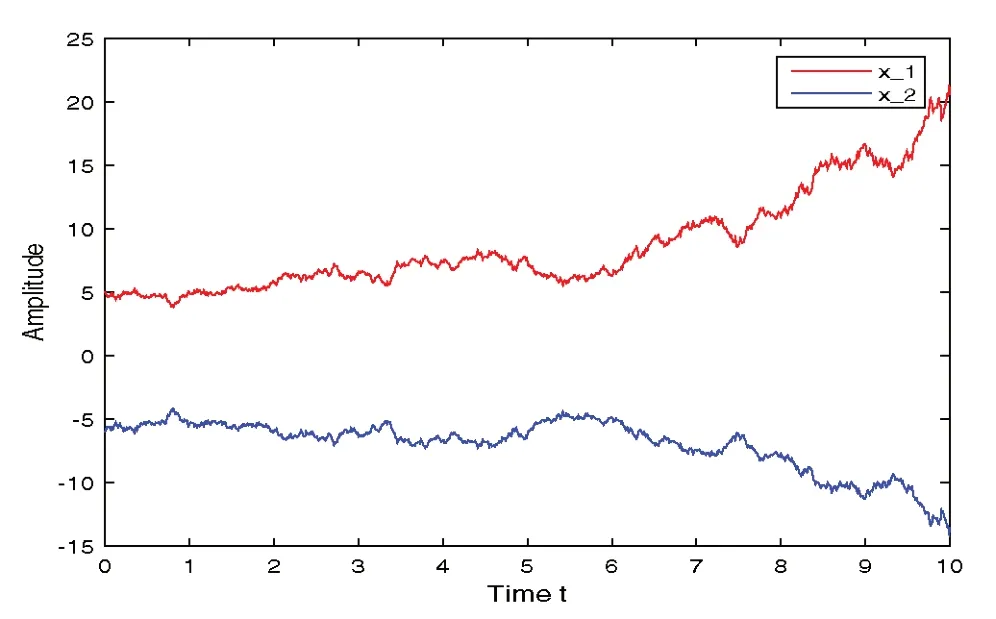
圖1 無控制輸入時，系統(tǒng)的狀態(tài)響應

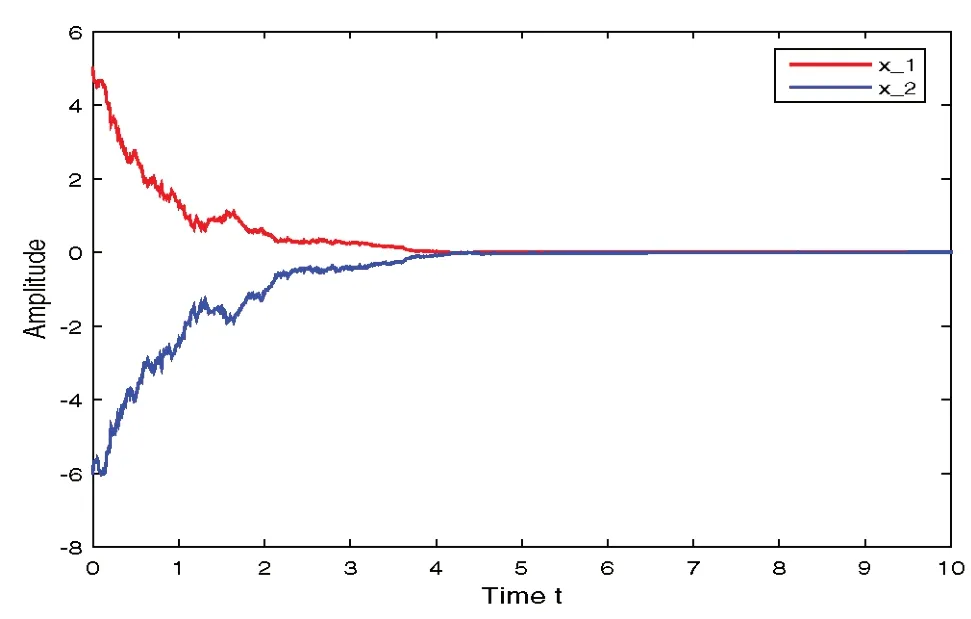
圖2 有控制輸入時，系統(tǒng)的狀態(tài)響

4）基于項目研究提出的高階采樣時刻依賴型李雅普諾夫泛函構造方法，代表作[1]獲得了新的系統(tǒng)鎮(zhèn)定性判定條件和模糊采樣控制方案。數(shù)值仿真結果（見表3、圖3、圖4和圖5）表明，基于該方法獲得的系統(tǒng)鎮(zhèn)定性判據(jù)（推論1）可允許的最大采樣間隔優(yōu)于現(xiàn)有結論所允許的最大采樣間隔。不僅如此，由圖3、圖4和圖5不難發(fā)現(xiàn)，基于該方法設計的模糊采樣控制器可以非常有效地鎮(zhèn)定具有半Markov跳躍的混沌系統(tǒng)。

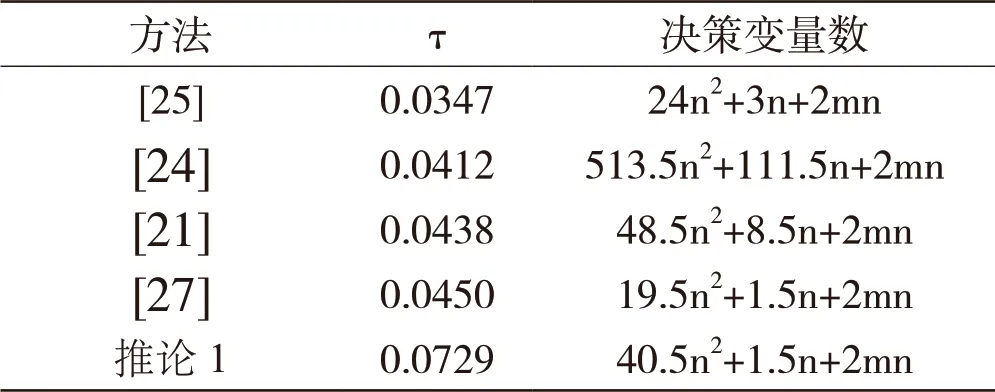
表3 不同方法允許的最大采樣間隔τ

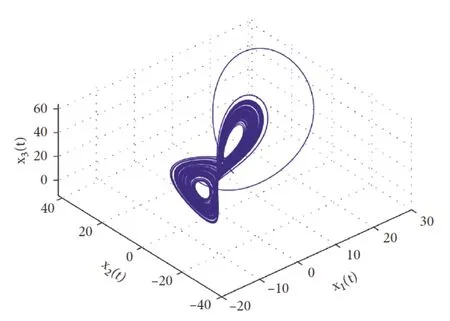
圖3 無控制輸入時，系統(tǒng)的狀態(tài)響應

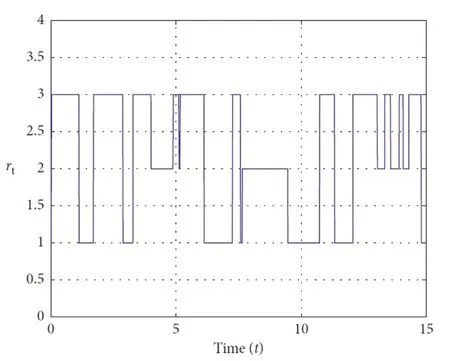
圖4 半Markov過程的跳躍模態(tài)

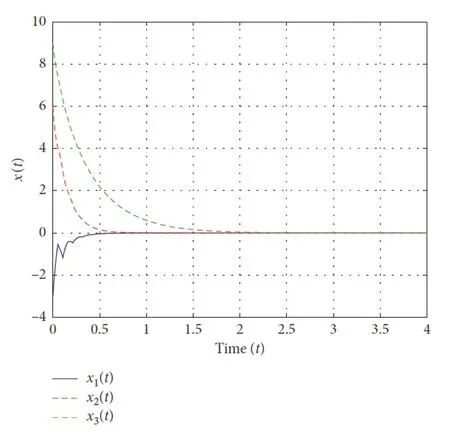
圖5 有控制輸入時，系統(tǒng)的狀態(tài)響應

5）基于項目研究提出的參數(shù)依賴型廣義互凸組合不等式，代表作[2]研究了轉移速率部分未知的半Markov跳躍中立型泛函微分方程的隨機穩(wěn)定性問題；代表作[12]研究了具有加性時滯的Markov跳躍泛函微分方程的隨機穩(wěn)定性問題；代表作[18]研究了不確定中立型半Markov跳躍泛函微分方程的隨機有限時間魯棒有界性問題。數(shù)值仿真（見表4、圖6和圖7）表明，基于該方法建立的分析與設計結果具有更低的保守性。

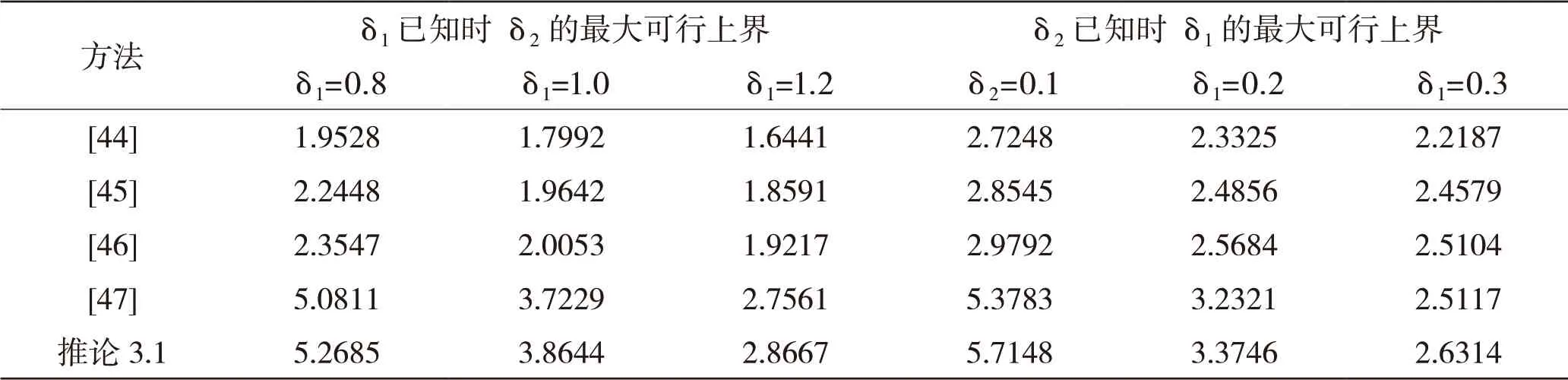
表4 不同方法允許的加性時滯最大可行上界

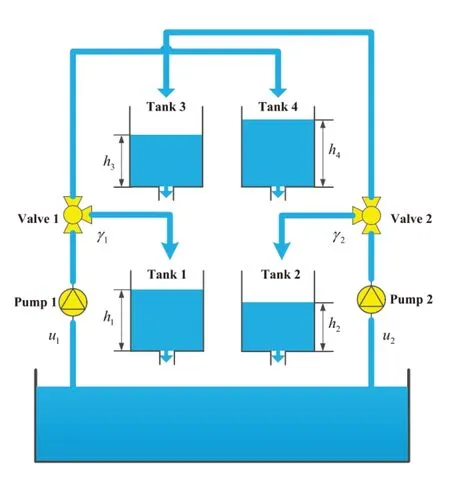
圖6 四槽反應系統(tǒng)結構圖

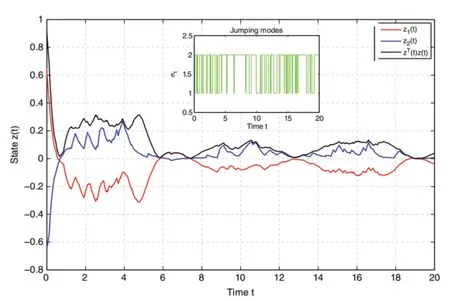
圖7 系統(tǒng)狀態(tài)隨機有限時間有界