基于一維卷積神經(jīng)網(wǎng)絡(luò)的高分辨率Radon變換反演方法研究

薛亞茹，郭蒙軍*，馮璐瑜，馬繼濤，陳小宏

1 中國石油大學(xué)(北京)信息科學(xué)與工程學(xué)院，北京 102249 2 中國石油大學(xué)(北京)地球物理學(xué)院，北京 102249

0 引言

地震勘探包括地震數(shù)據(jù)采集、處理和解釋三個主要環(huán)節(jié)，其中數(shù)據(jù)處理通過各種數(shù)學(xué)、物理等方法處理采集到的地震數(shù)據(jù)，為之后的地震資料解釋提供高質(zhì)量數(shù)據(jù)支撐(楊子鵬等，2021；鄭迎冬等，2021).Radon變換是地震數(shù)據(jù)常用處理方法之一，最早由Claerbout和Johnson(1971)引入地震勘探領(lǐng)域，之后被廣泛應(yīng)用于多次波壓制(Zhang and Wang,2006;Kazemi and Sacchi,2021)、缺失地震道重建(王維紅等，2007；唐歡歡等，2020)和波場分離(曾有良等，2007; 朱翔宇等，2018)等工作中.

Radon變換的基本原理是將不同曲率的同相軸映射到Radon域參數(shù)，以實現(xiàn)同相軸特征識別.但由于地震數(shù)據(jù)采集系統(tǒng)是有限的離散空間，導(dǎo)致同一同相軸會映射Radon域的多個參數(shù)，引起分辨率降低；同時由于Radon變換是非正交變換，導(dǎo)致其無法保留數(shù)據(jù)真振幅.針對上述問題，學(xué)者們展開了Radon變換反演方法研究.Thorson 和 Claerbout(1985)提出基于最大后驗概率(Maximum A Posteriori, MAP)的隨機反演思想，改善了Radon變換分辨率，該方法在時域?qū)崿F(xiàn)Radon反演，反演矩陣維度大，計算量大.對于動校正后的地震剖面，Hampson(1986)提出了頻率域拋物Radon變換，不同頻率反演解耦，大大提高了計算效率，但該方法采用最小二乘反演，得到的Radon變換參數(shù)光滑，分辨率較低.為提高Radon變換分辨率，Sacchi和Ulrych(1995)提出基于貝葉斯原理的反演理論，將模型的先驗信息作為正則化約束稀疏反演，得到了頻域高分辨率Radon變換.在此基礎(chǔ)上，Sacchi和Porsani(1999)利用共軛梯度和循環(huán)矩陣提高了高分辨率Radon變換處理大型數(shù)據(jù)時的計算速度.為進一步提高計算效率，有學(xué)者提出頻率約束的思想，即選擇一個主要頻率分量，以此頻率分量來約束其他所有頻率，避免因迭代過程中矩陣求逆導(dǎo)致計算量大的問題(Herrmann et al.,2000;Chen and Lu,2011；劉仕友等，2019).

頻率域Radon反演方法雖然有效提高了計算效率，但對時域沒有稀疏約束.Cary(1998)指出時域算法可以實現(xiàn)時間和Radon參數(shù)兩者的稀疏性，分辨率進一步提升，但是計算速度相比于頻域算法較慢；之后Trad等(2003)結(jié)合了Radon變換時域的稀疏性以及頻域的計算高效性，實現(xiàn)了混合域Radon變換；熊登等(2009)為頻域拋物Radon變換引入時變稀疏權(quán)，在混合域?qū)崿F(xiàn)了高分辨率拋物Radon變換，并用于多次波衰減；隨后Lu(2013)在混合域求解過程中引入了迭代收縮算法，進一步提高了混合域Radon變換的計算效率；考慮地震數(shù)據(jù)受非高斯噪聲分布影響，Wang等(2019)提出時域雙L1范數(shù)稀疏約束的魯棒時不變Radon變換，并引入交替分割Bregman算法來提高Radon模型計算效率.對于雙曲Radon變換時域求解效率低下的問題，Hu等(2013)通過構(gòu)造雙曲Radon算子的低秩近似和蝴蝶結(jié)構(gòu)，提出一種快速求解雙曲Radon變換的蝴蝶算法，實現(xiàn)了單個積分算子的快速求解；面對速度各向異性發(fā)育介質(zhì)及長偏移距情況下的地震數(shù)據(jù)，鞏向博等(2014)提出各向異性Radon變換，改善了復(fù)雜地質(zhì)條件下Radon域能量不收斂的問題，并利用最優(yōu)相似系數(shù)加權(quán)Gauss-Seidel迭代算法，具有較高的時域計算效率；Gholami和Farshad(2019)通過延時間軸插值拉伸數(shù)據(jù)，并用基于快速傅里葉變換的chrip-z變換快速計算新坐標(biāo)系下的求和路徑，得到一種快速計算雙曲Radon變換及其稀疏計算的方法.

上述學(xué)者從不同角度解決Radon變換面臨的計算效率和反演分辨率問題.由于Radon變換空間是不同曲率的時距曲線，其分辨率越高，Radon反演基函數(shù)相關(guān)性越強，反演矩陣病態(tài)性越強，目前的線性反演方法難度越大，因此有待于提出新的反演思路改進Radon變換.

近幾年，人工智能和深度學(xué)習(xí)在計算機視覺和圖像領(lǐng)域快速發(fā)展，對于反問題求解，Gregor和LeCun(2010)在稀疏編碼背景下提出學(xué)習(xí)型的迭代軟閾值算法，通過訓(xùn)練具有特定結(jié)構(gòu)和固定深度的非線性前饋預(yù)測器，學(xué)習(xí)傳統(tǒng)迭代軟閾值算法的兩個矩陣，以此得到稀疏編碼的最佳近似，提高了稀疏編碼的效率，此后，有關(guān)逆問題求解的深度學(xué)習(xí)方法不斷涌現(xiàn).Yang等(2016)將傳統(tǒng)的交替方向乘子法與神經(jīng)網(wǎng)絡(luò)相結(jié)合，用來重建磁共振圖像，網(wǎng)絡(luò)以端到端的方式進行訓(xùn)練，網(wǎng)絡(luò)架構(gòu)結(jié)合了傳統(tǒng)的交替方向乘子算法，增強了網(wǎng)絡(luò)的可解釋性；除此之外，Borgerding等(2017)通過展開傳統(tǒng)的近似消息傳遞算法，提出了基于近似消息傳遞算法的用于求解線性逆問題的深度神經(jīng)網(wǎng)絡(luò).為解釋深度學(xué)習(xí)框架適用于圖像特定反問題求解的合理性，Ye等(2018)提出一種通用的求解反問題的深度卷積框架神經(jīng)網(wǎng)絡(luò)(Deep Convolutional Framelets Neural Network, DCFNN)，表明深度神經(jīng)網(wǎng)絡(luò)中的殘差塊、級聯(lián)ReLU函數(shù)和冗余濾波通道有助于實現(xiàn)逆問題求解，揭示了現(xiàn)有求解逆問題深度學(xué)習(xí)網(wǎng)絡(luò)架構(gòu)的局限性.對于欠采樣磁共振圖像重建這一不適定線性反演問題，Mardani等(2019)提出一種基于生成對抗網(wǎng)絡(luò)(Generative Adversarial Network, GAN)的壓縮感知方法，其中生成器為一個帶有跳躍連接的深度殘差網(wǎng)絡(luò)，用來消除混疊偽影，判別器為一個多層卷積神經(jīng)網(wǎng)絡(luò)，用來評判映射后的圖像質(zhì)量.有別于展開迭代優(yōu)化算法的神經(jīng)網(wǎng)絡(luò)，Gilton等(2019)通過截斷Neumann級數(shù)，提出一個求解逆問題的端到端，數(shù)據(jù)驅(qū)動的Neumann網(wǎng)絡(luò)，在標(biāo)準(zhǔn)數(shù)據(jù)集上的效果要優(yōu)于展開的迭代方法.Ongie等(2020)總結(jié)了近些年深度學(xué)習(xí)在求解圖像逆問題領(lǐng)域的應(yīng)用，并根據(jù)前向模型是否已知以及網(wǎng)絡(luò)是否為監(jiān)督或無監(jiān)督學(xué)習(xí)對其進行了分類.

深度學(xué)習(xí)的發(fā)展也促進了Radon變換反演問題的研究.Kaur等(2020a)通過建立CycleGAN網(wǎng)絡(luò)來近似逆Hessian矩陣，得到與傳統(tǒng)迭代反演類似的效果，且計算量相較于傳統(tǒng)算法有所下降；之后，Kaur等(2020b)將CycleGAN網(wǎng)絡(luò)學(xué)習(xí)逆Hessian矩陣的方法用于求解雙曲Radon變換，在降低計算量的同時達到了與傳統(tǒng)最小二乘法相同的結(jié)果.上述GAN網(wǎng)絡(luò)需要生成器和判別器協(xié)同完成逆Hessian矩陣的學(xué)習(xí)，網(wǎng)絡(luò)結(jié)構(gòu)較復(fù)雜.本文結(jié)合Radon變換的卷積模型，通過建立簡單的一維卷積網(wǎng)絡(luò)模型，借助于卷積神經(jīng)網(wǎng)絡(luò)的非線性表征能力，實現(xiàn)高分辨率Radon變換反演；具體分析串、并聯(lián)兩種模型神經(jīng)網(wǎng)絡(luò)的工作機理，與傳統(tǒng)高分辨率Radon變換反演方法進行對比，驗證本文提出的卷積神經(jīng)網(wǎng)絡(luò)實現(xiàn)高分辨率Radon變換的可行性及有效性.

1 Radon變換基本原理

地震數(shù)據(jù)處理中常用的Radon變換有線性Radon變換、拋物Radon變換和雙曲Radon變換，其中線性Radon變換和拋物Radon變換具有時不變性，可通過Fourier變換從時間-空間域變換到頻率-空間域，實現(xiàn)不同頻率數(shù)據(jù)解耦，降低反演矩陣維度.以拋物Radon變換為例，地震數(shù)據(jù)可以表示為沿不同曲率拋物路徑的同相軸疊加，即：

(1)

其中t為時間，τ為時空域雙重走時截距，q為曲率參數(shù)，h為偏移距，Nq為Radon域中曲率參數(shù)個數(shù).

將式(1)變換到頻域，有：

(2)

式中e-iω qjh2表示頻率為ω，曲率為qj的同相軸，其相位隨偏移距h的增加而增加.由于拋物Radon變換可以用上述簡單的相移參數(shù)表示同相軸的隨偏移距的展布，而且不同頻率之間相互獨立，因此拋物Radon變換可以分頻處理.對某一頻率分量，將上述相移算子用矩陣表示：

(3)

式中Nh為道數(shù)，每一列表示了不同曲率參數(shù)的Radon變換基函數(shù).Radon變換表示為矩陣形式：

d=Lm,

(4)

其中d表示某一頻率分量的地震向量，m為其對應(yīng)頻率分量的Radon參數(shù)向量.對式(4)轉(zhuǎn)置運算，可得到Radon共軛解：

mH=LHd.

(5)

將式(4)代入式(5)，可得到共軛解與真實Radon參數(shù)之間的關(guān)系：

mH=LHd=LHLm.

(6)

由于Radon變換算子L是非正交的，所以LHL不是單位矩陣，也就表明Radon共軛解mH并不是真實的Radon參數(shù).又因Radon算子L被限制在有限偏移距范圍內(nèi)，使得同相軸無法聚焦到一個理想的Radon曲率參數(shù)，從而產(chǎn)生擴散，且采集范圍越小，擴散越嚴(yán)重.

為克服Radon變換的非正交性，通常采用最小二乘法降低重構(gòu)數(shù)據(jù)與真實數(shù)據(jù)之間的誤差，定義優(yōu)化函數(shù)為：

由式(7)可得到Radon變換最小二乘解為：

m=(LHL)-1LHd.

(8)

上述Hessian矩陣求逆不穩(wěn)定，且分辨率低.Sacchi和Ulrych(1995)提出基于Bayes理論的隨機反演方法.該方法將模型的先驗信息引入反演過程，形成正則化目標(biāo)函數(shù)：

(9)

其中Wm是對參數(shù)的正則化約束，μ為阻尼因子.當(dāng)Wm為單位矩陣時，正則項與先驗參數(shù)沒有關(guān)系，僅引入阻尼因子，實現(xiàn)對參數(shù)的光滑約束，分辨率不高；當(dāng)假設(shè)Radon參數(shù)服從Cauchy分布時，Wm為Radon參數(shù)的協(xié)方差對角矩陣，即Wii=1/(|mi|2+b2)；當(dāng)采用L1范數(shù)正則化約束，Wii=1/(|mi|+b2)，其中b都是一個較小的數(shù)，避免分母為零.

上述正則化方法是目前Radon變換反演的主要方法，通常采用迭代求解方法，例如迭代加權(quán)最小二乘法(Iterative Reweighted Least Square, IRLS)，迭代收縮閾值法(Iterative Shrinkage Threshold Algorithm, ISTA)等，在這些方法中都無法避免Hessian矩陣求逆帶來計算量大的問題；同時對于迭代優(yōu)化方法，在使用過程中權(quán)重系數(shù)μ的選取，迭代次數(shù)等超參數(shù)都需要進行調(diào)整優(yōu)化，影響數(shù)據(jù)處理質(zhì)量.

2 基于褶積模型的Radon變換反演

2.1 Radon變換的褶積模型

Radon變換反演通常采用數(shù)據(jù)d與參數(shù)m之間的反演映射關(guān)系，算子L是非正交矩陣，且不同曲率參數(shù)的Radon變換基函數(shù)相關(guān)性較大，帶來矩陣求逆的不穩(wěn)定性、矩陣求逆計算量大等問題.觀察式(6)，它建立了Radon共軛解與真實解之間的映射關(guān)系，其中映射算子是Radon算子的自相關(guān)矩陣，構(gòu)成了一個共軛對稱的Hessian矩陣.定義該矩陣為Φ=LHL，具體形式為：

(10)

(11)

其中*表示褶積運算，褶積核函數(shù)由Φ矩陣的第一列和第一行構(gòu)成，mqi為不同曲率對應(yīng)的Radon參數(shù).圖1a所示為30 Hz的褶積核，該褶積核函數(shù)對真實Radon參數(shù)的褶積形成了一個低通濾波作用，因此可被描述為一個模糊褶積算子(Hu et al., 2001).

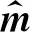
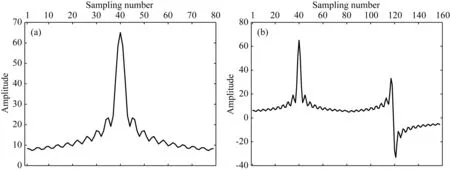
圖1 褶積核數(shù)據(jù)(a) 幅度； (b) 實部和虛部串接.Fig.1 Convoluted kernel data(a) Amplitude； (b) Concatenation of real and imaginary part.

神經(jīng)網(wǎng)絡(luò)通常處理實數(shù)數(shù)據(jù)，對于復(fù)數(shù)數(shù)據(jù)，本文采用將復(fù)數(shù)實部與虛部串聯(lián)構(gòu)成實數(shù)序列，圖1b為褶積核的實部和虛部的串接，構(gòu)成了一個更為復(fù)雜的褶積核函數(shù).

2.2 基于反褶積原理的串聯(lián)反演模型

根據(jù)式(11)建立的褶積模型，可以設(shè)計反褶積濾波器，實現(xiàn)高分辨率Radon變換反演.基本原理如圖2所示，與褶積核形成串聯(lián)模型關(guān)系.

圖2 反褶積濾波器Fig.2 Deconvolution filter

由圖2可以得到串聯(lián)神經(jīng)網(wǎng)絡(luò)模型F1與褶積核函數(shù)關(guān)系為：

F1=CNN(Φ)=Φ-1，(12)

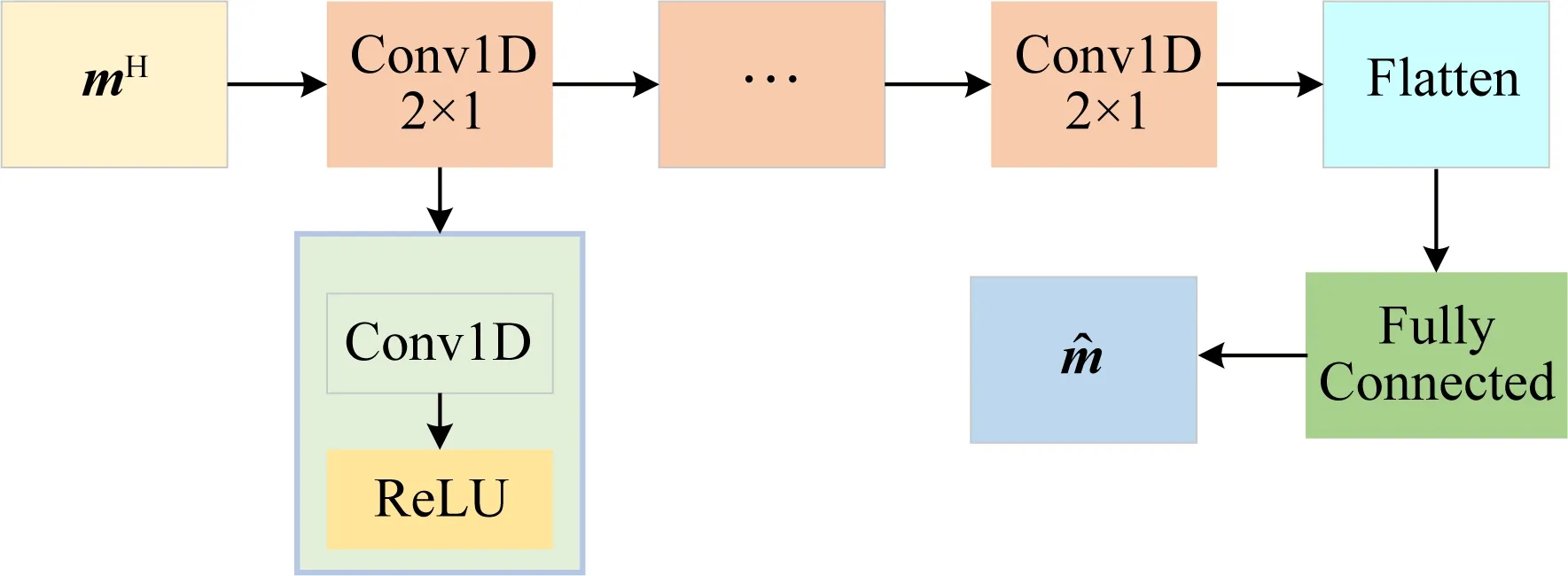
圖3 串聯(lián)型一維卷積網(wǎng)絡(luò)Fig.3 Serial 1-D CNN

式中CNN為建立的串聯(lián)型一維卷積網(wǎng)絡(luò)，用來學(xué)習(xí)Radon變換反褶積算子，實現(xiàn)低分辨率解到高分辨率解的映射.本文串聯(lián)型一維卷積網(wǎng)絡(luò)結(jié)構(gòu)如圖3所示，包含卷積層、展平層和全連接層，其中每個卷積層都包含一個一維卷積過程和一個ReLU激活函數(shù)，其中一維卷積用來學(xué)習(xí)數(shù)據(jù)特征，ReLU激活函數(shù)為網(wǎng)絡(luò)提供非線性變換，卷積層的個數(shù)可根據(jù)數(shù)據(jù)復(fù)雜度進行調(diào)整；展平層用來將多維數(shù)據(jù)轉(zhuǎn)化為一維數(shù)據(jù)，以進行后續(xù)處理；全連接層包含一個線性激活函數(shù)，用來連接送入網(wǎng)絡(luò)的數(shù)據(jù)標(biāo)簽值和卷積網(wǎng)絡(luò)學(xué)習(xí)到的數(shù)據(jù)特征.

2.3 基于殘差學(xué)習(xí)的并聯(lián)反演模型

提高分辨率亦可以通過預(yù)測低分辨率解與真實解之間的差異，去除Radon卷積核的模糊作用(Ongie et al.,2020).該方法通過學(xué)習(xí)低分辨率共軛解與真實解之間的殘差，實現(xiàn)分辨率提高.通常采用跳躍連接網(wǎng)絡(luò)實現(xiàn)差異預(yù)測，例如殘差網(wǎng)絡(luò)，多級跳躍連接的U-net網(wǎng)絡(luò)等，這些網(wǎng)絡(luò)在提高圖像辨率、數(shù)據(jù)預(yù)測應(yīng)用中表現(xiàn)良好.為了方便與反褶積模型工作原理比對，本文設(shè)計如圖4所示的簡單一級跳躍殘差網(wǎng)絡(luò)結(jié)構(gòu)，該網(wǎng)絡(luò)與低分辨率數(shù)據(jù)形成并聯(lián)關(guān)系，與串聯(lián)模型呼應(yīng)稱之為并聯(lián)反演模型.

圖4 并聯(lián)反褶積模型Fig.4 Parallel deconvolution model

由圖4可得到并聯(lián)反演神經(jīng)網(wǎng)絡(luò)模型F2與Radon褶積核函數(shù)關(guān)系為：

(F2+I)Φ=I，(13)

即：

F2=CNN(Φ)=Φ-1-I，(14)

由此可以看到并聯(lián)網(wǎng)絡(luò)表示的是Hessian逆矩陣的變化部分.

上述并聯(lián)型網(wǎng)絡(luò)模型輸出低分辨率數(shù)據(jù)與神經(jīng)網(wǎng)絡(luò)輸出之和：

=BN(mH+CNN(mH))，(15)

串聯(lián)模型中網(wǎng)絡(luò)學(xué)習(xí)的是Radon變換反褶積算子，而并聯(lián)模型中網(wǎng)絡(luò)學(xué)習(xí)的為高分辨率解與低分辨率解之間的殘差.本文從兩個不同角度設(shè)計網(wǎng)絡(luò)，以尋求較好的網(wǎng)絡(luò)實現(xiàn)高分辨率Radon變換，并解釋神經(jīng)網(wǎng)絡(luò)反演的工作機理.

2.4 頻率約束

由于褶積算子Φ與頻率有關(guān)，而不同頻率對應(yīng)不同的Radon算子，使得卷積網(wǎng)絡(luò)實現(xiàn)的是單一頻率低分辨率解到真實解的映射.若要實現(xiàn)所有頻率的映射，就需要訓(xùn)練不同頻率的數(shù)據(jù)，得到對應(yīng)頻率的網(wǎng)絡(luò)，工作量較大.為此，本文引入頻率約束的思想(Chen and Lu,2011)，將網(wǎng)絡(luò)訓(xùn)練得到的單個頻率的結(jié)果約束其他所有頻率的反演，這里將網(wǎng)絡(luò)結(jié)果作為Radon反演先驗信息嵌入迭代加權(quán)最小二乘法，以此來減少工作量，提高計算效率.最終基于網(wǎng)絡(luò)的高分辨率Radon變換求解公式為：

(16)

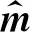
3 數(shù)據(jù)實驗

為驗證本文卷積網(wǎng)絡(luò)的可行性和有效性，本文將建立的一維卷積網(wǎng)絡(luò)用于處理模擬數(shù)據(jù)和實際地震數(shù)據(jù)多次波分離實驗，并與傳統(tǒng)的迭代加權(quán)最小二乘法求解的高分辨率Radon變換進行比較.本文中網(wǎng)絡(luò)訓(xùn)練環(huán)境為Intel Core i5-8300H CPU，主頻2.30 GHz，內(nèi)存16 GB，GPU為NVIDIA GeForce GTX 1050 with Max-Q Design.

3.1 數(shù)據(jù)集準(zhǔn)備

假設(shè)圖5a是模擬的待分離一次波和多次波簡單合成記錄，圖5b是其Radon參數(shù).為反演Radon參數(shù)，提高網(wǎng)絡(luò)性能，需要模擬相同分布的大量訓(xùn)練數(shù)據(jù).在真實Radon參數(shù)周圍隨機選擇一些Radon參數(shù)，由此生成一組與所求Radon參數(shù)分布類似的數(shù)據(jù)，變換到頻域后選擇主頻對應(yīng)的Radon參數(shù)作為標(biāo)簽數(shù)據(jù).之后利用式(6)得到其對應(yīng)的低分辨率共軛解作為輸入數(shù)據(jù)，與標(biāo)簽數(shù)據(jù)共同構(gòu)成數(shù)據(jù)集，以這種方式共生成11000個數(shù)據(jù)樣本，其中10000個樣本作為訓(xùn)練集，剩余1000個樣本作為測試集.串聯(lián)網(wǎng)絡(luò)模型和并聯(lián)網(wǎng)絡(luò)模型數(shù)據(jù)集相同，即以低分辨率共軛解作為輸入數(shù)據(jù)，其對應(yīng)的實際解作為標(biāo)簽數(shù)據(jù).

真實Radon參數(shù)和其對應(yīng)的低分辨率解為復(fù)數(shù)，而網(wǎng)絡(luò)訓(xùn)練數(shù)據(jù)為實數(shù).為此，本文將復(fù)數(shù)的實部和虛部串聯(lián)轉(zhuǎn)化為實數(shù)，一同送入網(wǎng)絡(luò).

3.2 數(shù)據(jù)實驗

圖5a為主頻30 Hz的Ricker子波合成的CMP地震道集，共50道，采樣點為500個，采樣間隔2 ms，它包含三個一次波同相軸，零偏移時間分別為0.2 s、0.5 s和0.8 s，以及四個多次波同相軸，零偏移時間分別為0.1 s、0.3 s、0.5 s和0.7 s，圖5b為其對應(yīng)的Radon域參數(shù).本文使用Keras建立串聯(lián)型和并聯(lián)型一維卷積網(wǎng)絡(luò)，并基于Tensorflow進行測試訓(xùn)練，兩個網(wǎng)絡(luò)都使用Adam算法來優(yōu)化學(xué)習(xí)目標(biāo)，采用均方誤差損失函數(shù)，設(shè)置初始學(xué)習(xí)率為0.001，epoch為80次，Batch size為20.

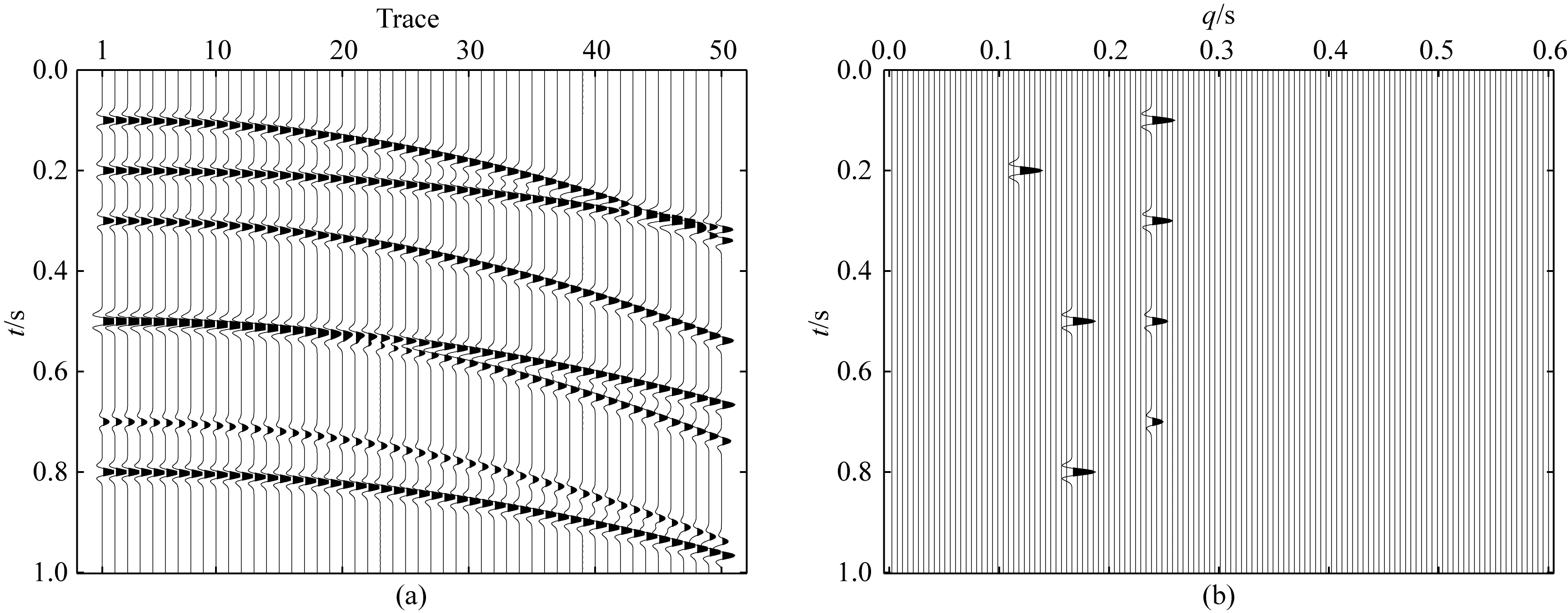
圖5 模擬地震數(shù)據(jù)(a) 模擬地震數(shù)據(jù)； (b) 模擬Radon參數(shù).Fig.5 The synthetic seismic data(a) The synthetic seismic data； (b) The synthetic Radon model.

本文采用信噪比(Signal-to-Noise Ratio, SNR)衡量Radon變換地震數(shù)據(jù)的恢復(fù)效果以及對多次波的壓制效果，信噪比定義為：

(17)

式中dr指原始地震數(shù)據(jù)或者原始一次波數(shù)據(jù)，dm指各種方法恢復(fù)的地震數(shù)據(jù)或恢復(fù)的一次波數(shù)據(jù).

3.2.1 卷積層屬性對網(wǎng)絡(luò)性能的影響

為了得到較好的反演效果，以原始數(shù)據(jù)重構(gòu)和一次波分離信噪比作為參考指標(biāo)，測試了不同卷積層屬性對結(jié)果的影響.

表1和表2分別為卷積層屬性對串聯(lián)型網(wǎng)絡(luò)和并聯(lián)型網(wǎng)絡(luò)的影響.對于串聯(lián)型卷積網(wǎng)絡(luò)，本文采用的卷積核大小為3×1，步長為1，卷積層后為ReLU激活函數(shù).從表1可以看到，如果每個卷積層都包含16個卷積核，則當(dāng)網(wǎng)絡(luò)深度為5即網(wǎng)絡(luò)有四個卷積層時網(wǎng)絡(luò)性能最佳，此時對多次波的壓制效果最好，地震數(shù)據(jù)恢復(fù)的信噪比與其他網(wǎng)絡(luò)層數(shù)恢復(fù)的信噪比接近；對于相同的網(wǎng)絡(luò)深度，當(dāng)采用混合卷積核，即表1中卷積層個數(shù)為5，卷積核個數(shù)依次為8、16、32、64、128時，網(wǎng)絡(luò)性能要弱于每個卷積層中卷積核個數(shù)都為16時的網(wǎng)絡(luò)性能，且網(wǎng)絡(luò)訓(xùn)練耗時更長.為此本文搭建的串聯(lián)型網(wǎng)絡(luò)結(jié)構(gòu)包含5個卷積層，每個卷積層中包含16個卷積核，卷積核大小為3×1，步長為1，激活函數(shù)為ReLU函數(shù).

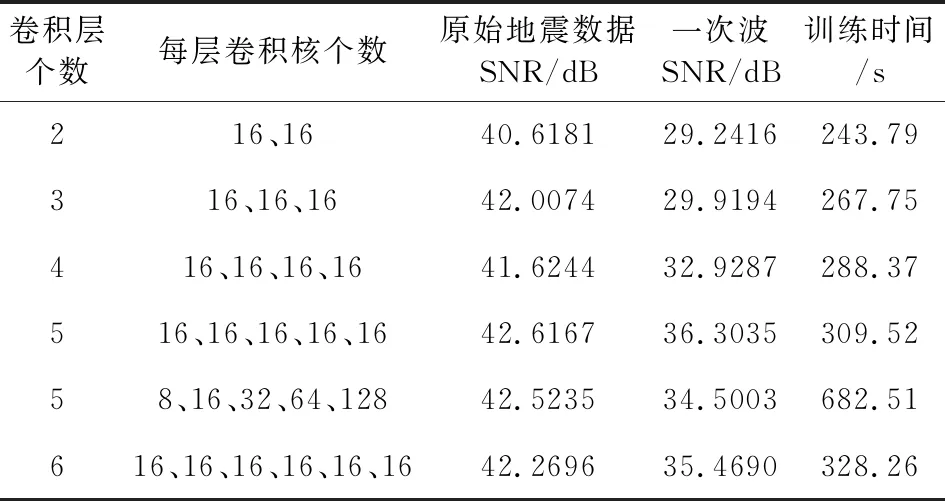
表1 卷積層屬性對串聯(lián)型網(wǎng)絡(luò)性能的影響Table 1 Influence of convolution layer on serial network

并聯(lián)型卷積網(wǎng)絡(luò)測試結(jié)果如表2中所示.當(dāng)每個卷積層都包含16個卷積核，且網(wǎng)絡(luò)含有5個卷積層時，網(wǎng)絡(luò)對多次波壓制效果最好，當(dāng)網(wǎng)絡(luò)采用混合卷積核，即表2中網(wǎng)絡(luò)卷積層個數(shù)為5，卷積核個數(shù)依次為8、16、32、64、128時，與全為16個卷積核的網(wǎng)絡(luò)相比，兩者都能有效壓制多次波，但其網(wǎng)絡(luò)訓(xùn)練時間大幅增加.綜合考慮對多次波的壓制效果以及網(wǎng)絡(luò)效率，本文搭建的并聯(lián)型網(wǎng)絡(luò)同樣采用5個卷積層，每個卷積層包含16個卷積核，卷積核大小為3×1，步長為1，卷積層之后為ReLU激活函數(shù).

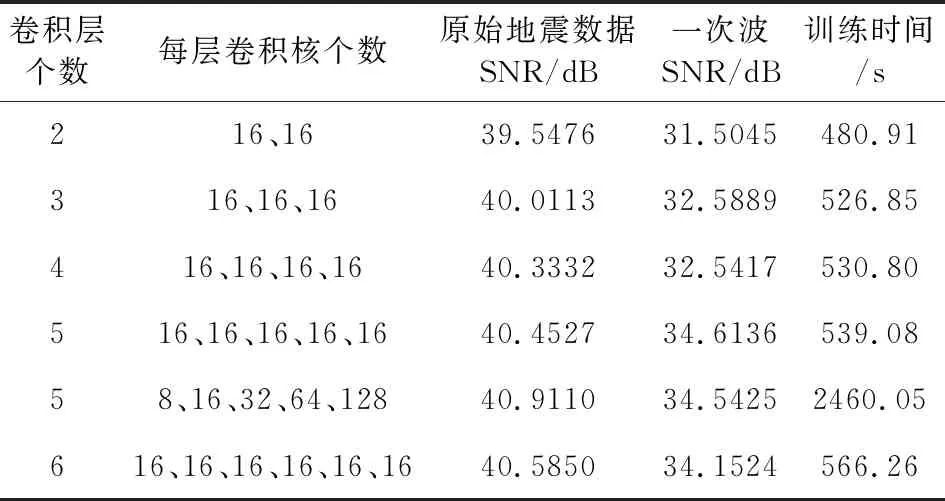
表2 卷積層屬性對并聯(lián)型網(wǎng)絡(luò)性能的影響Table 2 Influence of convolution layer on parallel network

3.2.2 模擬數(shù)據(jù)反演結(jié)果

首先，對頻率30 Hz的Radon參數(shù)進行反演，串聯(lián)型一維卷積網(wǎng)絡(luò)、并聯(lián)型一維卷積網(wǎng)絡(luò)以及迭代加權(quán)最小二乘法反演結(jié)果如圖6a所示，圖6b為圖6a中圓圈部分局部放大后圖像.從圖中可以看到，串聯(lián)網(wǎng)絡(luò)得到的數(shù)據(jù)可以很好的擬合真實數(shù)據(jù)，并聯(lián)網(wǎng)絡(luò)得到的數(shù)據(jù)會在真實值附近有擾動，但兩者都要優(yōu)于IRLS恢復(fù)的數(shù)據(jù).

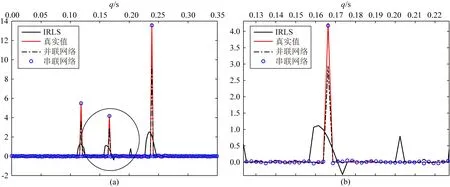
圖6 30 Hz數(shù)據(jù)反演結(jié)果(a) 完整結(jié)果圖； (b) 局部放大圖.Fig.6 The inversion result of 30 Hz data(a) Complete graph； (b) Partial graph.

為更好地理解神經(jīng)網(wǎng)絡(luò)特征提取的作用，本文將兩種網(wǎng)絡(luò)第3層特征圖提出示意于圖7.由圖7a可看到，串聯(lián)模型期望提出的特征圖最后組合成稀疏的反演結(jié)果，其特征圖多數(shù)是稀疏分布的；而并聯(lián)模型學(xué)習(xí)到的是稀疏模型與低分辨率波形的差異，變化較大，因此特征圖變化劇烈，如圖7b所示，導(dǎo)致其對真實數(shù)據(jù)的擬合程度要弱于串聯(lián)模型.圖8為兩者訓(xùn)練集和測試集的準(zhǔn)確率和損失值，從圖中觀察得到，串聯(lián)模型和并聯(lián)模型在20次epoch時幾乎收斂，實驗發(fā)現(xiàn)，隨著網(wǎng)絡(luò)的進一步訓(xùn)練，對多次波的壓制效果會有所提升，為此本文epoch設(shè)置為80次.從圖8中也可以觀察得到，串聯(lián)模型訓(xùn)練集以及測試集的準(zhǔn)確率要高于并聯(lián)模型，損失值要小于并聯(lián)模型，進一步表明并聯(lián)模型對數(shù)據(jù)的擬合程度要弱于串聯(lián)網(wǎng)絡(luò)模型.同樣的，無論串聯(lián)網(wǎng)絡(luò)還是并聯(lián)網(wǎng)絡(luò)，兩者測試集的準(zhǔn)確率都要好于訓(xùn)練集的準(zhǔn)確率，測試集的損失值也要小于訓(xùn)練集的損失值，即兩者都有較強的泛化能力.

獲得主頻數(shù)據(jù)之后，用該頻率數(shù)據(jù)約束其他頻率的反演，從而得到所有頻率的Radon參數(shù).三種方法反演得到的Radon參數(shù)如圖9a、b、c所示.觀察圖9a—c可以得到，網(wǎng)絡(luò)反演得到的Radon參數(shù)能量要比IRLS得到的Radon參數(shù)能量更加集中，即網(wǎng)絡(luò)可以更好的分離一次波和多次波Radon參數(shù).之后由Radon反變換可得到三種方法恢復(fù)的地震數(shù)據(jù)如圖9d、e、f，圖9g、h、i為三者與真實地震數(shù)據(jù)值的誤差.表3列出了三種反演方法的重構(gòu)結(jié)果，結(jié)合圖9以及表3，可以觀察到串聯(lián)型網(wǎng)絡(luò)恢復(fù)的數(shù)據(jù)與真實地震數(shù)據(jù)的誤差最小，其次為并聯(lián)型網(wǎng)絡(luò)，兩者均要好于IRLS恢復(fù)的地震數(shù)據(jù).

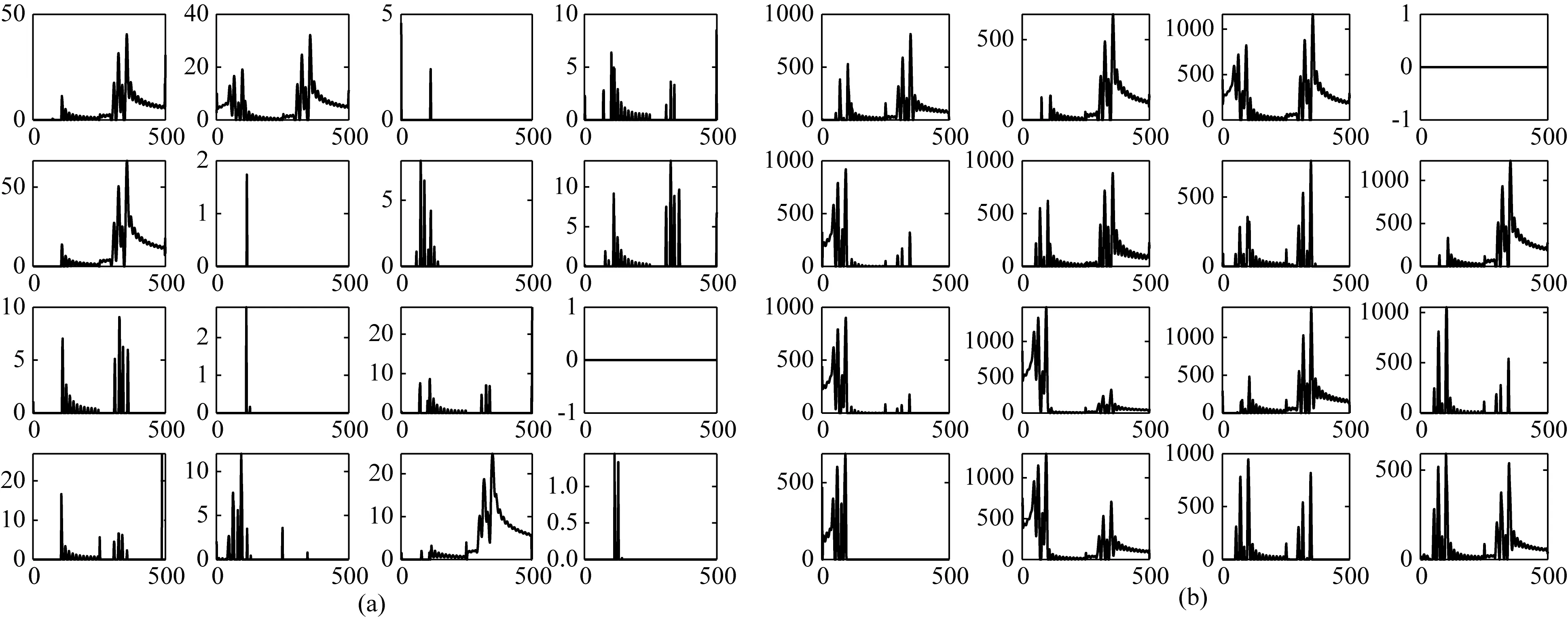
圖7 網(wǎng)絡(luò)特征圖(a) 串聯(lián)網(wǎng)絡(luò)模型； (b) 并聯(lián)網(wǎng)絡(luò)模型.Fig.7 Network characteristic map(a) Series network model； (b) Parallel network model.

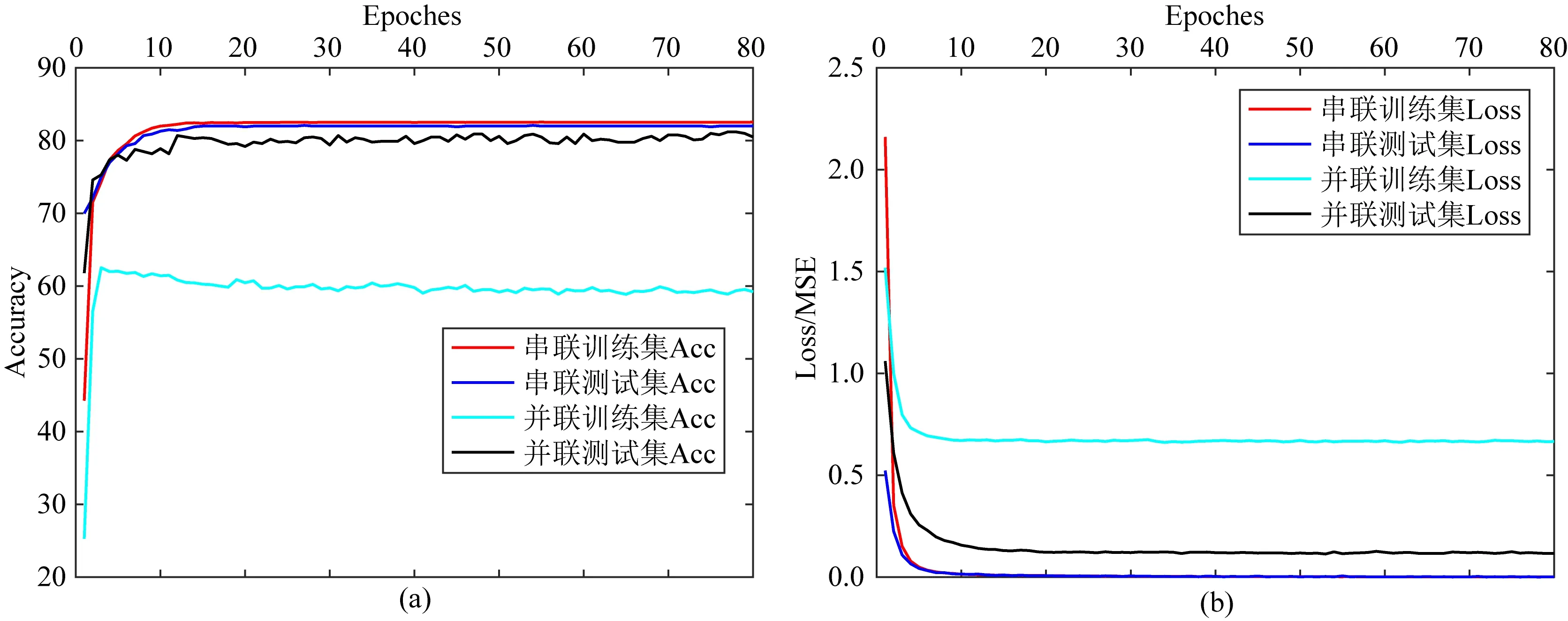
圖8 網(wǎng)絡(luò)訓(xùn)練集和測試集的準(zhǔn)確率及損失值(a) 網(wǎng)絡(luò)訓(xùn)練集和測試集的準(zhǔn)確率； (b) 網(wǎng)絡(luò)訓(xùn)練集和測試集的損失值.Fig.8 Accuracy and loss value of network training set and test set(a) Accuracy of network training set and test set； (b) Loss of network training set and test set.

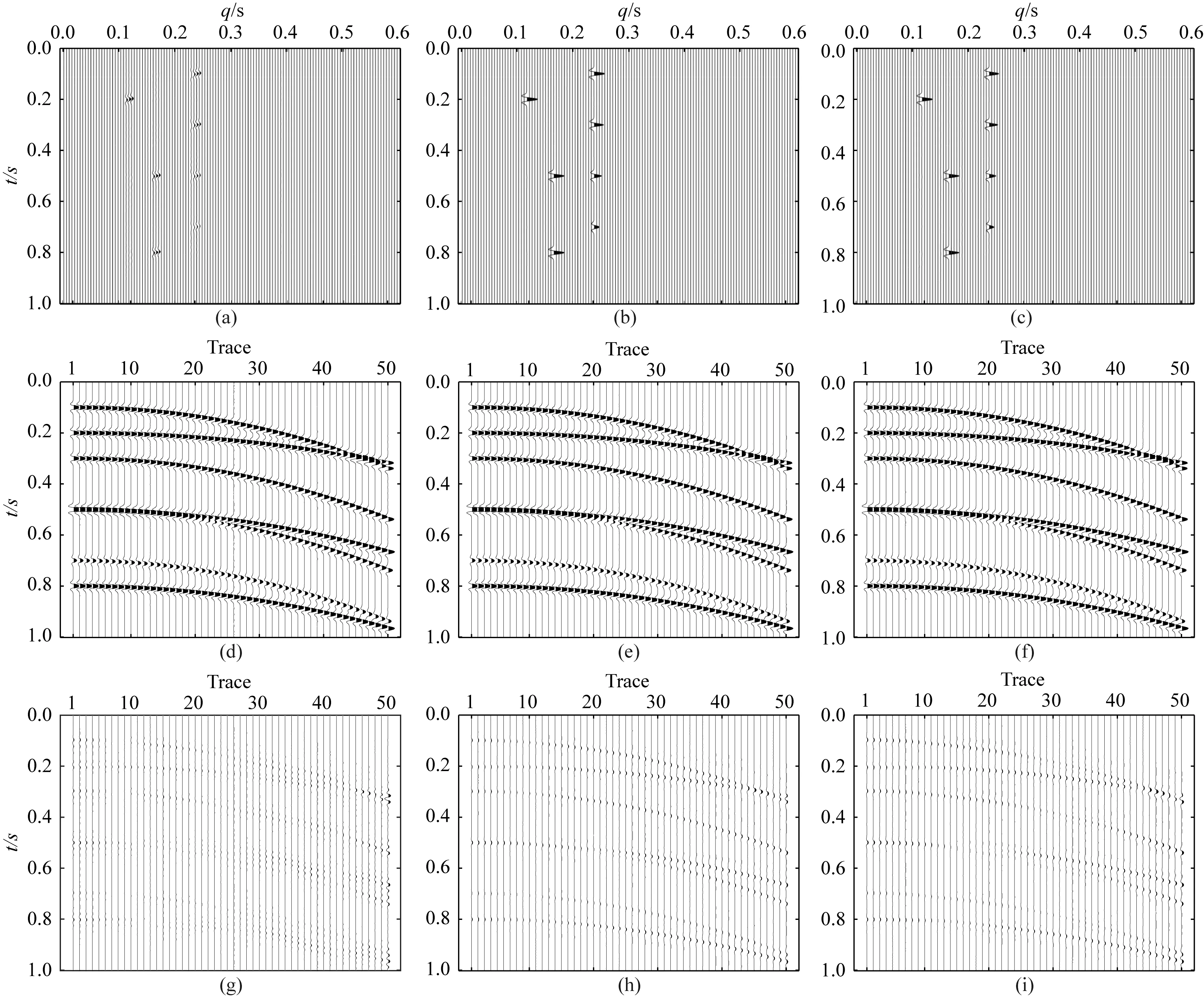
圖9 模擬數(shù)據(jù)對比(a) IRLS方法反演的Radon參數(shù)； (b) 串聯(lián)網(wǎng)絡(luò)反演的Radon參數(shù)； (c) 并聯(lián)網(wǎng)絡(luò)反演的Radon參數(shù)； (d) IRLS方法恢復(fù)的地震數(shù)據(jù)； (e) 串聯(lián)網(wǎng)絡(luò)恢復(fù)的地震數(shù)據(jù)； (f) 并聯(lián)網(wǎng)絡(luò)恢復(fù)的地震數(shù)據(jù)； (g) IRLS恢復(fù)的地震數(shù)據(jù)的誤差(放大10倍)； (h) 串聯(lián)型網(wǎng)絡(luò)恢復(fù)的地震數(shù)據(jù)的誤差(放大10倍)； (i) 并聯(lián)型網(wǎng)絡(luò)恢復(fù)的地震數(shù)據(jù)的誤差(放大10倍).Fig.9 Comparison of synthetic data(a) The Radon model obtained by IRLS； (b) The Radon model obtained by serial 1-D CNN； (c) The Radon model obtained by parallel 1-D CNN； (d) Seismic data obtained by IRLS； (e) Seismic data obtained by serial 1-D CNN； (f) Seismic data obtained by parallel 1-D CNN； (g) The difference between the true and the data obtained by IRLS (10x)； (h) The difference between the true and the data obtained by serial 1-D CNN (10x)； (i) The difference between the true and the data obtained by parallel 1-D CNN (10x).

在三種方法得到Radon域參數(shù)之后，濾除一次波參數(shù)，經(jīng)Radon反變換可得到時域多次波數(shù)據(jù)，從原始數(shù)據(jù)減去多次波數(shù)據(jù)即可得到壓制多次波后的結(jié)果.三種方法估計的一次波數(shù)據(jù)見圖10a、b、c，其與真實一次波數(shù)據(jù)的誤差如圖10d、e、f所示.由圖10和表3可以得到，串聯(lián)型網(wǎng)絡(luò)可以保留更多的一次波信息，其一次波信噪比最高，其次為并聯(lián)型網(wǎng)絡(luò)，兩者都好于IRLS方法保留的一次波信息.

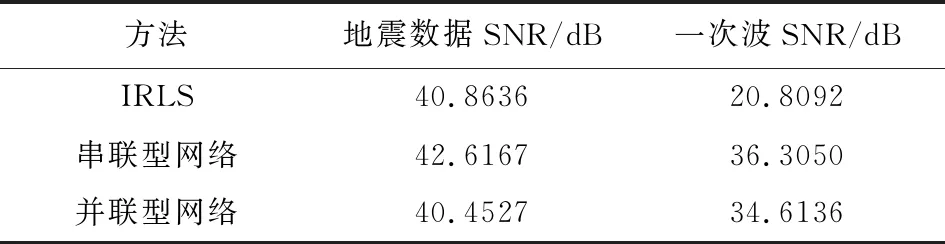
表3 三種方法估計地震數(shù)據(jù)的信噪比Table 3 The SNR of seismic data estimated by three methods

3.2.3 實際數(shù)據(jù)

為了進一步驗證本文方法的有效性，對如圖11a所示動校正三維地震數(shù)據(jù)進行多次波壓制實驗.該數(shù)據(jù)包含13炮數(shù)據(jù)，每炮25道，每道2501個采樣點，采樣間隔2 ms.圖11b為圖11a按炮點距離排序之后的地震數(shù)據(jù)，可以看到地震數(shù)據(jù)中含有明顯的傾斜多次波.對于實際地震數(shù)據(jù)，可由最小二乘方法得到Radon參數(shù)，之后從中隨機抽取一定量的Radon參數(shù)組成新的Radon域數(shù)據(jù)，變換到頻域后選取主頻對應(yīng)的Radon參數(shù)作為標(biāo)簽數(shù)據(jù)，其對應(yīng)的低分辨率共軛解作為輸入數(shù)據(jù)，兩者組成數(shù)據(jù)集.以此生成1100個數(shù)據(jù)集，其中1000個作為訓(xùn)練集，100個作為測試集.在模擬數(shù)據(jù)網(wǎng)絡(luò)訓(xùn)練的基礎(chǔ)上，凍結(jié)卷積層訓(xùn)練參數(shù)，只對網(wǎng)絡(luò)最后的全連接層進行訓(xùn)練，從而對網(wǎng)絡(luò)進行微調(diào).

圖10 一次波數(shù)據(jù)對比(a) IRLS方法估計的一次波數(shù)據(jù)； (b) 串聯(lián)型網(wǎng)絡(luò)估計的一次波數(shù)據(jù)； (c) 并聯(lián)型網(wǎng)絡(luò)估計的一次波數(shù)據(jù)； (d) IRLS方法估計的一次波數(shù)據(jù)誤差(放大10倍)； (e) 串聯(lián)型網(wǎng)絡(luò)估計的一次波數(shù)據(jù)誤差(放大10倍)； (f) 并聯(lián)型網(wǎng)絡(luò)估計的一次波數(shù)據(jù)的誤差(放大10倍).Fig.10 Comparison of primaries(a) The primaries obtained by IRLS； (b) The primaries obtained by serial 1-D CNN； (c) The primaries obtained by parallel 1-D CNN； (d) The difference between the true and the primaries obtained by IRLS (10x)； (e) The difference between the true and the primaries obtained by serial 1-D CNN (10x)； (f) The difference between the true and the primaries obtained by parallel 1-D CNN(10x).

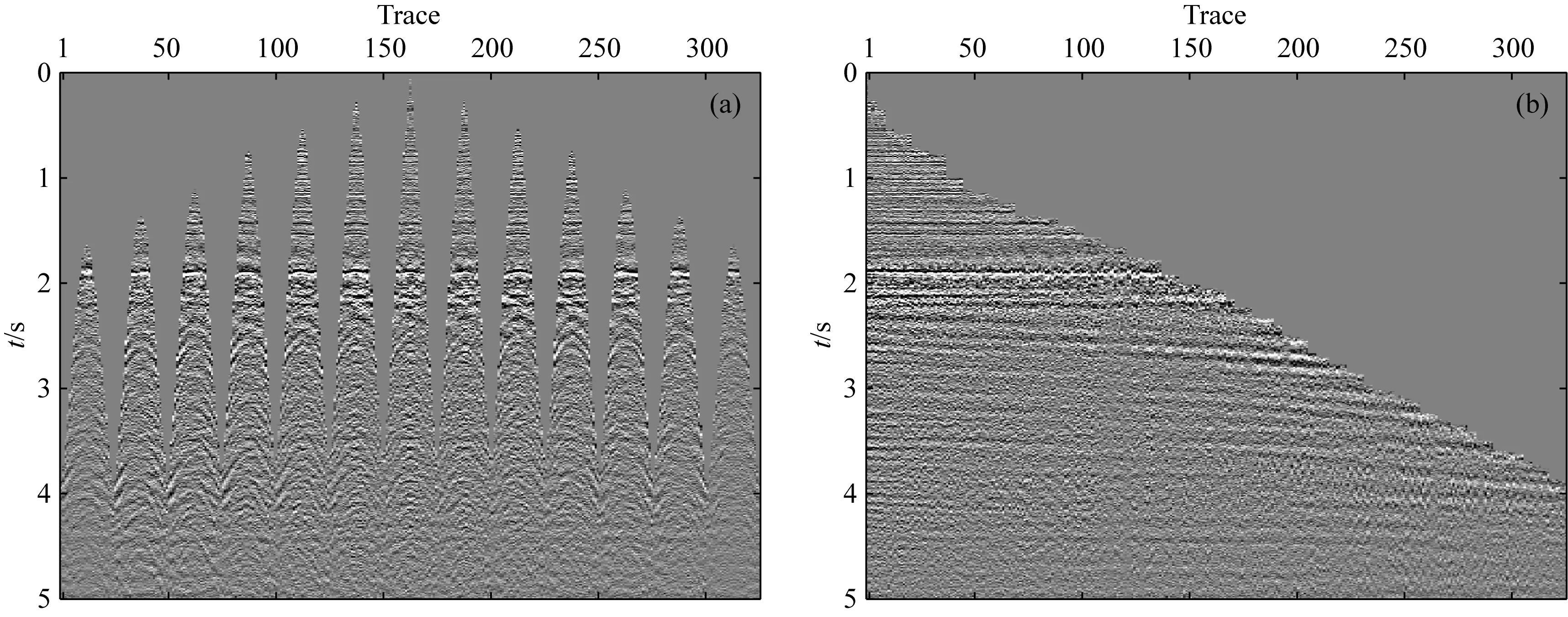
圖11 實際地震數(shù)據(jù)(a) 實際地震數(shù)據(jù)； (b) 按炮點距排序后的實際地震數(shù)據(jù).Fig.11 The field data(a) The field data； (b) The field data sorted by scalar offset.

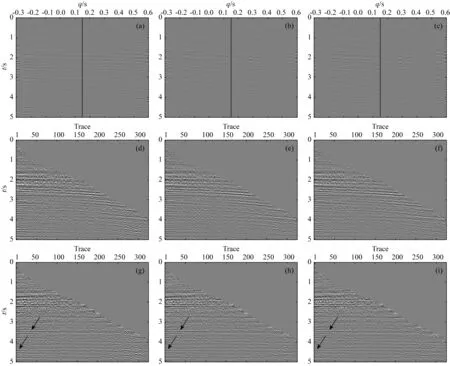
圖12 三種方法處理后的地震數(shù)據(jù)(a) IRLS方法反演的Radon參數(shù)； (b) 串聯(lián)網(wǎng)絡(luò)反演的Radon參數(shù)； (c) 并聯(lián)網(wǎng)絡(luò)反演的Radon參數(shù)； (d) IRLS得到的多次波； (e) 串聯(lián)網(wǎng)絡(luò)得到的多次波； (f) 并聯(lián)網(wǎng)絡(luò)得到的多次波；(g) IRLS方法壓制多次波后的數(shù)據(jù)； (h) 串聯(lián)網(wǎng)絡(luò)壓制多次波后的數(shù)據(jù)； (i) 并聯(lián)網(wǎng)絡(luò)壓制多次波的數(shù)據(jù).Fig.12 The field data processed by three methods(a) The Radon model obtained by IRLS； (b) The Radon model obtained by serial 1-D CNN； (c) The Radon model obtained by parallel 1-D CNN； (d) The multiple obtained by IRLS； (e) The multiple obtained by serial 1-D CNN； (f) The multiple obtained by parallel 1-D CNN； (g) The primaries obtained by IRLS； (h) The primaries obtained by serial 1-D CNN； (i) The primaries obtained by parallel 1-D CNN.

采用IRLS、串聯(lián)型和并聯(lián)型高分辨率Radon變換分別處理圖11所示的實際地震數(shù)據(jù)，結(jié)果如圖12所示.圖12a—c為三種方法反演得到第8炮數(shù)據(jù)的Radon參數(shù)，可以觀察得到，串聯(lián)網(wǎng)絡(luò)模型和并聯(lián)網(wǎng)絡(luò)模型兩者得到的Radon參數(shù)分辨率基本相當(dāng)，都要優(yōu)于傳統(tǒng)IRLS得到的Radon參數(shù)分辨率，與模擬數(shù)據(jù)結(jié)果一致.

切除0.15 s以下的Radon參數(shù)，可得到多次波對應(yīng)的Radon參數(shù)，經(jīng)Radon反變換可得到時域多次波數(shù)據(jù)，如圖12d—f所示.從原始數(shù)據(jù)減去Radon反演得到的多次波數(shù)據(jù)，即可得到實際地震數(shù)據(jù)壓制多次波后的結(jié)果，三種方法壓制多次波后的結(jié)果如圖12g—i所示.觀察圖12g、h、i中箭頭所指部分可以發(fā)現(xiàn)，串聯(lián)網(wǎng)絡(luò)、并聯(lián)網(wǎng)絡(luò)以及傳統(tǒng)IRLS都能很好的壓制多次波，其中IRLS運行時間為1407 s，串聯(lián)網(wǎng)絡(luò)得到單個頻率Radon參數(shù)后進行多次波壓制運行時間為102 s，并聯(lián)網(wǎng)絡(luò)得到單個頻率Radon參數(shù)后進行多次波壓制運行時間為101 s，即串并聯(lián)網(wǎng)絡(luò)模型運行時間基本相同，都要遠小于傳統(tǒng)IRLS方法，這是由于傳統(tǒng)IRLS計算時需要進行大量的矩陣求逆運算，導(dǎo)致消耗大量時間.

4 結(jié)論

本文通過建立Radon變換的卷積模型，借助卷積神經(jīng)網(wǎng)絡(luò)的非線性表征能力實現(xiàn)Radon變換的高分辨率反演.建立了串聯(lián)型和并聯(lián)型兩種神經(jīng)網(wǎng)絡(luò)結(jié)構(gòu)，串聯(lián)型網(wǎng)絡(luò)實現(xiàn)了Radon變換反褶積算子的功能，而并聯(lián)型網(wǎng)絡(luò)學(xué)習(xí)的是低分辨率解與真實解的殘差，兩者通過不同的路徑實現(xiàn)了低分辨率解到高分辨率解的映射.實驗結(jié)果證明串聯(lián)網(wǎng)絡(luò)模型和并聯(lián)網(wǎng)絡(luò)模型都具有較好的應(yīng)用效果，其中串聯(lián)網(wǎng)絡(luò)性能要略優(yōu)于并聯(lián)網(wǎng)絡(luò)模型.

與傳統(tǒng)高分辨率Radon變換反演方法相比，基于卷積神經(jīng)網(wǎng)絡(luò)的方法不需要借助參數(shù)先驗信息，只需要為網(wǎng)絡(luò)送入相應(yīng)的訓(xùn)練數(shù)據(jù)，網(wǎng)絡(luò)就能夠?qū)W習(xí)其中的數(shù)據(jù)特征，實現(xiàn)所求低分辨率數(shù)據(jù)到高分辨的映射.在效率方面，網(wǎng)絡(luò)主要耗時在數(shù)據(jù)訓(xùn)練過程，而在網(wǎng)絡(luò)訓(xùn)練好之后，就能夠利用網(wǎng)絡(luò)來快速求解相關(guān)問題，即網(wǎng)絡(luò)可以重復(fù)利用.本文通過模擬數(shù)據(jù)和實際數(shù)據(jù)的驗證，表明基于卷積神經(jīng)網(wǎng)絡(luò)的方法來實現(xiàn)高分辨率Radon變換是可行的，神經(jīng)網(wǎng)絡(luò)在地震資料領(lǐng)域的運用為高分辨率Radon變換的實現(xiàn)提供了新的發(fā)展方向.