200米彎道跑技術(shù)分析

陳全林

（濰坊學(xué)院 體育學(xué)院，山東 濰坊 261061）

1 前言

200米跑分為兩部分，彎道跑和直道跑 ，彎道跑的距離是114.04米，直道跑的距離是85.96米。彎道跑占了一大部分，所以彎道跑技術(shù)動作和場地的影響是不可忽視的，技術(shù)動作方面是能夠通過運(yùn)動員自身努力學(xué)習(xí)，達(dá)到非常標(biāo)準(zhǔn)的水平，但是場地器材方面，不同跑道的影響是運(yùn)動員無法控制的，不是隨運(yùn)動員的意志為轉(zhuǎn)移的。假如此問題存在，這對運(yùn)動員就不公平了。所以本文在生物力學(xué)方面，從理論上進(jìn)行分析，不同跑道彎道跑之間是否具有差異性。以及對濰坊學(xué)院二級運(yùn)動員徐煥文同學(xué)不同跑道的實(shí)測數(shù)據(jù)通過T檢驗(yàn)進(jìn)行分析，看不同跑道之間是否具有顯著性差異。假如此問題成立，然后給出一些合理化的建議。

2 研究方法

2.1 文獻(xiàn)資料法

在濰坊學(xué)院圖書館收集了關(guān)于200米彎道跑的所有中外文獻(xiàn)資料

2.2 生物力學(xué)分析法

本文以濰坊學(xué)院2019級二級運(yùn)動員徐煥文同學(xué)為研究對象，并在第一，四，八跑道上跑整個(gè)彎道，采集數(shù)據(jù)來研究本課題。

2.3 體育統(tǒng)計(jì)法

讓徐煥文同學(xué)每天在第一，四，八道上跑一次彎道跑，測出記下成績，連續(xù)測二十天，得到二十組數(shù)據(jù)，然后用T檢驗(yàn)看不同跑道之間是否具有顯著性差異。

3 結(jié)果與分析

3.1 第一、四和八道上彎道跑時(shí)力學(xué)分析

物體在做圓周運(yùn)動時(shí)，物體的速度方向是和圓周的切線方向一致，并且是不斷的變化的，存在向心加速度，方向指向圓心其大小為a=V2/r(V為線速度、r為半徑)。運(yùn)動員在彎道上跑步時(shí)做圓周運(yùn)動，速度方向和大小時(shí)刻變化，此時(shí)運(yùn)動員必受到一個(gè)外力的作用，這個(gè)外力的方向始終沿著半徑指向圓心，這個(gè)力和速度方向垂直，這個(gè)力就是向心力。大小為：F=ma=mv2/r。人體在彎道上跑動時(shí)，向心力由地面與運(yùn)動員之間的支撐反作用力N與重力G的合力F來提供。

可以看出，物體做圓周運(yùn)動的話，它一定要受到一個(gè)與速度方向垂直的外力，這樣物體才會時(shí)刻的改變運(yùn)動方向。如果這個(gè)力和速度方向一致，物體就只改變速度的大小，物體就只會做變速直線運(yùn)動。同樣人體在彎道上跑，就是一種圓周運(yùn)動，這時(shí)就需要一個(gè)向心力來改變?nèi)梭w的運(yùn)動方向，人體的這個(gè)向心力要靠人體的向內(nèi)傾斜來提供。這個(gè)向心力為支撐反作用力N與重力G的合力F，F(xiàn)即為人體在彎道上跑時(shí)時(shí)刻改變速度方向的向心力，如果沒有向心力F的作用，人體便會朝著跑道的切線方向運(yùn)動，就不會跑出弧線。

人體在彎道上跑動時(shí)，一個(gè)人的身體必需是傾斜的，而在直道上跑動時(shí)人體不向左右兩側(cè)傾斜，只向前方稍微傾斜，如果把直道跑看成是半徑無限大時(shí)的彎道跑，這樣便可得到，隨著半徑的增大，身體的傾斜程度會逐漸變小，并且所需的向心力也會逐漸變小。外側(cè)跑道身體傾斜程度小于內(nèi)側(cè)跑道。人體在直道上跑動時(shí)，腿部各大肌群都在做快速收縮舒張運(yùn)動，髖、膝、踝三關(guān)節(jié)做伸展、折疊運(yùn)動。而每次做功都可以在原基礎(chǔ)上進(jìn)行完全疊加，能夠達(dá)到本人的最高速度。而在彎道上跑動時(shí)，速度方向每一步都是在改變的，所以人體做的功不能完全疊加，所以在彎道上的最高速度要比在直道上的最高速度要小一些。可以知道在外道跑時(shí)的最高速度，要比在內(nèi)道跑時(shí)的最高速度值要大一些。從內(nèi)、外跑道所需的向心力的大小上也可以驗(yàn)證這個(gè)結(jié)論。由公式F=mv2/r可計(jì)算出一名體重為69千克，彎道速度為10米/秒的運(yùn)動員，在場地半徑為36米的第一、四、八跑道上跑動時(shí)，所受到的向心力為：

可得：

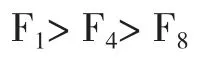
由以上數(shù)據(jù)可以看出，同一名運(yùn)動員用同樣的速度，在不同的跑道上跑，所需的向心力是不同的。由內(nèi)往外所需的向心力逐漸變小，所以，在內(nèi)道上跑要比在外道上跑費(fèi)力。因?yàn)檫@個(gè)向心力的最佳提供方式是由身體傾斜來完成，外側(cè)跑道上跑所需的向心力小，所以運(yùn)動員向內(nèi)的傾斜程度也就小，內(nèi)側(cè)跑道上跑所需的向心力大，所以運(yùn)動員向內(nèi)的傾斜程度也就大。因此，跑進(jìn)方向上的力外側(cè)跑道比內(nèi)側(cè)跑道就大一些，并且容易維持身體平衡，有利于彎道跑時(shí)的加速和提高成績。

3.2 測量在第一、四和八道上跑整個(gè)彎道距離114.04米所用的時(shí)間，并進(jìn)行比較

有人做過試驗(yàn)，在直線跑道上跑200米所用的時(shí)間，要比在半徑為42.06米的彎-直道上跑200米所有的時(shí)間少0.4s（統(tǒng)計(jì)學(xué)均值）[2]，這是已經(jīng)被證實(shí)了的事實(shí)。美國人P?詹英經(jīng)研究發(fā)現(xiàn)，在彎道上與在直線跑道上跑等量距離，兩者所需時(shí)間之差與跑道的半徑成反比。即:

這里Tr是半徑為42.06米的彎道跑時(shí)間，Ts是半徑無限大時(shí)，既等量直道跑所用時(shí)間。把半徑42.06和差值0.4s代入上式可得出：K=16.824。

由（1）式可推導(dǎo)出跑第m條彎道與跑第n條彎道所需時(shí)間之差為：

這樣由式（2）可以計(jì)算出跑第一、四和八道之間的時(shí)間差分別是：

下面對濰坊學(xué)院體育學(xué)院2019級學(xué)生徐煥文進(jìn)行了測試，分別測得在第一、四和八道彎道上跑114.04米時(shí)的二十組數(shù)據(jù)并進(jìn)行比較（見表1、圖1）。看在第一、四和八道上彎道跑是否具有顯著性差異。

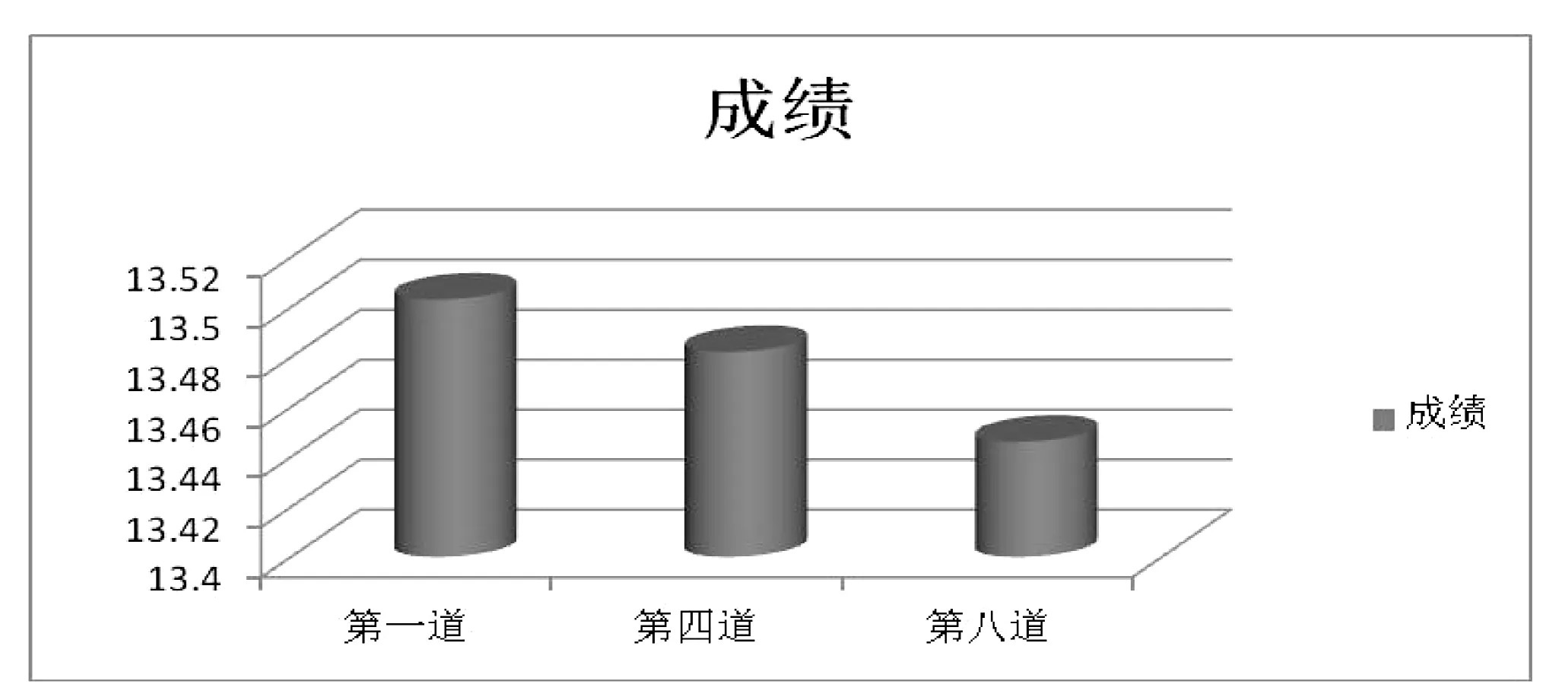
圖1 彎道跑成績柱狀圖比較

表1 徐煥文在不同跑道跑時(shí)的時(shí)間平均數(shù)（單位:s）

從表1可以看出第一道的平均成績是13.503s，第四道的平均成績是13.482s，第八道的平均成績是13.446s。不同跑道的平均成績是不一樣的，從外往里依次變差。由P值為0，則P<0.01可以看出，在第一，四和八跑道上跑，它們之間的差異是非常顯著的。

從表1和圖1也可以直觀看出跑外道優(yōu)于跑內(nèi)道，從所測數(shù)據(jù)可看出，彎道跑時(shí)間第一道比第四道多用0.021s，第一道比第八道多用0.057s。這一數(shù)據(jù)和美國人P·詹英所得數(shù)據(jù)稍有不同，沒有P·詹英的數(shù)據(jù)大一點(diǎn)，原因是不同水平運(yùn)動員之間所得出的數(shù)據(jù)是不同的。水平越高這一數(shù)字越大，也就是在內(nèi)、外道跑時(shí)成績的差異越大。

4 結(jié)論與建議

（1）在短跑現(xiàn)規(guī)則中，比賽時(shí)成績好的前四名運(yùn)動員分在跑道的中間四條跑道，成績稍差的四名運(yùn)動員分在跑道兩邊的四條跑道。這樣忽略了跑道對運(yùn)動員的影響，建議按上一輪比賽的成績，由成績好的運(yùn)動員優(yōu)先選擇跑道。也可以按跑道由里往外分別安排成績差到成績好來排列。這樣更有利于運(yùn)動員發(fā)揮運(yùn)動水平，創(chuàng)造出更好的成績，也不至于把成績好的運(yùn)動員因跑道不好而被淘汰。

（2）建議在200米彎道訓(xùn)練時(shí)，均衡的用每一條跑道訓(xùn)練，這樣可以使運(yùn)動員體會每一道的傾斜程度和運(yùn)動感覺。并且還能夠增加第一跑道使用壽命，因?yàn)殚L距離跑項(xiàng)目都是在第一道上跑，這樣也相當(dāng)于延長了整個(gè)田徑場的使用壽命。