基于XGBoost的短時交通流預測研究

焦朋朋，安 玉,2，白紫秀，林 坤,3

(1. 北京建筑大學 北京未來城市設計高精尖創新中心，北京 100044; 2. 北京市市政工程設計研究總院有限公司，北京 100082； 3. 福州市規劃設計研究院集團有限公司，福建 福州 350000)

0 引 言

目前已有較多模型方法用于短時交通流預測，主要包括：基于統計分析的方法、非線性理論的方法、仿真的方法、人工智能領域的方法以及組合模型的方法。傳統的基于時間序列的研究方法是利用差分自回歸移動平均(ARIMA)[1]。隨著交通流數據采集設備的升級和計算機計算能力的提升，應用神經網絡等復雜的機器學習模型進行高精度的交通流預測成為可能，特別是基于循環神經網絡的LSTM模型[2]在短時交通流預測中獲得廣泛應用。隨著研究的深入，模型的預測精度逐漸提高，但模型復雜度也越來越高。

J.WANG等[3]假設在一個預測周期內，交通流僅與前幾個周期的交通流相關，運用自回歸綜合移動平均、卡爾曼濾波和反向傳播神經網絡的方法，建立新的貝葉斯模型，達到了更好的預測結果；羅文慧等[4]結合卷積神經網絡與支持向量回歸分類器，達到精準且快速的短時交通流預測的目的；Y .TIAN等[5]針對檢測器的缺陷導致的采樣不規則和缺少數據的問題，提出了一種基于LSTM的方法，采用多尺度時平法來推斷丟失的數據，得到較高預測精度的結果；S .CHENG 等[6]認為在交通流預測時只考慮指定時間段內相鄰路段之間的相關性，很難取得穩定的結果，提出了自適應時空K近鄰模型，根據自適應空間鄰域、時間窗口、時空權重等參數，綜合考慮城市交通的空間異質性；廖榮華等[7]使用改進鄰近相點選取的混沌時間序列局域法對交通數據進行了分析預測并取得了較高的精度；康軍等[8]對預測的不確定性進行定量分析，提出基于高斯過程回歸的短時交通流預測方法，可得到預測值的方差估計值以及95%置信區間。

深度學習的興起再度為交通流預測提供了新的思路。CNN和RNN及其衍生模型均在深度學習[9]中具有廣泛的應用，并有突出的效果；王祥雪等[10]在深度學習的理論框架下，構建基于 LSTM-RNN的城市快速路短時交通流預測模型，利用交通流的時空相關性完成時間序列的重構；S .DENG等[11]利用交通流的時空流量關系構造二維圖卷積神經網絡，將時間序列分析問題轉化為圖像分析任務，預測結果得到較高的精度；S.GUO[12]針對空間和時間的關聯性和異質性，提出3D 圖卷積神經網絡，捕獲流量數據的相關性提高精度。但是，深度學習方法受參數選擇影響較大，工作量大，計算時間長；Q. HOU等[13]考慮到交通流的周期性和變異性和單個預測模型的局限性，提出一種自適應的短時交通流混合預測模型，采用ARIMA和非線性小波神經網絡(WNN)將兩個模型輸出進行模糊邏輯分析和組合，對交通流進行預測；與此同時，E. I .VLAHOGIANNI等[14]提出目前在短時交通流預測研究的探索之中，對于模型方法的選擇要注重模型的解釋力、方法的合理性、提高數據的質量、充分利用交通流數據的時間特性與空間相關性。當前大多數預測方法的主要問題是精度和計算量的矛盾，精度高的預測方法一般計算量大，計算量小的預測方法精度不高，如何在計算量和精度之間取得平衡是一個關鍵[15]。

針對交通流預測問題中模型復雜度與預測精度的矛盾，筆者提出采用集成學習思想的XGboost方法進行短時交通流預測。集成學習的思想是：一個弱可學習的問題經過多項式時間計算得到強可學習的問題。與神經網絡模型[16-17]不同，為提升預測精度XGBoost集成多個CART決策樹的弱學習器，每個弱學習器以上一步的預測殘差作為逼近目標，加入正則項控制模型的復雜度以防止過擬合提高模型的泛化能力。XGboost方法具有可視化，適用于高維的樣本的特點，適用于交通流變化影響因素較多的情況。

1 交通流數據預處理

采集設備硬件問題、車輛故障、不當的駕駛行為等會造成設備采集到的原始數據出現缺失和錯誤。因此，為了較好的預測效果需要對原始數據進行適當的缺失數據補全。

流量數據存在異常的0值，占有率數據存在異常的100%，速度數據存在異常的大于80 km/h，此類異常數據類似椒鹽噪聲。椒鹽噪聲是數字信號處理與數字圖像處理中常見的一種噪聲，它是一種隨機出現的白點或者黑點，對應交通流數據的異常極大值、極小值。

因此，選取常用的中值濾波預處理椒鹽噪聲，其特點是將信號中的每個值都替換為其鄰域內的中值，即鄰域內所有值排序后中間位置的值。中值濾波的優勢是仍能保留交通流的變化趨勢且減少數據噪聲導致的極大值、極小值，對脈沖噪聲有良好的濾除作用，特別是在濾除噪聲的同時，能夠保護信號的邊緣，使之不被模糊。

2 XGBoost預測模型建立

XGBoost的原理是構造多個弱學習器，第1個基學習器擬合樣本數據，擬合的誤差作為第2個基學習器的目標繼續擬合，以此類推，最后把所有基學習器累加，類似統計學上的殘差逼近，如式(1)。Boosting是減少偏置的模型組合方式，可以達到較高的預測精度。

(1)

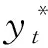
2.1 模型框架

從第t-1棵樹到第t棵樹目標函數為當前預測結果Ft-1(xi)+ft(xi)與yi之間的差距，增加正則化項，得到XGBoost的目標函數，如式(2)：

(2)

式中：L[yi,Ft-1(xi)+ft(xi)]為真實值yi與近似函數Ft-1(xi)+ft(xi)的差距；Ω(ft)為正則項，表示樹的復雜度，用來避免過擬合，如式(3)：

(3)

式中：γ為對整棵樹葉節點的正則，目的是用來控制葉節點的個數，削弱每顆樹的權重，讓后面的樹有更大的學習空間；T為每棵樹葉子節點數量；λ為控制葉節點維度的正則；ω為葉子節點列向量；ωj為葉子節點j的權值。

對L[yi,Ft-1(xi)+ft(xi)]使用二階泰勒展開如式(4)：

(4)

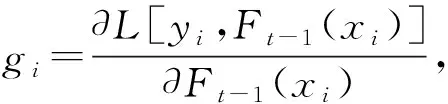
由于t-1輪的結果是已知的，可以不做考慮，簡化后目標函數如式(5)：

(5)

進一步將正則化項展開并合并，且從n個樣本遍歷改至從葉子節點j遍歷，如式(6)：

(6)

對式(6)求最小值可以得到ωj的最優值和損失函數最小值，如式(7) 、式(8)：

(7)

(8)

式(8)可以看作對決策樹不純度的衡量，也是作為樹節點分裂的依據，即衡量節點在分裂前后式(6)對應數值的大小用以判斷是否需要繼續分裂。

綜上所述，XGBoost的建樹過程、Boosting過程均是以目標函數為基礎進行的，一切操作的衡量標準均是最小化目標函數，其采用的算法策略是貪心策略。由于引入了泰勒二階展開，建樹與Boosting的過程僅依賴于損失函數的一階導數與二階導數，因此可以支持自定義損失函數。XGBoost優勢是將正則項加入到了目標函數中，保證了每次的迭代均對模型的復雜度進行了對沖，有效降低了過擬合發生的可能性，此外支持并行處理、近似算法等，可提高模型的計算效率。

2.2 模型數據

交通流的基本參數直接反映路段的交通狀態，筆者將路段的流量作為預測目標進行研究，路段流量是指在第n時段內，通過觀測斷面的所有車輛數的累計。路段平均速度和平均占有率分別為第n時段內，通過觀測斷面的所有車輛的平均值，其計算方式如式(9)：

(9)

模型數據集的特征包括上下游斷面流量、密度和時間占有率等參數，均以固定5 min時間周期進行計算。

2.3 性能指標

為更好分析計算結果，筆者選擇平均絕對誤差(MAE)、均方誤差(MSE)和決定系數(R2)作為模型的性能指標，如式(10)～式(12)：

(10)

(11)

(12)

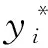
2.4 流 程

筆者利用XGBoost模型對路段流量進行預測。預測的基本思路是：提取斷面過車數據，分析相鄰上游斷面上一時段的流量、速度及占有率數據，進行斷面過車流量預測。具體步驟為：

步驟1將通過微波檢測設備得到的海量過車數據，通過統計方法以一定的時間窗格對每個斷面統計其過車流量、速度及占有率，構造多維時間序列。

步驟2對每個斷面的數據進行中值濾波處理，補全缺失數據并適當降低數據的異常波動。

步驟3將濾波后數據劃分為訓練集和測試集，訓練集輸入XGBoost模型進行訓練，使用交叉驗證的方法調整超參數以建立最優的模型。

步驟4將測試集數據輸入模型得到斷面流量預測值，與其他短時交通流預測方法的預測值進行對比分析。

3 實例分析

3.1 案例數據

選取合肥市一段城市道路的過車數據，數據源自OpenITS的開源數據。合肥示范區位于經濟技術開發區黃山路沿線，潮汐交通特征明顯。示范區范圍包括以下路段：黃山路、香樟大道、天柱路、科學大道、天智路和天湖路。示范區布設有微波交通流檢測設備。微波檢測數據包括編號、設備類型、設備編號、采集時間、時間占有率等多個字段信息，數據詳情如表1。

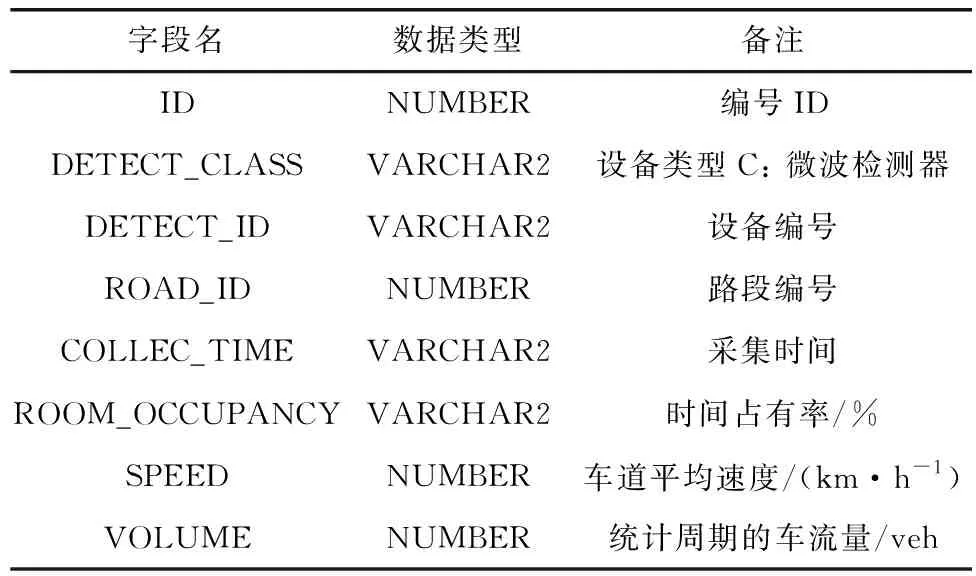
表1 交通流原始數據統計內容匯總Table 1 Summary of statistical content of original traffic flow data

其中，設備編號DETECT_ID與路網交叉口的對應關系如圖1，微波檢測設備主要檢測主路的4個車道，并實時返回交通流數據。其中，由于采集設備硬件問題、車輛故障、不當的駕駛行為等造成設備采集到的原始數據出現缺失和錯誤共占比3.7%，且異常數據不存在大段數據缺失問題。

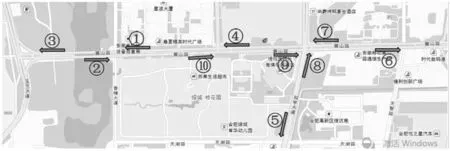
圖1 設備編號DETECT_ID的位置示意Fig. 1 Location diagram of device DETECT_ID

3.2 數據處理

將原始數據處理成以5 min為周期的時間序列數據。使用python的pandas庫對原始數據計算流量、速度、占有率的時間序列。以1號斷面的qt流量數據為預測目標(根據交通流的空間相關性，模型輸入選擇1號、4號、7號、8號斷面上一時段流量qt-1、速度Vt-1、占有率Ot-1數據。選擇2016年7月1日—2016年7月5日數據作為訓練數據，選擇7月6日數據作為測試數據。

利用Scipy庫中signal 對原始數據進行中值濾波平滑處理，處理前后時間序列數據對比如圖2，可以看出濾波后異常值明顯減少，更加能滿足模型的需要。

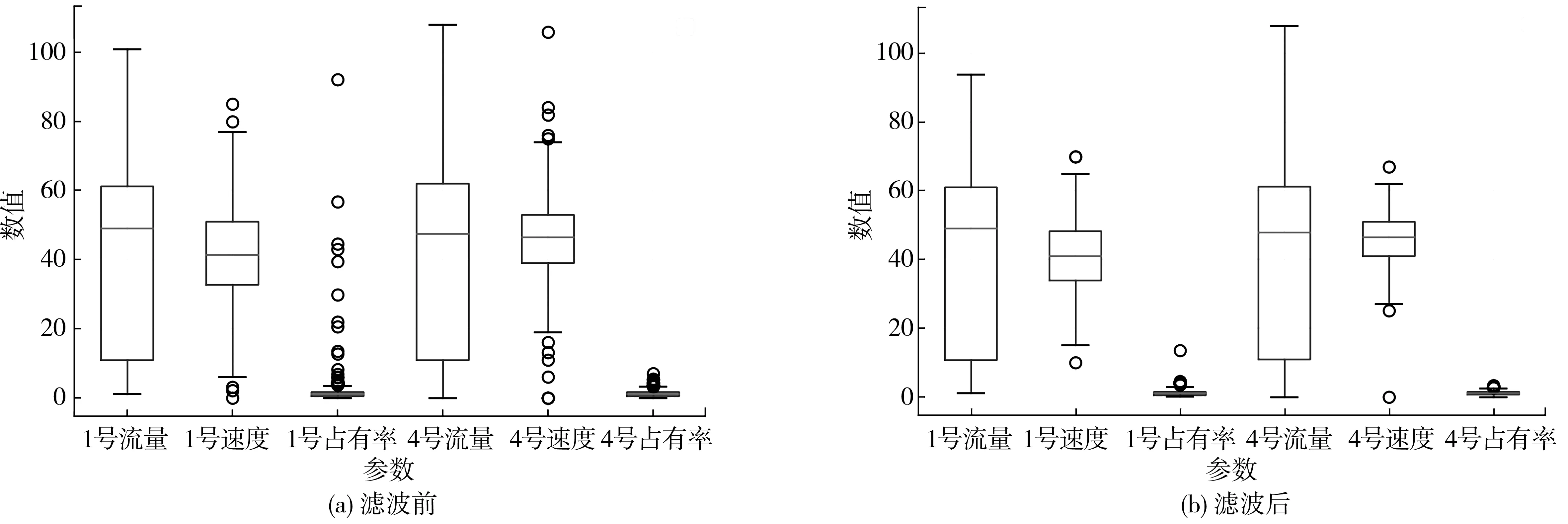
圖2 濾波前后數據對比Fig. 2 Data comparison before and after filtering

3.3 特征間相關性

為判斷模型的輸入數據時間和1號、4號、7號、8號斷面流量、速度、占有率數據之間的相關性，繪制相關系數熱力圖如圖3(特征前數字為卡口編號)。可以看出由于斷面間距較小，以5 min為周期的時間序列數據間相關性偏低，可以作為模型的輸入。

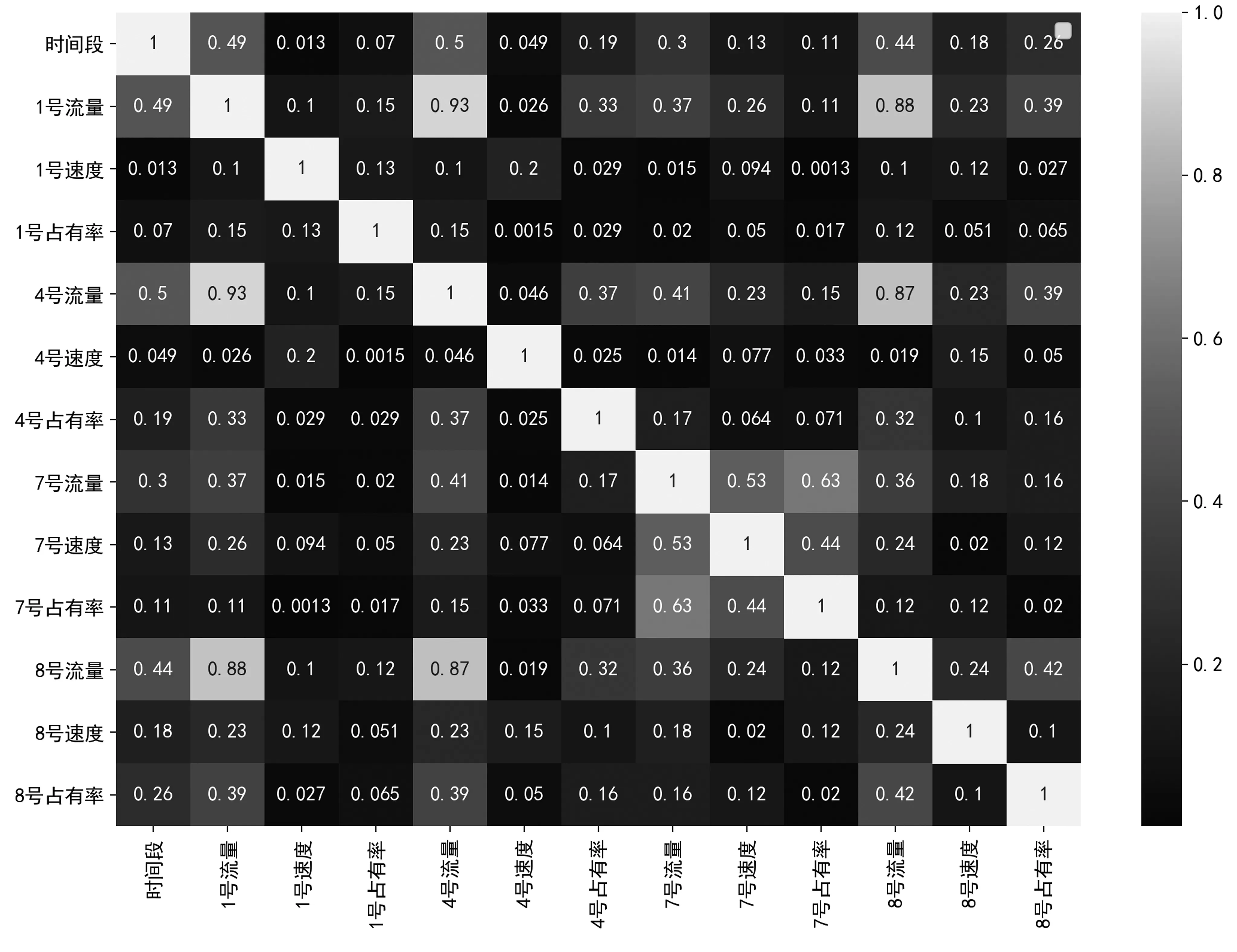
圖3 特征間的相關性Fig. 3 Correlation between features

3.4 模型超參數設置

模型參數是模型內部的配置變量，可以用樣本數據估計它的取值，而模型超參數是模型外部的配置，其值不能從樣本數據估計得到，需要針對目標問題通過反復試驗確定其最優取值。

模型的復雜度受數據規模的影響，模型復雜、數據較少會導致過擬合，模型簡單、數據較多會導致欠擬合，都會影響模型的預測效果。XGBoost有較多的超參數，這些超參數可以控制模型的規模，用來表征其復雜程度。

筆者采用交叉驗證的方法，確定數據規模對應的模型復雜程度。利用Scikit-learn庫包建立模型以及交叉驗證，以損失函數為評價指標選擇最優超參數取值。其中最小葉子節點權重與決策樹最大深度的取值示意如圖4。

圖4 超參數最佳取值Fig. 4 Best value of super-parameter

除最小葉子節點權重與決策樹最大深度外，XGBoost模型也支持正則化項、學習率、特征重采樣和樣本重采樣等。模型利用交叉驗證方法確定的超參數取值匯總如表2。

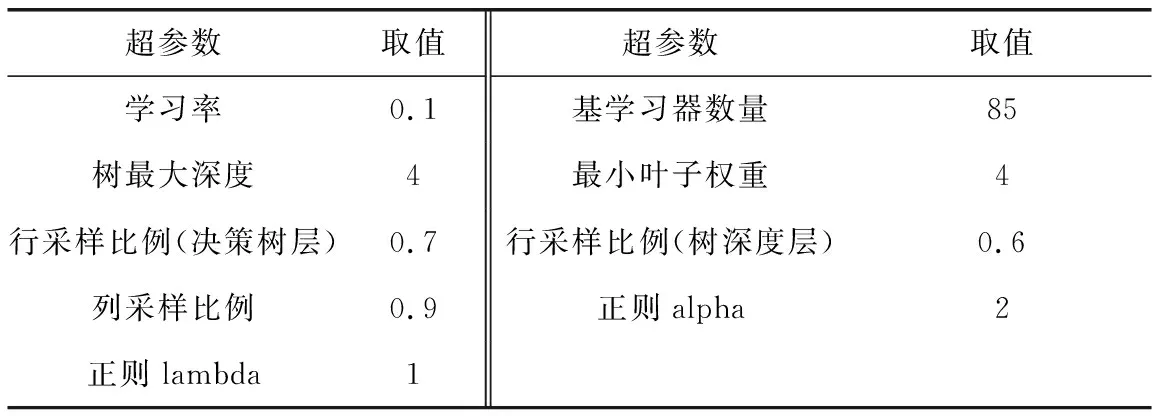
表2 超參數最佳取值匯總Table 2 Summary of super-parameter best value

3.5 模型預測結果分析

特征重要度可以反映模型的預測值受其輸入特征之間的映射關系，表征不同特征在預測時的重要程度，統計此模型的特征重要度如圖5。

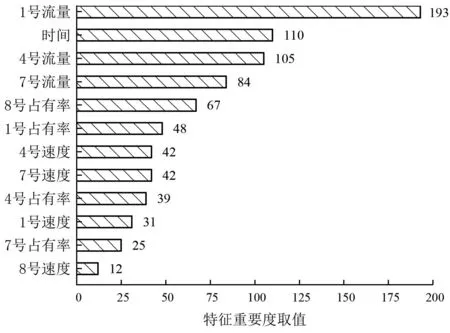
圖5 特征重要度匯總Fig. 5 Summary of feature importance

從圖5中可以看出各項特征均對預測模型造成一定影響，充分利用各項特征能達到提升預測精度的目的，反映出交通流時間序列的時間特性以及空間相關性對預測目標精度的重要性。

3.6 預測結果對比分析

為評估中值濾波處理對原始數據的清洗效果，以及對比XGBoost與LSTM對交通流數據空間相關性和時間相關性的利用效果，評估XGBoost與其他交通流預測常用方法的預測水平。

匯總不同方法在是否中值濾波進行訓練與預測后，性能指標情況與模型訓練時間對比情況如表3。其中XGBoost累積交叉驗證確定模型超參數以及訓練過程的時間為40.57 s，而確定超參數取值后單次訓練的時間僅為0.045 s。神經網絡模型的超參數學習率默認為0.01，epochs為50，batch為144。LSTM模型前2層LSTM神經元維數為12、64；第3層全連接層維數64；GRU模型前2層LSTM神經元維數為12、64，第3層全連接層維數為64；SAEs模型隱含層全連接層，維數分別為12、400、400、400；ARIMA模型，自回歸項p的取值為3，非季節性差異數d的取值為1，預測方程滯后預測q的取值為1。

根據表3結果分析如下：

1)對比表3中值濾波前后預測精度可以看出：中值濾波處理后原始數據的異常波動有明顯降低，使LSTM的預測精度提升3.8%，使XGBoost的預測精度提升5.5%。

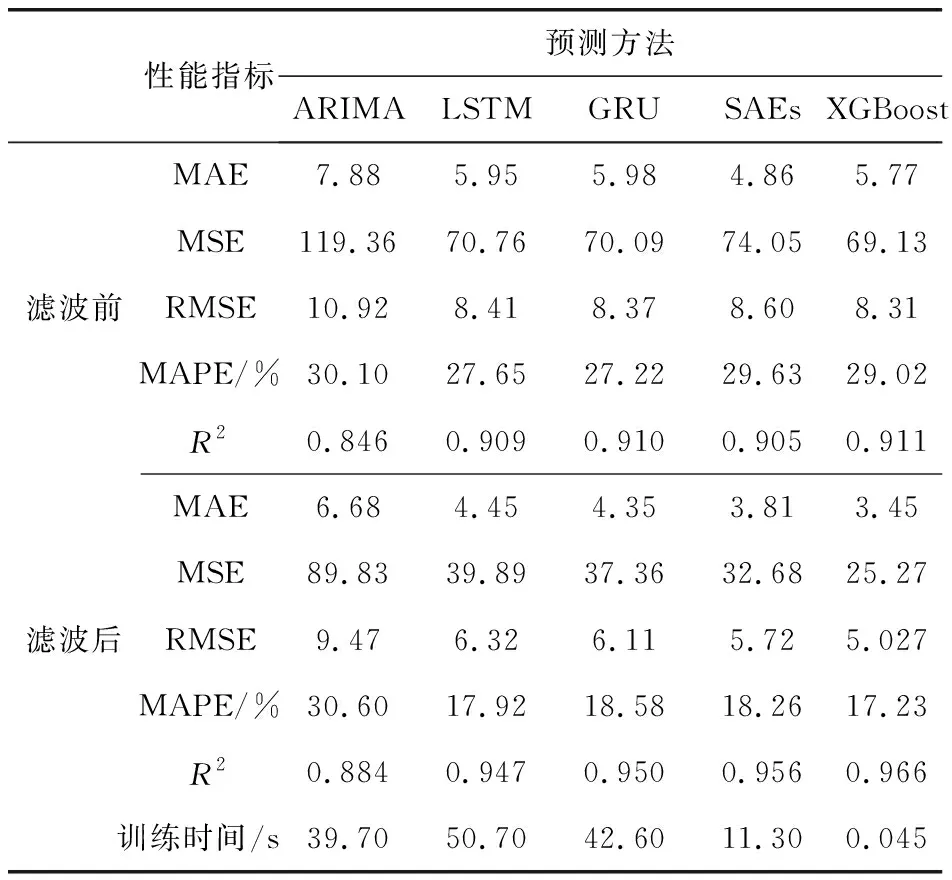
表3 濾波前后不同方法性能指標與訓練時長對比Table 3 Comparison of performance indexes and training durationof different methods before and after filtering

2)對比XGBoost與其他短時交通流預測方法的訓練時間可以看出，在預測精度水平相差不大情況下，XGBoost模型具有較高的計算速度，扣除因交叉驗證確定超參數而花費的時間，即訓練數據集確定后超參數也即確定，可認為文中模型訓練時間相比神經網絡模型速度快得多。

3)對比表3可以看出：神經網絡相關模型能充分利用交通流數據的周期特性，反映出循環神經網絡對時間周期性數據預測的優勢。但在利用多個特征的交通流數據時，XGBoost更能充分利用斷面上下游的空間相關性，精度比神經網絡相關模型高一些，反映出XGBoost能充分利用各個特征的優勢，更適用于解決交通流變化利用上下游數據提升預測精度的情況。

4 結 語

在短時交通流預測中，使用中值濾波處理缺失數據與異常數據，可以降低原始時間序列的異常波動，提高預測模型的精度。

相比神經網絡模型，XGBoost模型較為簡單，可以充分利用交通流的時間特性與空間相關性，將斷面的上下游數據作為高維特征，可以達到較高的預測精度，尤其適用于交通流波動時充分利用上游交通流數據進行高精度的預測。

利用相鄰4個斷面6天的交通流數據進行訓練與預測，可以適當反映出XGBoost模型適用于高維特征數據的優勢，但未考慮到擁堵狀態下下游斷面排隊車輛的蔓延對上游斷面交通流的影響，后續可深入研究。