基于SSA-VMD和熵的特征值提取方法*
韓星辰,趙柏山,慈賀迪
(1.沈陽工業大學信息科學與工程學院,沈陽 110870;2.吉林大學電子科學與工程學院,長春 130012)
1 引言
滾動軸承作為旋轉機械設備的基本核心部件之一,具有易損性高的特點。滾動軸承的振動信號也有著非平穩、非線性[1]的特征,在故障發生早期,會制造較大的噪聲干擾,故障信號極易淹沒在噪聲中。為了能夠直接準確地進行故障特征識別,就需要對軸承的振動信號進行故障特征提取。變分模態分解(VMD)方法能夠將多分量信號一次性分解成多個單分量調幅或調頻信號[2],從而克服了EMD算法中模態混疊和頻率特征不易分辨等問題,使分解出來的各個IMF分量更加清晰,方便后續處理。本研究即是基于這一方法,利用SSA加以優化,并結合熵,提出一種改進的特征值提取算法。
2 基于SSA-VMD和熵的特征提取
改進算法的整體流程如圖1所示。在流程開始之初,須采用SSA-VMD方法對信號進行分解。在麻雀搜尋算法(SSA)[3]中,每只麻雀均有三種可能的身份:一是負責覓食的發現者;二是負責跟隨發現者進行覓食的加入者;三是預警者,負責警戒偵查,有危險則通知種群放棄食物,一般預警者數量占整個種群的10%~20%。
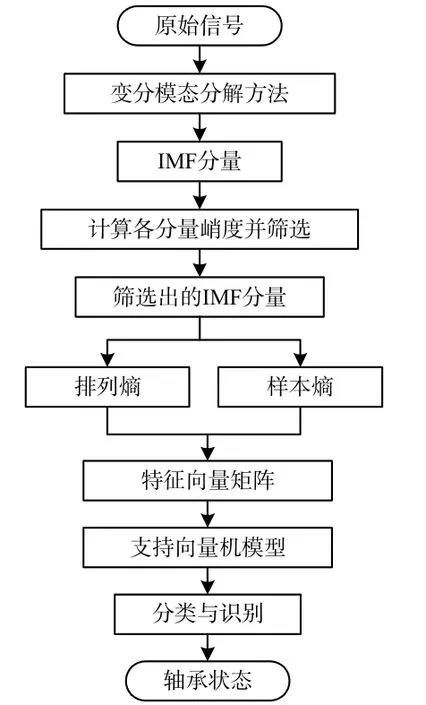
圖1 算法整體流程圖
以SSA對VMD進行優化[4-5]的具體實現步驟詳細如下:
a.對相關參數初始化,并隨機產生[k,α]組合作為麻雀種群的初始位置。
b.計算適應度值并排序,找到當前最優、最差的個體。
c.對種群中的發現者位置進行更新,其位置更新可表示為:
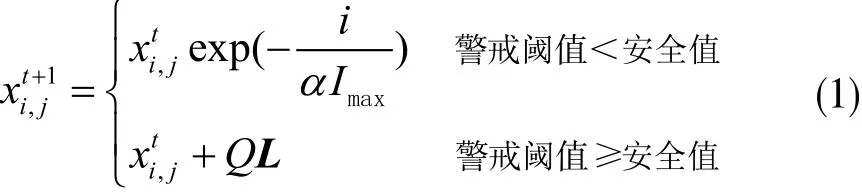
其中,t表示當前迭代次數;IMAX表示最大迭代次數。α表示(0,1]內一個隨機數;Q表示服從正態分布的隨機數;L表示大小為1×d、所有元素均為1的矩陣。對種群中的加入者位置進行更新,其位置更新可表示為:
其中,A表示大小為1×d、所有元素隨機賦值為1或-1的矩陣,A+為A的偽逆矩陣,即A+=AT(AAT)-1。xp為發現者所處最佳位置;xworst為全局最差位置。對種群中的預警者位置進行更新,表示為:
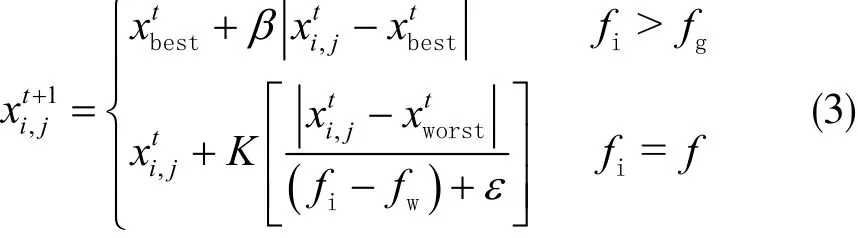
其中,K、β為步長控制參數;xbest為全局最優位置;fi為麻雀適應度值;fg為全局最佳適應度;fw為全局最差適應度;ε表示最小常數。
d.判斷是否終止,若不能終止,重復執行步驟b至d。
e.輸出最優個體位置[k,α]。
包絡熵值與信號中特征信息含量成正比,故將包絡熵作為SSA-VMD的適應度函數。包絡熵的定義為:
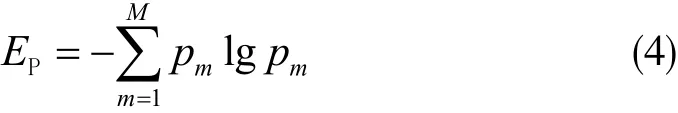
其中,pm表示對信號x(m)利用Hilbert解調變換的包絡信號歸一化處理。
利用峭度篩選分解后所得的IMF分量。峭度值通常是對信號中包含故障信息量的度量手段[6]。峭度越大,故障信息越多。峭度值的定義可以表示為:
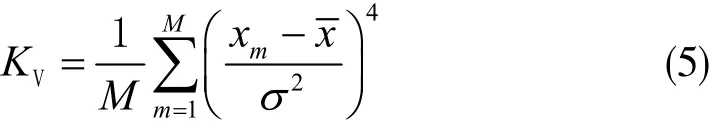
其中,x為信號xm的均值;M為采樣長度;σ為信號xm的標準差。對于正常軸承,KV=3。
至此,便可以構成特征向量矩陣,將能夠檢測信號是否存在動力學突變的排列熵與能夠反映信號復雜程度的樣本熵共同作為特征因素。
假設有時間序列{x(1),x(2),...,x(m)},排列熵可以表示為:
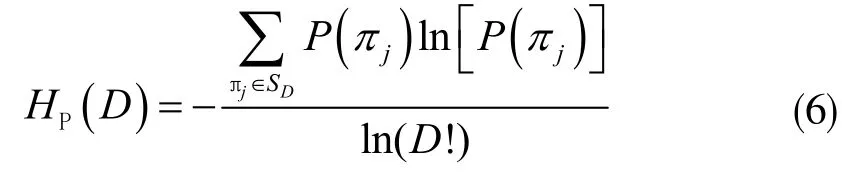
其中,D表示嵌入維數,將所有的可能排列集合記做SD;P(πj)表示每一類πj序列的概率。
樣本熵[7]可表示為:
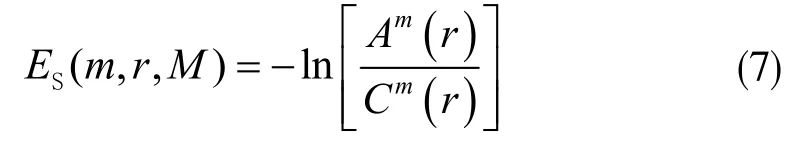
其中,r為相似容限閾值;Cm(r)與Am(r)分別表示構建m、m+1維向量中向量數d[xi+1,xj+1]<r與總向量數的比值的平均值。
3 實驗分析
采用美國凱斯西儲大學軸承數據(CWRU)進行實驗分析。實驗中采用數據的轉速為1797r/min,信號采樣頻率為12kHz。數據包括四種:正常狀態、內圈故障、外圈故障、滾動體故障。
令采樣長度N=1024;每種數據100個樣本,共計400個樣本。以滾動體故障數據為例,設種群大小n=30,最大迭代次數IMAX=200,安全值為0.6,發現者比例為種群的70%,預警者比例為種群的20%,其他為加入者。令α∈[100,4000],K∈[2,15],取噪聲容限為0,收斂容差為1.0×10-7,滾動體故障信號經SSA-VMD方法處理后,所得模態分量的時域圖與頻譜圖如圖2所示。
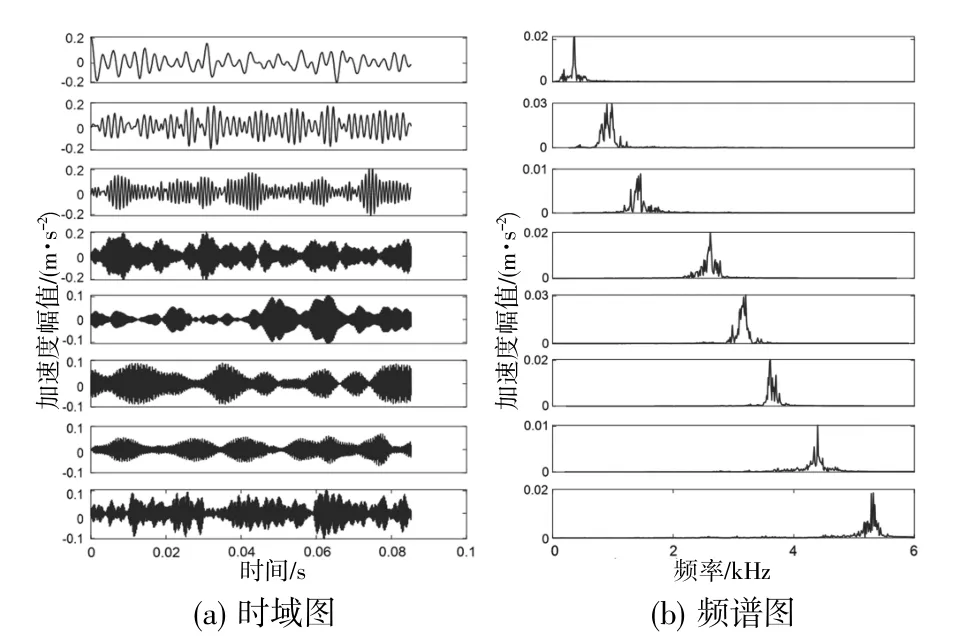
圖2 滾動體故障信號SSA-VMD處理效果
由圖可知,滾動體故障信號經過SSA-VMD處理后,獲得了信號分解出來的8個模態分量,每個分量都有一個對應的中心頻率。為進一步驗證SSAVMD方法的有效性,令其與PSO-VMD和GA-VMD進行對比。同樣以軸承的滾動體故障數據為例。令遺傳算法中交叉概率為0.8,變異概率為0.2,粒子群算法中學習因子皆為1,其他參數均與SSA-VMD相同,并且同樣將包絡熵作為適應度函數。三種算法的適應度函數迭代對比情況如圖3所示。

圖3 各算法適應度函數對比
可見,SSA-VMD算法的尋優速度優于POSVMD與GA-VMD。由適應度函數值可知,經SSAVMD方法處理后所得的IMF分量中,噪聲含量少于POS-VMD與GA-VMD。
SSA-VMD、POS-VMD、GA-VMD三者的各模態分量的中心頻率如圖4所示。由實驗結果可見,信號經過SSA-VMD方法分解所得到的各模態中心頻率之間相對獨立,有效地避免了模態混疊現象,得到了較為單純的本征模態。
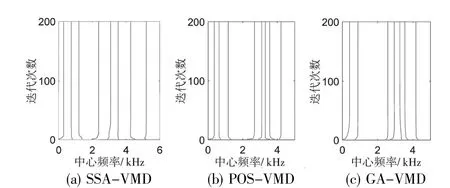
圖4 各算法中心頻率分量對比
綜上可知:SSA-VMD方法在迭代速度、中心頻率分布與所得包絡熵局部最小值方面均優于POSVMD與GA-VMD。
實驗中也得出了不同狀態下的SSA-VMD最優參數,詳細結果如表1所示。

表1 SSA-VMD最優參數
計算各個模態的峭度值,由于峭度值越大,包含沖擊信息越明顯,因此選用峭度值最大的三個IMF分量,計算排列熵與樣本熵。軸承的四種狀態分別對應1、2、3、4的標簽,每種狀態共100個樣本。以此計算故障數據所對應的排列熵[HP1,HP2,HP3]與樣本熵[ES1,ES2,ES3],共同組成特征向量矩陣[HPES]100×6。
診斷模型選用全局搜索能力強、迭代速度快的WOA-SVM[8],將上述三種方法提取到的特征向量輸入到該診斷模型中進行診斷。
令種群數量n=30;迭代次數為200;將K重交叉驗證的準確率稱為訓練準確率,并令其為適應度函數,將已經訓練好的模型上的分類準確率稱為識別準確率,令K=5;在每種數據樣本中隨機選取75組作為訓練樣本,余下25組作為測試樣本。
經實驗,得到POS-VMD、GA-VMD、SSA-VMD三種算法的診斷結果圖,如圖5所示。具體的診斷結果數據如表2所示。
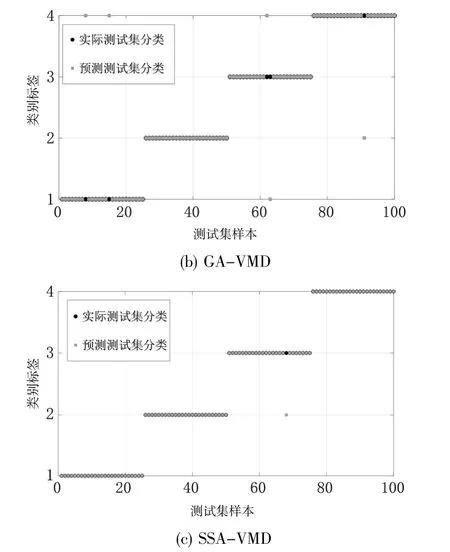
圖5 診斷結果圖
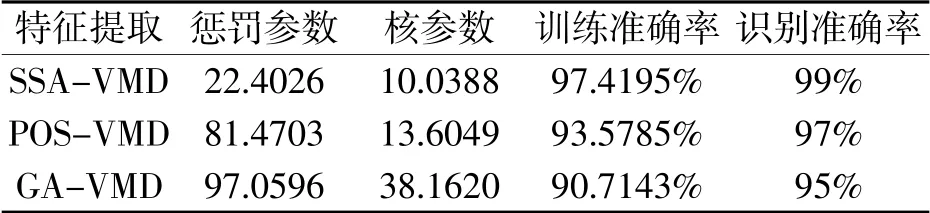
表2 診斷結果數據
可見,與其他兩種方法相比,SSA-VMD的識別準確率與訓練準確率均有所提高。
4 結束語
改進算法基于SSA-VMD和熵的特征提取方法,將包絡熵作為適應度函數,根據峭度篩選IMF分量,選用排列熵與樣本熵共同組成特征向量。通過與POS-VMD和GA-VMD的實驗對比,證明了經SSA-VMD分解后的IMF分量更加清晰、獨立,其尋優速度與尋優結果均更為優越。將三者提取出的特征向量使用同一診斷模型進行分類識別,SSA-VMD的識別準確率與訓練準確率均高于POS-VMD與GA-VMD,表明SSA-VMD和熵相結合的方法能夠更有效的進行特征提取,提高識別準確率。

