基于模糊閾值的小波函數去噪算法

黎道花，周 驊

（貴州大學大數據與信息工程學院，貴陽 550025）

1 引言

小波變換在圖像處理、壓縮和小波去噪等領域應用十分廣泛，但由于不同頻率的時域選取的復雜性，尤其是由于噪聲的存在，使分析變得困難[1-4]。通過將時域與頻域兩個空間單獨分析，會發現噪聲信號往往出現在高頻段內。通過低通濾波器能夠成功過濾高頻段的噪聲信號從而達到去除噪聲的效果。小波包信號去噪主要包括確定分解層、選擇小波包基、量化重構小波系數等步驟[5]。由于分解層、小波包基和閾值的選擇比較困難，使其在實際應用中受到限制。近年來，眾多研究者對此類問題做出研究，如文獻[6]提出一種自適應小波去噪，設置合適的調整參數達到去噪的目的。文獻[7]提出一種新穎的改進符號函數的小波閾值圖像去噪系數，設置不同的調節因子分析圖像中的信噪比變化。文獻[8]提出一種改進的閾值函數，利用調節參數對典型的硬閾值和軟閾值進行自適應調節，其峰值信噪比得到一定程度的改善。

本研究提出的改進算法，便是綜合參考此類現有研究成果，利用硬閾值、軟閾值兩方面的優點，動態地選取閾值，以在圖像處理中得到更加理想的去噪效果。

2 小波變換原理

在小波函數分析中，小波類型主要分為兩類，即DB小波和Harr小波，分別側重于對圖形概貌和圖形細節的分析，其雙尺度方程如下：

式中，n=0,1,2,…。u0(t)則對應正交小波的尺度函數，u1(t)對應小波函數。hk和gk是利用正交小波基的濾波函數。圖像中的混合信號為：

式中，s(t)為正交信號，η(t)為噪聲。通過正交小波包變換，可得各分解層的逼近系數和細節系數。小波包算法通過頻帶的多尺度分解，可以對高頻部分進行重分解，并對某一層小波信號進行重構。

常用閾值函數主要有硬閾值法和軟閾值法，如Stein無偏的似然估計準則、最大最小閾值、固定閾值和啟發式閾值等[9-11]。閾值的選取直接關系到去噪的效果，閾值選擇偏大，會導致圖像細節系數在跳變過程中出現損失或數據包丟失；閾值選取偏小，去噪效果則不明顯，甚至小到近似于連續，沒有跳變過程。目前經常使用Donoho等人基于高斯噪聲模型的去噪法，它是基于獨立正態遍歷的決策理論提出的[12]，表達式為:

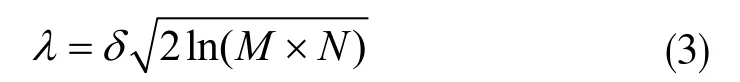
式中，λ為閾值，M×N是圖像的像素，δ為高斯噪聲的方差。

3 改進的模糊閾值算法

現有的小波閾值函數利用高斯噪聲模型進行去噪，是基于獨立正態遍歷決策理論提出的。它在實際中的噪聲無法預知，并且噪聲會均勻地存在于信號的頻帶上。針對這一缺陷，對高斯噪聲進行改進，得到一種模糊噪聲模型，其表達式為：

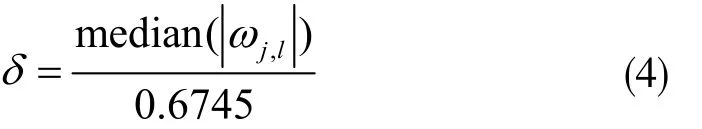
由此可得出新的閾值函數表達式為：

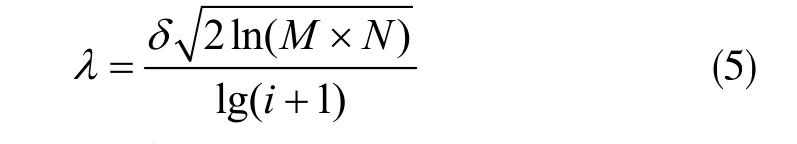
這里，方程中存在了lg(i+1)項，隨著i的增大，閾值函數λ將會降低。小于λ的模糊系數最有可能由噪聲產生，而大于λ的模糊系數最有可能由原始信號產生。

考慮到硬閾值的閾值函數是不連續的，軟閾值具有常偏差，在此基礎上對模糊閾值公式做出改進，取代了硬閾值和軟閾值兩個表達方法，直接合并成一個式子來表達。這也體現出了改進模糊閾值后的自適應性質。同時，通過改進模糊閾值函數而言，整個傳輸過程中的噪聲也會變得越來越小，控制因子也會隨著i值的增加，使閾值函數逐漸變小。

閾值函數中的細節系數包含更多的噪聲，相關函數能夠判斷噪聲背景中的有用信息，因此采用相關分析進行細節系數分析。改進模糊閾值的小波閾值算法的設計流程如圖1所示。

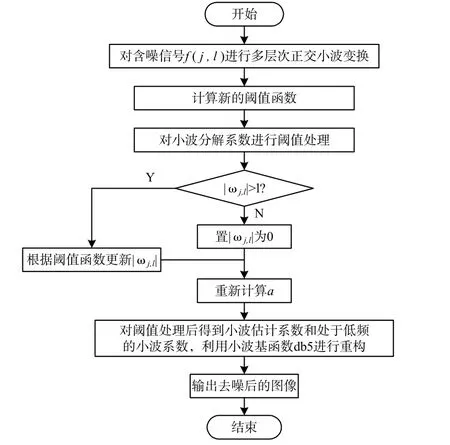
圖1 改進模糊閾值小波去噪算法流程圖

4 實驗及結果分析

為驗證改進模糊閾值的小波函數在圖像處理中的有效性和實用性，以高斯白噪聲下的Lorenz信號為實驗研究對象。正交小波包具有消失矩序和支持集，前者決定了信號的接近能力，當階數越大，分頻效果越好，然而同時也會增加后者的長度和計算量。綜合考慮算法的效果與效率，以db5小波為例進行分析。所有實驗都基于MATLAB 2018a版本上的小波工具箱實現，小波基的分解層數為三層。

先在Lorenz數據中分別加入5%、10%、20%、30%、50%、70%和90%的高斯白噪聲，然后使用db5小波包對污染信號進行分析。以不同噪聲水平下的SNR和RMSE作為指標，對比情況如表1。

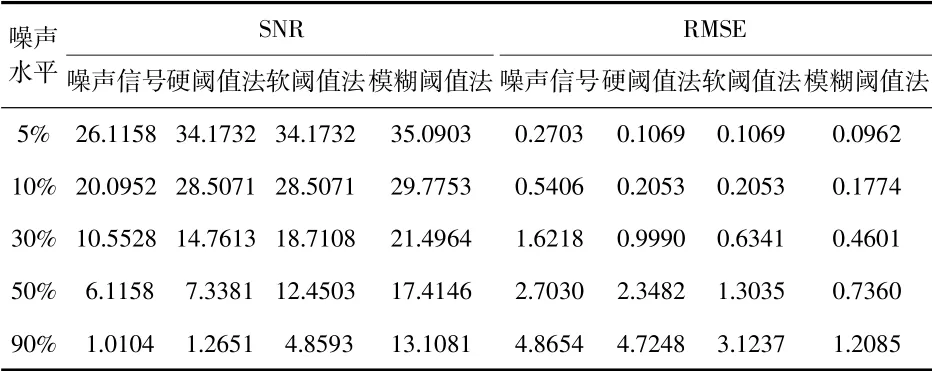
表1 不同噪聲水平下各算法評價指標對比

由表中可見，改進的模糊閾值小波函數具有更好的信噪比，能獲得更好的去噪效果。隨著噪聲水平的逐步增加，SNR會持續降低，但模糊閾值法與其他算法相比仍然具備良好的去噪性能。另外，從RMSE方面來看，模糊閾值去噪法的均方根誤差相對更小，去噪效果更趨穩定。

實驗對上述指標做了進一步的驗證。對不同類型的系數采用奇異值分析、模糊閾值分析和相關性分析。結果表明，改進算法具有廣泛的適用性，對不同噪聲水平的信號去噪都是有效的。噪聲水平越高，該算法去噪效果越好。實驗條件選取噪聲水平20%，得到信號去噪前后的相空間圖和時間序列曲線，以反映不同改進閾值下的小波信號和噪聲情況，實驗結果如圖2所示。

圖2 不同改進閾值的小波信號和噪聲

圖中，經過小波包硬閾值和軟閾值后的信號相空間圖都比較粗糙，部分點偏離了原始軌跡。同時，時間序列曲線在某些地方存在振蕩現象。這主要是由于選擇了固定閾值。相比之下，改進算法不存在這種現象，能更好地反映系統的動態和平滑特性。

為進一步驗證相關系數之間的評價方法，從相關系數方面進行實驗分析，同樣引入硬閾值和軟閾值法的噪聲信號進行實驗對比。在給定延遲時間下，得出信號去噪前后的相關系數和相對偏差，實驗結果如表2。

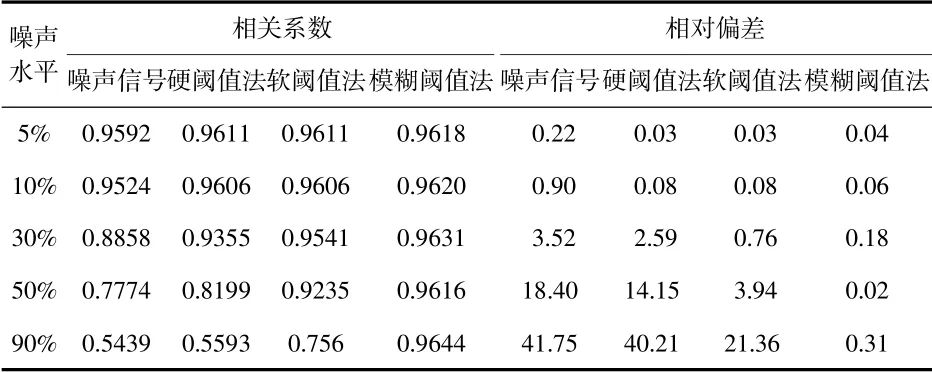
表2 不同噪聲水平下的相關系數對比

通過表中數據對比可知，改進算法去噪信號的相關系數均為高相關。當噪聲水平為70%時，與小波包硬閾值的相關性顯著；當噪聲水平為90%時，與小波包軟閾值的相關性顯著。改進算法的相對偏差也控制在很小的程度，小于0.5%。經過改進算法去噪的信號更接近原始信號的特征，實驗中使用該算法對具體圖像進行處理，處理效果如圖3所示。

圖3 不同去噪方法實驗效果對比

從圖中對比結果可清晰看出，改進的模糊閾值去噪法具有顯著優勢，體現出此方法在圖像處理中的優越性。

5 結束語

改進的模糊閾值去噪算法改善了實際受噪聲影響的信號特性。算法將小波包與奇異性、模糊閾值和相關性的分析結合起來，確定了最優改良方案。通過計算信噪比、均方根誤差、相關系數和功率譜等不同去噪指標，反映出改進去噪算法的優缺點。經實驗驗證，新的算法不僅可以有效降低混沌噪聲，對于具體圖形所做的優化處理，該法也獲得了更為顯著的效果提升，因此具有一定的應用前景。