地面堆載對埋地管道的影響分析
淦 邦,朱 磊,史振龍,董志博
(1.國家管網集團東部原油儲運有限公司,江蘇 徐州 221008;2.中國科學院、水利部成都山地災害與環境研究所,四川 成都 610041; 3.中國科學院大學,北京 100392)
1 概述
油氣管道作為一種線性工程,不免要穿越某些地質狀況復雜的地區,軟土作為一種含水率大、孔隙度大、壓縮性高的特殊土[1],受到荷載或擾動時會對管道產生復雜的摩擦作用,導致管道的破壞[2-5]。其中,地面堆載對軟土地區埋地管道的不良影響是最常見且最容易被忽略的因素,由于以上原因導致的地基不均勻沉降,會使管道產生彎曲變形甚至破裂,并可能引發油氣泄露。如在2017年12月3日,儀長線原油管道大武支線發生焊口撕裂,原油泄漏并進入距離管線斷口處70 m的廢棄灌溉渠內,直接威脅灌溉渠下游的武漢市嚴東湖。
針對地面堆載作用下埋地管道的受力特性,常見的研究方法有現場監測、物理模型試驗和數值模擬[6-9],由于現場監測和物理模型實驗容易受到現場條件的限制,無法針對埋地管道變形的主控因素進行參數敏感性分析,所以亟需通過數值模擬等方式評價外部荷載對管道應力應變的影響方式。如李長俊等[10]利用ANSYS有限元軟件模擬了地表的堆載對埋地管道的影響。帥健等[11]建立了地基-管道三維有限元模型,分析了不同強度地基狀態時地表荷載對管道的影響方式。陳劍健[12]通過結合Boussinesq法和彈性地基梁理論建立了地表荷載作用下的管道力學模型,并采用有限差分法對其求解,計算出地表堆載對埋地管道產生的變形和應力。
本文主要應用ABAQUS有限元軟件,建立了地表堆載作用下管-土相互作用模型,研究了荷載大小、堆載體-管道水平距離、管道埋深以及荷載面積對埋地管道變形及穩定性的影響規律,本文研究結果可為油氣埋地管道的設計與施工提供一定的參考。
2 有限元模型建立
2.1 管道本構模型
由于管道的非線性本構關系,且本文涉及對管道極限荷載狀態的分析,所以本文參照文獻[10]和文獻[13],選取經典的三段式應力應變關系曲線(如圖1所示)作為數值模擬中管道的本構模型。圖1中s1,s2分別為彈塑性變形和塑性變形的起始應力;e1,e2分別為彈塑性變形和塑性變形的起始應變。
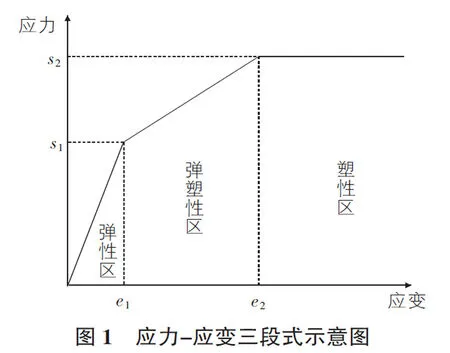
2.2 土體本構模型
本文中土體本構模型選用摩爾-庫侖模型,結合勘察資料設置黏聚力及摩擦角等參數來擬合現場土體工程性質,黏聚力可以體現屈服面的軟、硬化狀態,適用于對外部荷載作用敏感的土體,是一種很好體現巖土體拉壓變形不相等特點的本構模型,已被廣泛應用[14]。
2.3 管土相互作用
管道和管周土體之間存在復雜的相互作用,由于非線性有限元模型的發展[15-19],本文選用表面-表面接觸類型作為模型中管-土接觸模型。由于管道剛度遠大于土體,設置管道外表面為主表面,與管道外表面相接觸的土體表面為從表面。定義管土接觸的切向和法向行為,法向行為選取“硬接觸”,符合管土接觸后可分離的實際情況,切向行為設置摩擦系數為0.5的“罰”函數來定義。
2.4 物理模型及參數
根據輸油鋼管管材技術要求執行標準GB/T 9711—2011石油天然氣工業管道輸送系統用鋼管[20],并對研究區管道參數進行調研,本文數值模型管道采用L320鋼材料為原型,管道外徑D=762 mm,壁厚=8.7 mm,具體材料參數如表1所示。管周土體為黏土,土體模型尺寸為40 m×40 m×8 m,土體尺寸設置為管徑的50余倍,根據圣維南原理滿足邊界條件對管道應力不構成影響,土體底面采用完全固定約束,上表面為自由表面,4個側面則固定住其對應法線方向的運動。按土體表面通過施加一定范圍的均布荷載代替地面堆載。

表1 管道材料參數
3 結果分析
3.1 荷載大小對埋地管道的影響規律
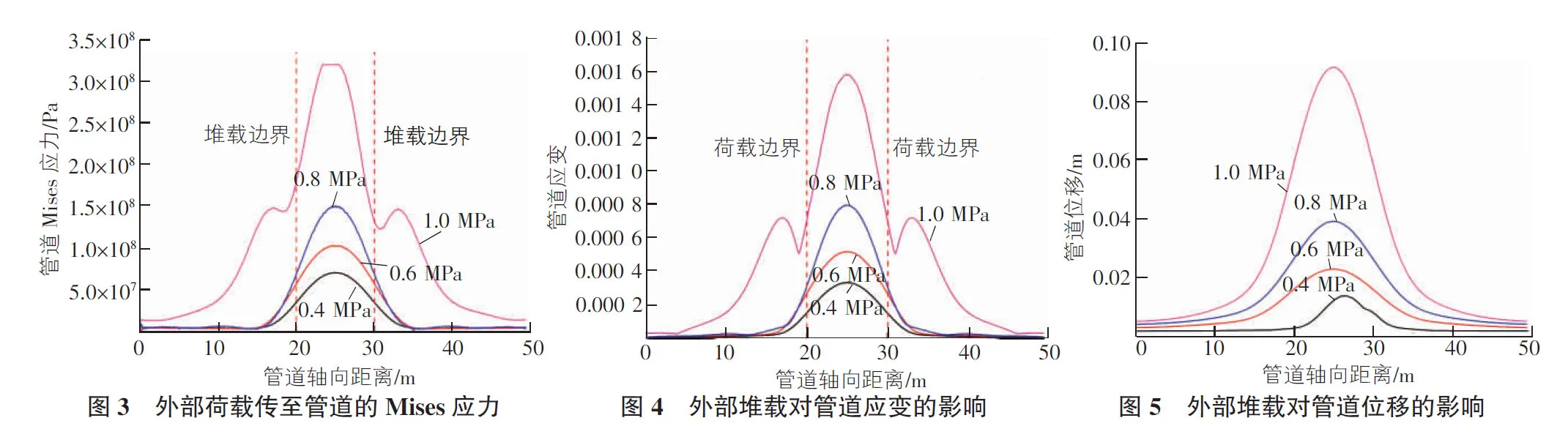
圖2為地表堆載與管道位置關系俯視圖,其中A,B兩點之間的范圍即定義為地表荷載在管道上的投影范圍,A1,B1兩點間距定義為堆載體長度。圖3為外部荷載不同程度時,管道軸向上的Mises應力分布,圖4為受外部荷載影響的管道軸向應變分布。圖3和圖4中顯示,管道應力值隨著外部荷載重量的增加迅速增大;而且位于地表荷載在管道上的投影范圍以內(20 m<管道軸向距離<30 m)的Mises應力值和應變值的增幅要遠大于荷載投影面以外的增幅;同時可以看出,當地表外部荷載的重量達到一定程度時(圖3中為1.0 MPa),地表荷載在管道上的投影范圍外附近(管道軸向距離等于25 m及35 m)所對應的管道Mises應力和應變會稍大于邊界外的一段管道的應力和應變,總體呈現一個“筆架”型的變化趨勢(在圖4中的應變分布圖中,這個趨勢尤為明顯),所以在現場監測中,要重點關注地表荷載在管道上的投影中心所對應的管道點位,也要重視荷載投影邊界所對應的管道位置的力學狀態和變形特征。
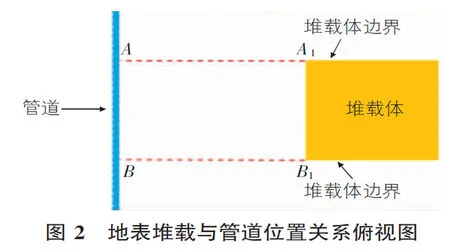
圖5為外部荷載不同程度時,管道軸向上的位移分布。由圖5可知,地表堆載重量越小,堆載體對埋地管道的影響越小,當堆載重量小于一定數值時(本文為0.4 MPa),僅有堆載體投影內所對應的管道受外部堆載影響而產生位移。反之,隨著堆載重量增加,管道位移迅速增大;而且位于荷載在管道上的投影范圍以內(20 m<管道軸向距離<30 m)的位移值的增幅要遠大于投影范圍以外的增幅。
3.2 埋置深度對管道的影響規律
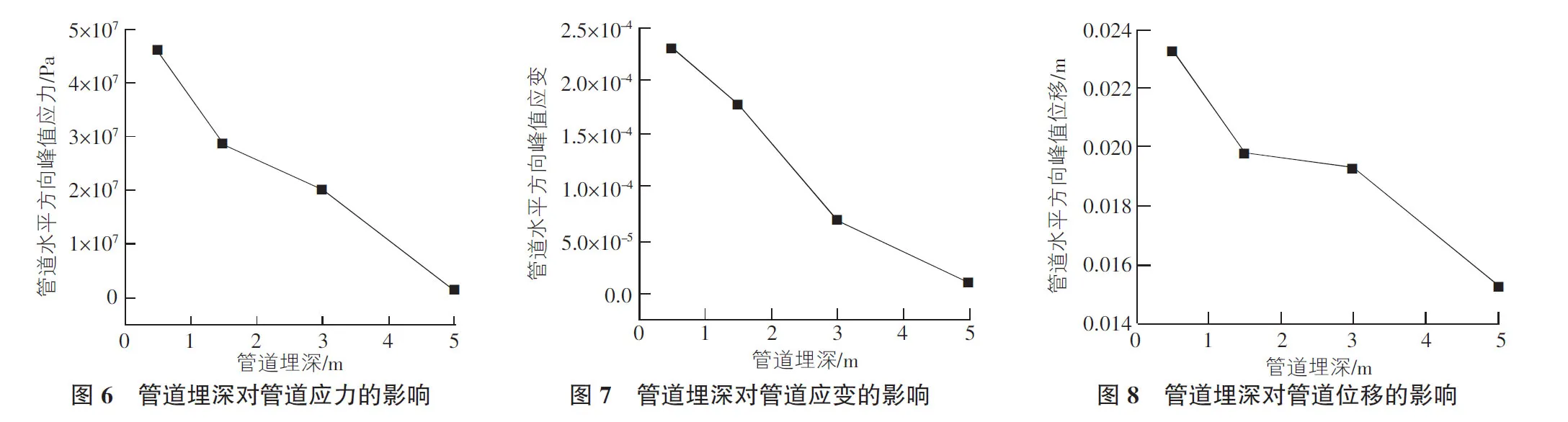
控制地表荷載為0.6 MPa,堆載體-管道間距為5 m,堆載體長度為10 m。圖6~圖8分別表示管道不同埋深下,管道的水平向應力峰值、水平向應變峰值及水平向位移峰值。由圖6~圖8可知,隨著管道埋深的增加,地面荷載對埋地管道的影響越來越小,本文中管道埋深達到5 m時,荷載對管道已無明顯作用。這是由于隨著地面堆載引起的附加應力隨著土體深度的增加逐漸減小,也可理解為隨管道埋深增加,管道遠離地表荷載有效作用區域,從而限制了管道的運動,對管道抵抗變形有利。但這部分只考慮了地表荷載對管道水平方向上應力、應變和位移狀態的影響,并未考慮管道上覆土壓力、孔隙水壓力等的影響,而這些關鍵變量隨管道埋深都可能會對管道應力和變形產生顯著的不利影響,因此并不能簡單的提出,管道埋深越大,管道就越安全的結論。
3.3 堆載距離對管道的影響規律
圖9為堆載體偏離管道中軸線不同程度時,管道軸向的Mises應力分布圖,圖10為管道軸向距離應變分布圖。圖中顯示,應力值和應變值隨堆載體-管道距離的增加而迅速減小,堆載體對埋地管道的影響越小,而且位于載荷投影面以內(20 m<管道軸向距離<30 m)的Mises 應力值和應變值的降幅要遠大于荷載投影面以外的降幅。同時由圖9可以看出,地表荷載導致的管道Mises 應力在間距為2倍荷載長度(A1,B1)時幾乎為0,故在本文中,地表荷載影響長度可以取為荷載長度的2倍,堆載體-管道間距超出這一數值,可認為地表荷載對埋地管道無顯著影響。
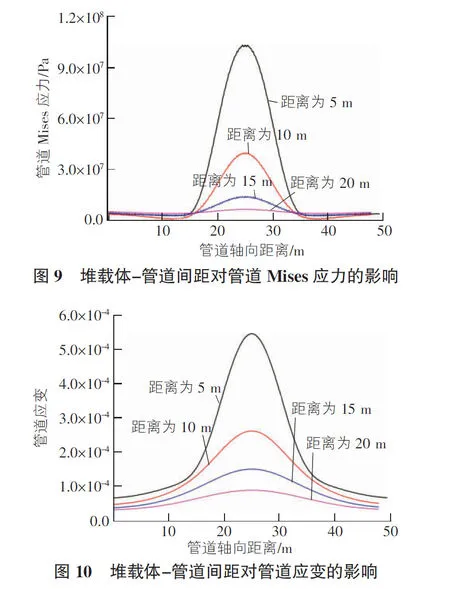
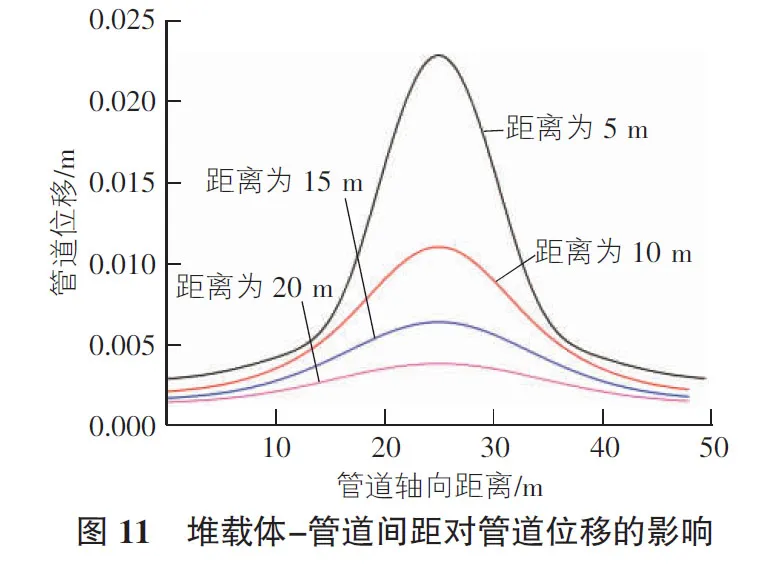
圖11為堆載體偏離管道中軸線不同程度時,管道軸向位移分布圖,從圖11可知,當荷載距離管線軸線位置增加時,管道位移降幅明顯。當間距為2倍荷載長度,即20 m時,管道的最大位移幾乎為0,這是因為地面荷載下方產生一個沉陷區,該沉陷區存在豎向和水平方向的位移,荷載位置移動相當于該沉陷區在移動,隨荷載與管道距離增大,管道遠離沉陷區,管道豎向和水平向位移均減小。
4 結論
應用ABAQUS有限元軟件建立了地表堆載工況下的埋地管道的土體-管道相互作用三維模型,通過數值模擬,研究了堆載重量、管道埋深、堆載體-管道間距對管道力學狀態和變形特征的影響規律。1)管道應力值和變形程度會隨著外部荷載重量的增加而迅速增大,而且位于載荷投影面以內的Mises應力值、應變值和位移的增幅要遠大于荷載投影面以外的增幅。2)管道水平方向應力、應變、位移的峰值隨管道埋深增大而減小,但此時未考慮上覆土體、孔隙水壓力等對管道的作用,不能直接認為管道埋深越深,管道越安全。3)管道應力、應變、位移隨堆載體與管道之間距離的增大而減小。當堆載體與管道間距離超過20 m時,地表堆載幾乎不對管道產生影響。本文針對地表堆載工況下的埋地管道的土體-管道相互作用的研究可以為埋地管道的建設與防護提供一定參考。

