基于剛度定向的工業機器人銑削姿態優化研究

楊 靖 張小儉 吳 毅 葉松濤 嚴思杰， 陸家麟

1.華中科技大學機械科學與工程學院，武漢，4300742.華中科技大學無錫研究院，無錫，2141743.固瑞特模具(太倉)有限公司，蘇州，215488

0 引言

飛機機翼蒙皮、發電機及船用螺旋槳槳葉等大型復雜曲面類零件在國家高端裝備領域廣泛應用。這類零件尺寸大、結構復雜、加工可達性差，傳統數控機床由于加工行程的制約，往往無法適應其制造和裝配需求。相對而言，工業機器人操作空間大、靈活性強，因此機器人加工在航空、航天以及船舶等領域備受青睞。但工業機器人結構剛度較低，銑削加工過程中容易發生顫振，難以保證銑削穩定性。

TOBIAS等[1]和TLUSTY等[2]最早指出，再生效應和模態耦合效應是引起加工顫振的主要機制。由于模態耦合顫振很少發生在剛度較大的數控機床上，故對傳統加工顫振的研究主要聚 焦于鏜桿、銑刀等刀具的再生顫振。與傳統機床不同，串聯結構導致工業機器人剛度較低，使用機器人加工必須考慮模態耦合顫振的影響。近年來，學者們對加工過程中的顫振問題開展了廣泛的研究，但與模態耦合顫振相關的報道較少。GASPARETTO[3]通過建立刀具-工件系統的數學模型，從理論上解釋了模態耦合顫振機理。PAN等[4-5]在機器人銑削實驗中觀察到嚴重的低頻顫振現象，基于動力學模型分析發現切削力方向與工業機器人主剛度方向之間的夾角是影響加工過程穩定性的主要因素，并建立了模態耦合顫振的預測準則?；谇叭说墓ぷ鳎珻EN等[6]將保守同余變換(conservative congruence transformation，CCT)應用到機器人銑削顫振分析中，提出優化機器人進給速度可以避免銑削過程中的模態耦合顫振。雖然以往研究[4-6]表明，改變切削力方向與工業機器人主剛度方向之間的夾角可以抑制顫振，但如何得到工業機器人的主剛度方向報道較少。HE等[7]首次提出了一種將模態振型和工業機器人運動學相結合的剛度定向方法，但需要應用有限元軟件輔助分析。同時，工業機器人的功能冗余特性一直是研究的熱點。學者們定義了不同的冗余優化標準，如剛度性能指標最大化[8]、穩定性邊界最優化[9-10]等，但利用工業機器人功能冗余改變姿態、避免模態耦合顫振的研究未見報道。

本文提出了一種剛度定向方法，利用剛度橢球計算機器人加工系統在切削平面內的主剛度方向，操作過程簡單；針對模態耦合顫振抑制，研究如何利用功能冗余優化工業機器人姿態。

1 機器人銑削模態耦合顫振機理

1.1 機器人銑削動力學建模

為了研究工業機器人銑削過程中的模態耦合顫振，首先建立切削坐標系{c}和主剛度坐標系{k}，如圖1所示。同時，作以下假設[4]來簡化分析：①阻尼效應總是提高系統的穩定性，為了降低復雜度，僅考慮無阻尼系統；②銑削力大小與其他參數無關，只與徑向切削深度成正比。

基于上述假設，在切削坐標系中建立無阻尼二自由度銑削動力學模型：

(1)

x=[xcyc]T

(2)

式中，x為刀尖點在xc和yc方向上的位移；M、K分別為2×2質量和剛度矩陣；Kp為過程剛度矩陣；kp為切削剛度；β為切削力F與xc軸夾角。

本文重點在于研究剛度方向對模態耦合顫振的影響，不失一般性，假設質量矩陣M為對角陣，且對角元素相等。根據ALTINTAS[11]提出的平均銑削力模型，作用在銑刀上進給方向(xc方向)、法向(yc方向)的切削力分量分別為

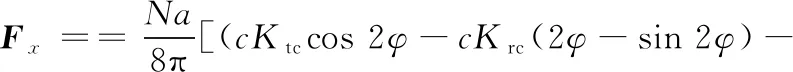
(3)

(4)

式中，N為銑刀齒數；a為軸向切削深度；c為進給率；φ為刀齒的瞬時齒位角；Ktc、Krc分別為切向和徑向切削力的剪切力系數；Kte、Kre分別為刃口力系數；φst、φex分別為刀具的切入角和切出角。

根據式(3)和式(4)給出的切削力分量，可以計算出切削力F與xc軸夾角β，β=arctan(Fy/Fx)。

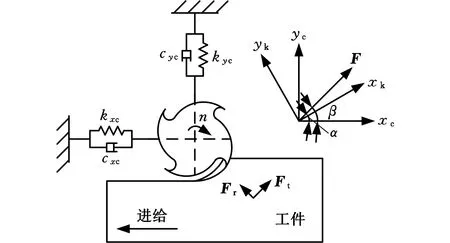
圖1 銑削加工模型Fig.1 Mechanical model of milling

1.2 銑削過程穩定性分析

為了解耦式(1)，需要將其由切削坐標系{c}轉換至主剛度坐標系{k}中。由圖1可知兩個坐標系之間滿足：

(5)

其中，α為xc軸和xk軸之間的夾角。設定：

(6)

將式(5)代入式(1)并對式(1)進行解耦：

(7)

對式(7)進一步計算可得

(8)

其中，mq為模態質量；kx、ky分別為xk和yk方向的模態剛度；γ為切削力F與xk軸夾角，γ=β-α。整理式(8)可得

(9)

記k′x=kx-kpsinαcosγ，k′y=ky-kp·cosαsinγ[5]，則式(9)的特征方程為

(10)

進一步計算可得

(11)

若λ2均為負實數，則加工過程穩定；而當λ2存在虛數時，則產生模態耦合顫振[12]。機器人加工系統的結構剛度kx、ky一般遠大于切削剛度kp，因此，式(11)中的-(k′x+k′y)一定為負數。此時只需要分析式(11)中根號內的部分，即可判定系統穩定性。

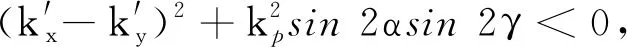
2 機器人加工系統剛度定向方法

2.1 機器人加工系統運動學模型

本文的理論分析及實驗均基于ABB公司的IRB 6660-130/3.1型號工業機器人。進行剛度定向之前，需要對機器人加工系統進行運動學分析。采用修正的D-H方法建立了ABB IRB6660工業機器人的運動學模型，為每個連桿建立坐標系{i}，如圖2所示，其中，坐標系{t}為工具坐標系。基于該運動學模型，可以分析任意連桿之間的位姿關系，獲得工業機器人從基座到末端的齊次變換矩陣T0t，同時計算機器人加工系統的雅可比矩陣。相應坐標系下機器人的D-H參數見表1。

表1 IRB 6660-130/3.1機器人D-H參數

圖2 IRB 6660-130/3.1機器人D-H模型Fig.2 D-H model of the IRB 6660-130/3.1 robot

2.2 剛度定向方法

在銑削加工中，完整的機器人銑削系統包括工業機器人本體、安裝在末端法蘭的電主軸及銑刀。由上文穩定性分析可知：角度α和γ是決定加工過程是否穩定的重要因素。確定這兩個角度需要獲得機器人在加工平面內的主剛度方向，但機器人加工系統的非對稱結構導致其主剛度方向不易確定，因此，本文提出一種基于工業機器人剛度橢球的主剛度定向方法。機器人末端剛度橢球作為評價機器人在整個笛卡兒空間內的綜合剛度性能指標，其各個方向上的軸長直接反映了機器人末端在對應方向上的剛度，因此通過計算剛度橢球在切削平面內的長軸和短軸方向，即可確定工業機器人主剛度方向。具體步驟如下：

剝奪他人生命的形式有很多種，法律對具體的行為方式不做限制。既可以暴力手段，也可以是非暴力手段；既可以是作為方式，也可以是不作為方式。[4]10-11因艾滋病的病情的特殊性，故意傳播艾滋病符合故意殺人罪的客體特征。

(1)進行工業機器人關節剛度辨識實驗[13]，求出其關節空間剛度矩陣Kθ，并通過矩陣Kθ與末端笛卡兒空間剛度矩陣K之間的映射關系，獲得機器人笛卡兒剛度矩陣K。

(2)利用剛度矩陣K中的力-線位移子矩陣Kft(3×3)計算出機器人加工系統末端的剛度橢球，并將其在切削坐標系中表示。

(3)剛度橢球與切削平面相交面為橢圓面，通過求取該橢圓長軸及短軸方向，即可獲得機器人加工系統在特定位姿下，切削平面內的最大剛度方向和最小剛度方向。

通過實驗得到的工業機器人各關節剛度值見表2。在關節空間中，每個關節的剛度是相互獨立的。

表2 IRB6660機器人關節剛度

通過雅可比矩陣將關節剛度矩陣轉化至笛卡兒空間[14]：

K=J-TKθJ-1

(12)

其中，J為相對切削坐標系{c}表示的雅可比矩陣；Kθ為關節空間剛度矩陣，Kθ=diag(Kθ1，Kθ2，…，Kθ6)；K為6×6笛卡兒空間剛度矩陣，可以將其劃分成4個3×3子矩陣：

(13)

式中，Kft、Kfr、Kmt、Kmr分別為力-線位移子矩陣、力-角位移子矩陣、力矩-線位移子矩陣和力矩-角位移子矩陣。

圖3 機器人加工系統末端剛度橢球Fig.3 The stiffness ellipsoid of the end of roboticmachining system

該笛卡兒剛度橢球在自身坐標系{e}中的方程可表示為

(14)

橢球坐標系{e}相對于切削坐標系{c}的齊次變換矩陣Tce用剛度橢球的特征向量可表示為

(15)

式中，Rce為兩坐標系的旋轉矩陣。

因此，橢球面上的任意一點q在橢球坐標系中的坐標qe=(xe,ye,ze)與在切削坐標系中的坐標qc=(xc,yc,zc)滿足：

(16)

式中，μij(i,j= 1, 2, 3)為特征向量μi各分量。

將式(16)代入式(14)，可得剛度橢球在切削坐標系中的方程：

(17)

則剛度橢球與切削平面的橢圓交面方程為

(18)

此時，橢圓的主軸方向即為機器人加工系統在切削平面內的主剛度方向，如圖4所示，橢圓主軸方向可根據橢圓方程進一步求出。

圖4 機器人加工系統主剛度方向Fig.4 The principle stiffness directions of robotic machining system

3 工業機器人銑削姿態優化算法

3.1 機器人功能冗余特性

六自由度工業機器人在銑削應用中，只需要五個自由度即可確定刀具位姿，其中三個自由度用于定位刀具中心點，另外兩個自由度用于確定刀具軸線的方向，從而產生一個冗余自由度。這種特性被稱為功能冗余，增加了工業機器人在執行任務時可達空間的體積和末端執行器的靈活性。如圖5所示，改變機器人姿態，使得刀具坐標系{t}繞zt軸旋轉角度θr，此時兩個不同機器人姿態下的刀尖點位置和刀具軸向相同。這意味著對于同一加工軌跡，可以用工業機器人的不同位形進行加工，從而為優化姿態抑制模態耦合顫振提供了可能。本文用旋轉角度θr表示冗余自由度，對于特定的刀具位姿，θr可以指定為在機器人可達范圍內的任何值。

角度θr給定后，根據第2.1節確定的機器人D-H參數可以計算出任意加工位置處刀具坐標系相對于基坐標系的齊次變換矩陣T0t：

(19)

其中，Pi(i=x，y，z)表示刀具坐標系原點在機器人基坐標系中的位置分量。通過逆運動學求解即可推導出機器人各關節角度，從而確定各冗余角θr對應的機器人銑削姿態。

3.2 姿態優化算法

基于工業機器人功能冗余特性及所提的剛度定向方法，機器人銑削姿態優化算法如圖6所示。首先，給定初始冗余角θr=0°，變化范圍為0°～360°，并設定角度增量dθ。給定θr后，即可獲得齊次變換矩陣T0t，通過逆運動學求解計算出機器人各關節角度；然后求取該機器人姿態下的笛卡兒空間剛度矩陣K，并推導出相應的剛度橢球，其與切削平面的交面為橢圓。通過計算該橢圓長軸及短軸方向，得到加工平面內的主剛度方向，從而確定角度α和角度γ。最后，基于模態耦合顫振穩定性判據，判斷加工過程是否穩定。基本步驟總結如下：①確定初始冗余角θr，設定角增量dθ，并計算機器人各關節角度；②執行2.2節提出的剛度定向過程，得到切削平面內的主剛度方向；③根據1.2節建立的模態耦合顫振準則，判斷機器人銑削的穩定性；④重復上述步驟，遍歷所有θr，并檢測邊界，確定銑削過程穩定的機器人姿態。

圖6 機器人銑削姿態優化算法流程圖Fig.6 Flowchart of posture optimization algorithm for robotic milling

4 案例分析

4.1 機器人銑削實驗

實驗裝置如圖7所示，通過將電機主軸連接到六軸工業機器人(IRB6660)的末端，搭建了機器人銑削實驗平臺。采用直徑12 mm、螺旋角30°、刃長30 mm的硬質合金四刃立銑刀，在Q235結構鋼工件(50×100 mm)上進行了平面銑削實驗。通過單軸加速度傳感器(3711F11100G，PCB)采集銑削過程中機器人的振動加速度信號。

為了驗證利用冗余自由度優化機器人姿態避免模態耦合顫振的可行性，在兩個位置分別進行半槽銑削實驗和全槽銑削實驗，刀尖點在兩個位置處的坐標分別為(1050，-1500，875)mm、(1350，-1500，875)mm(相對于機器人基坐標系)。每組銑削實驗分別在機器人12個不同位形下進行。所有實驗的切削參數均為：軸向切深ap=0.3 mm，進給速度f=16 mm/s，主軸轉速n=2400 r/min，銑削方式為順銑。

圖7 銑削實驗裝置Fig.7 Milling test equipment

4.2 結果和討論

利用2.2節提出的剛度定向方法，計算出機器人銑削系統在位置1和位置2處不同位形下的主剛度方向。部分冗余角θr對應的機器人關節角θ1～θ6與角度α見表3。

表3 機器人關節角及主剛度方向角

根據1.2節建立的模態耦合顫振模型，位置1和位置2處的潛在顫振區域如圖8中的陰影部分所示，當平均銑削力位于圖8中的陰影部分時，可能發生模態耦合顫振。由式(3)和式(4)計算出半槽銑削和全槽銑削時，平均銑削力F與xc軸夾角β分別為94°和127°。將角增量dθ設定為10°，通過3.2節提出的姿態優化算法，可以判斷采用不同冗余角θr對應的機器人姿態進行銑削時是否發生模態耦合顫振，預測結果如圖9所示。由圖9可知，機器人在位置1和位置2處進行半槽銑削時，所有位形下均不會發生模態耦合顫振；對于全槽銑削，在位置1處，冗余角θr為70°～170°時，銑削過程穩定；而在位置2處，穩定的冗余角范圍擴大至0°～170°。

(a)位置1 (b)位置2圖8 潛在顫振區域示意圖Fig.8 Diagram of potential chatter area

圖9 不同冗余角θr的穩定性預測結果Fig.9 Stability prediction respect to functional redundancy θr

為減少實驗工作量，實驗時設定角增量dθ=20°，采用機器人12個不同的典型位形在位置1和位置2處分別進行半槽銑削和全槽銑削實驗，實驗采用的冗余角如圖9所示，并通過低頻加速度計采集機器人振動信號。為了進一步分析實驗結果，對銑削過程中的加速度信號進行快速傅里葉變換(fast fourier transform，FFT)。圖10～圖12所示為部分典型實驗結果。

在位置1處進行全槽銑削時，為了尋找過渡冗余角邊界，增加θr=70°的實驗。如圖10a～圖10c所示，機器人在冗余角θr=0°、40°對應的位形下銑削時出現了明顯的低頻顫振頻率(～7 Hz)，通過模態錘擊實驗，確定該頻率接近機械臂的低階固有頻率(～7.74 Hz)，且在13個不同位形下，機械臂固有頻率變化很小(7～8 Hz)；當冗余角達到70°時，7 Hz左右對應的幅值明顯降低；而在冗余角θr=80°、120°、140°時，如圖10d～圖10f所示，7 Hz左右的顫振頻率消失，說明銑削過程中沒有發生模態耦合顫振，與預測結果一致。

(a)θr=0° (b)θr=40°

(c)θr=70° (d)θr=80°

(e)θr=120° (f)θr=140°圖10 位置1處全槽銑削加速度信號頻譜Fig.10 Acceleration signal spectrum of full-slot milling at position 1

在位置1處進行半槽銑削實驗，實驗結果顯示所有冗余角下銑削過程均穩定，符合預測結果，加速度信號快速傅里葉變換的典型結果如圖11所示，機器人在冗余角θr=0°、40°對應的姿態下銑削時并沒有出現7 Hz左右的峰值，與全槽銑削結果對比明顯，這是因為半槽銑削時，平均銑削力更加靠近y軸，從而遠離了顫振區域；在位置2處進行的半槽銑削實驗同樣符合預測結果，在所有冗余角下均穩定。

(a)θr=0° (b)θr=40°圖11 位置1處半槽銑削加速度信號頻譜Fig.11 Acceleration signal spectrum of half-slot milling at position 1

位置2與位置1相比，x坐標變化0.3 m。通過模態錘擊實驗，12個不同位形下的機器人低階固有頻率均為8.5 Hz左右。由預測結果可知，位置2處全槽銑削時穩定的冗余角范圍相比位置1擴大至0°～170°。對比表3中兩個位置處的α角，位置2處各冗余角θr對應的α角的絕對值相對位置1均有所增大，這意味著位置2處的不穩定區域相比位置1逆時針旋轉，如圖8所示；而兩個位置處平均銑削力的方向角β相同，所以位置1處不穩定的冗余角范圍0°～70°在位置2處變得穩定，θr=0°、40°的實驗結果如圖12所示。

(a)θr=0°

(b)θr=40°圖12 位置2處全槽銑削加速度信號頻譜Fig.12 Acceleration signal spectrum of full-slot milling at position 2

5 結語

實驗結果表明，當使用優化后的機器人姿態進行銑削時，低頻模態耦合顫振被顯著抑制。與以往方法不同，本文方法不需要改變刀具進給方向、工件方向或切削參數，從而保留了機器人銑削的靈活性，使得機器人加工的工業應用范圍更廣泛。