基于變彈性模量的Ti-6Al-4V板材五點彎曲回彈預測

屈 聰 孟智娟 趙 亮 陳 耀 馬立東

太原科技大學機械工程學院，太原，030000

0 引言

Ti-6Al-4V鈦合金具有質量小、強度高、耐腐蝕和耐疲勞等優越的性能，在航空、軍事、醫學等[1-3]領域得到了廣泛的應用。但因其具有較高的屈服強度和較低的彈性模量，使得Ti-6Al-4V在彎曲成形過程中的回彈難以控制，所以預測彎曲回彈對產品質量具有重要的意義。國內學者在彎曲回彈理論方面做了大量研究。趙軍等[4]建立了平面彎曲彈復方程，并將其成功地應用于擴徑矯圓工藝。在此基礎上，ZHAO等[5-6]對大型管道的管端整修過程中回彈的預測和控制進行了研究，并通過預緊力和彎矩的加載方法對型材平面拉伸彎曲的回彈分析進行了研究。段永川等[7]建立了V形小曲率自由彎曲回彈的解析預測模型，利用此模型分析了不同工藝參數對V形自由彎曲力和回彈后彎曲角度的影響規律，確定了彎曲力和回彈角的主要影響因素。馬瑞等[8]針對板材回彈問題，建立了迭代補償機制，并將此工藝應用于寬板自由彎曲工藝的回彈控制，根據每次實驗的回彈量，迭代補償機制可以預測下一次的補償值。李佼佼等[9]建立了三點彎曲有限元模型，研究了不同厚度、不同溫度下Invar30合金厚板的回彈規律。MA等[10]分析了ERW管FFX預制段的五點彎曲過程和回彈過程，建立了五點彎曲回彈力學模型。吳義江等[11]以高強鋼厚板冷彎成形為研究對象，利用數值仿真方法對回彈的影響參數進行了分析。

目前有很多學者使用有限元模擬的形式來預測成形過程中的回彈。有限元模擬與實際情況也存在一定的誤差，這與所構建的模型、單元的劃分、材料本構設置、邊界條件設置等都有關系，其中材料本構模型尤為重要。BARLAT等[12]提出了一個各向異性屈服準則，適用于平面應力條件，能夠描述板料變形時的面內各向異性。BARLAT等[13]又提出了YLD2000-2D屈服準則并應用于鋁合金板材成形過程有限元分析中。NAOFAL等[14]基于Y-U硬化模型及變彈性模量對板材輥彎成形過程回彈預測進行了研究，結果表明，硬化模型及彈性模量變化對回彈預測有很大的影響。FU等[15]針對彎曲成形過程中的回彈問題，利用遺傳算法優化權值進而實現理想的彎曲回彈預測和研究。BADR等[16-18]對Ti-6Al-4V鈦合金室溫輥彎成形進行了研究，提出了一種各向異性的彈塑性本構材料模型，該模型在預測室溫下Ti-6Al-4V薄板樣品的鮑辛格效應和瞬態硬化行為方面具有更高的準確性，在此基礎上他們還研究了輥彎成形方式對Ti-6Al-4V室溫輥彎成形回彈的影響。

隨著科學技術的進步與制造業的不斷發展，人們對回彈預測的精度提出了更高的要求。彈性模量在成形過程中發生變化，從而影響回彈預測的精度，這在回彈問題的研究領域是一個新的研究方向。MORESTIN等[19]通過實驗發現，當塑性應變僅為5%時，彈性模量降幅即可達到初始值的10%以上，并且通過所開發的軟件計算了沖壓工藝中的回彈，該軟件考慮了彈性模量的變化，計算結果很接近實驗值。YOSHIDA等[20]針對高強鋼DP590的材料性能進行了研究，發現當增加預應變時彈性模量出現迅速下降的趨勢，并提出了Y-U硬化模型及變彈性模量數學模型。LIU等[21]以超高強鋼為研究對象，提出了一種考慮彈性模量變化的數學模型，并將其應用于三維有限元分析(finite element analysis,FEA)中來模擬冷軋成形過程，通過與Swift材料本構模型的對比，使用非線性彈性模量計算出的回彈精度提高了18%。SUN 等[22]針對材料的彎曲回彈行為，建立了QPE模型用來描述彈性模量的非線性變化，該模型提高了彎曲回彈的預測精度。

本文以Ti-6Al-4V鈦合金為研究對象，通過單軸拉伸實驗與循環加載-卸載實驗確定了材料各向異性參數并研究材料五點彎曲變形過程中彈性模量變化規律, 建立了變彈性模量數學模型。基于變彈性模量數學模型及YLD2000-2D屈服準則編寫了材料本構模型子程序，利用ABAQUS仿真軟件Umat子程序接口將自定義本構模型嵌入有限元模型中，進行了常溫下板材五點彎曲回彈數值模型。最后，進行了常溫下五點彎曲實驗，對比分析了實驗結果與模擬結果。

1 材料選取

鈦是一種同素異構體，有兩種不同的晶體結構，在低于882℃時稱為α-Ti，在882℃以上時稱為β-Ti，α-Ti為理想的密排六方(HCP)結構，β-Ti呈體心立方晶體結構。Ti-6Al-4V鈦合金作為一種具有α+β兩相的等軸組織合金，具有良好的綜合性能，可以較好地進行熱應力加工，也能通過淬火、時效處理使合金強化,其主要構成元素及含量見表1。

表1 材料化學成分(質量分數)

2 實驗、數值模擬及本構模型的建立

2.1 單軸拉伸、循環加載-卸載實驗

Ti-6Al-4V鈦合金材料具有較強的各向異性，為測定Ti-6Al-4V鈦合金的材料性能及各向異性系數，進行了準靜態單軸拉伸實驗。如圖1所示，該實驗在Instron-5969萬能材料實驗機(載荷50 kN)上進行。

圖1 Instron-5969萬能材料實驗機Fig.1 Instron-5969 universal material testing machine

分別在材料的RD(軋制方向)、DD(對角線方向)、TD(橫向)三個方向進行了拉伸實驗。根據實驗需求，制作了拉伸試樣，試樣尺寸及取樣方式如圖2和圖3所示。本實驗在常溫下進行，拉伸速率為0.01 mm/min，使用接觸式引伸計測量變形。

(a)拉伸試樣示意圖

(b)拉伸試樣實物圖圖2 拉伸試樣的尺寸Fig.2 The size of the tensile specimen

圖3 取樣方式Fig.3 Sampling method

為測定Ti-6Al-4V鈦合金在不同塑性應變下彈性模量的變化規律，對其進行了單軸循環加載-卸載實驗。該實驗同樣在Instron-5969萬能材料試驗機上進行，實驗條件及拉伸試樣與單軸準靜態拉伸實驗相同。單軸循環加載-卸載實驗的具體實驗步驟如下：將試樣加載至所需的初始預應變，停止拉伸，之后將應力卸載為0；再加載至第二個預應變值，停止拉伸，將應力卸載為0，如此循環直到完成最大的預設應變值。預應變設置為：0.8%、1.0%、1.5%、2%、2.5%、3.3%、4.1%、5.1%、6.1%、7.1%、8.1%、9.1%。同理，對RD、DD、TD三個方向的試樣進行測試。與其他兩個方向相比，TD方向的延伸率較低，為了防止接觸式引伸計被損壞，TD方向的試樣預應變值僅設置到7.1%。

(a)RD方向的應力-應變曲線

(b)DD方向的應力-應變曲線

(c)TD方向的應力-應變曲線圖4 加卸載實驗應力-應變曲線Fig.4 Loading-unloading-loading experiment stress-strain curves

2.2 實驗結果分析

循環加載-卸載實驗所測得RD、DD、TD三個方向的應力應變曲線如圖4所示。通過單軸準靜態拉伸實驗得到了Ti-6Al-4V鈦合金RD、DD、TD三個方向的應力-應變曲線，如圖5所示。

圖5 Ti-6Al-4V鈦合金應力-應變曲線Fig.5 Ti-6Al-4V titanium alloy stress-strain curves

本實驗測量的Ti-6Al-4V鈦合金RD、DD、TD三個方向的彈性模量、0.2%偏移屈服強度、極限抗拉強度、總伸長率和塑性應變比(r值)見表2。

表2 Ti-6Al-4V鈦合金單軸拉伸實驗的材料參數

r值按以下公式計算：

(1)

式中，εw、εt分別為寬度方向和厚度方向上的應變；w0、w分別為試樣的初始寬度和最終寬度；t0、t分別為試樣的初始厚度和最終厚度。

2.3 變彈性模量的定義

彈性模量的值在一般的應力-應變曲線中為直線的斜率，由上文單軸循環加載-卸載實驗數據可以發現,重新加載的彈性模量具有遲滯特性，彈性模量不能再以簡單的取斜率的方式來計算，故一些學者提出了三種彈性模量的計算方式：加載模量、卸載模量、弦線模量。其中，加載模量為二次加載曲線前半段連線的斜率,卸載模量為卸載曲線前半段連線的斜率,弦線模量為前一次最大應變點與后一次起始應變點連線的斜率。NAOFAL等[14]驗證了弦線模量比加載模量與卸載模量對預測回彈具有更高的精度,故本文選取弦線模量的計算方式計算加載-卸載曲線中的彈性模量值。弦線模量的計算公式如下：

(2)

式中，σ1、ε1分別為前一次最大應變點的應力、應變值；σ0、ε0分別為后一次起始應變點的應力、應變值。

基于YOSHIDA等[20]提出的變彈性模量數學模型，對以上三個方向的數據點進行擬合。變彈性模量數學模型如下：

(3)

式中，E0為初始彈性模量；Eav為變形過程中平均彈性模量；Ea為材料參數；ξ為控制彈性模量下降速率的材料參數。

基于以上公式，擬合得到三個方向的變彈性模量公式參數，其中每個方向的參數E0、Ea、ξ見表3。

表3 變彈性模量數學模型參數

圖6 RD、DD、TD方向的變彈性模量擬合曲線Fig.6 Variable elastic modulus fitting curve for RD, DD, TD

圖6為實驗數據點與擬合曲線的對比圖。RD、DD、TD三個方向的彈性模量隨著塑性應變的增加都出現了明顯的下降趨勢。在3.3%塑性應變之前，彈性模量下降速率較快，而在3.3%塑性應變之后，該下降趨勢逐漸趨于平緩，最終成為一個定值。Ti-6Al-4V鈦合金的塑性應變為8.3%時，RD方向彈性模量下降了18.9%，DD方向彈性模量下降了22.39%，TD方向彈性模量下降了20%。從圖6中可以看出,根據數學模型擬合的曲線與實驗數據非常接近，說明數學模型可以很好地描述材料彈性模量變化規律。雖然Ti-6Al-4V鈦合金三個方向的變化規律相同，但由于初始彈性模量存在一定的各向異性，導致在整個變形過程中RD方向的彈性模量始終大于另外兩個方向的彈性模量，在較大塑性應變下的彈性模量比另外兩個方向的彈性模量大10 GPa左右。由于DD方向和TD方向的初始彈性模量相近，并且隨著塑性應變增加，它們的彈性模量的變化規律相同，故DD、TD兩個方向的彈性模量在變形過程中比較接近。

2.4 YLD2000-2D屈服準則

由于Ti-6Al-4V鈦合金在成形過程中表現出較強的各向異性，各向同性屈服準則并不適用，所以本文采用文獻[13]中的YLD2000-2D屈服準則。YLD2000-2D屈服準則是建立在平面應力基礎上的一個平面屈服準則，它是通過在Cauchy應力張量上使用兩個線性變換將材料的各向異性參數引入屈服函數當中。YLD2000-2D屈服準則可以很好地描述Ti-6Al-4V鈦合金的屈服行為，且對研究薄板五點彎曲過程(可近似看成二維問題)也非常適用。YLD2000-2D屈服函數表達式如下：

(4)

φ′=|X′1-X′2|a

(5)

φ″=|2X″2+X″1|a+|2X″1+X″2|a

(6)

其中，X′1、X′2，X″1、X″2分別為X′和X″的應力主值，即

(7)

(8)

X′和X″的分量可以通過以下兩個線性變換獲得：

X′=C′s=C′Tσ=L′σ

(9)

X″=C″s=C″Tσ=L″σ

(10)

(11)

其中，變換矩陣T的作用是將柯西應力σ變換為其對應的偏應力張量s；矩陣C′與C″的作用是引入各向異性參數。即

(12)

(13)

(14)

(15)

(16)

(17)

其中，α1～α8為8個各向異性參數，當這8個參數的值等于1時，該屈服準則就變成了各向同性屈服準則。這8個參數需要通過單軸拉伸實驗以及雙軸拉伸實驗所測得的σ0、σ45、σ90、σb、r0、r45、r90、rb這8個實驗數據計算得出，其中，σb、rb由文獻[16]給出，其他參數具體計算方式參考文獻[13]，各向異性參數取值見表4。

表4 YLD2000-2D各向異性參數

2.5 數值模擬

本文采用ABAQUS有限元軟件對常溫下Ti-6Al-4V鈦合金板材五點彎曲過程進行數值模擬。數值模擬共分為兩組，分別對應不同的壓彎行程y=25 mm，30 mm。模型尺寸及彎曲行程示意圖見圖7。此數值模擬共分為以下3個分析步：①上模具與板材上層接觸；②壓彎至指定位置；③上模具上升板材回彈。

圖7 模具尺寸及彎曲行程示意圖Fig.7 Schematic diagram of mold size and bending stroke

Ti-6Al-4V鈦合金板材五點彎曲有限元模擬三維模型如圖8所示。Ti-6Al-4V鈦合金板材長330 mm，寬40 mm，厚度2 mm，上模具、底輥模具和下輥模具均設置為離散剛體，板材設置為可變形殼體。

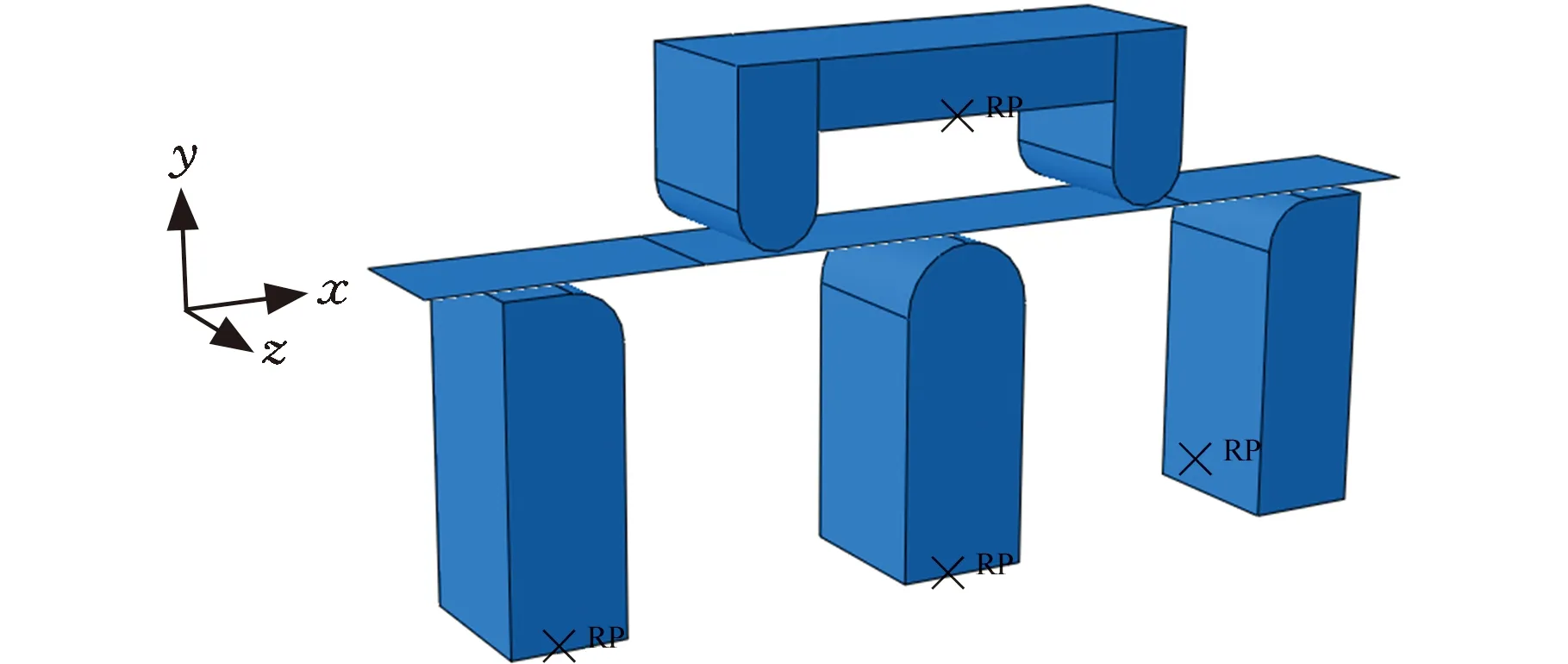
圖8 有限元模型Fig.8 Finite element model

ABAQUS具有高度的開放性，當 ABAQUS 材料庫中包含的現有本構模型中不能準確地表示要模擬的材料行為時，它為用戶提供了自定義材料模型子程序接口，即Umat子程序接口。本文基于以上YLD2000-2D屈服準則及變彈性模量數學模型建立了Ti-6Al-4V鈦合金材料本構模型，并通過Umat子程序接口將該模型嵌入ABAQUS軟件中。為研究屈服準則及變彈性模量對Ti-6Al-4V板材彎曲回彈預測的影響，本文進行了兩種不同本構模型情況下的彎曲回彈模擬。

為了準確描述Ti-6Al-4V鈦合金的硬化曲線，本文選擇Voce模型來描述其流動應力的變化。對軋制方向的流動應力進行了擬合，擬合結果如下：

(18)

數值模擬中，兩種本構模型的材料參數設置見表5。

表5 兩種本構模型的輸入參數

ABAQUS中對模型進行網格劃分是決定精度高低的重要環節。網格劃分的粗細程度和單元類型的選擇都在不同程度上影響著最終的計算結果。YLD2000-2D是基于平面應力狀態下的屈服準則，對此板材單元采用S4R四節點殼單元。為了使計算結果的準確度更高，將板材分成兩個區域分別設置不同的單元尺寸，其中,變形大的區域網格較精細，變形小的區域網格較粗糙，網格劃分如圖9所示。

圖9 單元劃分法Fig.9 Element division method

在接觸面設置中，選擇面對面接觸作為板材與模具之間的接觸類型，并且遵循主從面選擇，其中定義剛體面為主面，可變形體面為從面。此外對兩個面之間的接觸定義接觸屬性，其中,法向屬性設置為“硬接觸”，切向屬性設置為庫侖摩擦，設定摩擦因數為0.2。對于邊界條件的設置，上下模具需設置參考點，如圖8中的RP。下輥和底輥模具在參考點處設置完全固定約束，上模具在參考點處設置y軸方向的位移載荷。

Ti-6Al-4V鈦合金由于其彈性模量小，在彎曲的過程中會產生很明顯的回彈現象。圖10、圖11分別為基于子程序本構模型和ABAQUS原有本構模型計算的板材彎曲行程30 mm狀態下的橫向彈性應變圖，可以看出Ti-6Al-4V鈦合金板材在卸載后發生了很明顯的回彈。在彎曲過程中，發生彈性變形的區域主要集中在板材的中間區域，且在回彈之后彈性應變全部恢復。

(a)回彈前

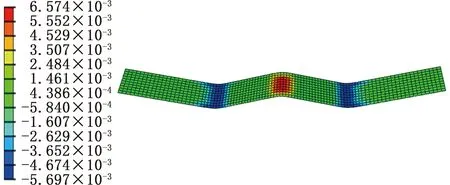
(b)回彈后圖10 彎曲行程為30 mm時基于子程序計算的橫向彈性應變云圖Fig.10 Transverse elastic strain nephogram based on subroutine calculation when bending stroke is 30 mm

(a)回彈前

(b)回彈后圖11 彎曲行程為30 mm時基于原有材料模型計算的橫向彈性應變云圖Fig.11 Transverse elastic strain nephogram based on original material model when bending stroke is 30 mm

2.6 常溫下五點彎曲實驗

為驗證數值模擬結果的準確性，進行了常溫下Ti-6Al-4V鈦合金板材五點彎曲實驗，本實驗在電子萬能實驗機上進行。如圖12所示，先將上模具與板材上表面貼合，之后在操作系統中設置壓下量，上模具壓下至指定的壓下量，最后上模具抬升。實驗所用模具如圖12所示，分為上模具、下輥模具、底輥模具，模具尺寸與數值模擬中模具的尺寸完全相同。實驗所用的Ti-6Al-4V鈦合金板材幾何參數為330 mm×40 mm×2 mm，板材是以初軋或鍛造的板坯為原料經加熱、軋制、熱矯、熱處理、中斷、矯形、除磷、酸洗等基本生產過程加工而來的，其中熱處理為硬退火。

(a)板材與模具貼合圖

(b)板材壓彎圖圖12 五點彎曲實驗工藝流程圖Fig.12 Process flow chart of five point bending test

本實驗中，壓下量分別取25 mm和30 mm，實驗測得的板材回彈后與水平線夾角θ的示意圖見圖13。夾角θ的實驗數據見表6。

圖13 夾角θ的示意圖Fig.13 Schematic diagram of included angle θ

表6 不同彎曲行程下板材回彈后與水平線夾角

為了使結果更有說服性，取三次實驗的平均值作為后續分析的依據。當壓彎行程為25 mm時，板材回彈后與水平線夾角取6.51°；當壓彎行程為30 mm時，夾角取11.12°。

3 回彈分析

通過常溫下的數值模擬及彎曲實驗獲知了Ti-6Al-4V鈦合金板材在不同壓彎行程及不同本構模型下的板材回彈情況。不同本構模型對Ti-6Al-4V鈦合金板材五點彎曲回彈預測的影響如圖14所示(示意圖為板材的左半部分)。圖14展示了25 mm和30 mm兩種不同彎曲行程下不同本構模型對板材最終彎曲成形效果的影響。彎曲行程相同的情況下，基于Mises各向同性本構模型得到的數值模擬結果與實驗結果差距最大。而基于YLD2000-2D屈服準則及變彈性模量本構模型所得的數值模擬結果與實驗結果比較接近。25 mm彎曲行程下，Mises各向同性本構模型的模擬結果和實驗結果相差2.38°，YLD2000-2D屈服準則及變彈性模量本構模型的模擬結果和實驗結果相差0.35°；30 mm彎曲行程下，前者相差4.41°，后者相差1.68°。

(a)彎曲行程25 mm

(b)彎曲行程30 mm圖14 基于不同本構模型的數值模擬與實驗結果Fig.14 Numerical simulation and experimental results based on different constitutive models

如圖15所示，基于YLD2000-2D及變彈性模量本構模型，25 mm壓彎行程下，Ti-6Al-4V鈦合金板材五點彎曲數值模擬回彈預測精度比Mises各向同性本構模型提高了31.18%;30 mm壓彎行程下，回彈預測精度提高了24.55%。綜上所述，基于YLD2000-2D及變彈性模量的本構模型可以顯著提高Ti-6Al-4V鈦合金板材五點彎曲回彈預測精度。

圖15 不同本構模型在25 mm、30 mm彎曲行程下回彈預測的差異Fig.15 Difference of springback prediction of different constitutive models under 25 mm and 30 mm bending stroke

4 結論

(1)Ti-6Al-4V鈦合金的屈服強度及彈性模量在RD、DD、TD三個方向上存在明顯的各向異性。

(2)Ti-6Al-4V鈦合金彈性模量隨塑性應變增加而減小，最終變為一個定值。基于以上規律，建立了Ti-6Al-4V鈦合金變彈性模量數學模型。

(3)基于YLD2000-2D屈服準則及變彈性模量模型，建立了Ti-6Al-4V鈦合金本構模型，并通過Umat二次開發接口，將其嵌入ABAQUS軟件中進行Ti-6Al-4V鈦合金板材五點彎曲回彈數值模擬。

(4)基于YLD2000-2D屈服準則及變彈性模量的本構模型顯著提高了Ti-6Al-4V鈦合金板材五點彎曲回彈預測精度，相比Mises各向同性本構模型最高提高了31.18%。