一種涵道螺旋槳槳葉高效設(shè)計(jì)方法

郭佳豪，周洲，李旭

西北工業(yè)大學(xué) 航空學(xué)院，西安 710072

涵道螺旋槳，即螺旋槳外部包圍涵道的一種動(dòng)力形式，被廣泛應(yīng)用于航空和航海領(lǐng)域，為飛行器、艦船、潛艇等提供動(dòng)力。相比孤立螺旋槳，涵道螺旋槳具有更高的安全性以及氣動(dòng)效率，因此研究高效的涵道螺旋槳設(shè)計(jì)方法具有較高的工程應(yīng)用價(jià)值。

涵道螺旋槳設(shè)計(jì)方法一般基于葉素動(dòng)量理論、升力線及面元法等快速方法，常用于涵道螺旋槳的初始設(shè)計(jì)。國(guó)外方面，Coney采用環(huán)渦與對(duì)稱(chēng)渦模型等效涵道，并基于升力線模型，提出一種涵道螺旋槳設(shè)計(jì)方法。Stubblefield應(yīng)用Kerwin最優(yōu)環(huán)量求解方法螺對(duì)涵道旋槳進(jìn)行了詳細(xì)的設(shè)計(jì)。此外，Epps和Kimball對(duì)螺旋槳升力線設(shè)計(jì)方法進(jìn)行了研究，并提出一種新的螺旋槳尾渦模型，與經(jīng)典尾渦模型的對(duì)比表明其具有較好的精度，并且魯棒性更高。基于以上研究，Epps等開(kāi)發(fā)了OpenProp螺旋槳設(shè)計(jì)軟件，并將涵道螺旋槳設(shè)計(jì)方法集成其中。

國(guó)內(nèi)方面，劉沛清推導(dǎo)了涵道螺旋槳葉素動(dòng)量理論。高永衛(wèi)等提出一種涵道螺旋槳工程設(shè)計(jì)方法，并根據(jù)軸流風(fēng)機(jī)葉素理論進(jìn)行槳葉設(shè)計(jì)。宋長(zhǎng)紅等建立了基于動(dòng)量源方法的涵道尾槳數(shù)值模擬方法，通過(guò)對(duì)比試驗(yàn)結(jié)果驗(yàn)證了方法的可行性。葉坤等通過(guò)動(dòng)量源方法簡(jiǎn)化槳葉，分別采用響應(yīng)面模型和神經(jīng)網(wǎng)絡(luò)模型，對(duì)NASA涵道進(jìn)行優(yōu)化設(shè)計(jì)。姬樂(lè)強(qiáng)等采用動(dòng)量源方法，研究了唇口半徑、涵道擴(kuò)張角、槳尖間隙及槳葉相對(duì)位置等涵道參數(shù)對(duì)整體氣動(dòng)力的影響，并對(duì)涵道外形進(jìn)行了優(yōu)化設(shè)計(jì)。此外，杜思亮等對(duì)一種開(kāi)口壁式涵道螺旋槳進(jìn)行了研究，并提出一種嵌入式涵道螺旋槳，研究表明懸停及小爬升狀態(tài)下相比于同等尺寸的涵道螺旋槳，其拉力及功率載荷更大。

隨著基于Navier-Stokes(N-S)方程的數(shù)值模擬方法的不斷發(fā)展，多重參考系法(Multiple Reference Frame，MRF)、基于滑移網(wǎng)格及嵌套網(wǎng)格的非定常數(shù)值模擬方法等更高精度的CFD(Computational Fluid Dynamics)求解方法被廣泛應(yīng)用于涵道螺旋槳性能計(jì)算中。但由于CFD計(jì)算耗時(shí)久，尤其是非定常計(jì)算。若應(yīng)用CFD計(jì)算進(jìn)行性能求解，進(jìn)行涵道螺旋槳的優(yōu)化設(shè)計(jì)，雖然設(shè)計(jì)精度高，但設(shè)計(jì)效率低。而對(duì)于快速設(shè)計(jì)方法，由于設(shè)計(jì)方法本身存在一定簡(jiǎn)化，且需確定葉素的氣動(dòng)力信息，故設(shè)計(jì)性能同真實(shí)性能存在一定偏差。

因此，為提高設(shè)計(jì)的精度并保留設(shè)計(jì)的快速性，本文提出一種耦合CFD修正的涵道螺旋槳槳葉設(shè)計(jì)方法，首先采用快速設(shè)計(jì)方法進(jìn)行設(shè)計(jì)，再通過(guò)CFD計(jì)算對(duì)設(shè)計(jì)進(jìn)行修正，兩者迭代，從而在進(jìn)行少量CFD計(jì)算后，得到滿(mǎn)足設(shè)計(jì)要求的結(jié)果。

1 涵道螺旋槳快速設(shè)計(jì)方法

1.1 最小能量損失

涵道螺旋槳葉素受力分析如圖1所示。其中:為來(lái)流速度;為轉(zhuǎn)速;為葉素實(shí)際迎角;為干涉角;為幾何入流角;為實(shí)際入流角;為阻升角;為合速度;為軸向誘導(dǎo)速度;為切向誘導(dǎo)速度;′為幾何誘導(dǎo)速度;為升力;為阻力;為切向力;為拉力。

圖1 葉素受力分析Fig.1 Force analysis of blade element

涵道螺旋槳槳葉設(shè)計(jì)基于最小能量損失原則。若徑向位置處槳葉葉素產(chǎn)生增量擾動(dòng)Δ，使螺旋槳拉力和扭矩分別發(fā)生Δ和Δ增量變化，則螺旋槳有用功與吸收能量對(duì)應(yīng)變化的比值為

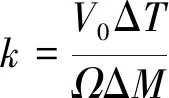
(1)

忽略阻力影響時(shí)，拉力、扭矩變化為

Δ=Δ(-)d

(2)

Δ=Δ(+)d

(3)

式中:為空氣密度。

根據(jù)圖1幾何關(guān)系式可得

(4)

聯(lián)立式(1)～式(4)，可得

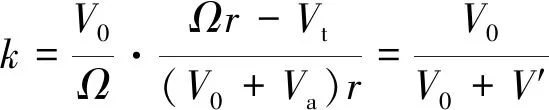
(5)

要使螺旋槳效率最高，則需在值大處增加環(huán)量，值小處減小環(huán)量。故最小能量損失要求沿槳葉分布為常數(shù)。又由式(5)可知，此時(shí)′沿槳葉的分布亦為定值。因此涵道螺旋槳槳葉的設(shè)計(jì)便是求解滿(mǎn)足設(shè)計(jì)要求的′，進(jìn)而確定各葉素的狀態(tài)。

1.2 涵道螺旋槳葉素動(dòng)量理論

對(duì)于涵道螺旋槳，槳葉提供一部分拉力外，涵道壁面也提供一部分拉力。假設(shè)槳葉拉力占比為，表示螺旋槳槳葉拉力，則

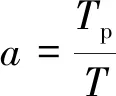
(6)

設(shè)涵道螺旋槳噴流的軸向誘導(dǎo)速度為，槳葉處的誘導(dǎo)速度為、，由動(dòng)量定理及動(dòng)量矩定理可知

d=2π(+)d

(7)

d=4π(+)d

(8)

d=2π(+)d

(9)

而根據(jù)動(dòng)量理論可知槳葉的拉力：

=2π(+2)d

(10)

式中:為槳盤(pán)面積;Δ為槳盤(pán)前后壓差。由式(9)、式(10)求得軸向誘導(dǎo)速度間的關(guān)系：

=2[+(-1)]

(11)

對(duì)于涵道螺旋槳，根據(jù)圖1所示葉素幾何關(guān)系并結(jié)合式(8)、式(9)可知：

(12)

故槳葉處軸向誘導(dǎo)速度和切向誘導(dǎo)速度的關(guān)系為

=[+(-1)]tan(+)

(13)

(14)

式中:和分別為升力系數(shù)和阻力系數(shù)。

又由式(4)可知：

′=tan+

(15)

聯(lián)立式(13)及式(15)，推導(dǎo)可得槳葉誘導(dǎo)速度同′的關(guān)系：

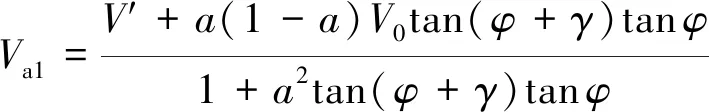
(16)

(17)

1.3 快速設(shè)計(jì)方法

給定設(shè)計(jì)高度、來(lái)流速度及設(shè)計(jì)拉力，并確定涵道外形，在此基礎(chǔ)上進(jìn)行涵道螺旋槳槳葉設(shè)計(jì)。

槳葉拉力占比與涵道外形相關(guān)，涵道外形確定則設(shè)計(jì)狀態(tài)下的確定，同時(shí)螺旋槳半徑確定。再選定槳葉翼型，確定設(shè)計(jì)狀態(tài)下的葉素迎角、升力系數(shù)及阻力系數(shù)，通過(guò)設(shè)計(jì)得到各葉素的弦長(zhǎng)及扭轉(zhuǎn)角，從而得到涵道螺旋槳的槳葉外形。設(shè)計(jì)過(guò)程為

1) 確定槳葉數(shù)及轉(zhuǎn)速，并將槳葉劃分為個(gè)截面。

2) 根據(jù)設(shè)計(jì)拉力及設(shè)計(jì)狀態(tài)求解′，確定處葉素的弦長(zhǎng)及扭轉(zhuǎn)角。

給定初始′，得到入流角：

(18)

根據(jù)式(16)、式(17)，可確定誘導(dǎo)速度，進(jìn)而得到合速度及環(huán)量：

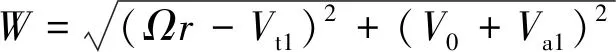
(19)

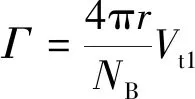
(20)

葉素升力與當(dāng)?shù)丨h(huán)量關(guān)系為

d=d

(21)

而升力又可表示為

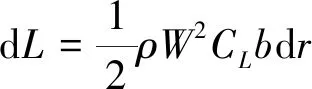
(22)

聯(lián)立式(21)～式(22)可得

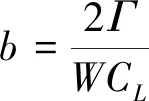
(23)

故確定合速度及環(huán)量后，通過(guò)式(23)可求得葉素弦長(zhǎng)。

對(duì)于寬度為d的葉素，其產(chǎn)生的拉力d、扭矩d及總拉力d為

(24)

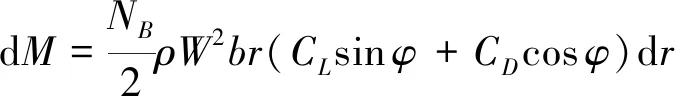
(25)

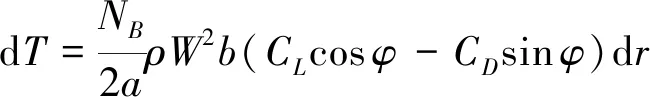
(26)

則總拉力為

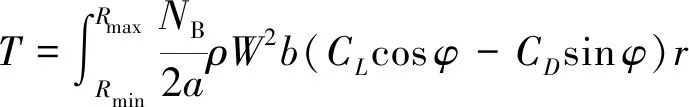
(27)

式中:和分別為槳葉的最大和最小半徑。

采用Newton迭代求解上式，可得到滿(mǎn)足設(shè)計(jì)拉力要求的′，從而確定各個(gè)截面的受力幾何關(guān)系。最終得到該截面的設(shè)計(jì)弦長(zhǎng)，及對(duì)應(yīng)的扭轉(zhuǎn)角：

=+

(28)

3) 重復(fù)求解，得到所有設(shè)計(jì)截面的弦長(zhǎng)及扭轉(zhuǎn)角。

2 涵道螺旋槳數(shù)值模擬方法

采用求解雷諾平均N-S方程的“多重參考系法”對(duì)涵道螺旋槳的性能進(jìn)行計(jì)算，湍流模型采用SA湍流模型，并采用結(jié)構(gòu)網(wǎng)格進(jìn)行網(wǎng)格生成。

為驗(yàn)證數(shù)值模擬方法的可行性，對(duì)文獻(xiàn)[20] 中的NASA涵道螺旋槳模型進(jìn)行計(jì)算，幾何模型如圖2所示。該模型有3片槳葉，槳盤(pán)直徑0.381 0 m，槳轂直徑0.109 2 m，槳轂長(zhǎng)0.392 7 m，涵道外壁最大直徑0.464 3 m，涵道長(zhǎng)0.261 9 m，具體尺寸詳見(jiàn)文獻(xiàn)[20]。

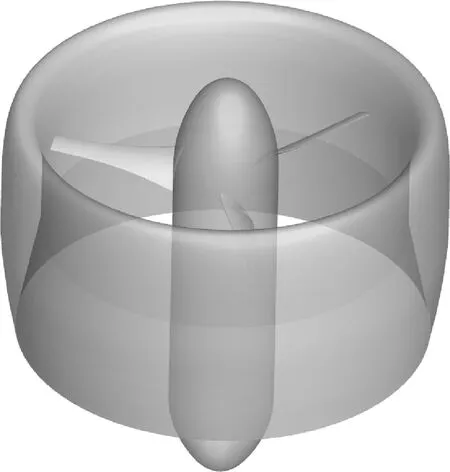
圖2 NASA涵道螺旋槳幾何模型Fig.2 Geometry model of NASA ducted propeller

對(duì)其進(jìn)行網(wǎng)格劃分，將計(jì)算區(qū)域分為 “旋轉(zhuǎn)域”與其外的“外流域”，如圖3所示，“旋轉(zhuǎn)域”包含部分內(nèi)壁、部分槳轂及槳葉，槳間間隙完全包含在旋轉(zhuǎn)域內(nèi)，兩域流場(chǎng)交界面處采用通量的計(jì)算傳遞信息。生成341萬(wàn)及458萬(wàn)總網(wǎng)格數(shù)量的兩套網(wǎng)格，以驗(yàn)證網(wǎng)格無(wú)關(guān)性。341萬(wàn)總網(wǎng)格數(shù)量對(duì)應(yīng)的局部網(wǎng)格如圖4所示，槳葉第1層網(wǎng)格對(duì)應(yīng)的取1。

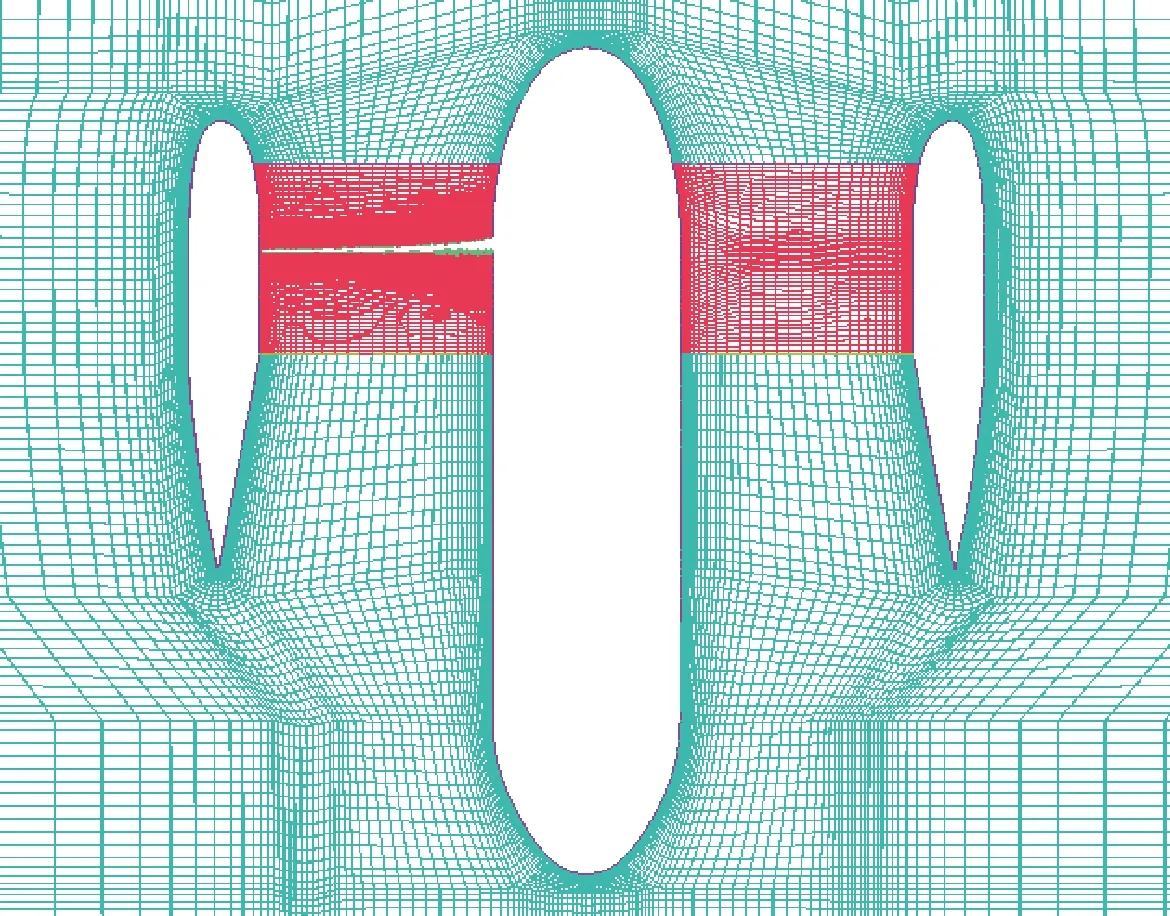
圖3 不同流域網(wǎng)格示意圖Fig.3 Grid sketch of different flow fields

采用上述方法對(duì)NASA涵道螺旋槳進(jìn)行計(jì)算，計(jì)算為懸停狀態(tài)，轉(zhuǎn)速8 000 r/min，結(jié)果如表1 所示。

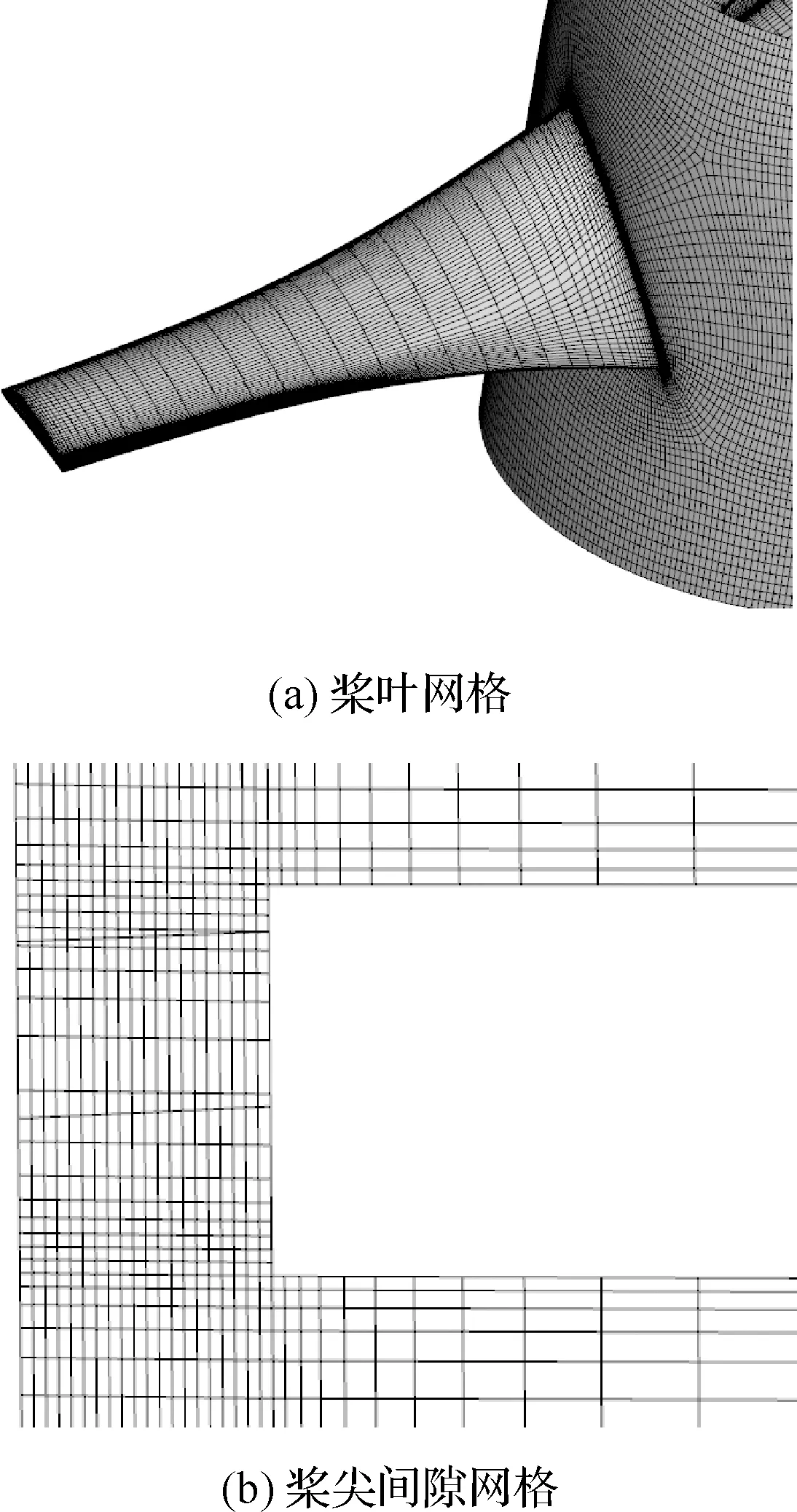
圖4 局部網(wǎng)格示意圖Fig.4 Schematic diagram of local mesh

兩種網(wǎng)格的計(jì)算結(jié)果相差不大，“341萬(wàn)網(wǎng)格總量”的計(jì)算結(jié)果相比實(shí)驗(yàn)值偏小，槳葉拉力誤差9.21%，扭矩誤差7.05%，涵道拉力誤差9.88%，所有誤差均在10%以?xún)?nèi)，基本驗(yàn)證了所用數(shù)值模擬方法求解的可行性。下文進(jìn)行相關(guān)數(shù)值模擬時(shí)保持網(wǎng)格拓?fù)浣Y(jié)構(gòu)相同，網(wǎng)格總量不少于341萬(wàn)。

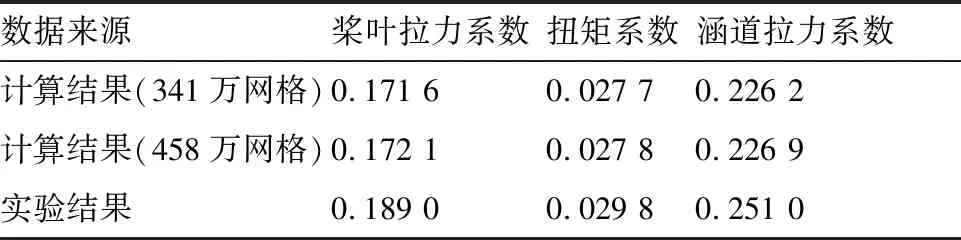
表1 氣動(dòng)力計(jì)算和實(shí)驗(yàn)結(jié)果對(duì)比

3 設(shè)計(jì)目標(biāo)及結(jié)果

3.1 設(shè)計(jì)目標(biāo)

采用快速設(shè)計(jì)方法進(jìn)行涵道螺旋槳槳葉設(shè)計(jì)。設(shè)計(jì)高度=0 km，來(lái)流速度=0 m/s，總拉力=300 N。涵道外形采用上述“NASA涵道”，取槳葉拉力占比=0.430。槳盤(pán)半徑=0.190 5 m，槳轂半徑=0.054 61 m，槳尖間隙001。螺旋槳轉(zhuǎn)速=8 000 r/min，槳葉數(shù)=8。

槳葉翼型采用圖5所示翼型族，翼型彎度保持不變，厚度由槳根至槳尖線性減小。由于翼型的彎度一致，且厚度變化較小，故認(rèn)為各翼型相同迎角下的氣動(dòng)力一致。給定設(shè)計(jì)迎角=2°，升力系數(shù)=0600，阻力系數(shù)=0023。

圖5 翼型示意圖Fig.5 Schematic diagram of airfoil

3.2 設(shè)計(jì)結(jié)果

槳葉弦長(zhǎng)及扭轉(zhuǎn)角設(shè)計(jì)結(jié)果如圖6所示。采用第2節(jié)數(shù)值模擬方法進(jìn)行涵道螺旋槳性能計(jì)算。

設(shè)計(jì)結(jié)果與計(jì)算結(jié)果如表2所示。可以看出，基于MRF的CFD計(jì)算得到的拉力、扭矩及功率載荷均小于設(shè)計(jì)結(jié)果，這說(shuō)明上述快速設(shè)計(jì)方法存在一定缺陷。可能的原因有兩方面：一方面，設(shè)計(jì)時(shí)給定的葉素氣動(dòng)力不能保證與實(shí)際相同，兩者存在一定誤差；另一方面，葉素的誘導(dǎo)速度不準(zhǔn)確，設(shè)計(jì)時(shí)采用的入流角偏小，使得槳葉的扭轉(zhuǎn)角偏小。

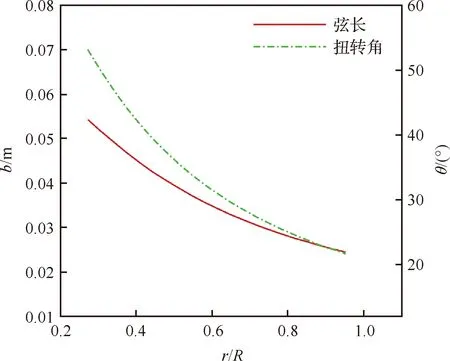
圖6 弦長(zhǎng)與扭轉(zhuǎn)角設(shè)計(jì)結(jié)果Fig.6 Design results of chord length and twist angle

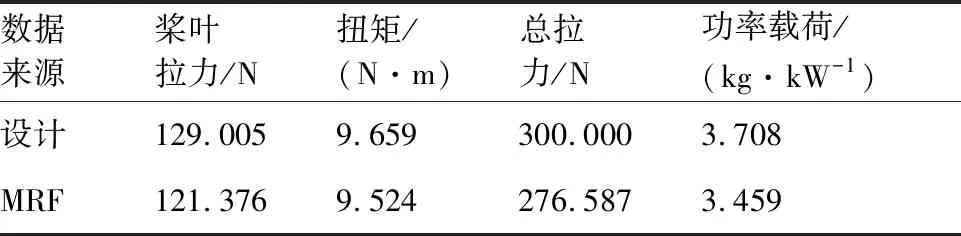
表2 涵道螺旋槳性能對(duì)比Table 2 Comparison of performance of ducted propeller

4 耦合CFD求解的高效設(shè)計(jì)方法

4.1 入流角修正

基于3.2節(jié)的分析，對(duì)文中的快速設(shè)計(jì)方法進(jìn)行完善。

對(duì)于給定的′，首先按1.3節(jié)中式(18)～式(23) 計(jì)算得到弦長(zhǎng)。但在計(jì)算槳葉氣動(dòng)力前，通過(guò)修正系數(shù)，對(duì)′進(jìn)行修正：

(29)

再使用新的′根據(jù)式(16)～式(19)計(jì)算修正后的誘導(dǎo)速度、入流角及合速度，最后計(jì)算修正后的葉素氣動(dòng)力。

對(duì)′進(jìn)行修正是為了保證最小能量損失原則在修正后同樣滿(mǎn)足，以避免修正導(dǎo)致效率降低。

采用修正的快速設(shè)計(jì)方法對(duì)涵道螺旋槳槳葉進(jìn)行設(shè)計(jì)，不同修正系數(shù)對(duì)應(yīng)的CFD計(jì)算結(jié)果如表3所示。可以看出，當(dāng)=105時(shí)，CFD計(jì)算結(jié)果與設(shè)計(jì)值接近，說(shuō)明通過(guò)合理的修正，能夠提高設(shè)計(jì)的精度。

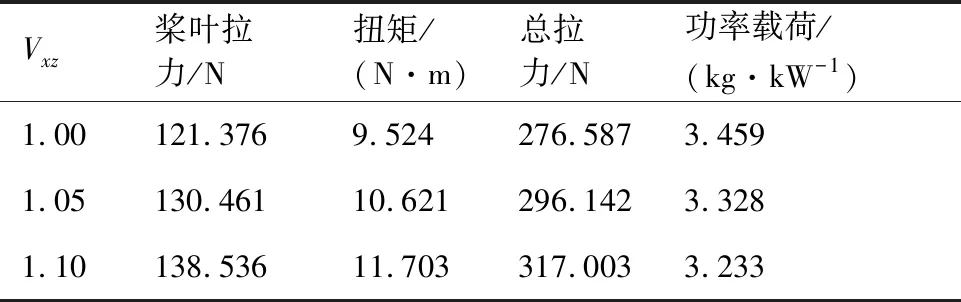
表3 不同修正系數(shù)下的涵道螺旋槳性能對(duì)比

4.2 氣動(dòng)力修正

葉素真實(shí)狀態(tài)下的迎角及升阻力系數(shù)與設(shè)計(jì)給定的值存在一定偏差，若忽略阻力的影響，可認(rèn)為氣動(dòng)力的偏差為迎角與升力系數(shù)的不匹配。因此，這里不改變升阻力系數(shù)，通過(guò)修正迎角進(jìn)行氣動(dòng)力的修正。

4.3 拉力占比修正

實(shí)際設(shè)計(jì)時(shí)，涵道外形根據(jù)設(shè)計(jì)而定，也是一個(gè)未知的變量，設(shè)計(jì)前往往不能確定設(shè)計(jì)狀態(tài)下拉力占比的準(zhǔn)確值。因此，設(shè)計(jì)前可首先給出的初值，在設(shè)計(jì)迭代中，根據(jù)CFD計(jì)算結(jié)果更新，從而使設(shè)計(jì)結(jié)果更準(zhǔn)確，也使設(shè)計(jì)方法適用于不同涵道外形的涵道螺旋槳。

4.4 修正參數(shù)求解

引入′修正對(duì)設(shè)計(jì)方法進(jìn)行改善，取得了較好的效果，但其前提是得到合理的。而不同設(shè)計(jì)狀態(tài)下可能不同，若通過(guò)試錯(cuò)來(lái)選取，可能需大量的CFD計(jì)算驗(yàn)證，使得設(shè)計(jì)效率降低。實(shí)際上，CFD計(jì)算結(jié)果可作為一種重要的參考，為的選取提供參考。因此這里提出一種通過(guò)CFD計(jì)算結(jié)果反解修正參數(shù)的方法。

該方法的思想是：通過(guò)構(gòu)造滿(mǎn)足CFD結(jié)果的葉素狀態(tài)，求解真實(shí)狀態(tài)下的入流角，確定修正系數(shù)；并對(duì)給定的葉素氣動(dòng)力進(jìn)行修正，修正設(shè)計(jì)給定的迎角；最后更新槳葉的拉力占比。具體步驟如下：

給定初始，以CFD求解得到槳葉的拉力為設(shè)計(jì)目標(biāo)，采用修正的快速設(shè)計(jì)方法進(jìn)行槳葉設(shè)計(jì)，得到設(shè)計(jì)的拉力及扭矩。

由于葉素阻力較小，且入流角一般較大，因此忽略阻力影響時(shí)，由式(24)、式(25)可知：

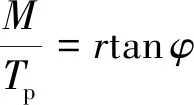
(30)

槳葉拉力及扭矩實(shí)際反映了真實(shí)的入流角。故通過(guò)迭代求解，最終得到與CFD所得相同的設(shè)計(jì)結(jié)果，此時(shí)的即為入流角修正系數(shù)。

獲得的同時(shí)得到修正后的入流角，已知涵道螺旋槳的扭轉(zhuǎn)角，進(jìn)而根據(jù)式(28) 求得各葉素的迎角，求其均值得到修正迎角：

(31)

最后根據(jù)CFD計(jì)算得到的總拉力及槳葉拉力，由式(6)求得真實(shí)的拉力占比。

4.5 耦合CFD求解的涵道螺旋槳槳葉設(shè)計(jì)

基于以上方法及分析，提出耦合CFD修正的涵道螺旋槳槳葉高效設(shè)計(jì)方法，步驟如下：

根據(jù)1.3節(jié)快速設(shè)計(jì)方法，設(shè)計(jì)得到初始槳葉(弦長(zhǎng)及扭轉(zhuǎn)角分布)。

通過(guò)CFD計(jì)算獲得槳葉拉力及扭矩。

根據(jù)CFD計(jì)算結(jié)果求解修正系數(shù)及修正迎角，并更新槳葉拉力占比。

根據(jù)求得的修正參數(shù)采用修正的快速設(shè)計(jì)方法進(jìn)行再設(shè)計(jì)。

重復(fù)步驟2～步驟4，得到滿(mǎn)足設(shè)計(jì)要求的結(jié)果。

設(shè)計(jì)流程如圖7所示。

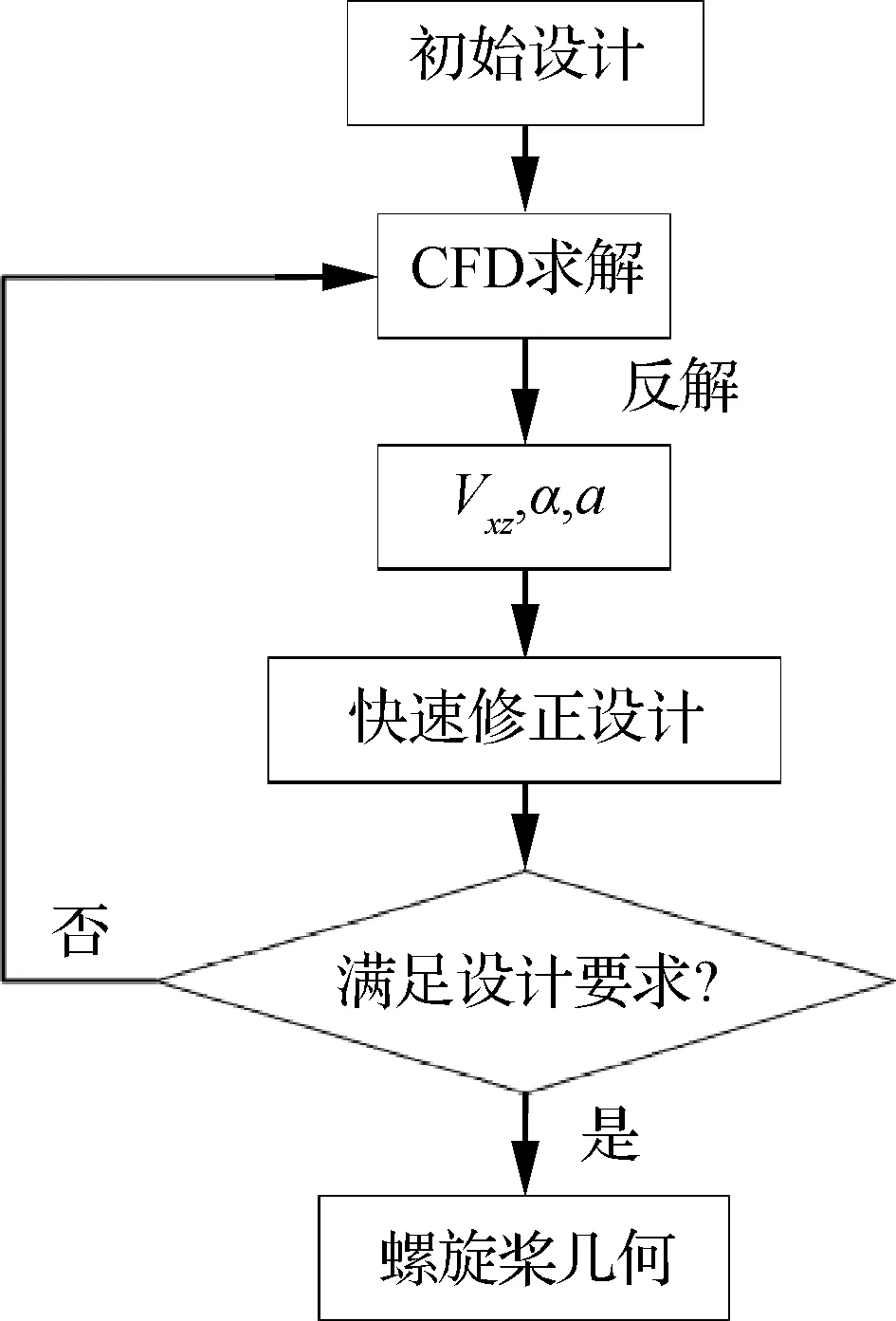
圖7 耦合CFD求解的涵道螺旋槳槳葉設(shè)計(jì)流程Fig.7 Design process of ducted propeller blade coupled with CFD correction

5 結(jié)果與分析

5.1 修正結(jié)果對(duì)比

采用修正設(shè)計(jì)方法對(duì)表2的初始結(jié)果進(jìn)行修正，以此再設(shè)計(jì)，結(jié)果如表4所示。修正2次后的CFD結(jié)果已經(jīng)十分接近設(shè)計(jì)結(jié)果，對(duì)應(yīng)=1094，=1215°，=0438。設(shè)計(jì)得到的涵道螺旋槳幾何如圖8所示。

為證明方法的可行性，對(duì)表3中=110的初始設(shè)計(jì)進(jìn)行修正及再設(shè)計(jì)，結(jié)果如表5所示。同樣，修正2次后，CFD結(jié)果基本與設(shè)計(jì)結(jié)果相同，滿(mǎn)足設(shè)計(jì)要求。一方面，說(shuō)明文中的設(shè)計(jì)方法具備快速收斂的特點(diǎn)；另一方面，設(shè)計(jì)結(jié)果與CFD計(jì)算結(jié)果間的差距隨著設(shè)計(jì)迭代次數(shù)的增加而逐漸減小，最終趨于一致。

表4 修正前后涵道螺旋槳性能

圖8 涵道螺旋槳幾何Fig.8 Geometry of ducted propeller

經(jīng)2次修正設(shè)計(jì)后，各修正系數(shù)分別為：=1095，=1187°，=0435，與上述修正參數(shù)結(jié)果基本相同。進(jìn)一步對(duì)比弦長(zhǎng)及扭轉(zhuǎn)角設(shè)計(jì)結(jié)果，如圖9所示，兩者幾何也基本一致，說(shuō)明不同初始位置最終收斂至同一結(jié)果。表明文中采用的設(shè)計(jì)方法是收斂的，同時(shí)具備較好的魯棒性。

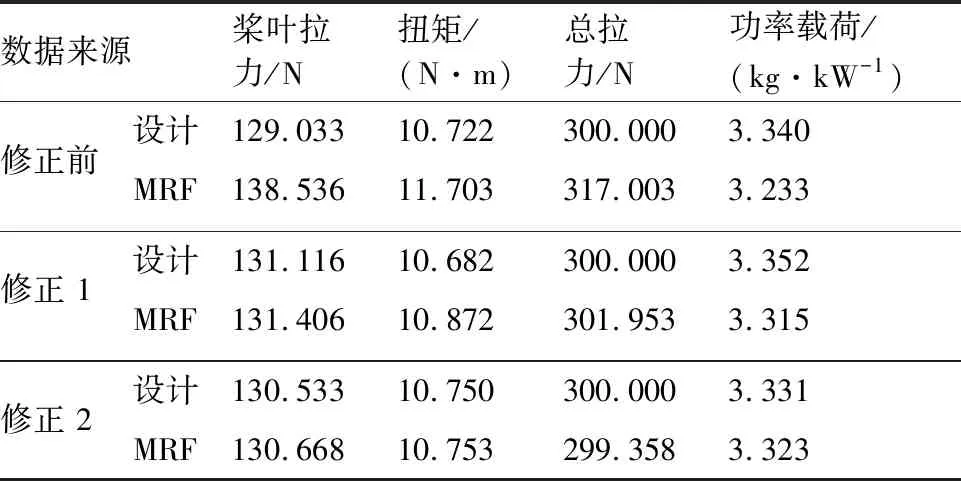
表5 修正前后涵道螺旋槳性能(Vxz=1.1)

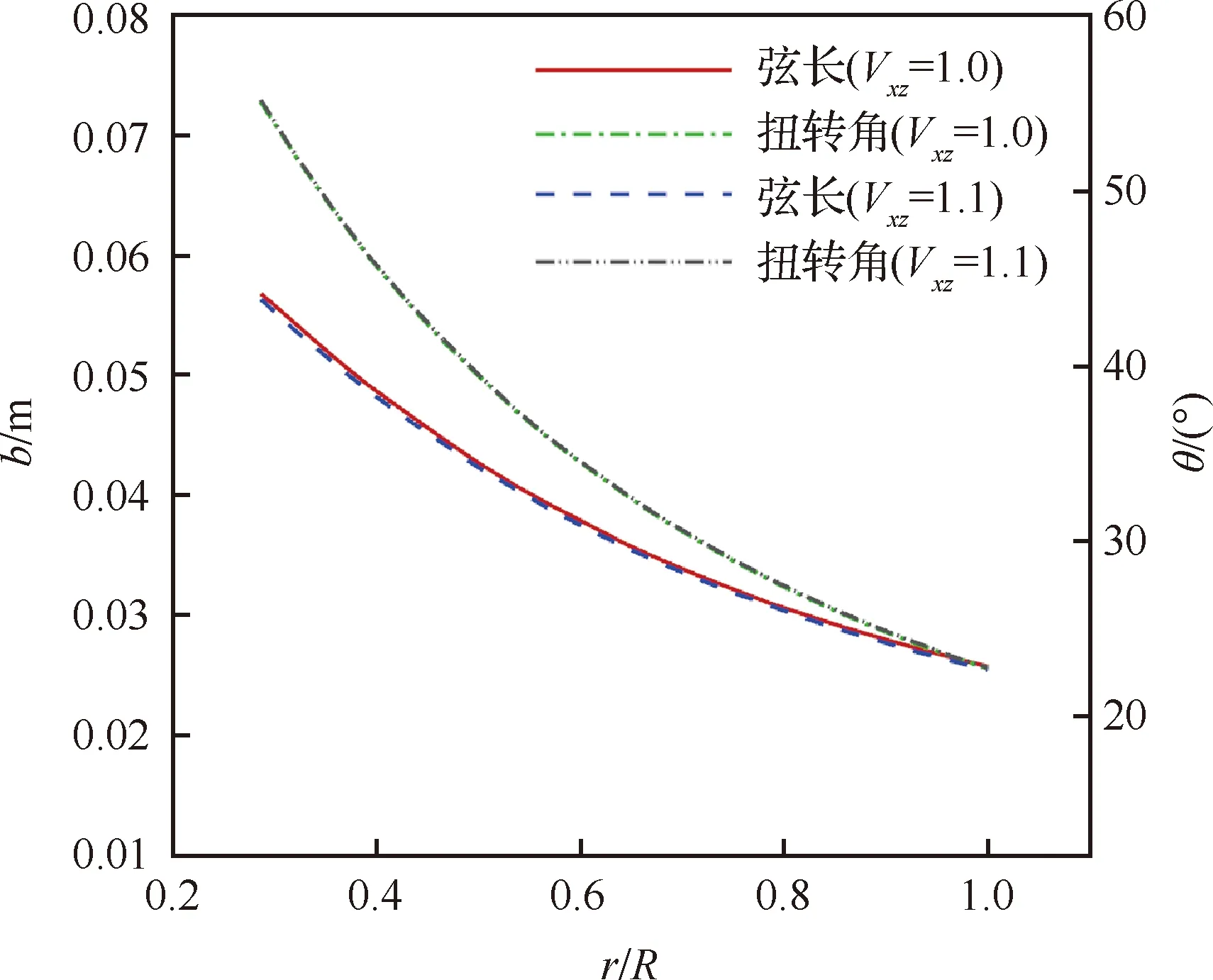
圖9 不同初始修正系數(shù)設(shè)計(jì)得到的弦長(zhǎng)與扭轉(zhuǎn)角設(shè)計(jì)對(duì)比Fig.9 Comparison of chord length and twist angle obtained by design of different initial correction factors

5.2 不同涵道外形設(shè)計(jì)驗(yàn)證

為進(jìn)一步驗(yàn)證設(shè)計(jì)方法，設(shè)計(jì)一種小型涵道螺旋槳。并采用圖10所示的無(wú)擴(kuò)張及收縮出口的簡(jiǎn)易涵道外形，以檢驗(yàn)設(shè)計(jì)方法在不同涵道外形下的可行性。

圖10 簡(jiǎn)易涵道外形示意圖Fig.10 Schematic diagram of a simple shape of duct

取設(shè)計(jì)高度=0 km，來(lái)流速度=0 m/s，總拉力=15 N，槳盤(pán)半徑=0.050 m，槳轂半徑=0.020 m，槳尖間隙001。取螺旋槳轉(zhuǎn)速=20 000 r/min，槳葉數(shù)N=8，初始槳葉拉力占比初值=0500。同樣采用圖2所示翼型族，給定葉素設(shè)計(jì)迎角=2°，升力系數(shù)=0600，阻力系數(shù)=0023。

初始設(shè)計(jì)取=1000，小型涵道螺旋槳的設(shè)計(jì)結(jié)果如圖11及圖12所示，修正前后的性能見(jiàn)表6。可以看出，設(shè)計(jì)結(jié)果與計(jì)算結(jié)果趨于收斂，經(jīng)過(guò)2次修正設(shè)計(jì)，基本滿(mǎn)足設(shè)計(jì)要求，對(duì)應(yīng)=1060，=0574°，=0581。

圖11 小型涵道螺旋槳弦長(zhǎng)與扭轉(zhuǎn)角設(shè)計(jì)結(jié)果Fig.11 Design results of chord length and twist angle of small ducted propeller

圖12 小型涵道螺旋槳幾何Fig.12 Geometry of small ducted propeller

涵道外形對(duì)設(shè)計(jì)的影響體現(xiàn)在槳葉拉力占比之上。對(duì)于該簡(jiǎn)易涵道，可認(rèn)為噴流無(wú)擴(kuò)張和收縮，而槳轂的存在使得噴流存在一定的收縮，因此設(shè)計(jì)結(jié)果>0500，符合動(dòng)量理論的結(jié)論。同時(shí)也驗(yàn)證了本文所采用的設(shè)計(jì)方法適用于不同涵道形式。

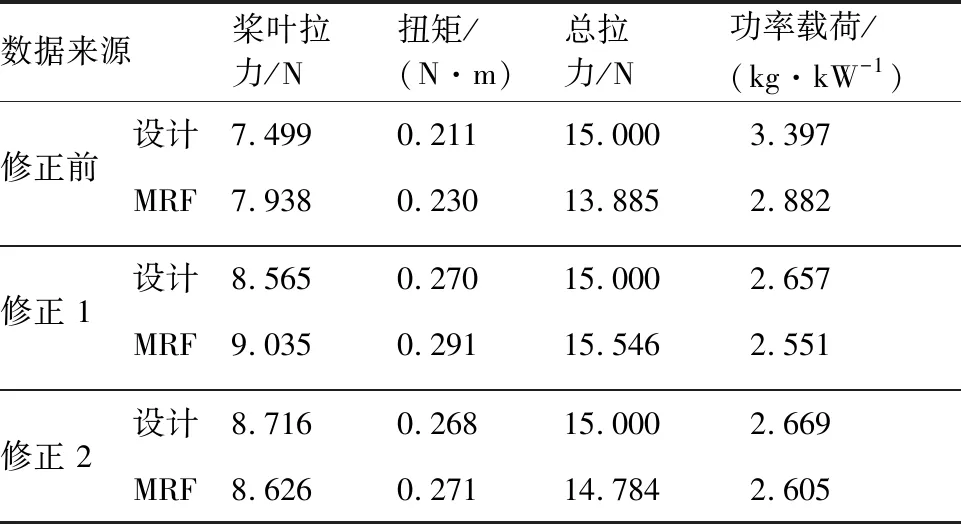
表6 修正前后小型涵道螺旋槳性能

5.3 有來(lái)流狀態(tài)設(shè)計(jì)驗(yàn)證

以上設(shè)計(jì)均在無(wú)來(lái)流狀態(tài)下進(jìn)行設(shè)計(jì)，為驗(yàn)證設(shè)計(jì)方法在有來(lái)流狀態(tài)下的可行性，在3.1節(jié)設(shè)計(jì)狀態(tài)的基礎(chǔ)上，改變來(lái)流速度為=20 m/s，同時(shí)改變槳葉拉力占比初值=06，以此進(jìn)行設(shè)計(jì)。

有來(lái)流狀態(tài)涵道螺旋槳的設(shè)計(jì)結(jié)果如圖13及圖14所示，設(shè)計(jì)前后的性能見(jiàn)表7, 最終修正參數(shù)=1078，=1056°，=0577。可以看出，經(jīng)過(guò)2次修正設(shè)計(jì)后，設(shè)計(jì)與計(jì)算間的拉力誤差基本控制在2%以?xún)?nèi)，驗(yàn)證了文中涵道螺旋槳槳葉設(shè)計(jì)方法在有來(lái)流狀態(tài)下設(shè)計(jì)的可行性。

以上設(shè)計(jì)驗(yàn)證均表明，文中的設(shè)計(jì)結(jié)果收斂于CFD計(jì)算結(jié)果。因此，只需保證CFD計(jì)算的準(zhǔn)確性，則能保證文中設(shè)計(jì)方法設(shè)計(jì)的準(zhǔn)確性。

圖13 有來(lái)流狀態(tài)涵道螺旋槳弦長(zhǎng)與扭轉(zhuǎn)角設(shè)計(jì)結(jié)果Fig.13 Design result of chord length and twist angle of ducted propeller in incoming flow state

圖14 有來(lái)流狀態(tài)涵道螺旋槳幾何Fig.14 Geometry of ducted propeller in incoming flow state

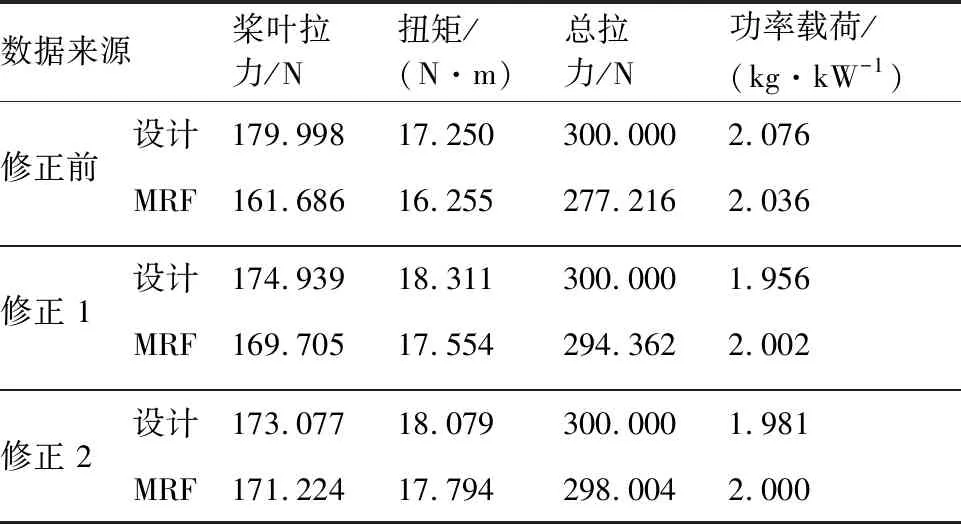
表7 有來(lái)流狀態(tài)修正前后涵道螺旋槳性能

6 結(jié) 論

本文建立了基于葉素動(dòng)量理論的涵道螺旋槳快速設(shè)計(jì)方法，并通過(guò)耦合CFD計(jì)算對(duì)葉素入流角及迎角進(jìn)行修正，提出了一種涵道螺旋槳槳葉高效設(shè)計(jì)方法，并通過(guò)對(duì)不同狀態(tài)的涵道螺旋槳進(jìn)行設(shè)計(jì)及計(jì)算，驗(yàn)證了方法的可行性。得到的結(jié)論如下：

1) 基于葉素動(dòng)量理論的快速設(shè)計(jì)方法，設(shè)計(jì)前不能準(zhǔn)確地給出葉素氣動(dòng)力及槳葉拉力占比，導(dǎo)致設(shè)計(jì)的入流角與實(shí)際結(jié)果存在一定差距，因此造成設(shè)計(jì)結(jié)果與CFD計(jì)算結(jié)果間的偏差。

2) 涵道外形對(duì)設(shè)計(jì)的影響體現(xiàn)在槳葉拉力占比之上，而槳葉拉力、扭矩的比例反映了葉素入流角信息。通過(guò)對(duì)CFD計(jì)算結(jié)果進(jìn)行反解，可得到真實(shí)的葉素入流角，進(jìn)而求得真實(shí)的葉素迎角，同時(shí)求得真實(shí)的槳葉拉力占比。

3) 通過(guò)求解入流角修正系數(shù)、修正迎角及真實(shí)槳葉拉力占比，并以此進(jìn)行涵道螺旋槳槳葉的再設(shè)計(jì)，可得到趨于設(shè)計(jì)要求的結(jié)果。不同初始結(jié)果、不同涵道外形及不同設(shè)計(jì)狀態(tài)的設(shè)計(jì)驗(yàn)證表明，文中設(shè)計(jì)方法基本進(jìn)行2次CFD計(jì)算修正與再設(shè)計(jì)便能滿(mǎn)足設(shè)計(jì)要求，設(shè)計(jì)高效。

4) 本文設(shè)計(jì)方法的設(shè)計(jì)結(jié)果與CFD計(jì)算結(jié)果間的差距隨著設(shè)計(jì)迭代次數(shù)的增加而逐漸減小，設(shè)計(jì)結(jié)果最終收斂于CFD計(jì)算結(jié)果。因此，確保CFD計(jì)算的準(zhǔn)確性，則能夠確保設(shè)計(jì)方法的準(zhǔn)確性。