HSM標準模型的風噪聲源及其特性分析*

胡興軍，毛靖銘，張揚輝，劉一塵，馬家義，喬俊賢，余天明

（1. 吉林大學，汽車仿真與控制國家重點實驗室，長春 130022；2. 一汽奔騰轎車有限公司，長春 130022）

前言

隨著我國汽車技術的發展，消費者對汽車品質的追求日益增加。噪聲是客戶對汽車品質最直觀的感受。高速行駛時，氣動噪聲對駕乘舒適性的影響越來越重要。隨著電動汽車的興起，由風噪引起的內部噪聲受到越來越多的關注。如何對內部噪聲進行有效仿真以探究內部噪聲特性也一直是研究熱點。

仿真計算是研究汽車風噪的重要手段，但是以往多數仿真計算只針對外部噪聲，評價指標為外部監測點，對內部噪聲特性研究較少。近年來，不少國內外學者開始研究內部噪聲計算。2017 年，Schell等提出了有限元、邊界元和SEA 的廣義邊界方法相結合的方法，可用于計算寬頻的車內噪聲。2020年，Hu 等采用不可壓縮CFD 求解器和振動聲學模型計算商用車外流場特性和內部聲場響應。2021年，Wang 等用不可壓縮的LES 與有限元法結合計算乘用車的內部噪聲，研究了車底流動噪聲對車內噪聲的貢獻。計算車內噪聲時，聲源來源越廣，計算資源和時長要求越高，由于外部聲源構成復雜，聲源選取困難，因此研究車內噪聲時，如何合理有效地選擇仿真聲源十分重要。

本文中以HSM（Hyundai simple model）標準模型為研究對象，通過實驗與仿真研究以駕駛員耳側噪聲水平為目標時，合理聲源的選擇及聲源成分與其對內部噪聲的貢獻。分為實驗、流場和聲場仿真3個部分。在實驗部分中對HSM 標準模型的實驗數據進行分析，研究不同噪聲源對內部噪聲的貢獻及其受風速影響的變化規律；在流場和聲場仿真部分中基于實驗結果分別驗證流場和聲場仿真結果，并對流場結構和噪聲源成分及其貢獻度進行分析，由隔聲理論對成分差異的機理做出闡釋。由此獲得通用性結論，為實際車型風噪控制提供仿真策略和指導。

1 實驗部分

1.1 HSM標準模型

HSM 標準模型是一種可用于車內噪聲實驗和數值研究的模型。本次實驗所用HSM標準模型構成及連接方式如圖1 所示，其外廓尺寸長為2 m，寬和高各1 m（××= 2 m × 1 m × 1 m），模型除車窗外，其余部件均為鋁結構，車窗玻璃統一為4 mm 普通鋼化玻璃。模型整體使用密封膠進行密封，防止泄露噪聲的出現。

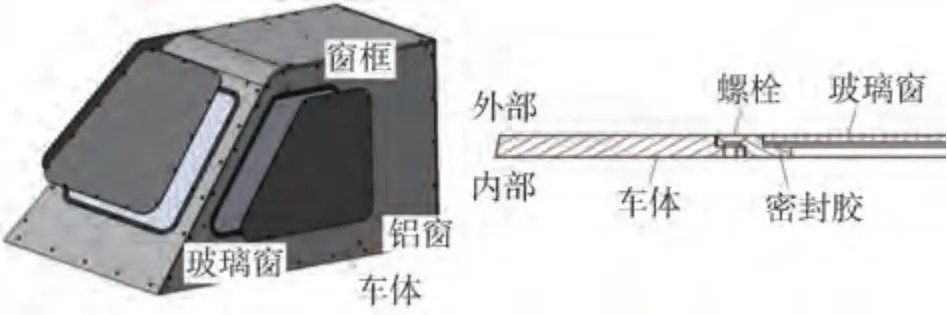
圖1 HSM標準模型

為保證車窗是內部噪聲的唯一聲源，對模型內部進行噪聲控制處理（NCT）。針對鋁表面的傳聲區域，在模型內部進行如圖2 所示的噪聲處理，記為NCT_1，而玻璃表面的傳聲區域，內部不做任何處理，記為NCT_2。

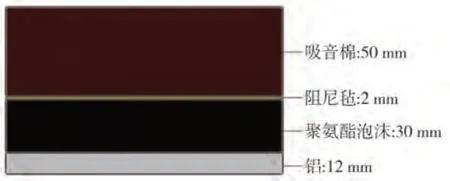
圖2 HSM標準模型內部聲學處理布置圖

1.2 實驗設置

本次噪聲實驗在吉林大學汽車風洞實驗室進行，混響實驗在一汽轎車半消聲室進行。

1.2.1 表面壓力測量實驗

考慮到HSM 標準模型本身的對稱性，僅在模型左側窗進行表面壓力測量。實驗風速為120 km/h，測量點在側窗橫縱方向上均勻布置，實驗測點及裝置布置如圖3所示。

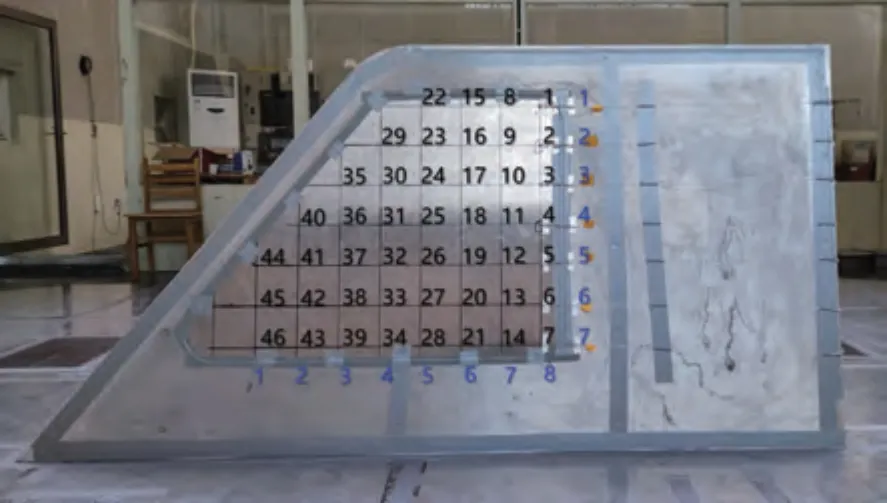
圖3 表面壓力測點及裝置布置圖

1.2.2 內部噪聲測量實驗

內部噪聲實驗的測點參照文獻［6］中布置在駕駛員左耳側，實驗共設置5 種測量工況，分別為全鋁窗、全玻璃窗、單左側玻璃窗、單右側玻璃窗和單前玻璃窗，如圖4 所示。其中單側玻璃窗工況表示實驗布置時僅有該側為玻璃窗，其余車窗為經如圖2所示的噪聲控制處理的鋁窗。測量各工況在不同風速下內部測點的噪聲水平。

圖4 內部噪聲測量布置圖

1.2.3 混響時間測量實驗

為提供后續聲場仿真所需對腔內材料吸收與反射作用的模擬參數，進行混響時間測量實驗。本實驗一共設計3 個方案，各方案下體積聲源分別置于HSM 標準模型地板的前中后3 個位置進行發聲，對于每種聲源位置，均采用模型前后的兩個傳聲器進行測量，不同方案中傳聲器位置保持不變，每種方案下重復測量3次，實驗布置如圖5所示。

圖5 混響時間測量布置圖

1.3 實驗數據分析

1.3.1 表面壓力測量實驗分析

圖6為表面壓力測量結果。由圖可知，側窗表面壓力波動呈現明顯的規律性?？v向上表面壓力數值呈先減小后增大的趨勢，存在明顯拐點。由此可見，側窗上存在一條壓力分界線。

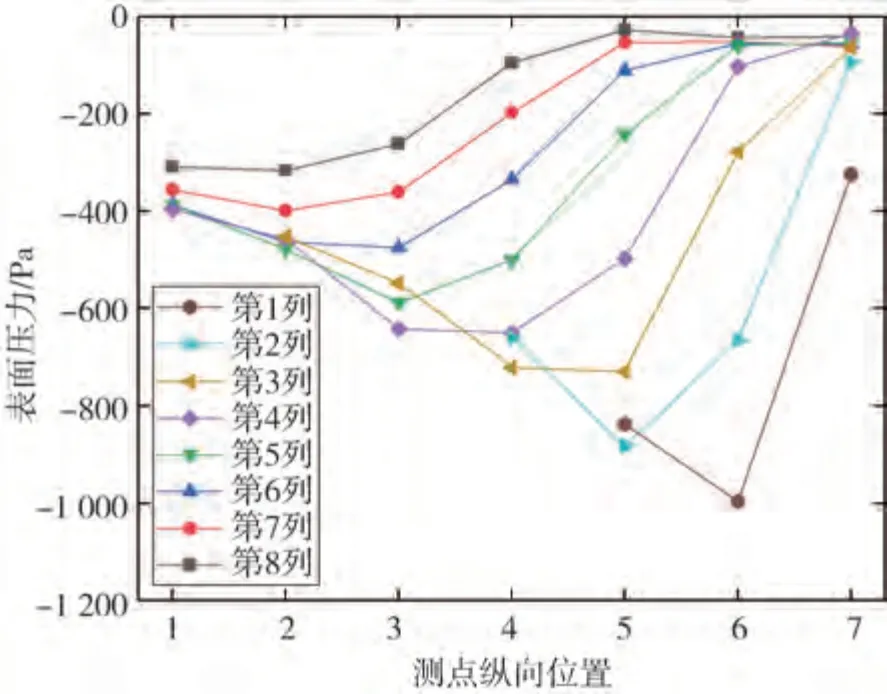
圖6 左側窗表面壓力曲線

結合各拐點位置，擬合得到如圖7 所示的壓力分界線。側窗壓力分界線與水平方向的夾角約呈30°，由此推測實際側窗壓力分界線與水平方向約成29°～30°的夾角。

圖7 側窗壓力分界線

1.3.2 內部噪聲測量實驗分析

（1）風速對內部噪聲的影響

圖8為不同工況下不同風速測點噪聲的頻譜圖。由圖可知，隨風速增加，各工況的頻譜曲線變化規律隨風速變化基本保持不變，而車內聲壓級隨之增加，但不同工況下聲壓級受風速影響而變化的頻段不同。對全鋁窗、前玻璃窗和右側玻璃窗而言，風速增加對其聲壓級的影響集中在1 200 Hz 以下；1 200～4 000 Hz 之間，聲壓級波動很小。對全玻璃窗和左側玻璃窗來說，聲壓級在全頻段上均隨風速增加而增長，但增長幅度隨頻率增大而減小，在1 200 Hz 附近，全玻璃窗受前玻璃窗和右側玻璃窗突變的影響，其隨風速變化的趨勢有明顯波動。

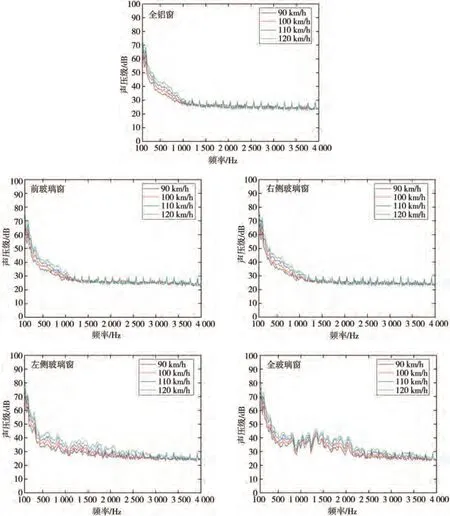
圖8 不同工況下測點噪聲頻譜圖

（2）各窗對內部噪聲的貢獻度分析

120 km/h 風速下，各玻璃車窗工況的頻譜圖如圖9 所示。由圖可知，右側與前玻璃窗的頻譜曲線基本一致，僅在100～800 Hz 頻段內右側玻璃窗的聲壓級略高于前玻璃窗；左側玻璃窗的頻譜曲線在全頻段內均與全玻璃窗相似，僅在1 000～2 500 Hz 之間存在差異，但對總聲壓級影響有限，兩者總聲壓級相差0.89 dB，仍十分接近；全頻段內，左側玻璃窗頻譜曲線高于前玻璃窗和右側玻璃窗，在1 000～2 500 Hz以內，尤為明顯。由此可知，針對測點噪聲聲壓級，各窗的貢獻度依次為：左側窗＞右側窗＞前風窗。

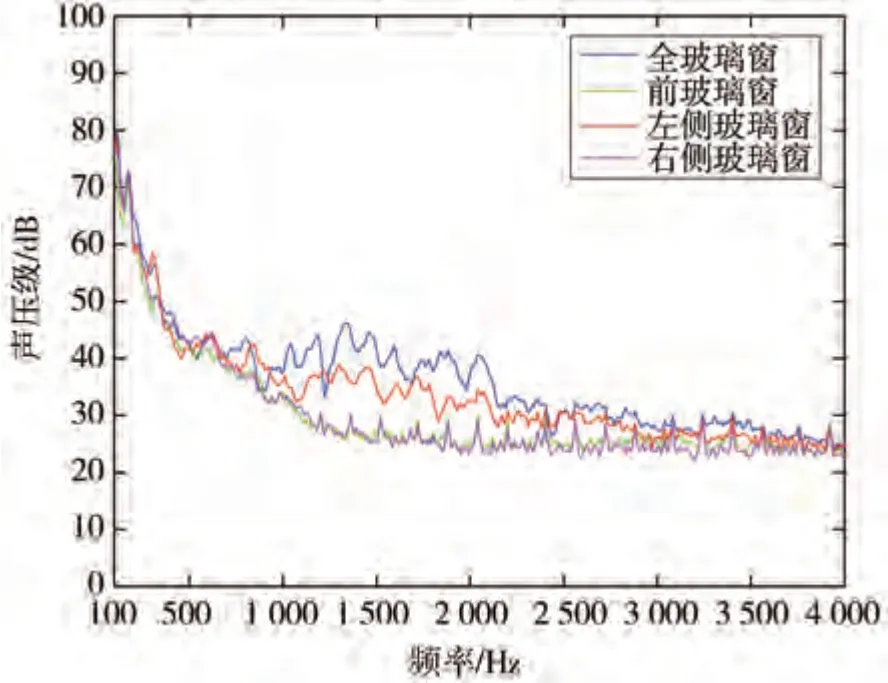
圖9 各玻璃車窗工況的頻譜圖

（3）傳聲效率差異分析

全鋁窗與左側玻璃窗的頻譜圖如圖10 所示。由圖可知，除400～800 Hz 頻段外，其余頻段上左玻璃窗的聲壓級均高于全鋁窗，在1 000 Hz 以上的中高頻段內，這一現象尤其明顯。由此說明，在全頻段內（除400～800 Hz 外），NCT_1 對車內測點的傳聲效率低于NCT_2。

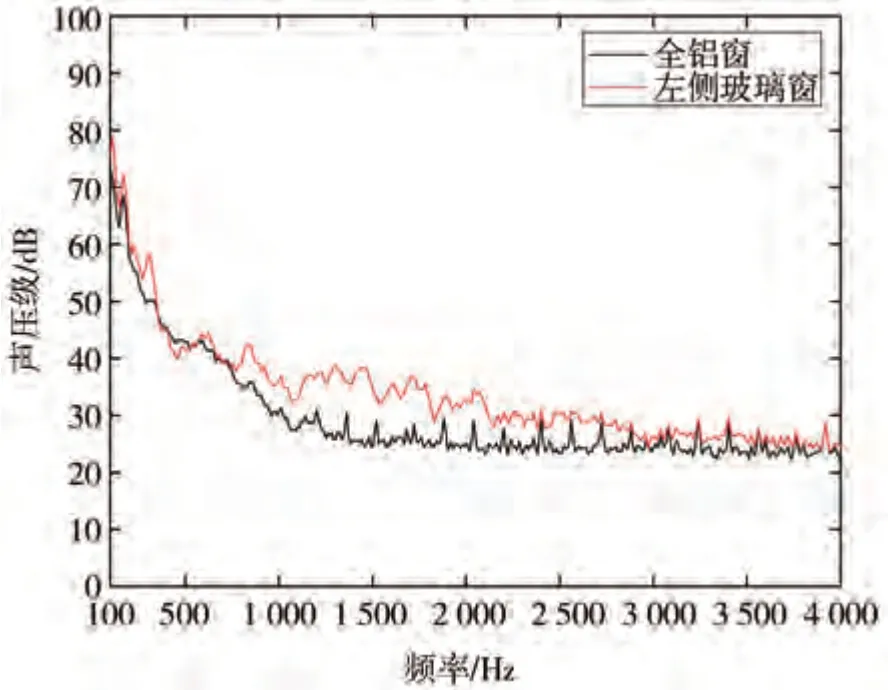
圖10 NCT的傳聲效率對比

結合文獻研究可知，駕駛室內部噪聲主要來源于汽車側窗區域?；趯嶒灧治隹傻茫涸谧髠炔ＡТ肮r下，車體和其他車窗對測點噪聲的貢獻可以忽略，且左側窗下的內部噪聲情況與全部聲源存在下的內部噪聲較為接近。因此研究駕駛員左耳位置處的噪聲水平時，只以左側玻璃窗作為聲源合理可行。而針對400～800 Hz 之間可能帶來的誤差，由于其聲壓級較低，對總聲壓級影響較小，因此誤差應在可接受范圍內。

1.3.3 混響時間測量數據處理

根據文獻［7］處理混響實驗數據，得到HSM 標準模型的混響時間。由計算流體等效阻尼系數，將其作為聲速的虛部，為聲學仿真提供聲學計算參數，聲速設置如表1所示。

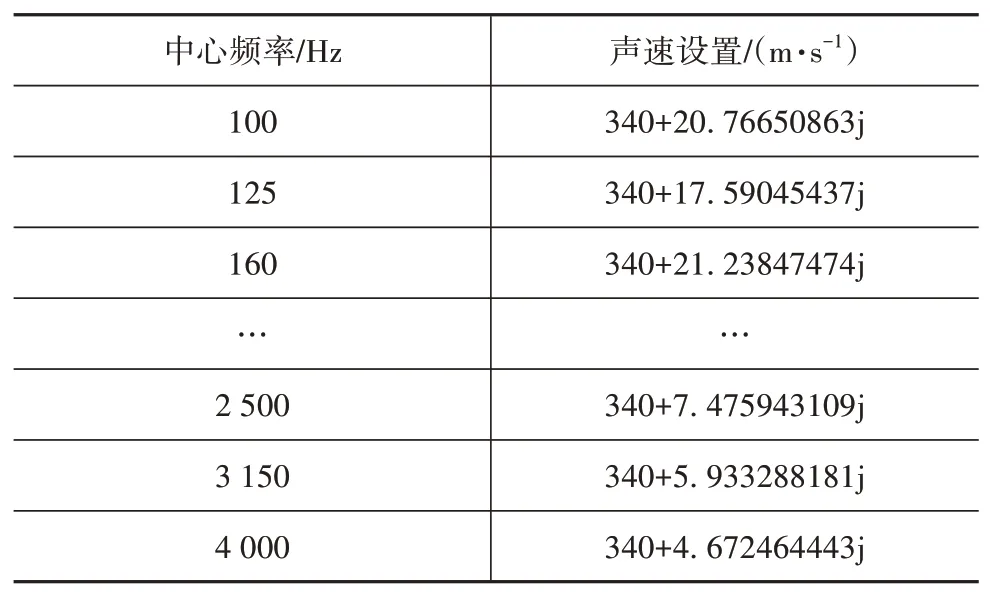
表1 聲腔內部流體聲速設置

2 流場仿真

采用計算氣動聲學方法進行流場仿真求解，研究內部噪聲的成因，并與實驗對比驗證流場仿真準確性。

2.1 流場仿真模型與計算設置

由于計算資源和時長的限制，同時考慮到HSM標準模型本身具有對稱性，故流場仿真中僅使用HSM 標準模型的左半側作為仿真模型。流場仿真模型及監測點如圖11所示。

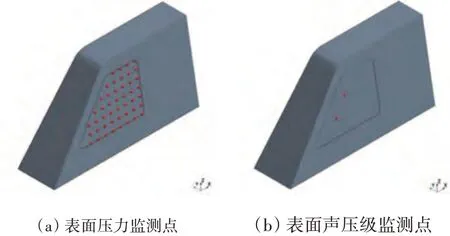
圖11 流場仿真模型及監測點布置示意圖

流場仿真計算域及加密區設置如圖12 所示。計算域的阻塞比為3.3%，滿足仿真要求。采用切割體網格和棱柱層網格劃分計算域，加密區尺寸依次為2、4、8、16和32 mm。

圖12 流場仿真計算域及加密區

流場仿真時首先通過穩態計算以初始化流場，為后續計算提供初始值，然后進行瞬態計算，采用直接計算氣動噪聲法求解，同時計算流場壓力和聲場壓力。時間步長Δ為1.25 × 10s，計算時間為0.2 s，0.1 s后開始采樣。本文邊界條件與求解設置如表2～表4所示。

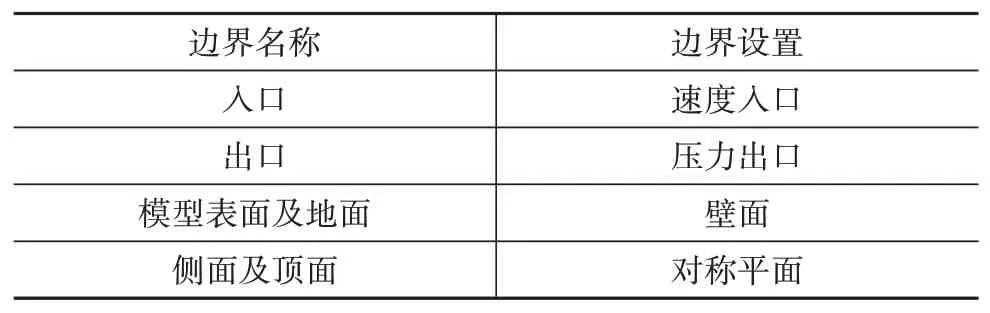
表2 邊界條件設置

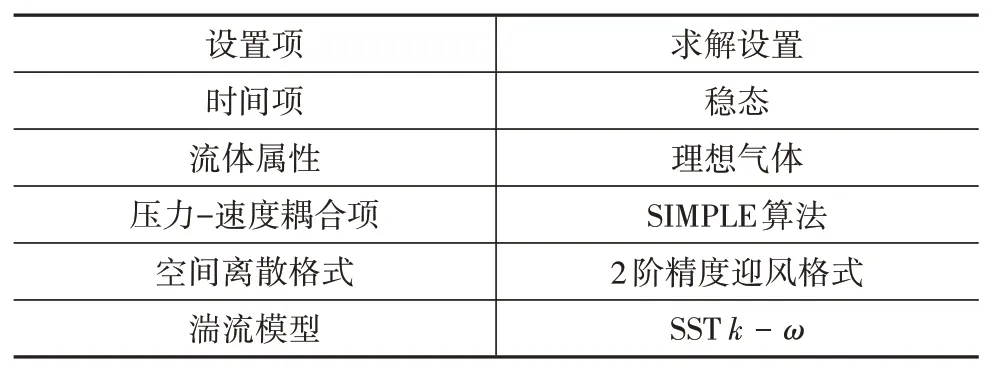
表3 穩態求解設置

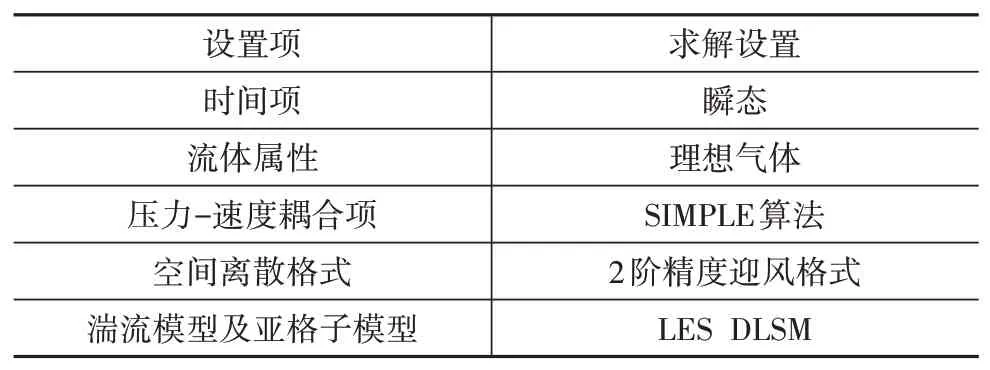
表4 瞬態求解設置

2.2 流場仿真分析

2.2.1 流場結構分析

方法為第二代渦識別方法，可識別流場渦結構?；贑auchy-Stokes分解，表達式為

式中、分別為速度梯度張量的對稱與反對稱部分。

圖13為等值面圖（=800000.0 s）。由圖可看出渦的分布與結構。來流受到HSM 標準模型前緣的阻礙而分離，產生分離渦，該渦隨氣流向后發展一段距離后，重新附著在模型表面。分離渦的存在區域隨向升高，逐漸朝向擴展，其再附著位置也隨著向升高朝向延伸，形成一條傾斜的再附著線。仿真得到再附著線與水平方向約呈30°，如圖13 所示。與實驗結果吻合度較高。由此說明仿真所獲得的流場結構準確性較高。

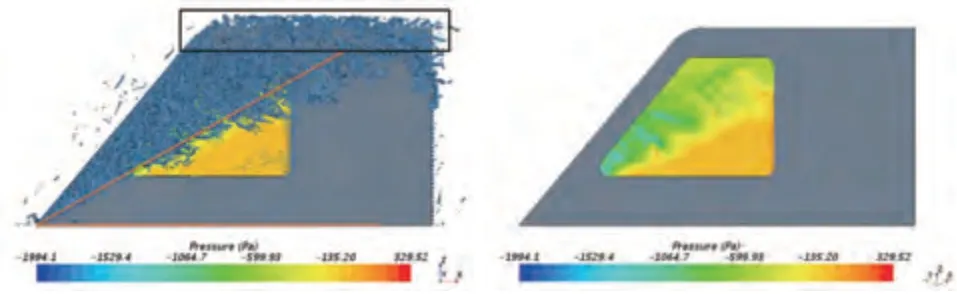
圖13 Q等值面圖及側窗壓力云圖

由圖13 可知，模型前緣分離現象隨向升高逐漸減弱，當氣流遇到弧形過渡時，這部分氣流并不在過渡位置發生明顯分離，而是繼續向后發展與頂部側邊作用產生向側面發展的渦結構，如圖13 黑色區域所示。從圖中可明顯看出，黑色區域的渦結構在強度上不如前端產生的分離渦，且作用區域基本沒有進入側窗，而分離渦的范圍則占據了側窗的左上部分。從壓力云圖可以看出，側窗表面左上部分和右下部分之間存在較大的壓力梯度，側窗表面壓力脈動劇烈，中間的壓力分界線與分離渦再附著線基本一致，這說明側窗表面劇烈的壓力脈動是由模型前緣的分離渦引起。綜上可知，通過側窗向內傳遞的噪聲主要由分離渦引起。

2.2.2 流場聲源分析

對于汽車氣動噪聲，偶極子和四極子聲源為主要噪聲源，因此基于寬帶噪聲源模型對聲源進行分析。

（1）偶極子聲源分析

在假定各向同性的湍流場內，Curle 模型可以計算偶極子聲源產生的聲音，如圖14 所示。由圖可知，在HSM 標準模型側面靠近前緣的位置，存在一傾斜向上的強聲源分布，聲功率強度在100 dB 左右，且越靠近模型底部，強度越高，為主要偶極子聲源。該聲源的位置與上述分離渦再附著位置基本一致。由此可知，該處聲源是由分離渦再附著引起模型表面劇烈壓力脈動而產生的。

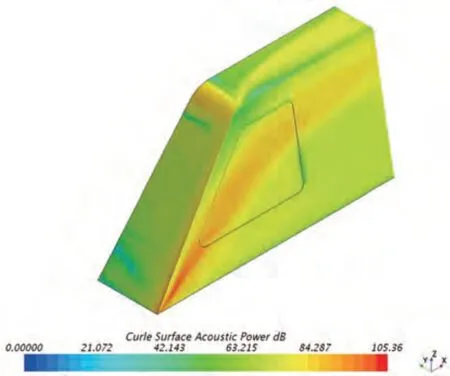
圖14 HSM標準模型表面Curle聲功率分布云圖

（2）四極子聲源分析

在假定各向同性的湍流場內，Proudman 模型可以評估流場中湍流產生的四極子聲源造成的局部影響。圖15 為湍流結構在HSM 標準模型的不同向位置的流場內產生的四極子聲源。由圖可知，在同一水平面上，四極子聲源朝和向擴散，且以向為主要傳播方向，隨向的增大，四極子聲源作用范圍在和向上擴展，但仍以向為主，且聲源強度的核心區也隨向增加逐漸朝向移動，但聲源強度隨向增加而減小。根據四極子聲源作用范圍終止點的遷移可以看出，四極子聲源在模型側面產生了傾斜向上的作用區，隨向升高，作用范圍增大，作用強度減弱，這一現象與模型前緣分離渦的效果一致。由此可知，四極子聲源是由分離渦引起模型側面前端附近的渦流運動劇烈而產生的。

圖15 HSM標準模型表面Proudman聲功率分布云圖

綜上所述，模型前緣產生的分離渦及其再附著現象是車內噪聲的主要成因。

2.3 流場仿真結果驗證

通過仿真計算得到表面壓力監測點的瞬態結果，將其平均后與各測點的表面壓力實驗數據進行對比，結果如圖16 所示。由圖可以明顯看出，仿真結果與實驗數據具有一致性。

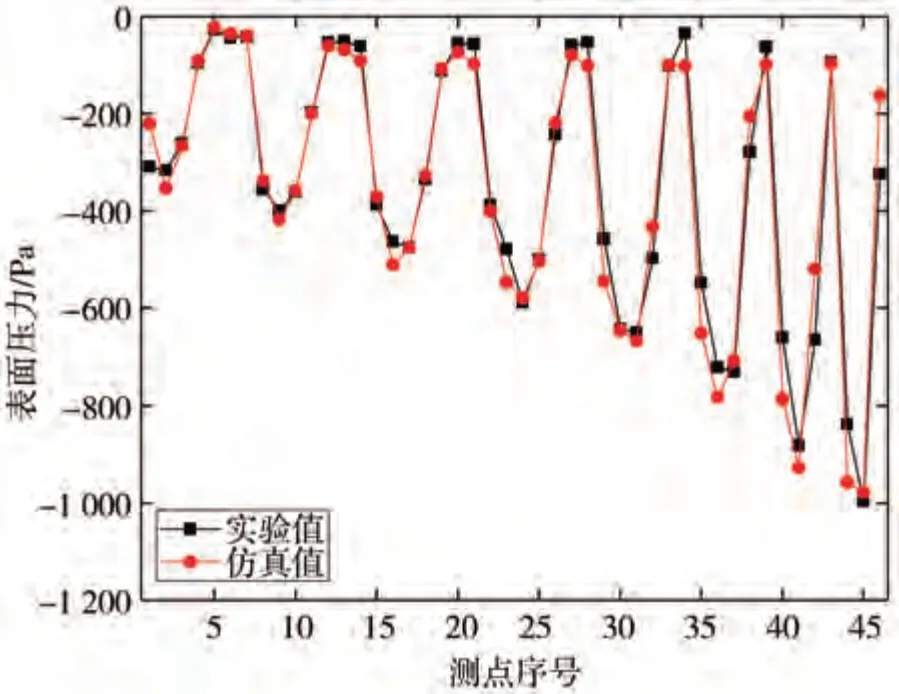
圖16 表面壓力實驗與仿真對比圖

將仿真計算得到表面聲壓級監測點的瞬態結果，經傅里葉變換得到1/3倍頻程曲線。鑒于本次實驗條件的限制，未能對側窗外表面的聲源信息進行測量，因此選擇HSM 標準模型實驗的文獻［10］進行表面聲壓級的驗證。實驗與仿真的對比結果如圖17 所示。從圖可以看出，仿真結果與參考實驗數據具有良好的一致性，各中心頻率下的差異在10%以內。

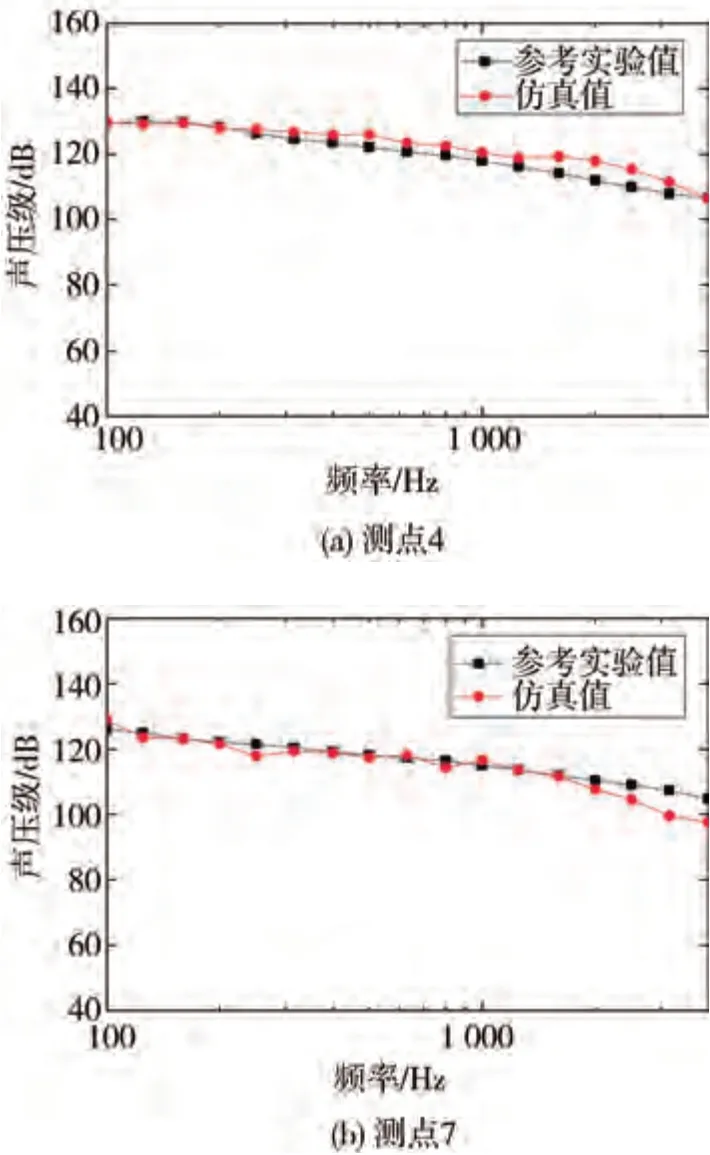
圖17 表面聲壓級實驗與仿真對比圖

由以上對比結果可以說明，本文中采用的流場計算方案具有較高準確性。

3 聲場仿真

采用ACTRAN 聲學求解器對HSM 標準模型進行內部聲傳播計算，并與實驗對比驗證聲場仿真準確性。

3.1 聲場仿真模型與計算設置

根據實驗模型的內部聲腔建立聲場仿真所用的聲腔模型，內部監測點與實驗測點保持一致，聲場仿真模型及監測點的布置如圖18所示。

圖18 聲場仿真模型及監測點

聲場計算時，為保證聲傳播的計算精度，聲腔模型的體網格尺寸與求解頻率應滿足：

上式表示目標求解頻率所對應的一個聲波波長應包含6～8 個網格，其中為聲速，Δ表示聲腔模型的最小網格尺寸。

本文目標求解頻率為4 000 Hz，綜合求解精度和計算時長考慮，聲場仿真模型上聲源加載區網格尺寸為2 mm，網格節點與流場仿真模型一一對應。聲場仿真的計算設置如表5所示。

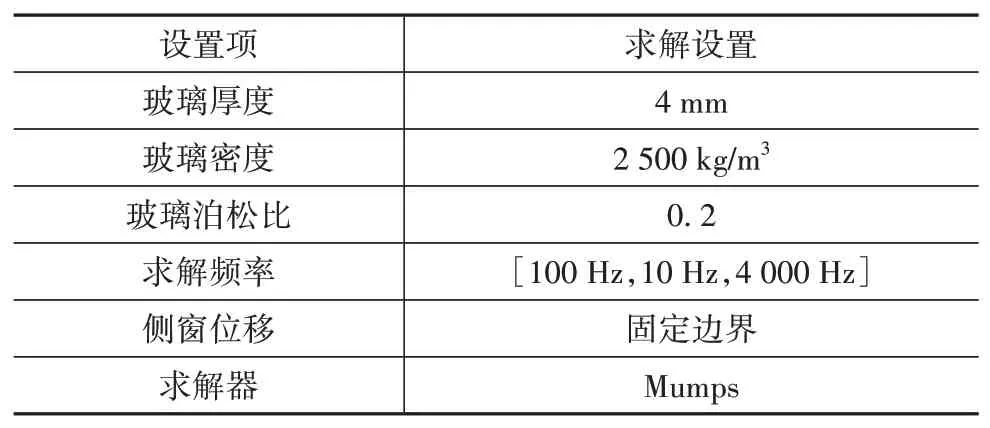
表5 聲場仿真計算設置

3.2 聲場仿真分析

3.2.1 聲源激勵成分分析

定義5[1,7] 設μ:X∪Y→X∪Y上的映射，若N>M≥2，對任意的Xi∈X,Yj∈Y，滿足：μ(Xi)∈Y,μ(Yj)∈X∪{Yj}和μ(Xi)=Yj,μ(Yj)=Xi，則Xi和Yj在μ中匹配，稱(Xi,Yj)為雙邊匹配對。若(Xi,Yj)是μ中任意的雙邊匹配對，且μ(Xi)≠Yj′,Yj′∈Y,Yj′≠Yj,μ(Yj)≠Xi′,Xi′∈X,Xi′≠Xi，則稱μ是一對一雙邊匹配，μ(Yj)=Yj表示Yj在μ中未匹配。

流場計算得到的聲源激勵由兩種成分組成：一是流場中渦結構本身作為聲源，向周圍輻射聲波，這種聲源激勵被稱為聲學壓力脈動（acoustic wall pressure fluctuation，AWPF）；另一種是流場中流體與結構直接作用，引起結構邊界發生振動而形成的聲源，被稱為湍流壓力脈動（turbulent wall pressure fluctuation，TWPF）。

表面壓力激勵由PMD 分解得到圖19。由圖可知，湍流壓力脈動與側窗表面壓力脈動基本重合，隨著頻率的升高，差異逐漸顯現，但差距始終較小，而聲學壓力脈動在全頻段上，數值遠小于湍流壓力脈動，兩者之間的差距隨頻率升高而減小。由此說明左側窗上的聲源激勵，主要成分是湍流壓力脈動，其占比隨頻率增大而減小，但始終維持在一個較高的水平。

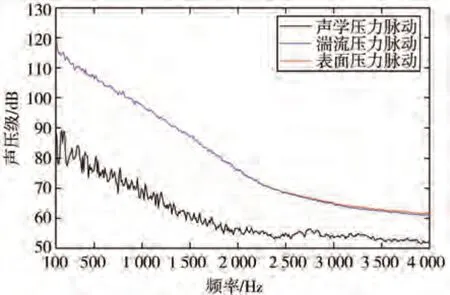
圖19 左側窗表面壓力分解結果

3.2.2 內部噪聲源項貢獻度對比

圖20為表面壓力及不同壓力脈動分別加載得到的內部噪聲頻譜圖。由圖可知，表面壓力脈動產生的內部噪聲在低頻段時，受聲學壓力脈動與湍流壓力脈動的共同作用，隨著頻率的升高，聲學壓力脈動逐漸占據主導地位，湍流壓力脈動的貢獻越來越小。在2 500～4 000 Hz 內，表面壓力脈動的頻譜曲線基本與聲學壓力脈動產生的內部噪聲一致。由此說明，內部測點的噪聲主要來自聲學壓力脈動，其占比隨頻率的升高逐漸增加，在高頻段內的內部噪聲基本由聲學壓力脈動造成。

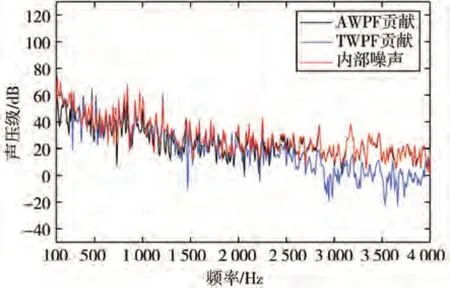
圖20 內部噪聲貢獻對比圖

3.2.3 傳遞效率對比

綜上所述，聲源激勵和內部噪聲的主成分完全相反，這是側窗玻璃對不同聲源激勵的傳遞效率不同所致。

根據研究人員對板隔聲量的研究發現，單層薄板在外部激勵發生受迫振動時，會在板內產生彎曲波，當外部激勵達到某頻率時，彎曲波的波長在激勵波方向上的投影等于激勵波的波長，此時兩種波發生共振，激勵波以高傳遞效率通過薄板，這一現象被稱為吻合效應。

由此可知，當聲源激勵的波數與彎曲波波數相近時，受激勵引起的玻璃彎曲波波長與激勵波波長接近，易引起共振，此時玻璃對該激勵波的傳遞效率較高。為此，計算各頻率下聲源激勵及側窗玻璃波數之間的關系，公式如下：

式中：為湍流壓力脈動的波數；為對流速度。

式中為聲學壓力脈動的波數。

式（3）表示湍流壓力脈動對應波數與頻率的關系。式（4）表示聲學壓力脈動對應波數與頻率的關系。

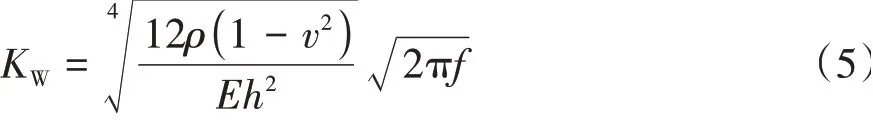
上式表示玻璃受激勵后產生的彎曲波波數，以無限大平板的波數求解公式進行近似求解。式中、、、分別表示玻璃的彈性模量、厚度、泊松比和密度。經計算得到如圖21所示的波數-頻率圖。

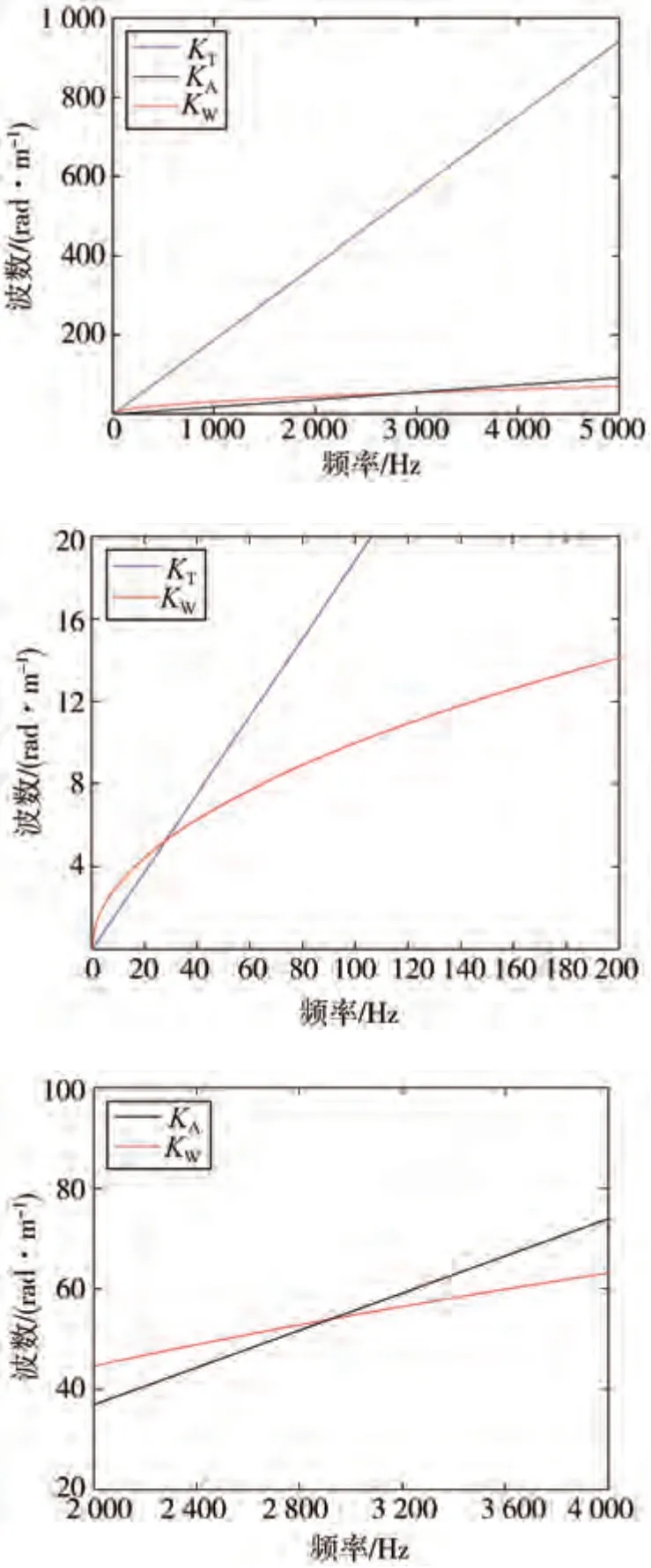
圖21 聲源激勵及側窗玻璃的波數-頻率圖

由圖可知，全頻段內聲學壓力脈動的波數與側窗玻璃彎曲波的波數相近，即聲學壓力脈動在全頻段上與玻璃彎曲波波長接近，因此聲學壓力脈動通過側窗玻璃的傳遞效率較高，激勵作用較明顯。而湍流壓力脈動的波數只在低頻段內較為接近，在耦合頻率以上，波數與彎曲波相差甚遠，即湍流壓力脈動僅在低頻段內與彎曲波波長相近，因此湍流壓力脈動通過側窗玻璃的傳遞效率隨頻率升高而降低，激勵作用并不明顯。正是這樣的傳遞效率差異導致了聲源激勵與內部噪聲在主成分上完全相反的結果。

3.3 聲場仿真結果驗證

將聲場仿真得到的頻譜曲線與實驗結果進行對比，如圖22 所示。由圖可知，實驗與仿真結果的聲壓級隨頻率變化的趨勢基本一致，除400～800 Hz外，各頻率所對應的聲壓級在數值上差距較小?？偟膩碚f，實驗與仿真整體一致性較好。其中400～800 Hz 的誤差較其他頻段明顯，原因如1.3.2 節所述，該頻段內不同NCT 的傳遞效率差異不足以忽略其他聲源作用，因此產生仿真誤差。綜上所述，本文中采用的流場-聲場聯合仿真具有較高準確性。

圖22 內部噪聲實驗與仿真對比圖

4 結論

基于HSM 標準模型的實驗與仿真分析，得到如下結論。

（1）隨風速增加，不同聲源作用下的內部噪聲在不同頻段上變化規律不同。全鋁窗、前玻璃窗和右側玻璃窗作用下，聲壓級主要在1 200 Hz 以下隨風速有明顯變化，全玻璃窗和左側玻璃窗作用下，聲壓級在全頻段上隨風速增加而增加，但增長幅度隨頻率增大而減小。

（2）模型前緣分離渦及其再附著引起的壓力激勵由各窗向內傳遞產生內部噪聲，各窗對內部噪聲的貢獻大小為：左側窗＞右側窗＞前風窗。經實驗驗證，以左側窗為唯一聲源可獲得與全部聲源存在時相近的聲壓級結果，因此針對駕駛員左耳位置的噪聲研究，可以只考慮左側窗聲源。

（3）表面壓力激勵包含湍流壓力脈動和聲學壓力脈動，湍流壓力脈動是聲源激勵的主成分，占比隨頻率升高而降低。聲學壓力脈動是內部噪聲的主成分，占比隨頻率升高而增大。兩者的差異是由玻璃對兩種聲源的傳遞效率不同引起的，這是不同激勵與玻璃彎曲波之間不同波數關系導致的。