基于交互式多模型平方根容積卡爾曼濾波的船舶軌跡跟蹤

楊家軒，陳柏果，馬令琪

1 大連海事大學 航海學院，遼寧 大連 116026

2 遼寧省航海安全保障重點實驗室，遼寧 大連 116026

0 引 言

智能航運是海運業未來的發展方向，船舶在航行的過程中要求其能自主探測其他船舶并采取適當的規避措施。探測其他船舶的移動，可以使用各種導航傳感器，如自動識別系統（AIS）、航海雷達和激光雷達。其中，AIS 適用于所有300 總噸以上的船舶和許多小型船舶，其允許船舶廣播自己的位置、航向和時間數據，并接收附近其他船舶的信息，可提高海上航行的安全和效率。同時，由于AIS 是通過甚高頻無線電頻率來進行傳輸，即使是在雷達探測受到威脅的惡劣環境中，其也能繼續探測其他船舶，因此，AIS 被廣泛用于電子海圖集成顯示、船舶的監控調度、港口交通流規律的挖掘等領域。

然而，若要通過AIS 獲取準確、可靠的信息，特別是實時位置和航速等動態信息，仍然存在一些問題。Bany?等[1]針對實際情況下AIS 數據的長期分析表明，因AIS 中的部分數據被設置為默認值，或其數據幀嚴重違反指定的更新速率，導致許多AIS 消息中包含有不可信的位置坐標。此外，AIS 的參數，如航向或航速有可能是由錯誤的位置估計得出，從而導致了虛假的船舶動態狀態信息。

AIS 最初被設計為僅用于交換靜態數據和導航數據，不提供任何完整性信息，因此不能確保服務的連續性。AIS 信息有時會被部分或完全中斷，并且因“數據干擾”問題導致的數據丟失在高流量區域可能會更嚴重[2]。

目前，卡爾曼濾波（KF）算法常被用來進行機動目標的跟蹤和導航，如擴展卡爾曼濾波（EKF）[3]、無跡卡爾曼濾波（UKF）[4]、容積卡爾曼濾波（CKF）[5]等。為確保AIS 信息的可靠性以及數據的精度，可以采用卡爾曼濾波算法對AIS 數據進行處理。Jaskólski[6]采用傳統的KF 算法估計了AIS 報告的位置坐標，但該方法僅適用于船舶航行的線性環境，在非線性情況下（如轉彎操作）會產生錯誤警報。Perera 和Soares[7]采用恒定轉向率模型（CTM）作為非線性狀態估計量，假設船舶處于勻速狀態，結合EKF 算法對船舶處于非線性環境下的航行軌跡予以了估計。Fossen 等[8]采用EKF 算法處理AIS 的實時數據，并將其用于了碰撞檢測和實時可視化，但基于EKF 的預測算法只能考慮單一的船舶運動模型，難以描述變換狀態的船舶運動。Fossen 等[9]又將船舶全局運動參數加入系統狀態方程中，通過構建eXogeneous 卡爾曼濾波器（XKF），完成了對船舶運動模式的實時預測，但該模型在近180°的機動角度下預測軌跡存在較大誤差。針對AIS 數據呈現的多機動性和運動模式多的問題，姜佰辰等[10]采用多項式卡爾曼濾波對數據進行了處理，但算法的軌跡跟蹤效果取決于多項式的階數，且缺乏性能的對比標準。Siegert 等[11]將交互式多模型（IMM）框架用于混合恒速過程模型和恒定轉向率過程模型的狀態估計，并結合EKF 算法對船舶的非線性狀態估計進行了處理。但在采用EKF 對非線性函數進行近似化處理的過程中會引入較大誤差，這對于強非線性濾波問題來說容易發散，故一般用于非線性程度低且初始誤差較小的系統[12]。Liu 等[13]設計了一種使用KF和IMM 的智能魯棒跟蹤算法，該算法在受限的環境下依然能夠利用AIS 數據中不完整的動態信息計算出精確的運動信息。于澤祥等[14]采用交互式多模型-平方根容積卡爾曼濾波（ IMM-SCKF） 算法對海上擴展目標進行跟蹤濾波，通過擴展信息，提高了算法的跟蹤精度。但以上采用IMM 框架的方法沒有考慮船舶或運動目標航速的變化及航向率的變化，對目標運動的描述還不夠全面和準確。

在采用AIS 數據進行跟蹤和預測的KF 算法中，使用較為廣泛的是EKF 算法，但在船舶航向和航速變化較頻繁的軌跡跟蹤場景下，采用EKF算法會引入較大的誤差。針對EKF 算法的穩定性問題，本文將引入一種更具數值穩定性的SCKF算法來進行AIS 數據的軌跡跟蹤。根據船舶航向和航速的變化，可以劃分出直線運動、轉向運動和變速運動3 種基本運動狀態，船舶的運動可以看作是這3 種運動狀態的變換與組合。對于涉及這3 種運動狀態的船舶軌跡，采用單一運動模型無法準確擬合和描述。而IMM 算法可以將多個模型進行融合并自適應轉換表征目標的運動狀態，因此，本文擬將SCKF 算法和IMM 框架相結合，通過IMM 框架對單一運動模型進行組合。首先，采用恒速直線模型（CVM）和恒定轉向率模型（CTM）交互融合形成的組合模型與單一模型進行比較，驗證IMM 框架的性能；然后，考慮軌跡航向的變化，采用轉向率估計值來替代固定轉向率以形成改進的CTM 模型，通過CVM 與改進的CTM 形成組合模型，分析改進的CTM 模型性能及其對存在轉向率變化的船舶運動的表征能力；最后，針對存在直線運動、轉向運動和變速運動的軌跡，采用CVM、當前統計模型（CSM）和改進的CTM 模型三者融合形成的組合模型進行跟蹤實驗，通過實驗對比EKF和SCKF 算法的性能，分析不同組合模型的性能和使用場景，以驗證本文算法對涉及2 種以上運動狀態的船舶軌跡跟蹤結果的準確性和穩定性，從而提高AIS 的服務質量。

1 AIS 數據的單位轉換

AIS 數據包含對地航速V、對地航向φ以及地理位置的經緯度 (l, μ) 。 為便于計算，可將航速V的單位由kn 轉換為 m/s。目前，AIS 數據的經、緯度是采用大地測量系統（WGS84）坐標系來進行記錄，將經、緯度坐標映射為笛卡爾坐標 (x,y)。最后，坐標將使用二維笛卡爾坐標系來表示。

假設地球平面坐標原點位于經緯度(l0, μ0)處，并定義

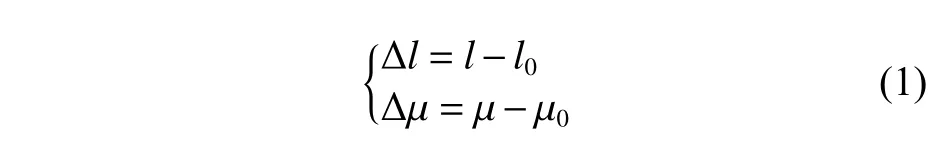
地球在垂直主子午線上的曲率半徑RN和在子午線上的曲率半徑RM由式(2)表示：

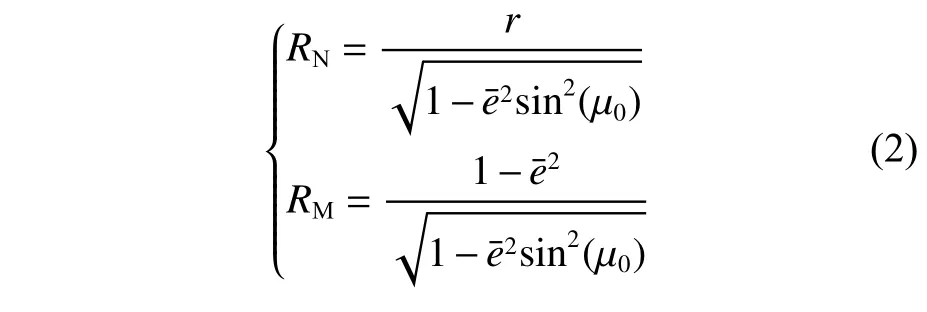
式中：r為半短軸（赤道半徑），r=6 378 137 m；eˉ 為地球偏心率[8]，eˉ=0.081 8。笛卡爾坐標系下的位置 (x,y)的計算如下：

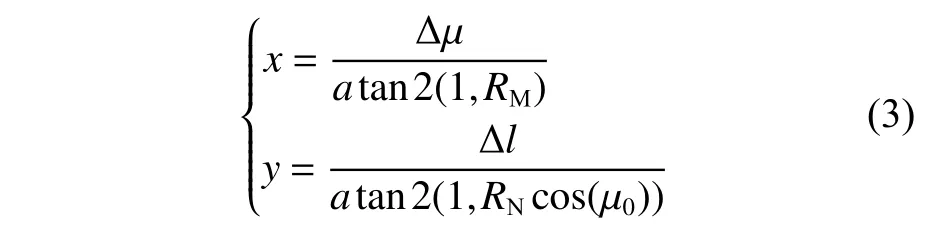
式中，atan2(y,x)為四象限反正切，將結果限制在[-π,π]范圍內。

2 船舶運動模型

由于大多數船舶既沒有很強的機動性，也不能在一定的采樣周期內快速改變改變航速，因此，使用簡單的運動模型來表示船舶的運動是合理、可行的。在模型選擇過程中，考慮了能夠捕捉船舶運動能力的二維運動學模型[7]。假設船舶是一個質點，忽略其尺寸。如圖1 所示，船舶位于點A 處，船舶的位置坐標由連續時間內的x和y來表示；vx，vy為 船舶沿X，Y方向的連續時間速度分量；v為船舶的航速；v˙為船舶航速的變化率； 假設船舶對地航向與船艏航向一致，則 ω為船舶航向的變化率；x(t),y(t)為 船舶在笛卡爾坐標系下時間t處的位置；an，at分別為船舶的法向加速度和切向加速度[7]。

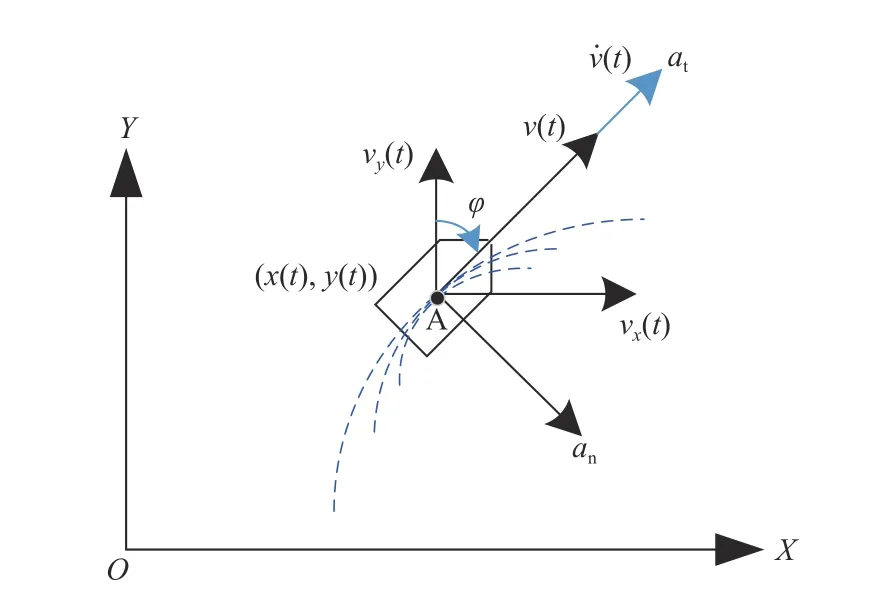
圖1 船舶運動模型示意圖Fig. 1 Schematics of ship motion model

曲線運動模型可用于描述船舶運動：

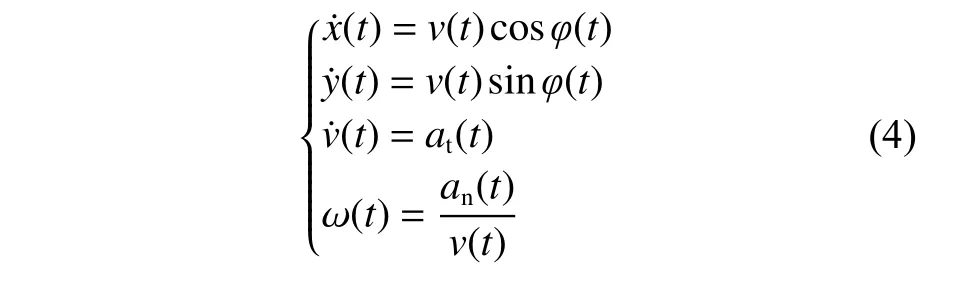
式中， ω(t)為 船舶在笛卡爾坐標系下時間t處的航向變化率。從該船舶運動模型中，可以觀察到一些重要的運動特征。基于式(4)，可推斷有3 種不同的運動狀態：

1）an(t)=0,at(t)=0，直線勻速運動；

2）an(t)=0,at(t)≠0，直線變速運動；

3）an(t)≠0,at(t)=0，轉向勻速運動。

當an和at均為0 時，船舶勻速直線運動。假設航速在第k個采樣周期內有一個恒定值，則CVM模型將被用來描述船舶的直線勻速運動。設采樣周期為T，則CVM 模型的離散狀態方程為[15]：

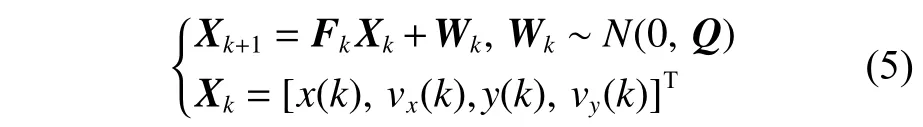
其中：

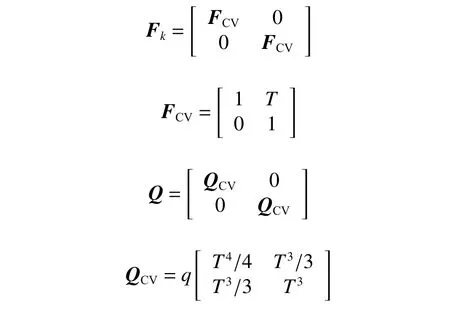
式中：Xk為 狀態向量；Fk為 狀態轉移矩陣；Wk為過程噪聲，其服從均值為0、協方差矩陣為Q的正態分布；q為過程噪聲的協方差系數。

當an(t)=0,at(t)≠0時，船舶直線變速運動。本文采用CSM 模型來表示船舶的直線變速運動。CSM 模型是一種非零均值時間相關的模型，其假設目標以某一加速度機動時，下一時刻的加速度取值范圍有限，且總在“當前”加速度值的附近。這種對于船舶航速變化狀況的描述是較為合理的。CSM 模型的離散狀態方程為[15]：

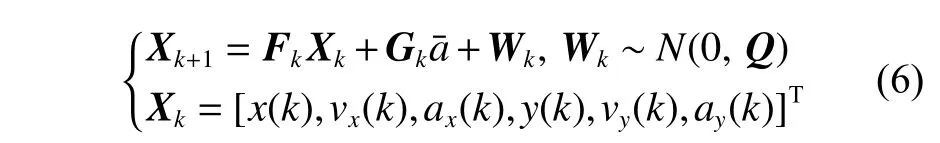
其中：

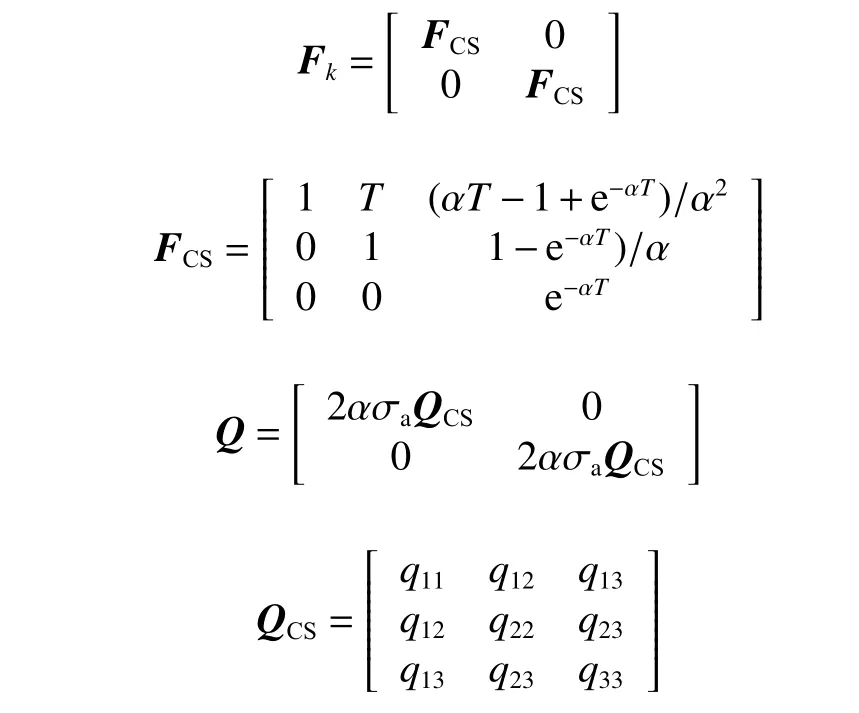
式中：ax(k)，ay(k)分 別對應于X，Y軸方向上的加速度；aˉ為 加速度的均值，通過矩陣Gk進 行更新； α為機動時間常數；q11～q33的表達式參見文獻[7]；σa為加速度的方差。

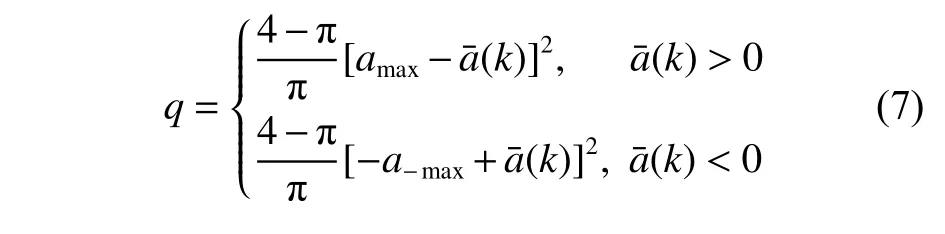
式中：amax為目標的最大正向加速度；a-max為目標的最大負向加速度；aˉ(k)為加速度的均值，當前加速度的均值取加速度的估計值。

當an(t)≠0,at(t)=0，時，船舶進行圓周勻速運動，也即轉向運動。假設在第k個采樣周期內船舶的航速和角速度恒定，此時船舶的運動過程適合采用CTM 模型來描述。CTM 模型的離散狀態方程為[15]：

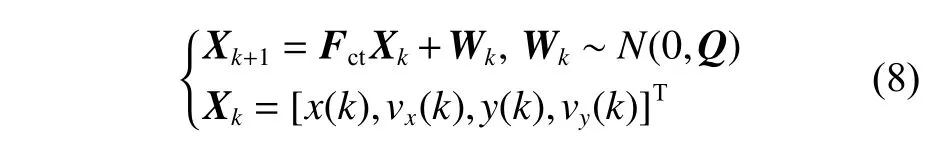
其中：

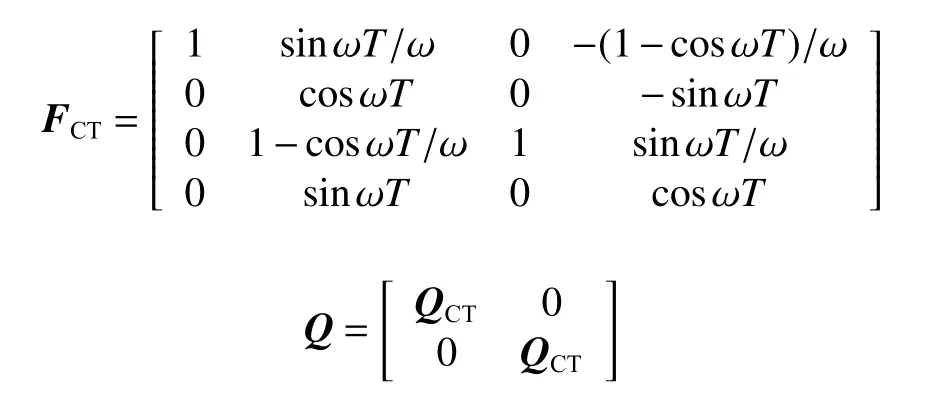
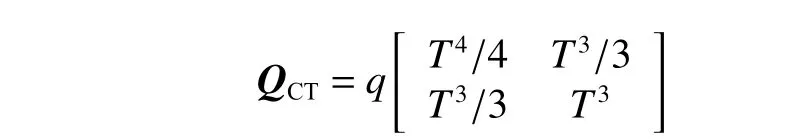
式中， ω為航向的變化率。

CTM 模型性能受轉向率的影響較大。在準確了解轉向率的情況下，CTM 模型能提供良好的跟蹤性能。在極少數情況下，恒定的轉向率是預知的，但在大多數實際情況下，直接使用CTM 模型不現實。因此，一個自然的想法就是用其估計值 ω?來代替。需要注意的是，應當篩選估計值以降低異常值的影響。利用飽和函數 sat(ω)來確保|ω?|≤ωmax，以防止估算的轉向率超出轉向率最大值 ωmax，可增加AIS 測量數據的魯棒性。

3 基于AIS 的船舶軌跡跟蹤算法

3.1 SCKF 算法

在自主或輔助導航領域，KF 算法已經得到廣泛的研究和應用。而EKF 算法則被認為是許多非線性系統應用的標準方法，其能夠使系統關于估計的狀態軌跡線性化。然而，這會導致穩定性問題。另外，在采用EKF 算法對非線性函數進行近似化處理的過程中會引入較大誤差，它只在非線性動態系統與觀測模型的線性近似有效的情況下才表現良好。Duan 等[16]提出了SCKF 算法，該方法是以目標狀態協方差的平方根來進行迭代更新，可確保濾波過程中協方差矩陣的對稱性和半正定性，能夠改善數值的精度和穩定性。本文將SCKF 算法與IMM 框架相結合，能夠對不同維數的模型進行交互濾波，更適合解決船舶在含有多種運動狀態場景下的動態濾波問題。

如圖2 所示，AIS 數據傳輸機制由2 部分組成：數據接收點和數據等待期[2]。導航信息在每個數據接收點傳輸，在數據等待期中則沒有信息的傳輸。并且，AIS 是根據船舶的航速以不同的更新速率來傳輸動態信息的，這會導致不同類型的AIS 數據的數據接收點間隔時間不一致。

圖2 AIS 傳輸機制圖Fig. 2 AIS transmission mechanism

本文中，SCKF 算法的迭代運算過程采用離散時間形式的預測-校正表示法[17]描述。兩個數據接收點之間的采樣時間將隨著船速的增加而自動減少，如果船舶正在做機動航行，信息間隔會進一步減少。因此，可以選擇采樣時間的倍數來作為校正器的更新時間。

船舶過程方程的離散形式可由式(5)、式(6)和式(8)來表示。船舶測量模型的離散形式為：

式中：Zk+1|k為測量的狀態向量；h(Xk+1)為測量函數；Vk為具有零均值和測量噪聲矩陣R(k)協方差的白高斯測量噪聲。

本文所采用的3 種船舶運動模型的測量函數均可采用下式表示：

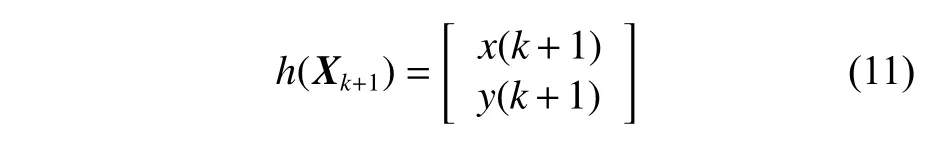
基于過程方程和測量方程，采用預測-校正表示法的SCKF 算法的步驟如下所示。

步驟1：初始化。

步驟2：預測過程。

計算狀態容積點及其對應的權重：

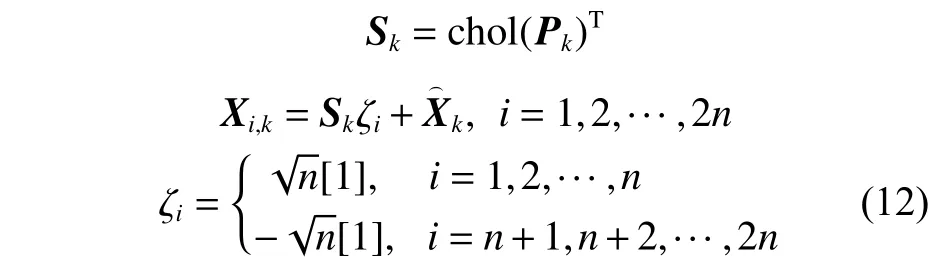
式 中：Pk通 過Cholesky 分 解 得 到 平 方 根Sk； ζi為第i個容積點；n為系統狀態向量的維度； [1]為單位矩陣。每個容積點的權重為。

傳播狀態容積點：

式中：f(Xi,k)為 系統過程函數；Xi,k+1|k為每個容積點對應的預測值。

計算狀態向量預測值：

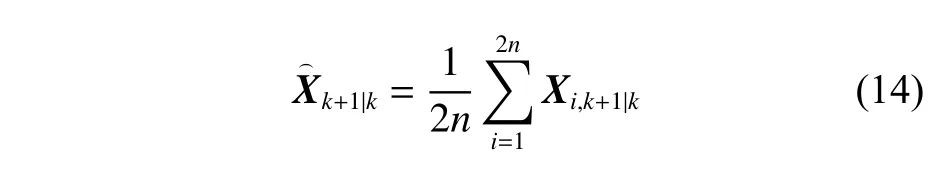
計算狀態誤差協方差的平方根的預測值：

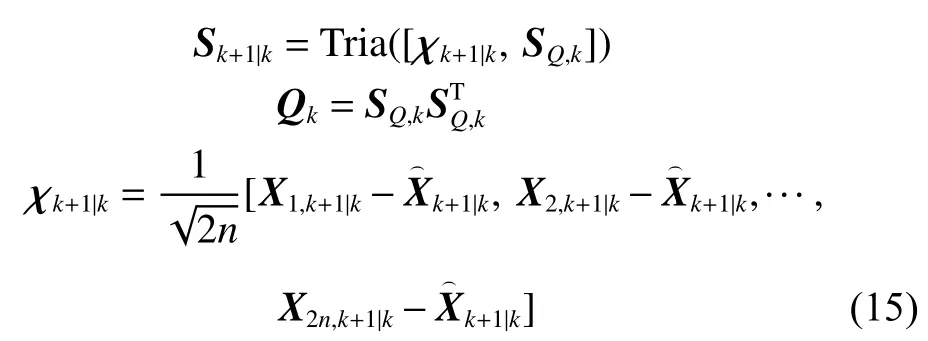
式中：Sk+1|k為一個下三角矩陣； Tria(*)為矩陣的正交三角（QR）分解；Qk為過程噪聲的協方差矩陣，其平方根形式為SQ,k； χk+1|k為狀態向量的偏差矩陣。

步驟3：校正過程。

計算測量容積點及其權重：

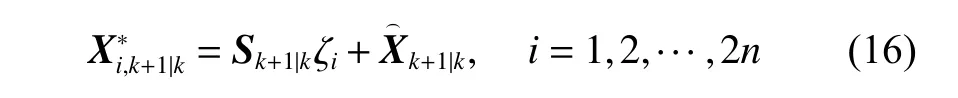
計算通過測量方程傳播的容積點：

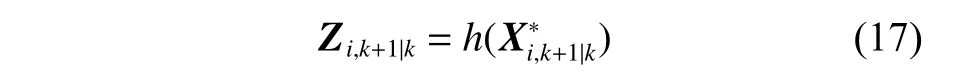
計算測量狀態的預測值：

計算測量誤差協方差的平方根：

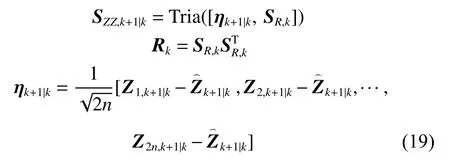
式中：SZZ,k+1|k為新息方差的平方根因子； ηk+1|k為測量向量的偏差矩陣；Rk為測量噪聲的協方差矩陣，其平方根形式為SR,k。

計算互協方差：

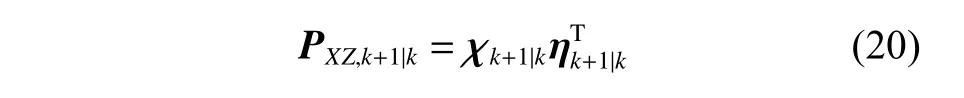
更新卡爾曼增益：

更新狀態值：

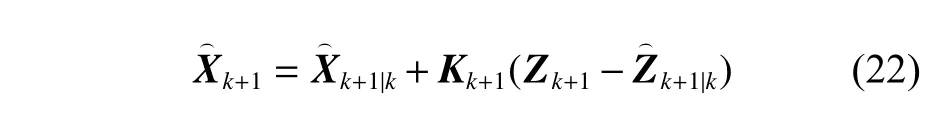
更新狀態誤差協方差的平方根：

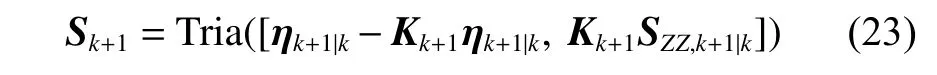
3.2 IMM-SCKF 算法

盡管對所有動態場景只使用一個模型是可以接受的，但若能將不同模型的優勢都融合到一個組合過濾器中，這對復雜船舶運動軌跡的擬合和描述來說效果將更好，能擴展跟蹤算法的適用場景并提高跟蹤算法的穩定性和精度。與其他利用多個模型并行運行的方案形成對比的是，IMM 混合了不同模型的狀態估計，而不用在一個或另一個之間做出艱難的決定。

圖3 描述了IMM-SCKF 算法原理。SCKF 濾波器分別采用CVM，CSM 和改進的CTM 這3 種模型來實現狀態的估計與更新，IMM 框架則將通過濾波器得到的狀態進行交互融合。IMM-SCKF算法的推導步驟如下所示。

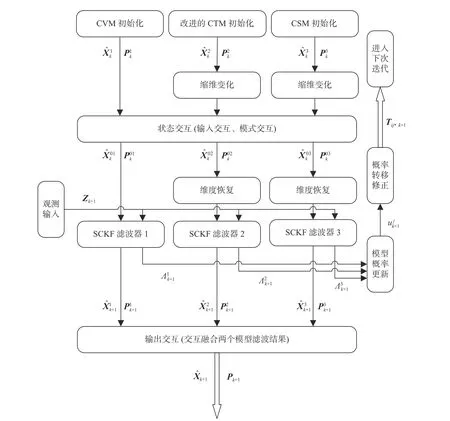
圖3 IMM-SCKF 算法的原理框圖Fig. 3 Block diagram of IMM-SCKF algorithm

步驟1：輸入交互。

考慮N個運動模型，假設上一次迭代運算的第j個模型對應的狀態向量和誤差協方差矩陣分別為以及。在SCKF 算法的每個預測-校正周期之前，通過輸入的交互融合得到第j個濾波器的初始狀態向量和初始誤差協方差矩陣。

步驟2：模型過濾器。

用N個濾波器來表示N個運動模型（本文中，N=3） ，將在步驟1 中獲得的和作為SCKF算法的初始輸入，用k+1時 刻的測量值Zk+1來進行校正。最終，濾波器得到的狀態向量和誤差協方差矩陣的估計分別為和1。

步驟3：更新模型概率。

步驟4：輸出交互。

將濾波得到的結果進行交互融合，從而得到最終的預測結果。

步驟5：更新馬爾可夫概率轉移矩陣。

馬爾科夫概率轉移矩陣Tij,k的變化是建立在模型進行切換的基礎上的，利用運動模型在相鄰時刻的概率差()對概率轉移矩陣進行校正更新。

4 仿真與結果分析

采用每個軌跡點的均方根誤差（RMSE）和N個軌跡點的平均均方根誤差（ARMSE）對算法的預測結果進行評估。基于位置的RMSE和ARMSE的計算如下：

4.1 參數配置

在IMM 框架中，不同運動模型進行交互融合可形成不同的組合模型：CVM 與CTM 的交互結果為組合模型1，CVM 與改進的CTM 交互結果為組合模型2，CVM，CSM 與改進的CTM 交互結果為組合模型3。組合模型中包含有一個馬爾科夫概率轉移矩陣Ti j,k，其反映了不同運動模式下切換的趨勢。

實際的船舶運動是一個連續過程，在當前時刻采用CVM 模型的條件下，下一時刻保持為CVM 模型的概率極大，而轉換為其他模型的概率極小，因此，將狀態轉移矩陣主對角線的值設置為0.9。為體現實驗的對照過程，相同維度的組合模型采用相同的概率轉移矩陣。組合模型1 的狀態概率轉移矩陣用T1|ij,k表示；組合模型2 和組合模型3 的狀態概率轉移矩陣則用T2|ij,k表示如下：

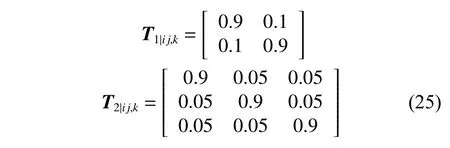
對于每個運動模型，濾波器都需要設置過程協方差Q、測量協方差R以及相關誤差狀態協方差P的初始值P0。 在整個算法的迭代過程中，Q和R被認為是不隨時間變化的參數，而P則需要在每一次迭代中更新。同時，濾波器校正步驟的步長Δt則根據AIS 數據的發送頻率來設置。表1 列出了SCKF 初始參數的設置。表中：I4×4，I6×6分別為維度為4 和6 的單位矩陣； σx， σy分別為測量噪聲在X，Y軸方向上的位置方差。

表1 實驗初始參數設置Table 1 Setting of experimental initialization parameters

4.2 實驗與分析

在實驗過程中，將蒙特卡洛仿真次數設置為150 次，船舶軌跡的起始點設置為二維平面坐標系的原點 (0,0)。隨著航向、航向率和航速的變化，船舶可以產生不同類型的軌跡。本文將利用不同類型的軌跡來對比分析不同運動模型的適應場景，并驗證本文所提算法在船舶復雜運動場景下的性能。所采用AIS 數據的信息每10 s 更新一次。

AIS 數據存在航向信息和航速信息，不同的航向、航速變化情況對應不同的船舶運動狀態。圖4 展示了3 種單一運動狀態的船舶軌跡，通過這些軌跡，可以驗證并分析CVM，CSM 和CTM這些模型的性能及其使用場景。圖中，藍線表示船舶航行的原始軌跡，紅色的點表示船舶航行過程中的測量值，這可以通過各種傳感器獲得。測量值與原始軌跡的值之間存在一定的偏差。k時刻的測量值對應于AIS 數據中第k個點的位置信息，其需要參與本文算法的迭代運算，對SCKF 預測過程中狀態向量的預測結果進行校正，然后得到SCKF 算法的估計值 ()。原始軌跡在k時刻的值對應于式（24）中的 ()，真實值不參與本文算法的迭代運算，而是在實驗中結合SCKF算法的估計值 ()對算法進行性能分析。在圖4(a)展示的軌跡1 中，船舶的航向發生了變化，航速保持不變，船舶進行轉向勻速運動。在圖4(b)展示的軌跡2 中，船舶的航向和航速均保持不變，船舶進行直線勻速運動。圖4(c)所展示的軌跡3可以描述為船舶進行直線變速運動，其航向保持不變，航速發生變化。

圖4 3 種單一運動狀態的船舶軌跡和測量值Fig. 4 Trajectories and measurement values of ship with three single states of motion

圖5 展示的是基于CVM，CSM 和CTM 模型的KF 算法對圖4 中3 種軌跡跟蹤結果中位置的均方根誤差。觀察圖5（a）可以發現，對于航向變化、航速不變的船舶軌跡，基于CTM 的算法在整個跟蹤過程中誤差最小，基于CVM 的算法誤差始終比較大，而基于CSM 的算法性能僅次于基于CTM 算法的性能。觀察圖5（b）可以發現，對于航向、航速均不變的船舶軌跡，基于CVM 的算法誤差最小，基于CTM 的算法誤差最大，基于CSM 的算法誤差介于二者之間。觀察圖5（c）可以發現，對于航向不變、航速變化的船舶軌跡，基于CSM 的算法性能最好，基于CTM和CVM 的算法誤差較大，并且誤差波動的范圍也較大。綜合分析圖5，可以得出以下結論：

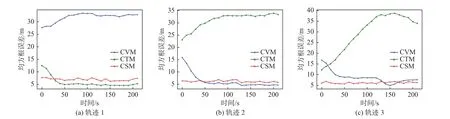
圖5 3 種單一運動狀態下圖4 跟蹤軌跡的位置信息均方根誤差Fig. 5 RMSEs of position data with three single states of motion in the trajectories shown in Fig. 4

1） CTM 模型對于航向變化的船舶運動的跟蹤能力更強，其不適用于船舶的直線運動。

2） CVM 模型對于船舶直線運動的跟蹤能力較強，最適合航向、航速均不變化的船舶運動，不適用于航向變化的船舶運動。

3） CSM 模型在對3 種軌跡跟蹤過程中均有比較不錯的表現，最適用于航速發生變化的船舶運動。

圖4 和圖5 分析了3 種單一船舶運動狀態下的場景，但在實際情況下，船舶的運動狀態會隨著航向和航速的變化而變化。圖6（a）所示為考慮船舶航向變化的場景。在航向發生變化后，船舶會由直線勻速運動變換為轉向勻速運動，當航向再次保持不變時，船舶又由轉向勻速運動變換為直線勻速運動。圖6（b）展示的是CVM，CTM單一運動模型和組合模型1 對船舶軌跡跟蹤的整個過程中位置信息的均方根誤差。表2 統計了組合模型1 與單一運動模型在船舶不同運動狀態下對應時間段內局部位置的平均均方根誤差，其中組合模型1 是通過IMM 框架將CVM 與CTM 兩種運動模型進行的交互融合。由圖6 和表2 可以觀察到，基于CTM 模型的算法在軌跡4 的直線段誤差較大，基于CVM 模型的算法在軌跡4 的曲線段誤差較大，基于組合模型1 的算法因融合了CVM 與CTM 這兩種模型的優勢，在不同時間段內可切換到跟蹤能力較強的模型，使得能夠將組合模型的誤差穩定在較低范圍內。因此，對于存在航向變化的船舶軌跡，適合采用組合模型1 來進行船舶軌跡跟蹤。

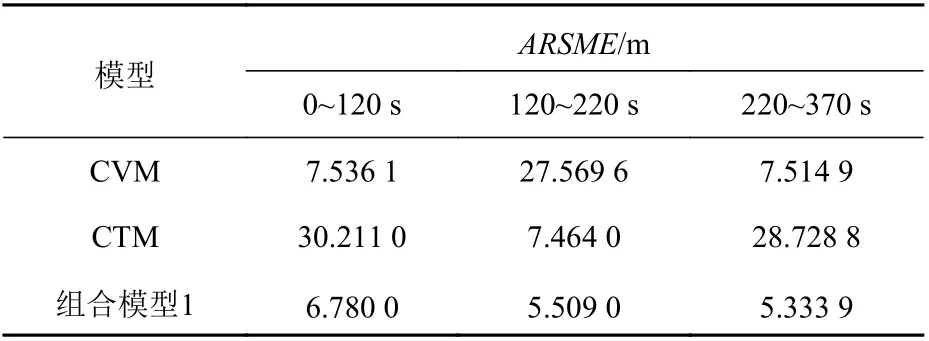
表2 組合模型1 和單一模型在不同時間段跟蹤軌跡4 的位置信息平均均方根誤差Table 2 ARMSEs of local position data at different time periods in Trajectory 4 using Combined Model 1 and single motion model

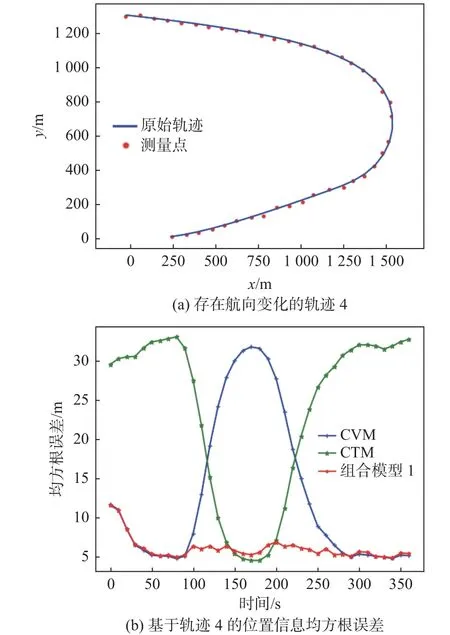
圖6 組合模型1 和單一模型跟蹤軌跡4 位置信息均方根誤差Fig. 6 RSMEs of position data in Trajectory 4 using Combined Model 1 and single motion model

在船舶運動過程中，是通過操舵來改變船舶航向，不同的舵角對應的船舶轉向率也不同，因此在實際的船舶運動過程中，存在具有不同轉向率的轉向運動場景。軌跡4 描述的是只具有一種轉向率的場景，而圖7（a）中的軌跡5 描述的則是船舶轉向率發生變化的運動場景。CTM 模型采用的是固定的轉向率，當船舶實際的轉向率與CTM 模型中設置的轉向率偏差較大時，其擬合效果會較差，從而影響到組合模型1 在轉向運動階段的跟蹤性能。由于實驗中采用的AIS 數據中缺少轉向率的信息，本文將通過已知的AIS 軌跡點的航向信息來估計轉向率，形成改進的CTM模型，然后再將改進的CTM 與CVM 模型進行交互融合進而形成組合模型2。

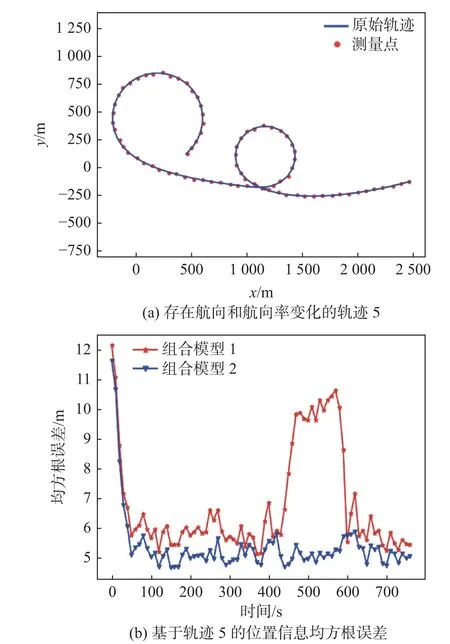
圖7 組合模型1 和2 跟蹤軌跡5 的位置信息均方根誤差Fig. 7 RSMEs of position data in Trajectory 5 using Combined Model 1 and 2

如圖7（b）所示，在2 次轉向運動階段，尤其是在第2 次轉向運動階段，基于組合模型1 的算法誤差較大，出現了跟蹤結果局部發散的現象。基于組合模型2 的算法在整個軌跡跟蹤過程中誤差均較小，且誤差的波動范圍也較小。表3 給出了組合模型1 和2 在軌跡5 中不同時間段的局部位置平均均方根誤差。從中可以看出，在第1 次轉向運動階段，采用組合模型2 的算法其誤差與采用組合模型1 算法的誤差相差不大；在第2 次轉向運動階段，組合模型1 中CTM 模型設置的轉向率與實際的轉向率偏差較大，導致其跟蹤誤差出現了大幅度的變化；組合模型2 因融合了改進的CTM 模型，其跟蹤誤差保持在較穩定的范圍內，因此對于存在航向變化及航向率變化的船舶運動，組合模型2 的適應能力較好。

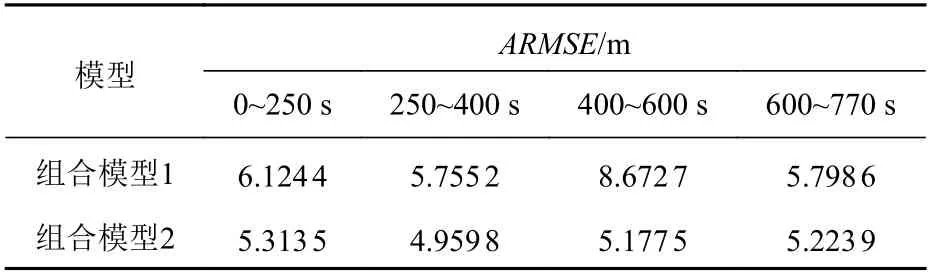
表3 組合模型1 和2 在不同時間段跟蹤軌跡5 的位置信息平均均方根誤差Table 3 ARMSEs of position data at different time periods in Trajectory 5 using Combined Model 1 and 2

在實際的船舶運動過程中，除航向的變化外，還需要考慮航速變化的場景。圖8（a）所示的軌跡6 描述的是航向變化、轉向率變化以及航速變化時的船舶運動，圖8（b）展示的則是軌跡6 中航速的變化情況。考慮到基于CSM 模型的算法適用于航速發生變化的船舶運動，本文將通過IMM框架實現CVM，CSM 和改進的CTM 模型進行交互融合而形成組合模型3。

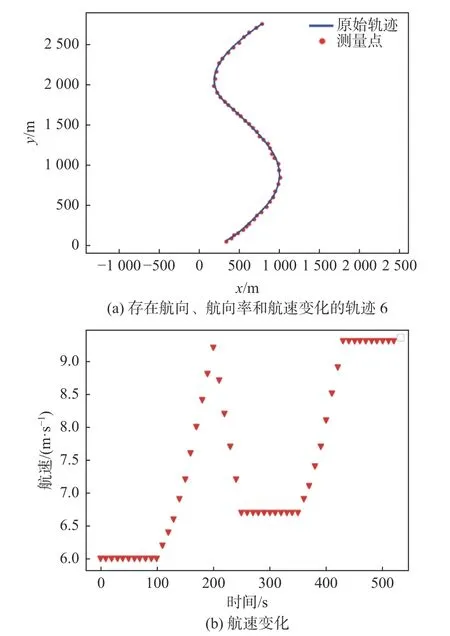
圖8 軌跡6 及其航速的變化Fig. 8 Trajectory 6 and its velocity variation

圖9 所示為對軌跡6 進行跟蹤得到的位置信息均方根誤差。一方面，采用組合模型1 分別搭配EKF 算法和SCKF 算法，并對這2 種KF 算法進行了對比分析。在整個跟蹤過程中，組合模型1對軌跡6 相關船舶運動狀態的描述不夠準確和全面，導致采用該模型的2 種KF 算法都出現了誤差明顯增大的現象，這種現象被稱之為局部發散。由圖可以明顯觀察到，采用SCKF 算法時，誤差變化幅度遠小于EKF 算法 ，SCKF 算法對局部發散現象的抑制能力要優于EKF 算法。由表4 可知，SCKF 算法的平均均方根誤差為10.975 5 m，EKF 算法的為15.693 5 m，精度提高了30.06%。總體而言，在軌跡跟蹤過程中，SCKF 算法的穩定性要優于EKF 算法。

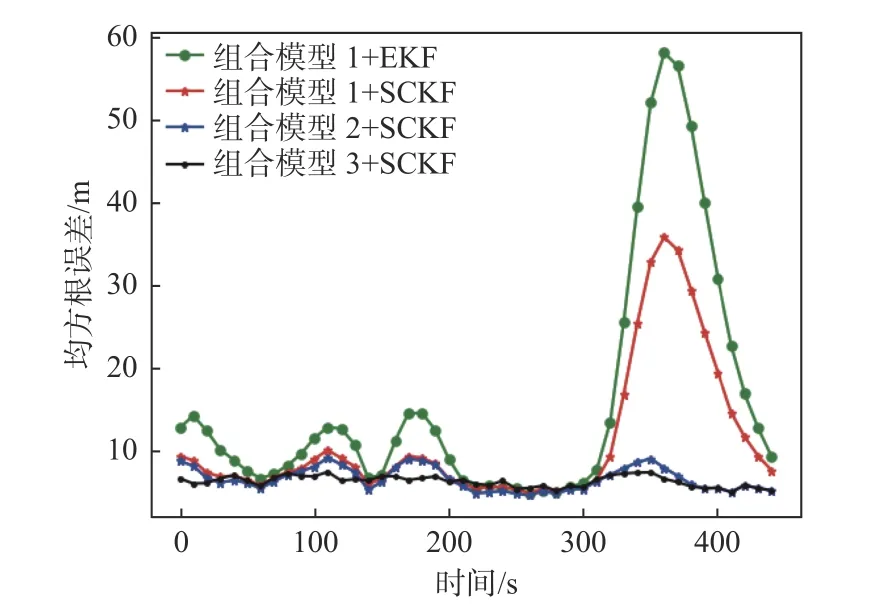
圖9 3 種組合模型搭配卡爾曼算法跟蹤軌跡6 的位置信息均方根誤差Fig. 9 RMSEs of position data in Trajectory 6 using three combined models with Kalman filtering algorithm

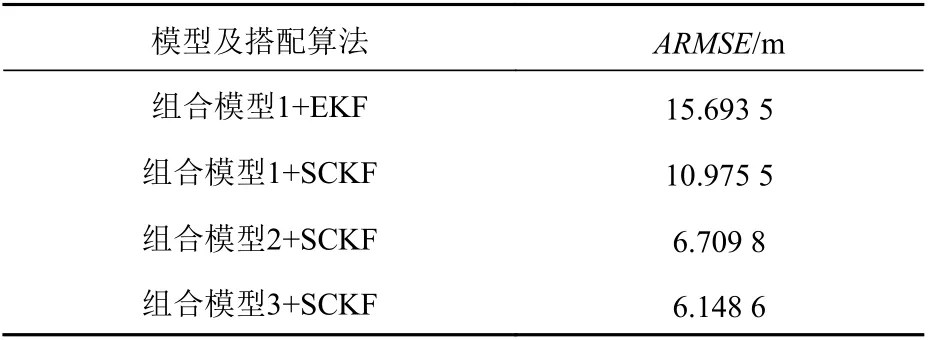
表4 3 種組合模型搭配卡爾曼濾波算法跟蹤軌跡6 的位置信息平均均方根誤差Table 4 ARMSEs of position data in Trajectory 6 using three combined models with Kalman filtering algorithm

另一方面，分別對比分析了組合模型1，2，3搭配SCKF 算法時對軌跡6的跟蹤過程中位置的均方根誤差。結果顯示，采用組合模型1 搭配SCKF 算法在航速發生改變的時間段存在小幅度的誤差增大現象，在轉向率變化的時間段誤差大幅度增大，其對船舶復雜運動的適應能力較弱；采用組合模型2 搭配SCKF的算法在轉向率變化的時間段擁有比基于組合模型1 的算法有更好的跟蹤能力，但在航速變化的時間段仍存在小幅度的誤差增大現象；采用組合模型3 搭配SCKF 的算法的誤差也受到了航速變化的影響，但誤差波動范圍明顯小于前2 種算法，整個軌跡位置的誤差曲線更加平滑。

由表4 中數據可以知道，在整個軌跡跟蹤過程中，采用組合模型2 搭配SCKF 算法其位置的平均均方根誤差為6.709 8 m，采用組合模型3 搭配SCKF 算法的位置平均均方根誤差為6.148 6 m，說明在跟蹤精度上采用這2 種算法其性能相差不大，兩者在性能上的差異主要體現在穩定性方面。結合圖9 和表4 的實驗結果可以得出結論：組合模型3 搭配SCKF 的算法對于存在航速變化的復雜船舶運動的適應能力比較強，其能將軌跡跟蹤誤差穩定在較小的區間范圍內。

從濾波器的角度來講，本文引入的SCKF 算法在跟蹤軌跡方面其誤差變化幅度比EKF 算法的小；從運動模型的角度來講，組合模型3 搭配SCKF 算法對存在航向、航向率和航速變化的船舶運動的適應能力最強，此種算法軌跡跟蹤的位置信息均方根誤差變化曲線最平滑，且相比組合模型1 結合EKF 算法其平均均方根誤差減小了60.80%。

前面的實驗涉及了3 種組合模型，圖10 和表5分別展示了這3 種組合模型搭配SCKF 算法跟蹤6 類軌跡過程中的位置信息均方根誤差以及平均均方根誤差。其中，軌跡1，2，3屬于狀態變化比較單一的軌跡，軌跡4，5，6 屬于狀態變化比較復雜的軌跡。從中可以觀察到，在所有軌跡的實驗中，組合模型1 的性能是最差的，不建議采用；在軌跡1，2，3 的跟蹤結果中，組合模型3 的效果明顯優于組合模型2；在軌跡4，5 的跟蹤結果中，組合模型3 的誤差最小，與組合模型2的誤差非常接近；軌跡6 涉及到航速的變化，在其跟蹤結果中，組合模型3 的誤差明顯低于組合模型2。不過，因組合模型3 包含3 種運動模型，相比組合模型2 的2 種運動模型，需要多設置一個濾波器，故計算量更大。結合以上分析，得到結論如下：

表5 3 種組合模型搭配SCKF 算法跟蹤6 條軌跡的位置信息平均均方根誤差Table 5 ARMSEs of position data in the six trajectories using three combined models with SCKF algorithm

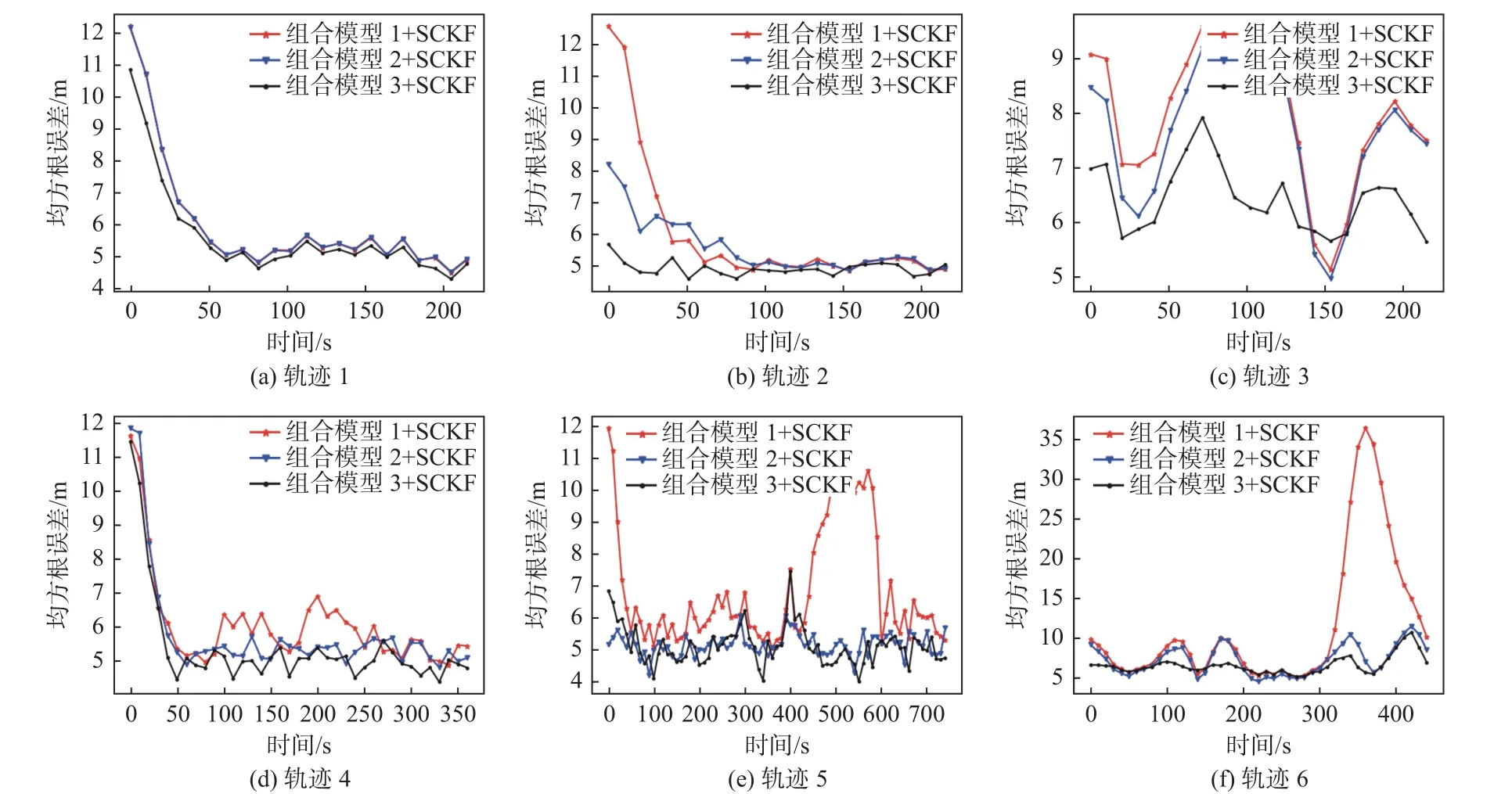
圖10 3 種組合模型搭配SCKF 算法跟蹤6 條軌跡的位置信息均方根誤差Fig. 10 RMSEs of position data in the six trajectories using three combined models with SCKF algorithm

1） 在所有場景下，組合模型3 的性能都是最好的，但計算量也是最大的；

2） 對于狀態變化比較簡單的軌跡，建議采用組合模型3；

3） 對于狀態變化比較復雜的軌跡，如果不存在航速的變化，在缺乏計算資源的情況下，建議采用組合模型2，其他情況下采用組合模型3 效果更好。

圖11 所示為在船舶軌跡6 的軌跡跟蹤實驗中，組合模型2 和3 的基礎模型的概率隨船舶運動變化的時序圖。圖中，各條曲線分別顯示了其對應基礎運動模型濾波后的模型概率，代表了當前時間步長模型的依賴程度。曲線的概率越高，所對應的模型越有可能在當前時間步長用于軌跡跟蹤。軌跡6 包含有直線運動、轉向運動和變速運動，在圖11 中，組合模型2 的概率曲線的變化情況比較混亂，無法準確識別軌跡6 運動狀態的變化；相比而言，組合模型3 的概率曲線的變化更具規律性，能夠描述出軌跡6 運動狀態的變化。然而，模型的切換存在較小的滯后，這是因為濾波器不是依靠精確的船舶運動模型進行迭代計算，而是通過迭代計算測量值與估計值間的差值，逐漸切換到該差值最小時所對應的運動模型，從而完成模型的過渡。這種轉換過程需要一些時間，因為測量值與估計值間的差值不會顯著或是立即改變。

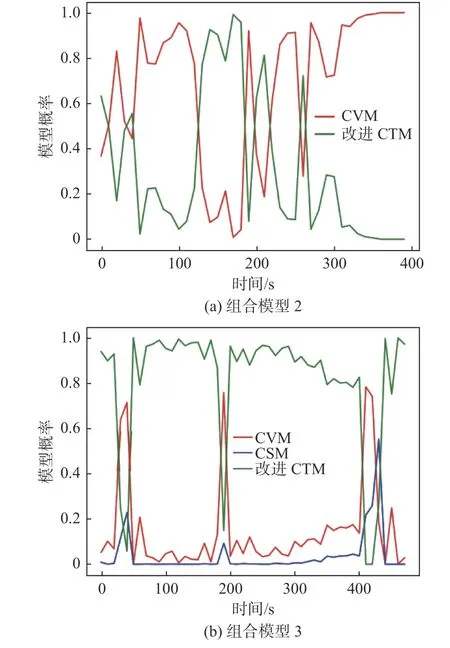
圖11 組合模型2 和3 在軌跡6 中的模型概率時序圖Fig. 11 Time-series of model probabilities for Combined Model 2 and 3 in Trajectory 6

5 結 語

AIS 是海上交通普遍使用的一種系統，針對AIS 數據中存在虛假信息以及不連續性的問題，本文提出了一種IMM-SCKF 算法來對船舶軌跡進行跟蹤。通過引入SCKF 算法代替EKF 算法來執行對AIS 數據的軌跡跟蹤，避免了EKF 算法容易出現局部發散的現象，提高了濾波器的數值穩定性。采用IMM 框架將多個模型進行融合并進行自適應轉換，表征了船舶在不同時刻的運動狀態。首先，對參與模型融合的CTM 運動模型進行改進，用已知AIS 軌跡點的航向信息來估計轉向率，并替代CTM 的固定轉向率，使得組合后的模型能夠更好地表征船舶航向的變化。隨后，通過對比實驗，驗證了基于CVM，CSM 和改進CTM 的組合模型在各種類型船舶軌跡的跟蹤實驗中都具有最小的誤差和誤差波動幅度，適合大多數情況下的船舶軌跡跟蹤。然而，基于CVM，CSM 和改進CTM 的組合模型計算量比較大，當計算資源緊張且船舶存在航向和航向率變化特征時，可以考慮采用CVM 和改進CTM 的組合模型進行軌跡跟蹤。

總體而言，本文提出的IMM-SCKF 算法能對船舶在不同時刻的運動狀態進行較為全面和準確的描述，其在實際的軌跡跟蹤過程中，在跟蹤精度和穩定性兩個方面均有著比較理想的效果，能有效提高AIS 的服務質量，為船舶軌跡的預測和船舶導航提供有力的支撐。然而在實驗過程中，IMM 框架下模型的實際切換過程相比理想的切換過程存在一定的滯后，這在一定程度上影響了IMM-SCKF 算法在運動狀態變換時軌跡跟蹤的精度。