優化形態學濾波在高速列車軸承故障診斷中的應用*
王茂輝,王 濤,陳 嬌,夏 偉,楊 浩,吳 震
(1 重慶工商職業學院 智能制造與汽車學院,重慶 401520;2 西南交通大學 牽引動力國家重點實驗室,成都 610031)
軸箱軸承作為高速列車的重要組成部分,越來越多的學者致力于研究用不同方法獲取軸承運行狀態。故障診斷過程包括3 部分:故障背景信息搜集、故障特征提取以及故障部位或故障狀態確認,其中后2 部分較為關鍵[1]。
軸箱軸承的故障特征極其微弱,常常淹沒在其他振動信號及無關噪聲中。如何從高噪聲背景下提取軸承相關特征是關鍵。目前基于振動信號的軸承故障診斷方法有很多,常用的方法包括傅里 葉 變 換(Fourier Transform,FT)[2]、小 波 變 換(Wavelet Transform,WT)[3]、經驗模態分解(Empirical Mode Decomposition,EMD)[4]等。
傅里葉變換通常轉換到頻域尋找軸承故障特征,根據頻域幅值及凸顯程度來判定故障位置和故障程度。然而,在實際采集到的振動信號中,除了軸承故障相關信號外,還包含了大量無關噪聲的干擾,提取的有效信息有限。小波變換具有多分辨特性,適合用于處理非平穩信號,但是小波基的選取沒有明確的規定,一般基于先驗知識選取,難以自適應完成。經驗模態分解相比小波變換具有完全自適應性,但是分解結果模態混疊現象嚴重,缺乏充足的理論依據。
形態學濾波最初由數學形態學理論演化而來,之后Serra 等[5-9]從數學理論框架等多方面對形態學濾波做了深入的研究。目前,數學形態學濾波(Mathematical Filter,MF)在機械設備故障診斷領域中做了大量應用。章立軍[10]對結構元素選取方法做了一些說明;唐貴基和胡愛軍等[11]研究了開閉、閉開等組合形態算子對于濾波降噪、提高測試信號信噪比的有效性。但是,作者認為目前針對旋轉件故障信息提取過于依賴先驗知識,結構元素相關參數(長度L和高度h)未結合信號特征做自適應選取,對軸承早期故障信息提取效果有限。
至此,文中提出了結合布谷鳥尋優算法與形態學濾波算法綜合運用到高速列車軸箱軸承故障檢測中。對于確定的形態學濾波運算,用布谷鳥算法對結構元素參數進行優化,選用峭度系數(Kurtosis)為適應值函數,依據峭度最大值時獲取最佳結構元素。
1 形態學濾波基本原理
形態學濾波算法就是設計一個類似于濾波窗的結構元素,結構元素在信號上平移篩選與結構元素相適應的特征,可以實現提取特征,去除無關噪聲的目的[12]。
1.1 基本運算
形態學濾波的基本運算包括[14]:擴張、腐蝕、開運算和閉運算。定義f(n)為原始一維信號,定義域為[0,N-1];g(m)為結構元素,定義域為[0,M-1]。利用g(m)對f(n)完成多種運算,運算公式為式(1)~式(4):
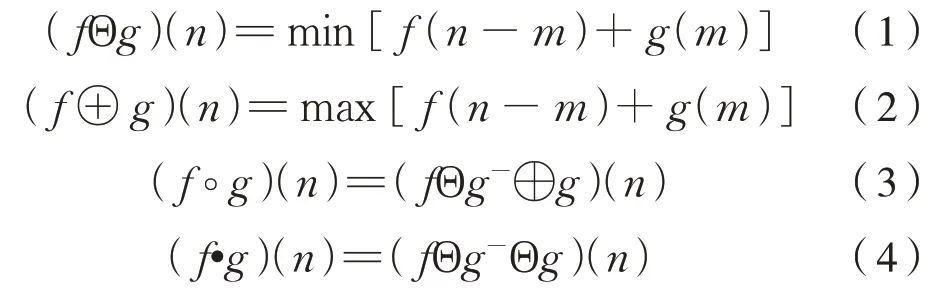
式中:g-(m)=g(-m);⊕為膨脹運算;Θ 為腐蝕運算;°為開運算;·為閉合運算。
1.2 結構元素
當前常用的結構元素(Structural Element,SE)形狀主要有三角形和直線形,如圖1 所示。
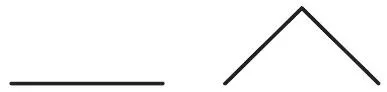
圖1 常見SE 形狀
此外,結構元素的長度和高度參數選取也至關重要,其矩陣構造方式見表1 和表2。當選擇尺度較小時,提取有效特征不充分,當尺度較大時,易丟失信號細節成分,因此,需要合理的選擇結構元素尺度[14]。

表1 直線形結構元素的矩陣結構

表2 三角形結構元素的矩陣結構
結構元素最大尺度為式(5):

式中:fs為采樣頻率;f0為故障特征頻率。
1.3 常用形態學濾波運算
在實際采集到的軸承故障信號中,通常包含正負2 個方向的沖擊,而單個基本運算只能提取單方向的故障特征,因此需要對4 種基本運算進行組合,構建出效果較好的形態學濾波運算[13]。目前最常用且效果較好的是形態學梯度濾波運算(Morphological Gradient,MG),其定義為式(6):
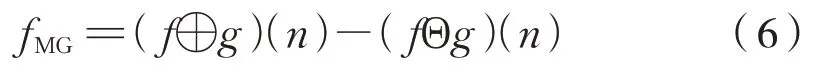
2 布谷鳥算法
2.1 巢寄生育雛
布谷鳥的繁衍“寄生”行為通常會選擇成活率較高的鳥巢。當寄生蛋在寄主鳥巢中被發現,布谷鳥就會把該鳥巢做標記,其后代在選擇鳥巢寄生時會避開這類鳥巢。經過多代更替,布谷鳥寄生巢數量和位置日趨穩定,其孵化下一代的數量也達到最大值[14]。
2.2 萊維飛行
L’evy 飛行[15](也稱萊維飛行)主要用于尋找最優搜索路徑。布谷鳥主要以短距離小步長飛行,因此可以將尋優步長設置較小,步長SP的發生概率l(SP)為式(7):
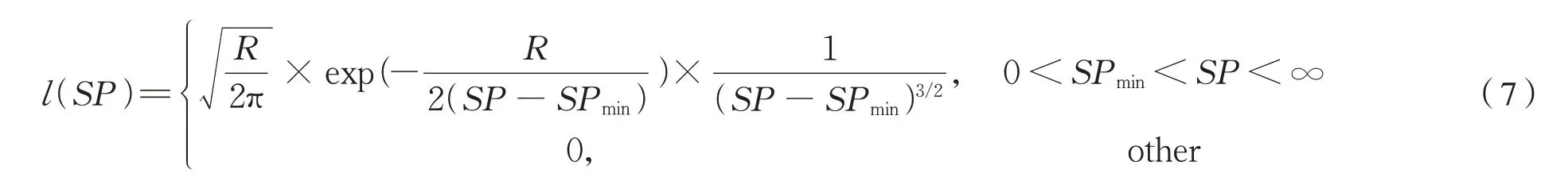
式中:R為模式控制參數;SPmin為最小步長。
3 評價指標
峭度指標(Kurtosis)[16]是信號歸一化的四階中心距,該指標對于信號中的沖擊成分較為敏感。一般情況下,當峭度值超過4 時,表明在該信號中可能存在較為明顯的沖擊特征。對于一維信號xi(i=1,2,……,N),其表達式為式(8):
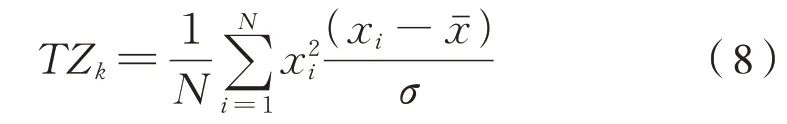
式中:為均值;σ為標準差。
4 CS-MF 算法
根據以上理論介紹,文中提出了基于布谷鳥尋優的改進形態學濾波算法,算法流程如圖2所示。
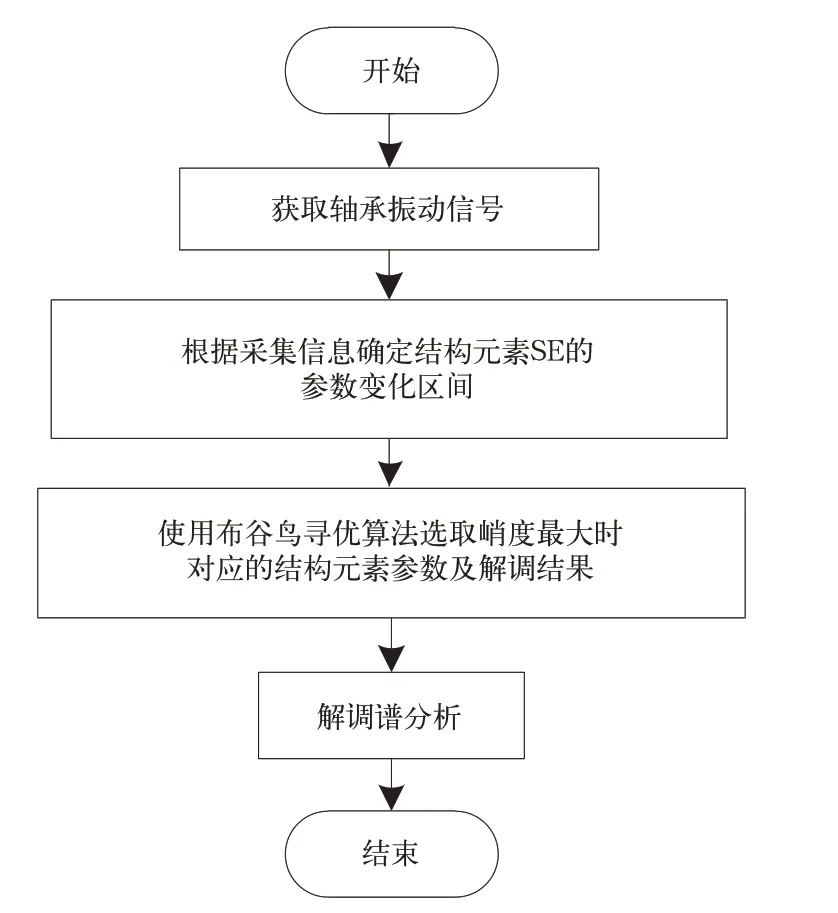
圖2 算法流程圖
其具體步驟如下:
(1)通過振動加速度傳感器獲取軸承振動信號f(t)。
(2)根據采樣頻率和故障特征頻率確定結構元素SE 的參數變化區間,文中設置高度h范圍為[1,20]。
(3)應用選定的MG 運算,由于不同尺度結構元素下可獲得不同解調結果,通過布谷鳥尋優算法根據峭度值最大原則自適應尋找最優解調結果。
(4)對最優解調結果做頻譜分析,觀察是否存在故障特征。
5 仿真驗證
為了驗證文中所提算法在強噪聲背景下依然有效,文中仿真軸承外圈故障信號,仿真信號為式(9):
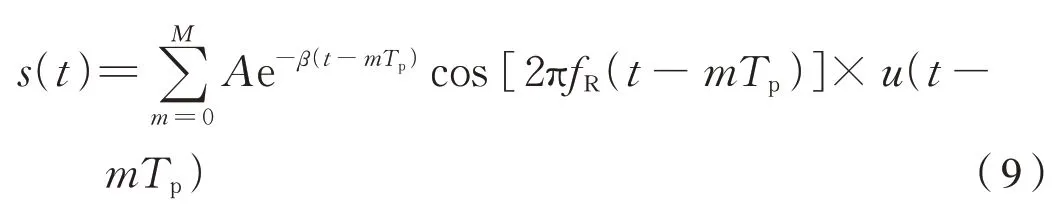
式中:A為沖擊信號的幅值,A=5;TP為沖擊信號重復周期;fR為共振頻率,fR=3 000 Hz;β為阻尼系數,β=1 200 N?s/m。設置外圈故障特征頻率為142.6 Hz。
仿真信號采樣頻率fs=10 000 Hz,信號長度為1 s。在仿真信號中添加SNR=-13 dB 的高斯白噪聲。仿真信號的時域波形如圖3 所示,頻譜和包絡解調譜如圖4 所示。
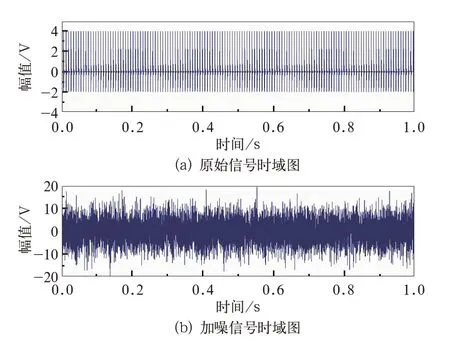
圖3 仿真信號時域
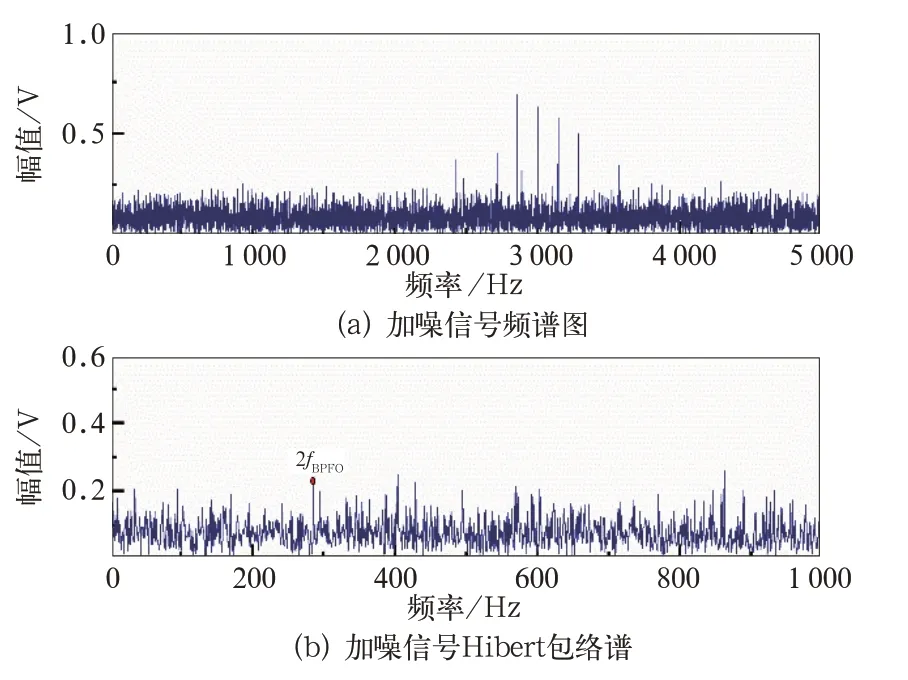
圖4 仿真信號頻譜和包絡譜
圖3(a)為未加噪聲的循環沖擊信號,圖3(b)為含噪信號時域圖,從圖中可以看出循環沖擊信號已完全被噪聲覆蓋,無法得到有效信息;仿真信號頻譜和包絡譜在圖4 中可見,圖4(a)含加噪信號的頻譜圖中可以看出共振頻帶集中在3 000 Hz附近。為了便于觀察,將包絡解調譜中顯示頻率范圍設置在0~1 000 Hz,由于噪聲干擾,僅能看到2 倍故障特征頻率,Hilbert 包絡解調很難獲取有效信息,無法對軸承狀態進行判斷。
將文中所提的優化形態學濾波算法運用到本次仿真信號中,對所獲取的解調結果做傅里葉變換,效果如圖5 所示。最優解調結果對應的結構元素為直線形,尺度為5,高度為1,對應的峭度值為13.365。
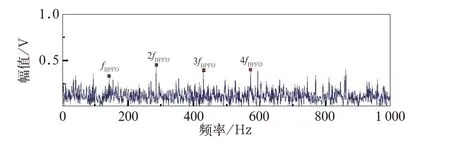
圖5 優化形態學濾波解調譜
為了更全面驗證文中所提方法的有效性,使用Teager 能量算子解調對仿真信號進行分析,結果如圖6 所示。
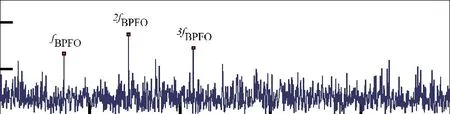
圖6 Teager 能量算子解調譜
基于以上3 種解調方法效果對比可知,文中所提方法可以較為明顯觀察到1~4 倍故障特征頻率,而Teager 能量算子解調僅能看到1~3 倍故障特征頻率,Hilbert 包絡解調僅能看到2 倍故障特征頻率。因此該方法相對于常用解調算法能夠較為充分地提取信號中的故障特征,提高故障診斷可靠性。
6 試驗驗證
為了驗證文中所提算法對于臺架實測數據依然有效,本章節使用高速列車整車試驗臺的振動數據對算法進行驗證。
某CRH3 型高速列車的整車試驗臺如圖7 所示,故障試驗完成了高速動車組軸箱軸承的外圈劃痕故障臺架試驗,監測部位局部放大圖如圖8 所示,通過振動加速度傳感器采集試驗臺運行過程中軸箱振動加速度信號,其采樣頻率為10 kHz,安裝位置在圖中標注。軸箱內使用的軸承為雙列圓錐滾子軸承,軸承相關參數見表3,其結構如圖9所示。

圖7 某CRH3 型高速列車整車試驗臺

圖8 被監測部位局部放大圖

表3 NSK 軸承參數
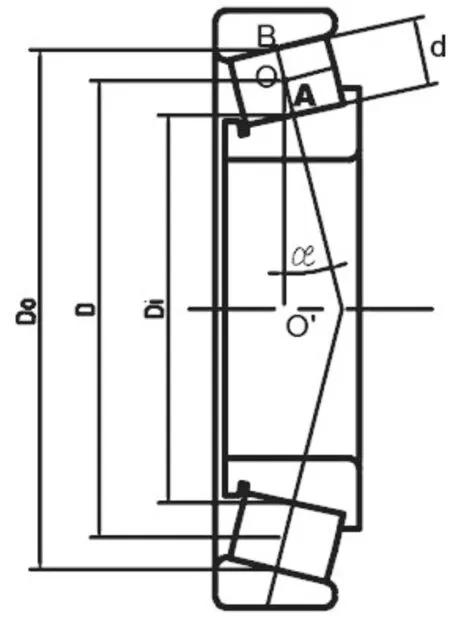
圖9 圓錐滾子軸承結構圖
軸承外圈故障特征頻率計算為式(10):
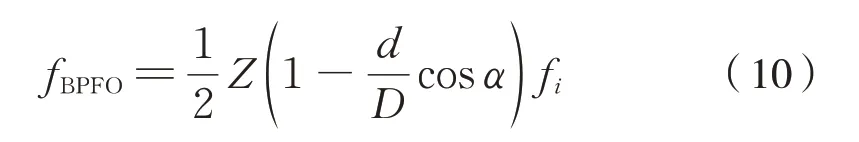
取1 s 的振動信號進行分析,在勻速工況下,根據上式計算可得對應的特征頻率是256 Hz。振動加速度信號如圖10 所示。
圖10(a)為軸箱振動加速度信號的時域波形,圖10(b)為頻譜圖,可以看出受無關噪聲影響,從信號中無法觀測到任何循環沖擊成分,且頻譜中存在50 Hz 工頻干擾,幅值達到2.34 m/s2,頻譜分布無規律。對振動信號進行包絡譜分析,其結果如圖10(c)所示,顯然Hilbert 包絡譜中無法識別與外圈故障特征頻率相關的頻率成分,且存在無關干擾。
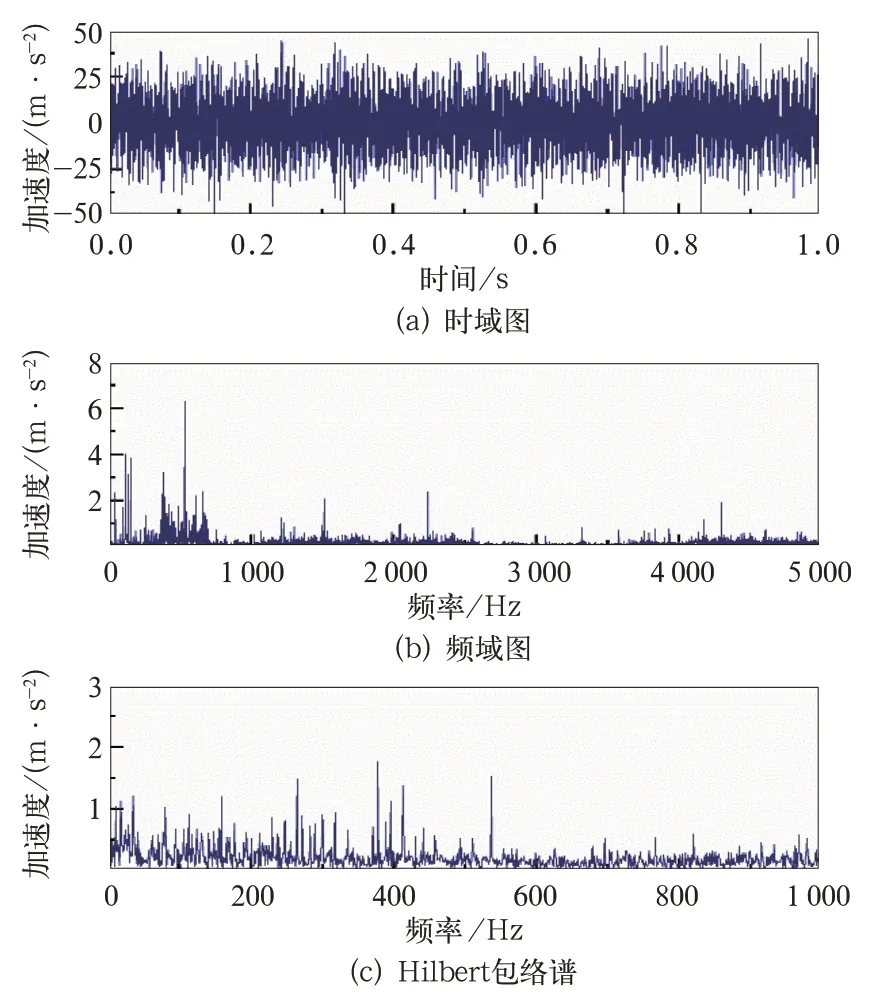
圖10 軸箱振動加速度信號
使用基于布谷鳥尋優的形態學濾波算法對信號進行處理,經過不斷的迭代尋優,根據峭度值最大原則,得到的最優結構元素長度為5,高度為2,三角形結構,其對應的解調譜如圖11 所示。

圖11 優化形態學濾波解調譜
運用Teager 能量算子解調結果如圖12 所示,通過比較可知,優化形態學濾波算法和Teager 能量算子解調都能提取較多的故障特征,但在抑制無關噪聲方面,Teager 能量算子解調效果稍顯不足,而優化形態學濾波解調譜的故障特征較為凸顯,大大提高了故障診斷的可靠性。
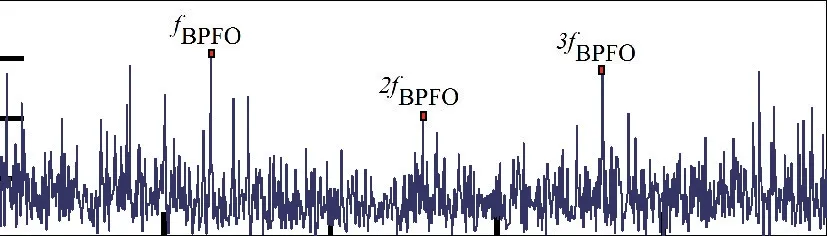
圖12 Teager 能量算子解調譜
綜上所述,該方法不僅可以對仿真信號中的循環沖擊進行識別,也可以對臺架實測試驗數據中的循環沖擊進行有效識別,有效抑制無關噪聲干擾。
7 結束語
文中將布谷鳥尋優算法和形態學濾波算法相結合,提出了一種新的高速列車軸箱軸承故障診斷方法。
(1)基于峭度值指標最大原則作為布谷鳥尋優依據,解調結果中故障特征更為凸顯。
(2)布谷鳥尋優算法具有運算速度快、準確度高等優點,可以自適應尋找最佳結構元素參數(高度h和長度L)。
(3)通過仿真試驗以及臺架試驗驗證了該方法的有效性,可以有效的提取軸承的故障特征,為高速列車軸箱軸承故障檢測提供了一種新的方法。

