基于PSO優化BP神經網絡的多傳感器數據融合

朱菊香， 谷 衛， 羅丹悅， 潘 斐， 張趙良

(1. 無錫學院軌道交通學院，江蘇 無錫 214105; 2. 南京信息工程大學自動化學院，江蘇 南京 210000)

0 引 言

隨著我國經濟的快速發展，人們越來越重視室內環境質量。傳統的室內環境質量監測依然局限于單一傳感器采集室內環境參數，而傳感器易受環境因素以及傳感器自身品質的影響，導致測量精度低、可靠性差[1]。為了突破單一傳感器監測環境的簡單性和局限性以及避免單一傳感器信息盲區的問題，提高檢測精度，本設計通過使用多傳感器數據融合技術對目標進行檢測并對采集到的環境數據進行融合[2]。

張邦成等提出基于改進BP神經網絡算法，融合精度較高，但是算法運行時間較長且抗干擾能力較差[3]；張珂在異步數據融合算法中雖然可以在一定程度上有效解決跟蹤性能，但是融合精度較低[4]；Pau Ferrer-Cid通過貝葉斯算法對數據進行了預處理，減少了數據的波動，并且對加權平均算法進行了優化，縮短了算法的運行時間，但是這種方法在運算時占用的存儲空間較大[5]；郭連進提出了自適應加權和模糊集合融合算法，抗干擾能力差，融合精度較低[6]。

針對上述問題，本文提出了基于粒子群（particle swarm optimization，PSO）優化BP神經網絡的多傳感器數據融合算法，提高測量數據的可靠性和融合精度。首先使用防脈沖干擾平均濾波算法對測量數據進行預處理，剔除傳感器測量數據中的異常值提高抗干擾能力。然后，結合卡爾曼濾波算法和PSO優化BP神經網絡算法對預處理后的數據進行融合，得到最佳融合數據。最后，用實驗數據來驗證該融合算法的有效性。

1 數據融合算法

數據融合，又稱為信息融合或多傳感器數據融合，是將各個地方的傳感器收集的信號有機地結合起來，使物體得到更清晰的識別[7]。多傳感器數據融合可以提高信息的可靠性和目標的可探測性；可以獲得單一傳感器所不能獲得的全面、準確信息；可以通過整合各種傳感器采集的多個數據而不是單個數據來獲取更多信息[8]。這是協同效應的結果，即多傳感器的綜合效應，使系統的可靠性得到增強。多傳感器數據融合是解決單一傳感器測量數據精度低、穩定性差的關鍵技術。從不同時空的多源數據中，消除冗余信息，減少數據傳輸，從而達到提高信息采集的精度、增強系統穩定性的目的[9]。

根據室內環境監測的特點，在室內的各個房間的不同位置布置傳感器，系統需要多種傳感器采集多種環境參數，即使對同一環境參數，也需要多個同類傳感器布置在多個位置進行多點采集。采集同一環境參數的傳感器為同質傳感器，采集不同環境參數的傳感器為異質傳感器，該文采用同類傳感器數據級融合和異類傳感器決策級融合相結合的融合方式[10]。該文融合算法模型如圖1所示。

圖1 融合算法模型

2 同質傳感器融合算法

在實際檢測系統中，檢測空間的大小直接導致了采集環境數據量的變化，檢測環境和傳感器的性能參數也會影響采集數據的有效性。鑒于上述分析，本文采用了防脈沖干擾平均濾波算法和卡爾曼濾波融合算法相結合的方法構成一級數據融合。該方法將測量值放入融合算法模型中，利用一定的規則獲得更科學、全面的環境信息。

2.1 數據預處理

本文將采集室內五個環境參數，包括溫度、濕度、甲醛、PM2.5以及揮發性有機化合物（volatile organic compounds, VOC）。由于傳感器易受到偶然因素影響，引起一定脈沖干擾，故本文在環境參數采集終端植入相應的限幅濾波算法，該算法能有效克服因偶然因素引起的脈沖干擾。算法的計算過程為：對于每個采樣值，判斷采樣值與上次采樣值之間的絕對值差，如果小于或等于范圍值，則采樣值有效；如果大于或等于范圍值，則使用上次采樣值。但該算法的平滑度較差，不能抑制周期性干擾。因此，在環境參數采集終端中使用的限幅濾波算法，在此基礎上添加中位值平均濾波算法簡稱防脈沖干擾平均濾波算法，該算法結合中位值濾波算法和算術平均濾波算法，可以克服上述兩種算法的不足。該算法的原理是：對于連續的個數據進行排列，刪除最大和最小的兩個數據，計算個數據的算術平均值。采集室內甲醛含量，發現甲醛值會跳變。防脈沖干擾平均濾波算法的應用可以很好地過濾除這些干擾(限幅閾值為0.05 mg/m3)，如圖2所示。

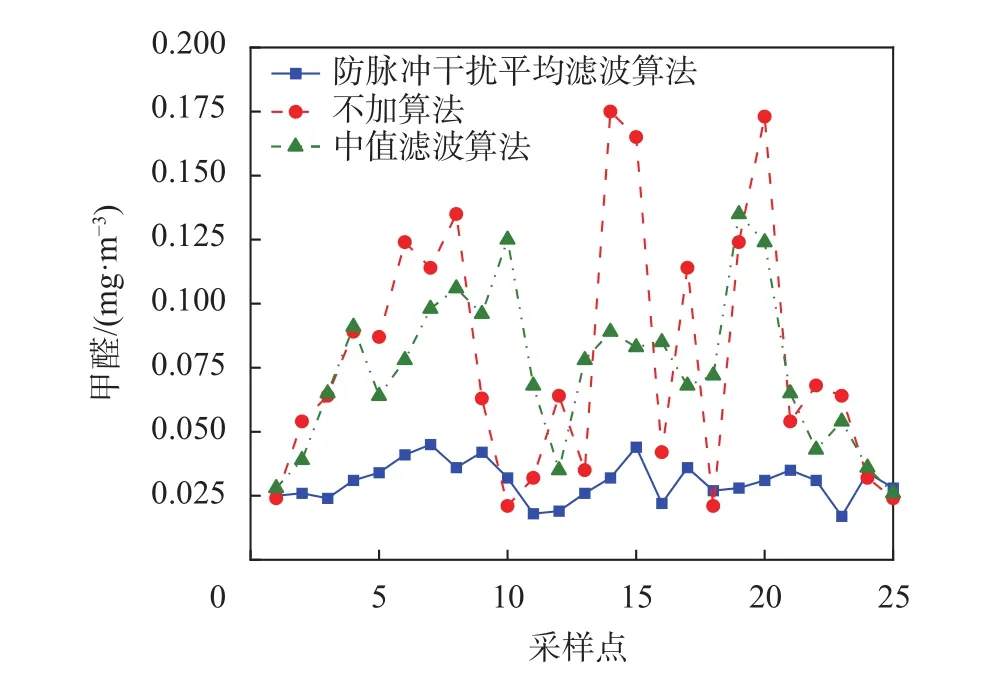
圖2 算法對比圖

2.2 卡爾曼濾波融合算法

預處理后的數據仍然混有測量噪聲和各種干擾信號。為了有效控制噪聲對數據融合的影響，采用卡爾曼濾波算法對預處理后的環境數據進行優化，使之更接近真實值，成為最優數據集。

卡爾曼濾波是以最小均方誤差為準則的遞推無偏估計算法，該算法容錯性強，主要用于融合底層實時動態多傳感器冗余數據。該方法利用測量模型的統計特性，迭代確定統計意義上的最佳融合和數據估計[11]。降低了同類傳感器數據采集過程中由于傳感器自身干擾和部件老化造成的隨機測量誤差以及傳感器受到環境（溫度、濕度、氣壓、風速、光照）等外部因素對傳感器的造成的噪聲污染問題，卡爾曼濾波可以充分抑制噪聲對真實數據的干擾，為二級數據融合提供統計上準確有效的數據。因此，第一級融合將采用卡爾曼濾波算法。卡爾曼濾波算法的流程圖如圖3所示。

圖3 Kalman算法流程圖

卡爾曼濾波算法主要步驟如下：

5）為了使卡爾曼濾波算法可以不斷運行迭代下去，還需要每次迭代過程中更新當前時刻下的協方差。

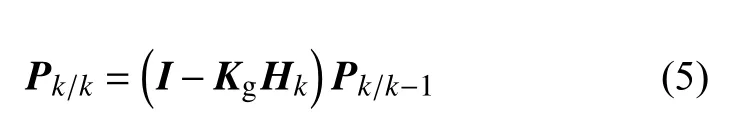
根據上述方程式的描述，可以將卡爾曼濾波分為預測過程和修正過程。預測過程是根據前一時刻的估計值來預測當前狀態；修正過程是結合當前時刻的觀測值和估計值，得到更接近真實值的最優估計值。該算法按照上述過程繼續迭代，只需要保存前一時刻的計算參數，不需要占用大量的儲存空間，提高算法運行的效率。為了更好地體現卡爾曼濾波的性能，用Matlab仿真溫度在24 ℃情況下的輸出結果，如圖4所示。

圖4 Matlab仿真24 ℃示意圖

從圖中可以看出，傳感器的測量值與真實值24 ℃相比誤差較大，導致誤差較大的主要原因是傳感器受自身品質影響以及環境因素的干擾，測量偏差較大，而卡爾曼濾波算法可以很好地抑制噪聲和環境干擾，使得測量值更接近真實值。

為了更好地顯示出卡爾曼濾波算法的優越性，通過對采集的36組環境數據分別進行卡爾曼濾波和加權平均，結果如圖5所示，誤差對比結果見圖6。

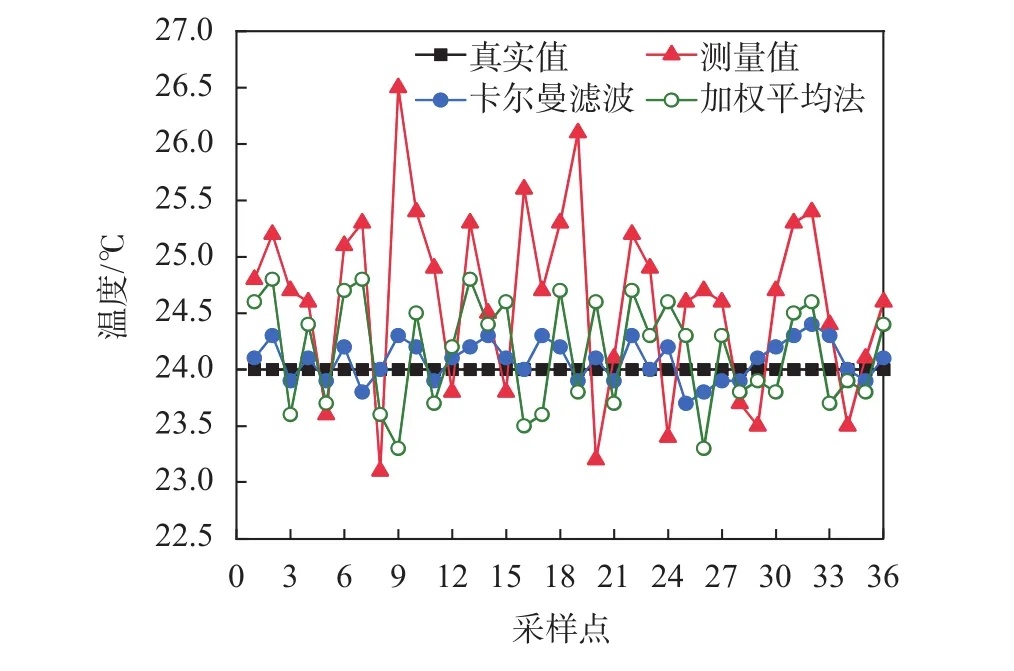
圖5 溫度傳感器的卡爾曼濾波和加權平均對比圖

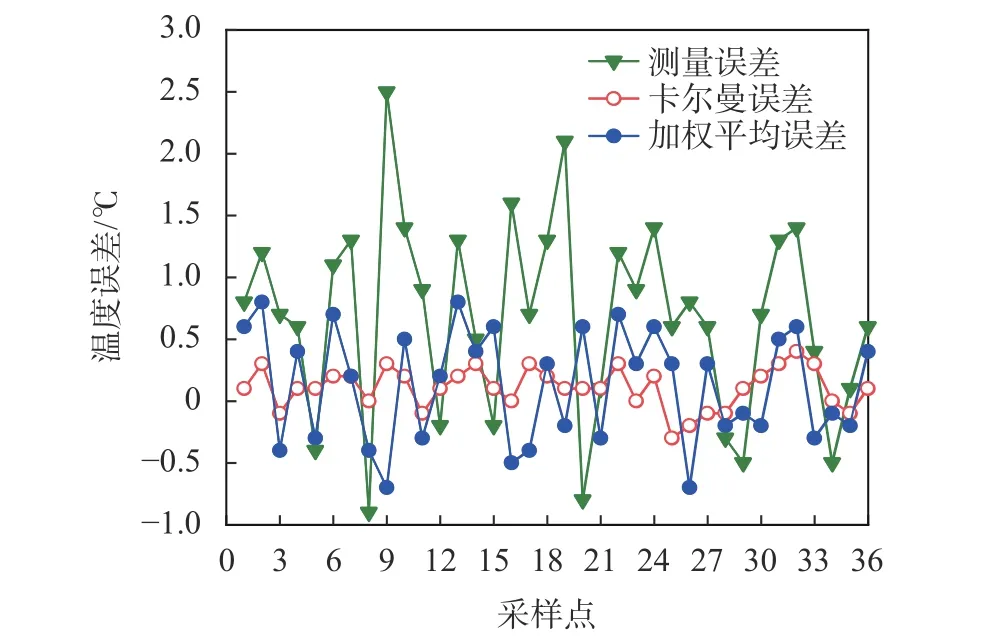
圖6 溫度誤差對比圖

通過計算得出，同質傳感器經過卡爾曼濾波算法處理后的值為24.08 ℃，而36組數據的平均值為24.61 ℃，經過加權平均算法處理后溫度傳感器測量值為24.15 ℃。用標準值24 ℃來對比卡爾曼濾波算法和加權平均算法的精確度，由圖4可以看出經過卡爾曼濾波算法處理后的測量值更接近真實值，由此可以得出卡爾曼濾波算法的優越性與準確度。

圖6為卡爾曼濾波和加權平均處理后的誤差結果比對圖，通過計算得出卡爾曼濾波的誤差為0.335%，測量誤差為 2.51%，加權平均誤差為0.636%，顯示了卡爾曼濾波算法處理數據的能力，經過卡爾曼濾波后的誤差相對于測量誤差和加權平均誤差都較小，這表明卡爾曼濾波算法滿足同質傳感器融合過程中對數據處理的要求。

3 異質傳感器融合算法

單一傳感器獲得的僅是環境特征的局部、片面的信息，它的信息量是非常有限的。而且每個傳感器還受到自身品質、性能及噪聲的影響，采集到的信息往往是不完善的，具有較大的不確定性。因此，通過不同傳感器采集的環境信息進行融合可以獲取更加豐富且有效的環境信息，消除了單因子傳感器對環境監測的簡單性和局限性，提高整體環境監測的可靠性和準確性。

3.1 BP神經網絡

BP網絡又稱反向傳播神經網絡，通過對數據樣本的訓練，不斷修正網絡的權值和閾值使誤差函數沿著負梯度方向下降，逼近期望輸出。在運用過程中網絡也存在著不足，如網絡的收斂速度較慢，訓練易陷入癱瘓，不具有全局搜索能力，容易出現局部極小值[12]。此時引入具備運行速度較快、全局尋優能力較好的粒子群算法（PSO）來解決傳統BP神經網絡易陷入收斂速度較慢，訓練易陷入癱瘓以及容易出現局部極小值的問題[13]。

建立室內環境多傳感器數據監測的BP神經網絡模型，輸入層為4種傳感器采集的5種環境數據參數，隱含層神經元節點數可以根據經驗公式（6）來確定數量范圍，輸出層為5種環境參數的真實值。3層BP神經網絡如圖7所示。

圖7 設定的3層BP神經網絡

BP神經網絡中隱含層的激活函數為sigmoid，輸出層的傳遞函數為purelin，用下兩式表示：

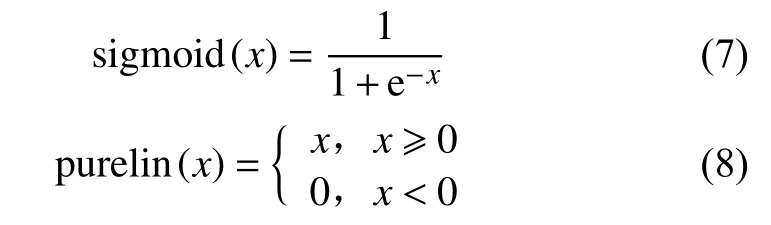
通過采集室內環境參數進行BP神經網絡的模式訓練，共采集800個數據樣本，隨機選擇500個作為訓練樣本，剩余300個數據作為測試樣本。根據式（6）來采用試錯法確定隱含層神經元個數，其平均相對誤差對比結果如表1所示。結果表明，神經元個數為10時，3種氣體的平均相對誤差最小。最終選取隱含層神經元節點個數為10。

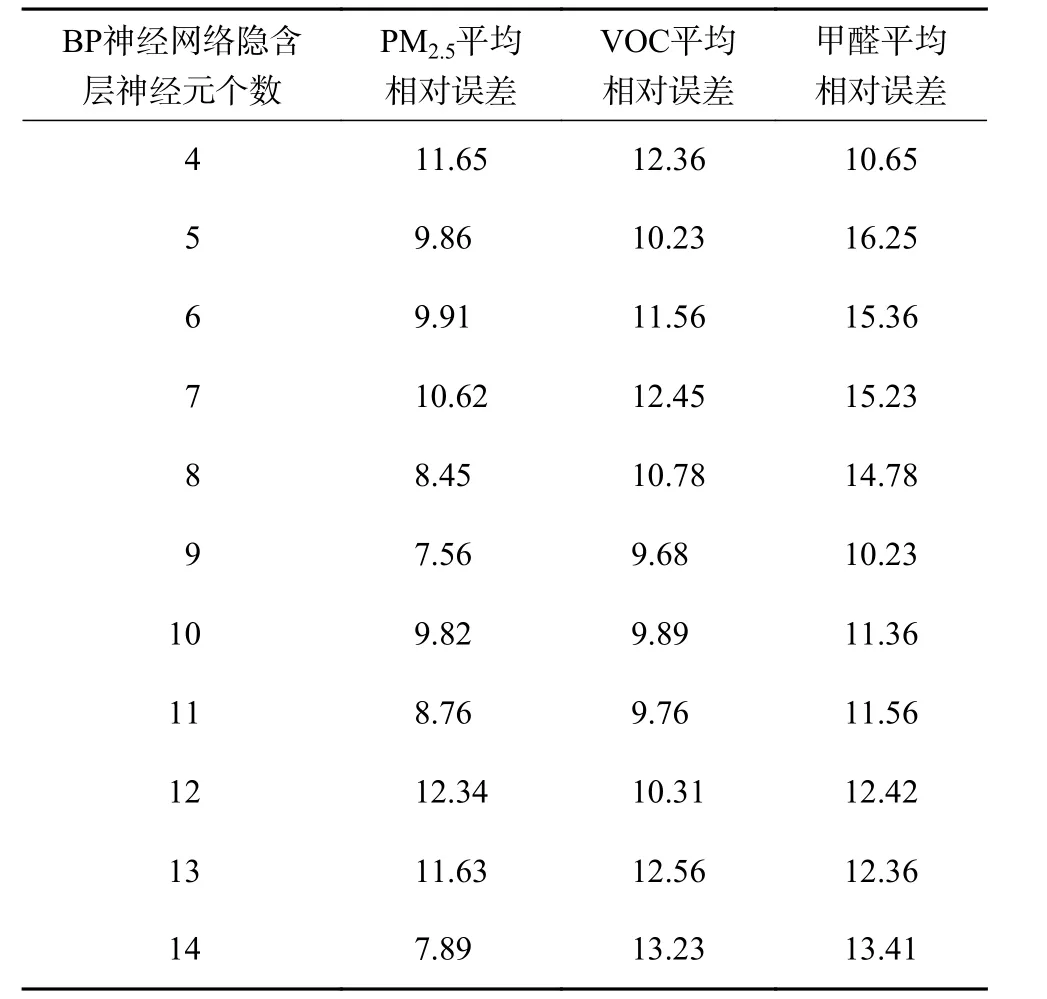
表1 不同隱含層神經元數的神經網絡輸出值和與真實值的平均相對誤差 %

3.2 PSO優化BP神經網絡模型

粒子群（particle swarm optimization，PSO）算法是模擬鳥類覓食行為的一種新的進化計算方法。PSO是基于粒子迭代尋找空間的最優解的一種全局動態尋優計算方法，通過在每次迭代過程中尋求全局最優和個體極值來不斷調整自己的位置和速度[14]。其迭代公式為：

經過多次實驗訓練，設置粒子最大迭代次數為150，種群規模設置為40，慣性因子設置為0.8，學習因子和均為2。由圖8可知，PSO-BP神經網絡在迭代次數為100時達到最優。

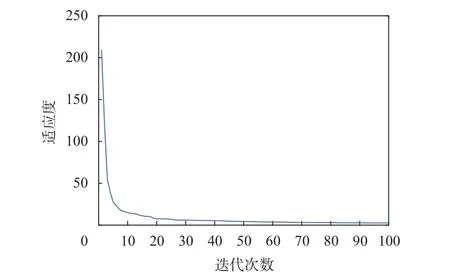
圖8 適應度曲線

BP神經網絡會由于初始值閾值和權值選取的不合理，導致收斂速度較慢，訓練易陷入癱瘓，不具有全局搜索能力，容易出現局部極小值，同時進行大量的網絡訓練，易造成過度擬合針。利用PSO算法對BP神經網絡網絡進行優化，解決BP神經網絡的不足，經過反復多次的實驗最終確定BP神經網絡的閾值和權值。PSO-BP神經網絡算法流程圖如圖9所示。

圖9 PSO優化BP神經網絡算法流程圖

4 融合算法分析對比驗證

4.1 算法性能指標

為了評估BP神經網絡模型、PSO-BP神經網絡模型和AW-BP神經網絡模型的性能，本文采用平均絕對百分比誤差（MAPE）和擬合度(r2)對算法模型進行評價。其計算公式如下：

4.2 驗證結果及分析

在室內各個房間布置傳感器，傳感器每隔2 min采集一次環境信息，為了將經過多傳感器融合算法處理后的值和環境氣體真實值做對比，采用德國進口元特SHY-6000型精密手持測量儀對室內各個房間進行環境數據采集，將手持儀采集到的數據作為室內環境的真實值。傳感器共采集室內環境數據800個，分別用BP神經網絡模型、粒子群（PSO）優化BP神經網絡模型以及自適應加權（AW）優化BP神經網絡模型對500個數據樣本進行訓練，經過反復的訓練以及調整參數完成上述三種算法網絡模型的訓練，保存網絡并對剩下的300個測試樣本數據進行測試。為了能夠在圖中清晰的展示結果，隨機選取20個樣本數據作圖，測試結果如圖10～圖12所示。

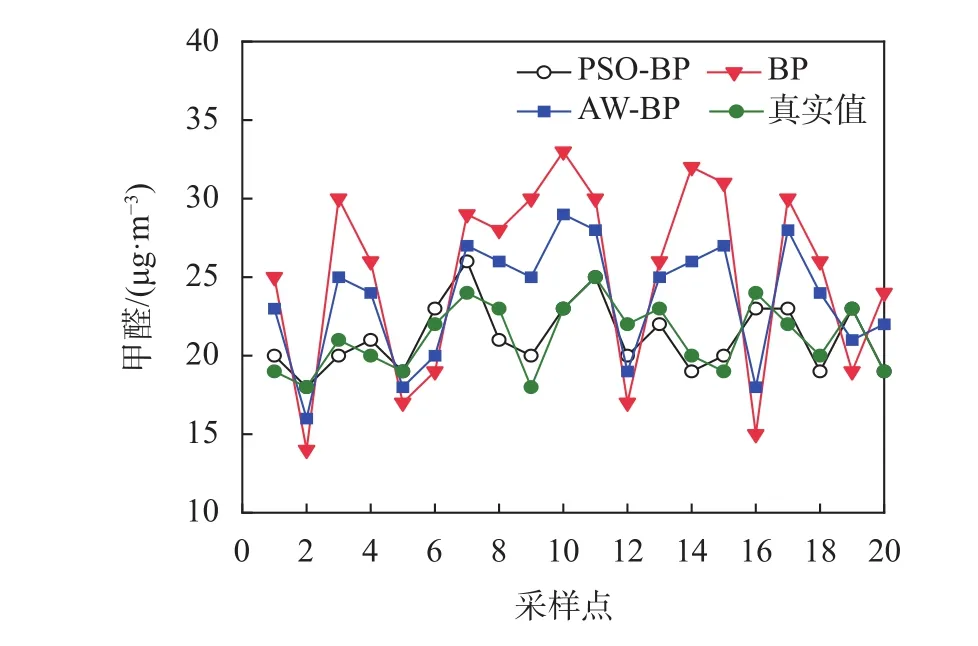
圖10 甲醛對比圖

圖11 PM2.5對比圖

圖12 VOC對比圖

由圖可知，自適應加權（AW）優化BP神經網絡模型處理后的數據比BP神經網絡模型處理后的數據更接近真實值，用PSO優化BP神經網絡模型處理后的數據比自適應加權（AW）優化BP神經網絡模型處理后的數據更接近真實值，證明了本文所提出PSO-BP神經網絡算法具有更高的融合精度。

使用Matlab的profiler計算三種算法運行150次的平均運行時間，結果如表2所示。

表2 三種算法平均運行時間

從表2可以看出，PSO-BP算法的平均運行時間比BP算法短69.31%，比AW-BP算法短50.36%，大大提高了算法的性能，能夠有效降低傳感器節點的能耗，延長傳感器壽命。

為了進一步分析和比較不同融合算法的融合性能，本文以平均絕對百分比誤差（MAPE）和擬合度r2對算法模型進行對比分析。表3為三種算法模型對300組測試樣本進行測試下MAPE和r2結果，由表3可知：PSO-BP算法模型在平均相對誤差和擬合度兩種性能指標上均優于BP算法模型和自適應加權（AW）優化BP算法模型。經過PSO優化BP神經網絡后甲醛、PM2.5、VOC的平均絕對百分比誤差為4.13%、3.41%、3.25%，具有良好的優化效果。

表3 三種算法模型的性能比較

5 結束語

針對多傳感器數據融合精度低、穩定性差的問題，提出了一種基于PSO優化BP神經網絡多傳感器數據融合算法。從實驗數據分析發現：1）經過防脈沖干擾平均濾波算法的數據預處理和卡爾曼濾波算法的同質傳感器數據融合，可以有效地減少數據波動，得到最優數據集，提高了系統的穩定性。2）與BP神經網絡和自適應加權（AW）優化BP神經網絡算法相比，基于PSO優化BP神經網絡融合算法具有更短的平均運行時間和更高的數據融合精度。綜上所述，本文提出的數據融合算法具有良好的適用性，能夠滿足室內環境監測系統的數據融合要求。