活塞發動機止動輪轂傳動系統動態特性分析

胡 瓏，黃 友，周 丹，宋朝省，魏長旭

(1.重慶大學 機械傳動國家重點實驗室，重慶 400044；2.重慶宗申航空發動機制造有限公司，重慶 400054)

止動輪轂傳動系統作為活塞發動機動力系統的重要組成部分，是保證發動機正常工作的關鍵部件，其動態特性直接影響發動機可靠性和穩定性。然而，由于發動機止動輪轂系統存在嚙合面幾何形貌復雜、動態接觸機理不清及載荷工況復雜等問題，其振動沖擊問題一直是困擾活塞發動機整體動態系統提升的關鍵因素之一，所以開展止動輪轂傳動系統動力學建模與動態特性分析研究對揭示活塞發動機止動輪轂傳動系統振動機理，提升整機性能具有重要的理論意義與工程應用價值。

近年來國內外學者針對活塞發動機動力裝置、起動特性和增壓特性等進行了一定的研究。鮑夢瑤等[1]建立了發動機與渦輪增壓器的系統仿真模型，提出了一種能實現對增壓器失效關鍵影響因素分級的分析法。徐斌等[2]通過研究發動機的增壓性能，提出了基于實驗的活塞發動機二級增壓壓比分配方案的方法。王兆銘等[3]基于某型航空發動機研究平臺，討論了高原環境下的起動供油控制規律。Moorthy等[4]建立了能實時、準確地反映真實發動機運行工況的航空活塞發動機模型，并進行了模擬仿真。Singla等[5]為了改善某型號發動機的性能，對其進氣歧管開展了研究。Crosbie等[6]開展了一定壓力和溫度范圍下的發動機高空性能測試實驗，提出了安裝節氣門燃料噴射系統能讓發動機的高空性能得到提升的方法。

筆者在分析活塞發動機止動輪轂系統結構和工作原理的基礎上，建立了止動輪轂傳動系統三維實體模型和解析動力學模型；采用Adams多體動力學軟件建立了止動輪轂傳動系統動力學仿真模型，通過對比分析，相互驗證了動力學模型正確性，在此基礎上研究了不同軸向預緊力和扭矩工況對止動輪轂系統動態特性的影響規律。

1 發動機止動輪轂傳動系統結構與工作原理

活塞發動機止動輪轂傳動系統三維模型如圖1所示，主要由輸出軸、止推半環、小齒輪、螺旋槳齒輪與止動輪轂組成。其中，螺旋槳齒輪與輸出軸連接部分軸上有套筒，螺旋槳齒輪與小齒輪間連有墊圈，止動輪轂與3個串聯的碟簧相連，受到碟簧的軸向預緊力。止動輪轂傳動系統結構如圖2所示。

圖1 止動輪轂傳動系統三維模型Fig.1 Three-dimensional model of doghub transmission system

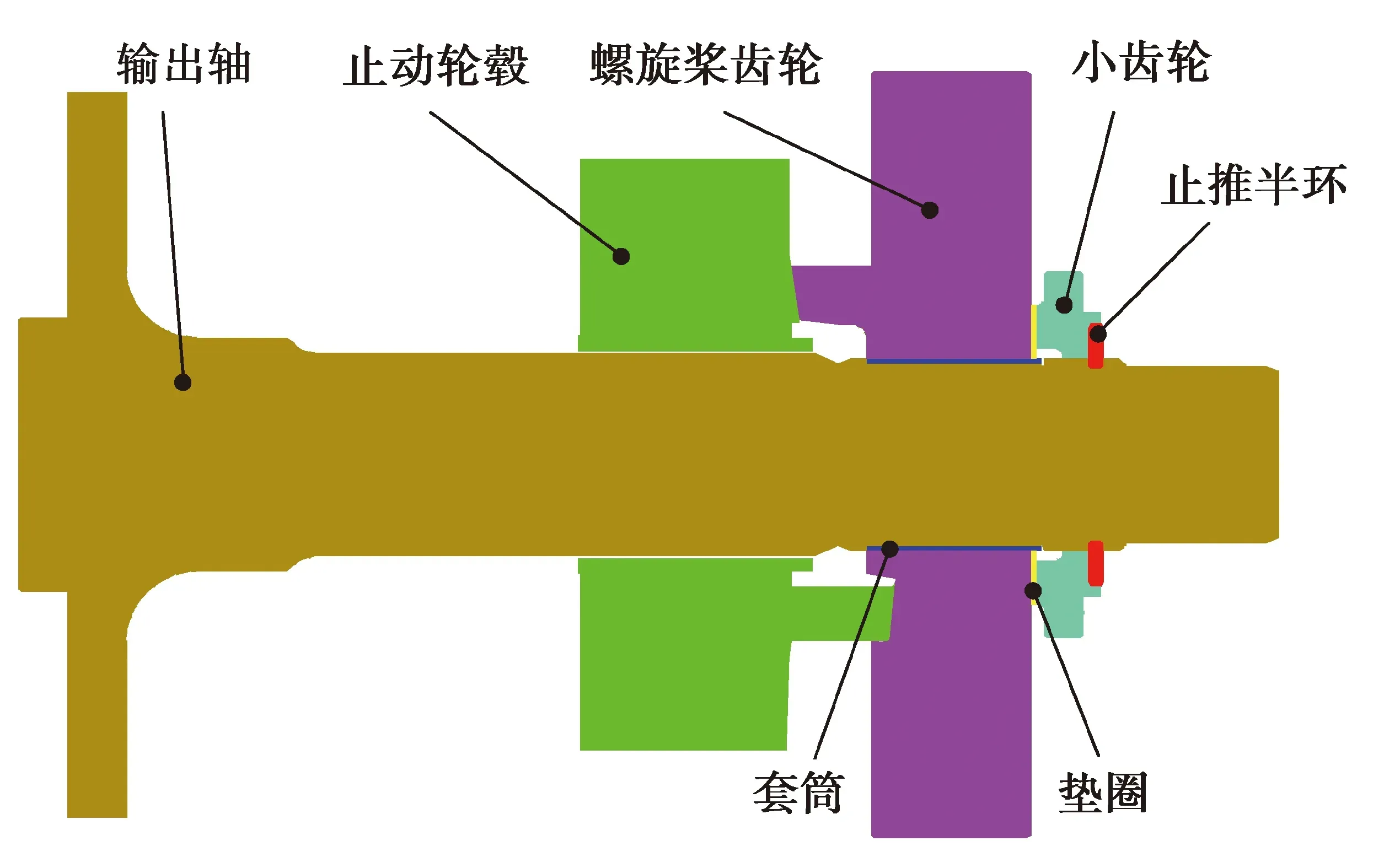
圖2 止動輪轂傳動系統結構圖Fig. 2 Structure diagram of doghub transmission system

止動輪轂傳動系統各零件材料具體參數如表1所示。

表1 材料參數

續表1

止動輪轂傳動系統工作原理如圖3所示，其動力來源于與曲軸固連的動力輸入齒輪，通過與螺旋槳齒輪嚙合傳遞到螺旋槳齒輪，螺旋槳齒輪再與止動輪轂通過曲面接觸將動力傳遞到止動輪轂，最后由止動輪轂通過花鍵連接將動力傳遞到輸出軸，完成止動輪轂傳動系統的整個動力傳遞過程。

圖3 系統動力傳遞路線Fig. 3 Transmission route of system power

止動輪轂與螺旋槳齒輪的動力傳遞通過其三爪曲面接觸傳遞，如圖4所示。當系統啟動時，螺旋槳齒輪繞輸出軸轉動，其凸爪頂部與止動輪轂凸爪底部相接觸，由于螺旋槳齒輪軸向位移自由度被止推半環限制，在接觸力的作用下，止動輪轂凸爪沿著螺旋槳齒輪凸爪的曲面軸向移動，從螺旋槳齒輪凸爪底部的過渡圓弧段“爬坡”到凸爪工作斜面段，最后穩定在工作斜面與螺旋槳齒輪一同旋轉。當穩定在工作斜面段后，止動輪轂接觸副的受力情況如圖5所示(圖中下標p表示螺旋槳齒輪，g表示止動輪轂)。其中，AB段為過渡圓弧段，BC段為工作斜面段。

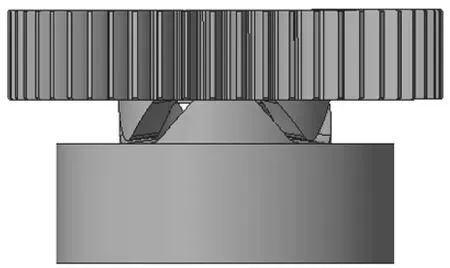
圖4 止動輪轂螺旋槳齒輪接觸副Fig. 4 Doghub-airscrew gear contact pair

圖5 止動輪轂接觸副受力圖Fig. 5 Force diagram of doghub contact surfaces

2 止動輪轂傳動系統解析動力學模型

圖6 止動輪轂系統動力學模型Fig. 6 Dynamic model of the doghub system

如圖6所示，設螺旋槳齒輪p為主動輪，止動輪轂g為從動輪，三爪斜面的傾角為α，三爪的動力學模型建立在中間平面上，其等效接觸半徑可表示為

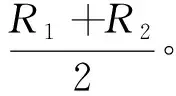
(1)

系統的廣義位移列陣δ可表示為

δ={xpθpxgθg}T,

(2)

式中xi，θi(i=p,g)分別為主、從動輪在x向的平移振動位移和軸向振動位移。

系統的動能為

(3)

系統的勢能、耗散能分別為

(4)

(5)

式中：δ為各方向投影到嚙合線上的變形量，變形量壓縮方向定義為正；Kix、Cix分別為主、從動輪的支撐剛度和阻尼；Km，cm分別為主從動輪嚙合處的嚙合剛度和嚙合阻尼。

其中x，θ方向振動投影到嚙合線方向的變形量分別為

δx=(-xp+xg)cosα，

(6)

δθ=(-Rpθp+Rgθg)sinα。

(7)

則系統各向振動投影到嚙合線方向的總變形為

δ=δx+δθ=(-xp+xg)cosα+(-Rpθp+Rgθg)sinα，

(8)

(9)

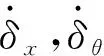
xp方向受到的外力為

(10)

θp方向的力矩為

(11)

xg方向受到的外力為

(12)

θg方向產生的力矩為

(13)

根據拉格朗日能量方程

(14)

則有

通過有限元求得模型的嚙合剛度為

km=1.245×1013N/m。

3 止動輪轂系統動力學仿真模型

基于Adams多體動力學軟件平臺，進行止動輪轂系統動力學仿真模型的建立以及后續的仿真分析。動力學仿真模型的建立具體如下：

1)首先將系統中各個零件三維模型導入，分別進行位置坐標的變換，使零件的幾何旋轉軸線位于Z軸上，方便后續邊界的建立。然后將各個零件按照對應關系進行裝配。

2)設定模型的材料屬性。將模型從三維軟件導入后，會丟失零件材料的物理屬性，所以需要按表1參數分別賦予各個零件的材料屬性。

3)設置模型運動副約束。止動輪轂系統各個零件約束條件如表2所示。

表2 模型的約束關系

5)定義各個零件之間的接觸時，選擇基于碰撞函數的接觸算法,接觸類型選擇Solid to Solid，摩擦類型選擇Coulomb。其中接觸參數主要包括材料接觸剛度、力指數、接觸阻尼、穿透深度以及動摩擦系數,具體接觸參數取值如表3所示。

表3 接觸參數

設置完成后的止動輪轂系統動力學仿真模型如圖7所示。

圖7 系統動力學仿真模型Fig. 7 System dynamics simulation model

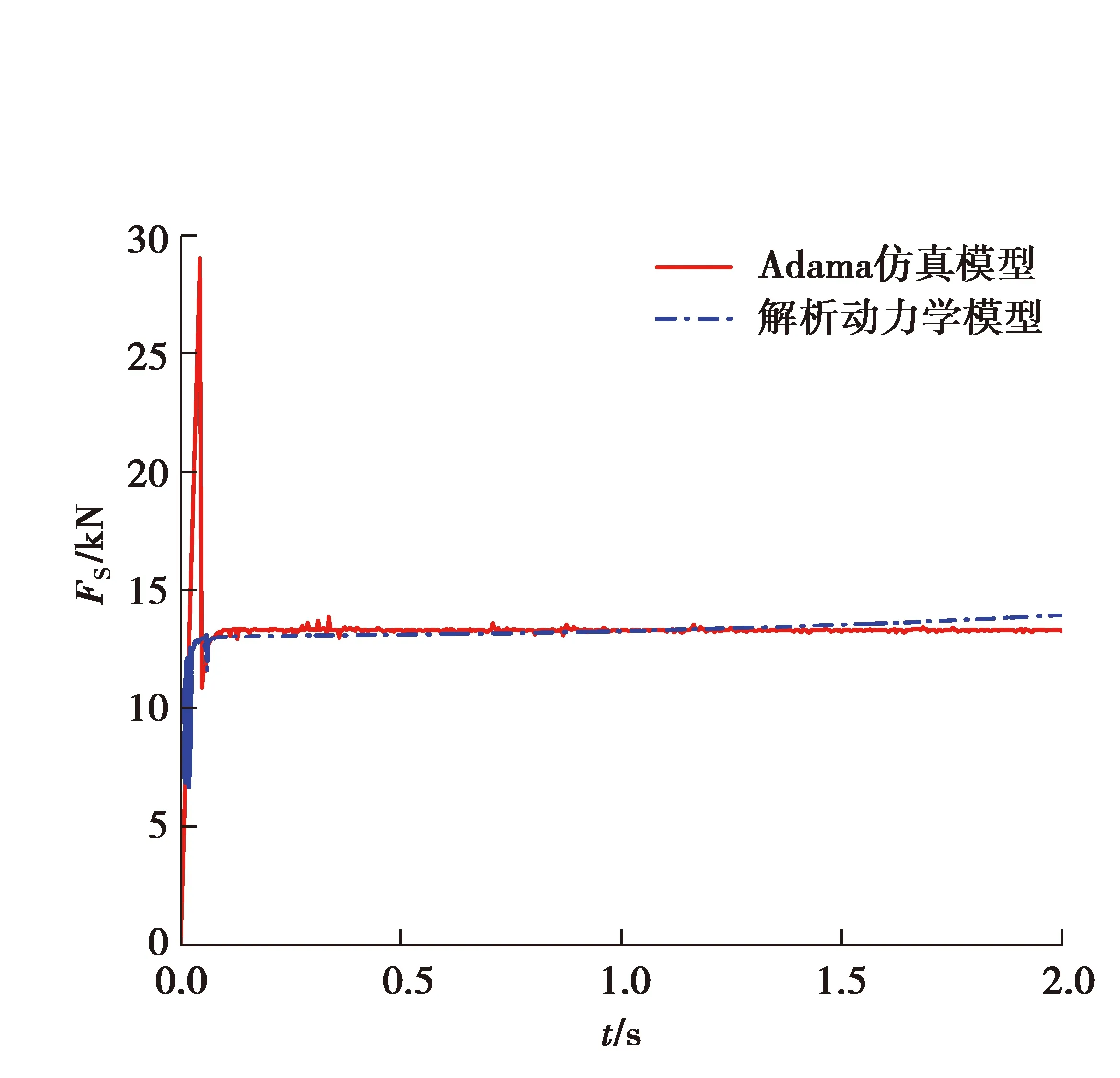
圖8 兩種模型軸向力結果對比Fig. 8 Comparison of axial force results of two models

由圖8可知，在額定工況下，解析動力學計算出的軸向力更快地趨于平穩，最后穩定在13 942 N附近小幅波動，Adams計算的軸向力在初始階段波動較大，然后逐步趨于平穩，最后穩定在13 300 N附近小幅波動。解析動力學的計算結果與Adams的計算結果對比，在穩定之后的誤差約為4.6%，相互驗證了動力學模型的正確性。

4 動態特性分析

為揭示活塞發動機止動輪轂傳動系統振動機理，在額定轉速下，進行不同扭矩和不同軸向預緊力對止動輪轂系統動態特性的影響分析。其中額定輸入轉速如圖9所示。

圖9 額定輸入轉速Fig. 9 Rated input speed

4.1 不同扭矩對系統動態特性的影響分析

圖10 不同扭矩下的止動輪轂軸向力Fig. 10 Axial force of doghub under different torques

圖11 不同扭矩下的止動輪轂軸向位移Fig. 11 Axial displacement of doghub under different torques

圖12 350 Nm扭矩的止推半環軸向力Fig. 12 Axial force of thrust ring under 350 Nm torque

圖13 500 Nm扭矩的止推半環軸向力Fig. 13 Axial force of thrust ring under 500 Nm torque

表4 不同扭矩下的仿真結果

4.2 不同軸向預緊力對系統動態特性的影響分析

圖14～18為系統在3種不同軸向預緊力工況下的動態特性結果。結果表明，系統啟動階段，止動輪轂由過渡圓弧段爬坡到工作斜面段過程中，止動輪轂軸向沖擊力波動較大,在6 000，7 000和8 000 N軸向預緊力工況下的沖擊力峰值分別可達28.56，29.21，30.6 kN；在爬坡到工作斜面穩定后，其軸向力波動很小，分別穩定在12.38，12.42和12.6 kN左右。止推半環所受軸向沖擊力趨勢與止動輪轂軸向力趨勢相似，在6 000，7 000和8 000 N軸向預緊力工況下，止推半環軸向力沖擊峰值分別可達8.36 kN/8.04 kN、8.63 kN/8.02 kN和9.34 kN/8.35 kN；止動輪轂軸向位移則在止動輪轂爬坡到工作斜面后分別穩定在4.19，3.63和3.24 mm。

圖14 不同軸向預緊力下的止動輪轂軸向力Fig. 14 Axial force of doghub under different axial preloads

圖15 不同軸向預緊力下的止動輪轂軸向位移Fig. 15 Axial displacement of doghub under different axial preloads

圖16 6 000 N軸向預緊力下的止推半環軸向力Fig. 16 Axial force of thrust ring under 6 000 N axial preload

圖17 7 000 N軸向預緊力下的止推半環軸向力Fig. 17 Axial force of thrust ring under 7 000 N axial preload

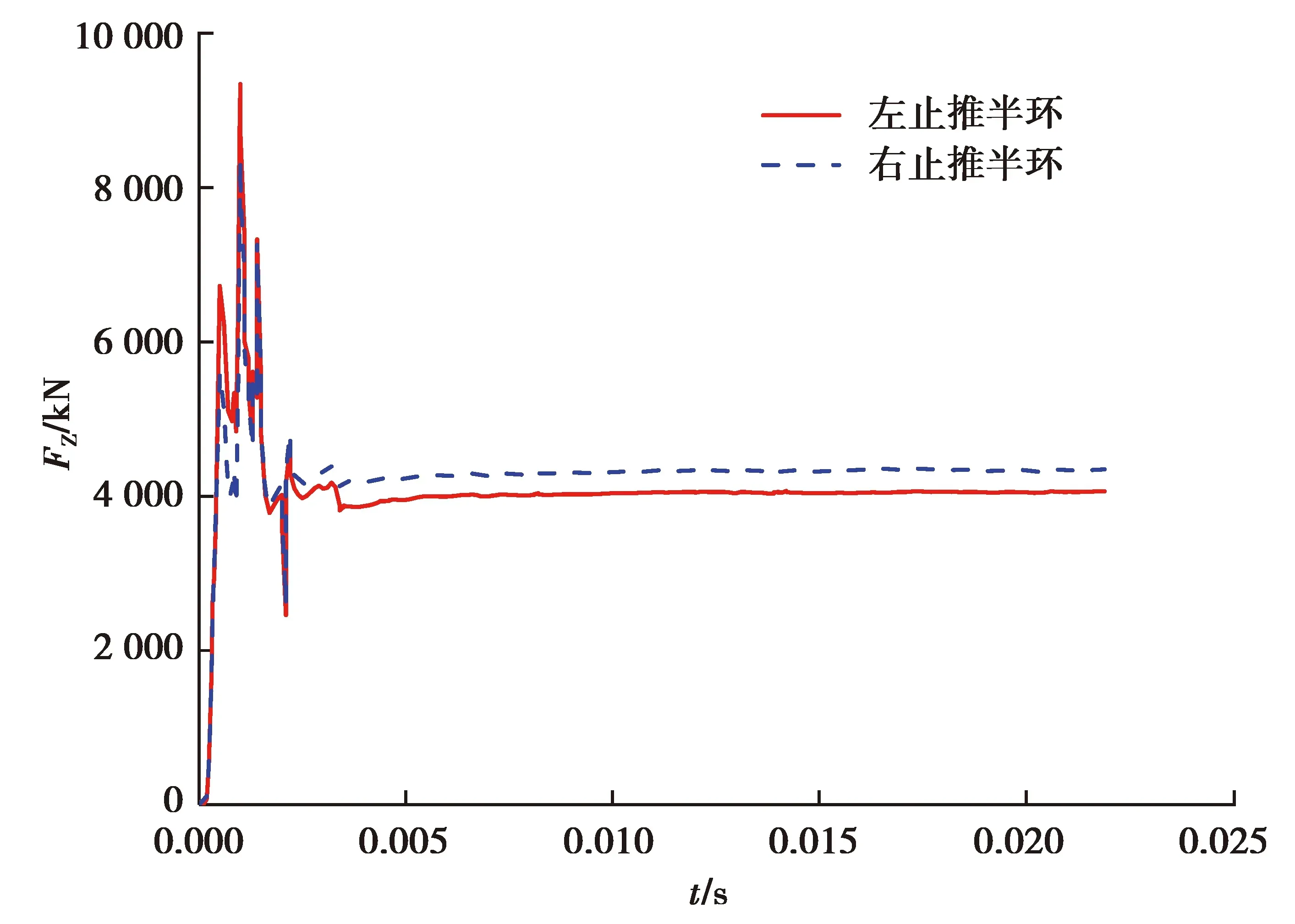
圖18 8 000 N軸向預緊力下的止推半環軸向力Fig.18 Axial force of thrust ring under 8 000 N axial preload

對比6 000，7 000和8 000 N 3種不同軸向預緊力下的仿真結果如表5所示。

表5 不同軸向預緊力下的仿真結果

從表中可以看出，軸向預緊力由6 000 N逐步增大到8 000 N，止動輪轂軸向力有所增大，系統啟動爬坡階段的軸向沖擊峰值由28.56 kN增大到30.60 kN，爬坡到工作斜面穩定后的均值由12.38 kN增大到12.60 kN；止推半環所受軸向沖擊力趨勢與止動輪轂軸向力相似，止推半環所受軸向沖擊力也明顯隨著軸向力的增大而增大，沖擊峰值由8.30 kN/8.00 kN增大到9.30 kN/8.30 kN，均值由3.99 kN/4.26 kN增大到4.04 kN/4.32 kN。止動輪轂軸向位移則明顯減小，由4.19 mm減小到3.24 mm；所以，相對于額定8 000 N軸向預緊力，適當減小軸向預緊力能一定程度上減小系統所受軸向沖擊力。

5 結 論

在分析發動機止動輪轂系統工作原理的基礎上，提出了止動輪轂三爪曲面接觸系統動力學建模與分析方法，研究了不同扭矩和軸向預緊力工況對止動輪轂系統軸向沖擊力與位移的影響規律，主要結論如下:

1)在止動輪轂由過渡圓弧段爬坡到工作斜面過程中，止動輪轂與止推半環所受軸向力波動較大且會達到峰值；在止動輪轂爬坡完穩定在工作斜面轉動后，止動輪轂與止推半環所受軸向力波動很小，基本趨于穩定。

3)隨著軸向預緊力增大，止動輪轂軸向力與止推半環所受軸向力在系統啟動階段與穩定階段都有所增大，止動輪轂軸向位移則明顯減小。因此適當減小軸向預緊力能一定程度上減小系統所受軸向振動沖擊。