縱向組學數據統計分析方法和研究策略*

呂嘉麗 范冰冰 魏夢珂 張 濤△

近年來，隨著高通量檢測技術與機器學習方法的發展，以前瞻性隊列設計為基礎的縱向組學研究已經成為系統生物學研究新趨勢[1]。統計學上，縱向數據統計分析方法已經形成了系統的統計分析框架，但這些方法主要集中于變量數目小于觀察單位數的低維醫學縱向數據[2]。而針對縱向組學數據，目前仍缺乏成熟的統計分析策略。本文擬對近年來國內外研究者提出的縱向組學數據統計分析方法進行介紹，并系統地總結各個方法的核心思想及優缺點，給出縱向組學數據統計分析策略。

縱向組學研究設計與數據特點

在不同的生命及疾病狀態下，機體組學標記物濃度處于連續動態變化過程。縱向組學研究設計是指在疾病發生發展過程中或采取干預措施后采集多個時間點的生物標本，進行高通量組學檢測。該研究設計可以分析組學標記物的動態變化規律，探討生物體對危險因素累積的反應過程及疾病發生發展機制。

在數據特點上，縱向組學數據包含個體、時間、組學標記物、相關暴露因素及結局測量信息(如表1所示)。縱向組學數據具有以下特征：(1)非平衡性：不同觀察單位隨訪時間點不一樣，同一觀察單位間的隨訪間隔也不一樣；(2)自相關性：同一觀察單位的不同測量變量之間具有復雜的相關與因果調控關系；(3)測量誤差：組學研究常常需要借助高通量檢測儀器完成生物樣本測量，數據集難免存在由于測量誤差引起的變異；(4)時依混雜：在縱向組學研究中，組學測量數據及環境暴露因素均隨時間而動態變化，會對因果效應估計產生影響；(5)高維災難：縱向組學數據除具有一般縱向數據特點外，還存在一般高維小樣本組學數據的高維災難問題。

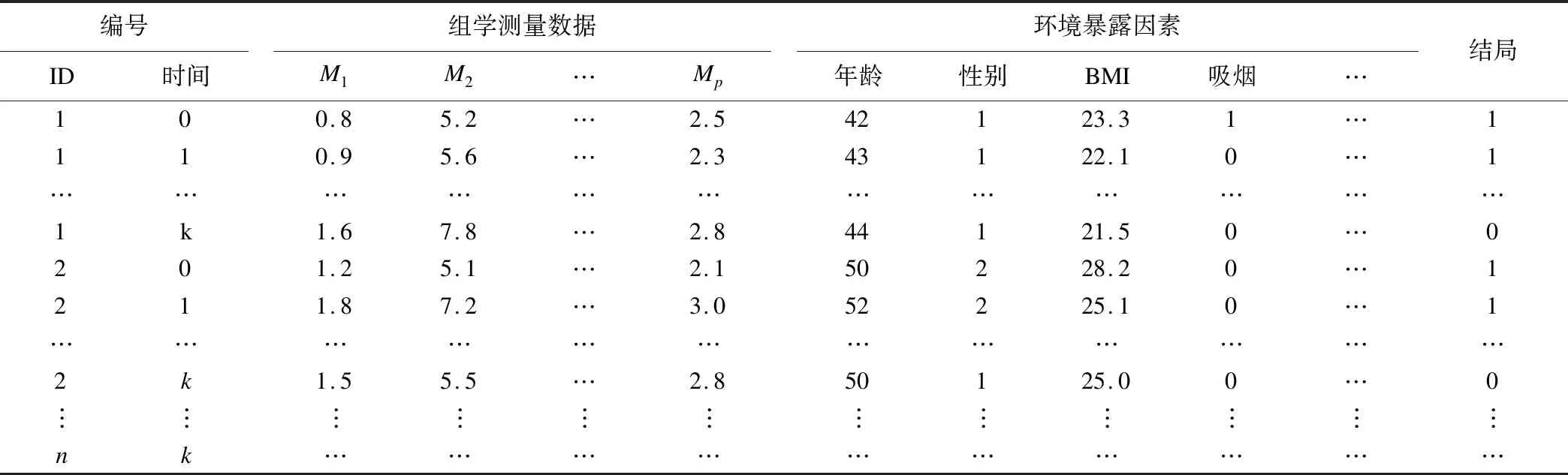
表1 縱向組學數據結構

縱向組學數據常用統計分析方法

縱向組學研究設計的研究目的包括：(1)研究不同組別間組學標記物的動態輪廓差異，發現不同組別間的動態差異組學標記物；(2)研究組學標記物隨時間變化的動態趨勢；(3)基于動態差異組學標記物，建立預測模型。根據上述研究目標及數據特點，常見縱向組學設計分析方法主要有以下三類[3-5]：(1)單變量統計分析：用于識別隨時間變化而改變的差異動態標記物；(2)聚類方法：對標記物的動態變化進行趨勢分析，對變化趨勢一致的標記物進行聚類；(3)降維方法：考慮到變量間的復雜相關性，利用多變量統計分析方法對高維小樣本數據進行降維，發現組學標記物在不同組別間的組學輪廓差異。

1.單變量分析

重復測量方差分析(repeated measures ANOVA) 是早期用于縱向數據分析的方法[6]。目前，混合效應模型(mixed effects models)及廣義估計方程(generalized estimating equations)是縱向組學數據分析的常用單變量統計方法[2]。曹紅艷等[7]在廣義估計方程基礎上提出了一種懲罰廣義估計方程(penalized generalized estimating equations)，并運用該方法對小鼠進行糖尿病發病關聯基因位點篩選。該方法的核心思想是基于LASSO或SCAD等懲罰方法進行廣義估計方程建模，不僅保持了廣義估計方程的重要特性，同時將該方法推廣到高維數據分析，適用于協變量個數p隨樣本例數n同階變化的情況。

2.聚類分析

聚類分析(clustering analysis)能同時考察所有變量，識別變化趨勢一致、功能相似的組學標記物，對于生物機制的研究具有重要意義[8]。時間序列聚類(time series clustering)根據時間序列相似度對研究對象進行聚類，從而使不同聚類的類間距離最大，類內距離最小。模糊C均值聚類(fuzzy c-means clustering) 是動態組學研究設計中應用最為廣泛的一種算法[9-10]。其核心思想是對j個觀察單位X={X1，X2…Xj}尋找c個模糊組，并求每組的聚類中心，使得目標函數達到最小。模糊C聚類的優點在于能適應分離性不好的數據集，允許數據性質的模糊性，為數據結構描述提供了詳細信息[11]。一項模擬研究表明，相較于K均值聚類算法，模糊聚類算法具有相對較高的聚類效能[12]。但該算法的性能尚依賴于聚類個數和初始隸屬度矩陣。

3.降維分析

常用于組學數據的降維方法包括主成分分析(principal component analysis，PCA)、偏最小二乘判別分析(partial least squares-discriminant analysis，PLSDA)與平行因子分析(parallel factor analysis)等[3]。然而，這些降維方法均未將縱向組學數據集的時間順序信息納入模型，即打亂時間順序后仍然能得到相同的結果，且并不適用于非線性組學數據[13]。目前，已開發的降維方法主要包括基于多水平思想的線性降維方法及基于核函數的非線性降維方法。

(1)線性降維方法

縱向數據具有多水平結構資料的特征，觀察單位為1水平單位，該觀察單位的重復測量資料為2水平單位。多水平模型的核心思想是通過估計兩個水平上的方差，并考慮解釋變量對方差的影響，充分利用各水平內的聚集信息，從而獲得回歸系數的有效估計，提供正確的標準誤與置信區間[14-15]。

多水平同步成分分析(multilevel simultaneous component analysis，MSCA) 是結合多水平思想與主成分分析思想的降維方法[16-17]。多水平同步成分分析模型將數據集總變異分為個體間和個體內兩個水平上的變異。在相同的成分數下，PCA與MSCA相比，解釋的變異相同或更多，對MSCA施加限制越多則解釋變異越小。但MSCA相較于PCA的可解釋度更好，其中不同的亞模型能夠解釋數據中不同的變異，其個體內模型比PCA能更好地展示數據中的動態變異，而個體間模型又比PCA更好地展示個體間的非動態變異。

多水平偏最小二乘判別分析(multilevel PLS-DA，ML-PLS-DA) 的核心思想是將個體間和個體內兩水平的變異分開解釋[18-19]。數據分析時，首先將個體間變異和個體內變異的部分分開，其中個體間變異是對個體兩次測量的均值分析得到，而個體內變異是對個體前后兩次測量的差值進行分析。當使用ML-PLS-DA來描述個體內變異時，主要是關注個體間相同的處理效應。因此，ML-PLS-DA的第一主成分描述主要效應，其后的成分描述個體間不同的處理效應。

(2)非線性降維方法

線性降維方法計算簡便，原理簡單，易于解釋。但該類方法在處理非線性組學數據時，仍然存在一定局限性。為更精確挖掘非線性組學數據信息，研究者在傳統降維分析方法中引入非線性。其中，應用最廣泛的是基于核函數的主成分方法(kernel principal component analysis)[20]，核主成分分析方法將原始數據空間RM中的樣本x映射至特征空間F(Φ：RM→F；x→X)，在特征空間內對樣本X實現主成分分析[20-21]。該方法較傳統主成分分析方法有以下優點[22]：① 引入了非線性映射函數Φ，將原始數據映射至特征空間，能夠更好地解釋原始數據中非線性變異部分；②可使用不同核函數，對不同種類非線性組學數據實現降維；③能提供比主成分分析更多的特征數目，可以最大限度地提取特征信息。與核主成分分析類似，核偏最小二乘判別分析(kernel partial least squares-discriminant analysis)也是利用核函數方法將原始數據映射至特征空間，以描述特征間的非線性關系[23]。除基于核函數的分析方法外，非線性降維方法還包括局部線性嵌入、等距映射、多尺度變換等流形學習方法。

縱向組學數據統計分析策略

縱向組學研究設計在成為研究生命體功能變化有力手段的同時，也給統計分析帶來了新的機遇與挑戰。研究者們在進行縱向組學數據分析過程中，常常忽略了數據集的時序性及相應統計分析方法原理與前提假設，降低了研究結論的可靠性。本文針對縱向組學數據特點，探索了組學統計分析策略，具體總結如圖1所示。

高通量測量技術中的實驗環境、儀器性能及人工操作等均會對數據質量產生影響。因此，組學測量數據變異來源廣泛，除生物變異外，還包括環境影響及測量誤差等。目前常用數據預處理方法包括噪聲濾除、基線校正及標準化處理。

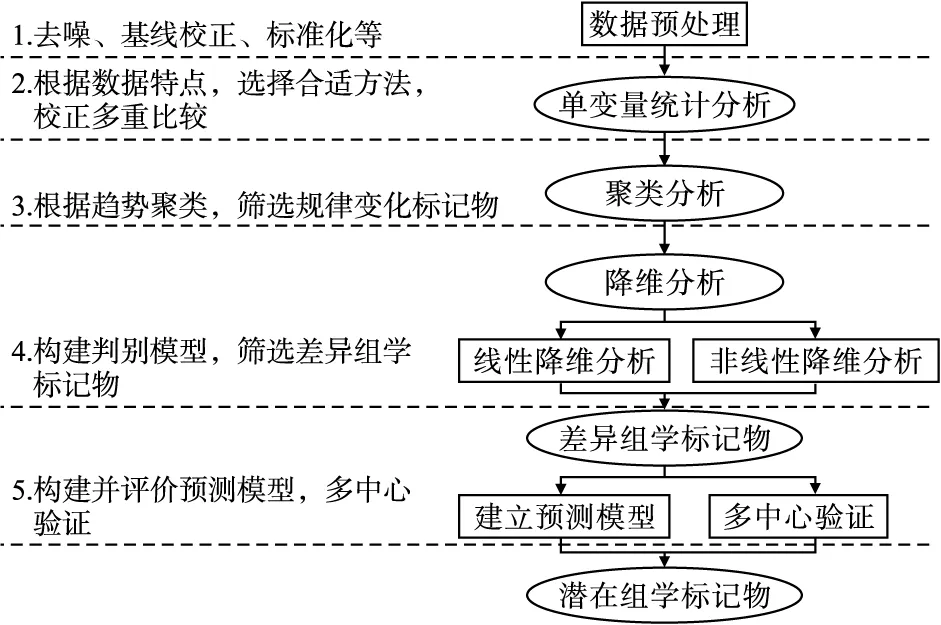
圖1 縱向組學數據統計分析策略流程圖

單變量統計分析思想簡單，易于理解，常用于快速篩選組學研究中隨時間動態變化的組學標記物[24-25]。在單變量統計分析過程中，重復測量方差分析對數據資料要求極為嚴格，須同時滿足方差分析條件及協方差陣球對稱性，混合效應模型及廣義估計方程能考慮到縱向數據的相關性，處理缺失值問題，但后者無法處理高維縱向數據的非平衡性問題，存在一定局限性。此外，高維情境常涉及多重比較問題，需著重考慮對假設檢驗的檢驗水準α進行校正，目前常用校正方法包括Bonferroni校正法及FDR(false discovery rate) 校正法[26-27]。

聚類方法常用于組學標記物時序變化趨勢分析。在經單變量分析后，可通過聚類算法篩選出規律變化的不同類組學標記物，對不同類的組學標記物選擇不同的模型進行研究。K均值聚類算法計算簡便快捷，適應性廣，但在聚類過程中未考慮到縱向數據的時間序列信息；有序樣品聚類大多用于樣品聚類，是一種特殊條件系統聚類算法，但難以直接得出相關序列特征的結論；模糊聚類算法用于時間序列數據時，以時間為維度，計算隸屬度，同時允許了數據性質的模糊性，為數據結構的描述提供了詳細的信息。

主成分分析與偏最小二乘法判別分析是組學研究中常用的降維方法。線性降維方法計算簡便，原理簡單，易于解釋。在降維的同時，考慮到數據的時序信息，能更好地展示數據集的動態變異。非線性降維方法在降維分析中進一步引入非線性，更精確構建判別模型，挖掘非線性數據信息。最終，使用外部測試集評價潛在組學標記物預測效果，探索潛在組學標記物的生物學功能，為分析結果提供合理的生物學解釋。

由于縱向組學數據的復雜特性，上述分析手段能在一定程度上解決組學數據統計分析問題，但仍存在局限性。目前組學標記物變量篩選的方法主要依靠單變量統計分析及后續改進的偏最小二乘法判別分析等方法。數據發生輕微變化時，變量篩選效果也會受到影響，因此建立穩定有效的縱向高維數據變量篩選方法仍然值得研究者們進行探討[28]。此外，利用縱向組學數據進行因果推斷分析時，如何校正時依混雜因素對因果效應估計的影響也需要進一步研究[29-30]。以上兩個關鍵科學問題的解決將會對縱向組學數據提供新的思路與契機。