旋翼飛行器抗風擾控制器設計與風場環境建模

黃夢淵，王耀力，張祉怡，常 青

（1.太原理工大學信息與計算機學院，山西太原 030024；2.北京師范大學 人工智能學院，北京 100875）

無人機廣泛應用在鐵路檢測[1-3]、快遞包裹[4-5]等多個領域。室外風場存在會影響飛行器的飛行姿態和穩定控制性能。使用飛行器實物驗證控制器抗風干擾效果時，容易出現失控，產生危險，增加飛行器研究成本。

國內外學者對相關內容進行了廣泛研究。文獻[6]采用LabVIEW 仿真軟件來顯示飛行器的飛行姿態，但無法模擬風場環境。文獻[7-12]采用EKF濾波對風環境中的飛行器姿態進行實時估計，但抗風干擾能力差。

該文主要研究風場環境下的旋翼動力學模型；設計雙自適應衰減擴展卡爾曼濾波算法(Dual Adaptive Fading Extended Kalman Filter，DAFEKF)來提高姿態數據的濾波精度，并結合PID 控制器來增強系統的抗風干擾能力；對室外風場環境進行分析，建立3D風場仿真模型，進一步驗證系統的控制效果。

1 風場模型

在自然界中往往存在著多種類型的風，通常有平均風、風切變、紊流風、陣風等。但四旋翼飛行器在室外飛行時，通常作用在四旋翼上的主要是紊流風和陣風。對于紊流風，一般用Dryden 模型來產生紊流風。將高斯白噪聲序列通過成形濾波器形成有色噪聲序列，實現對大氣紊流的建模。

Dryden 模型的時間頻譜表示為[13]：

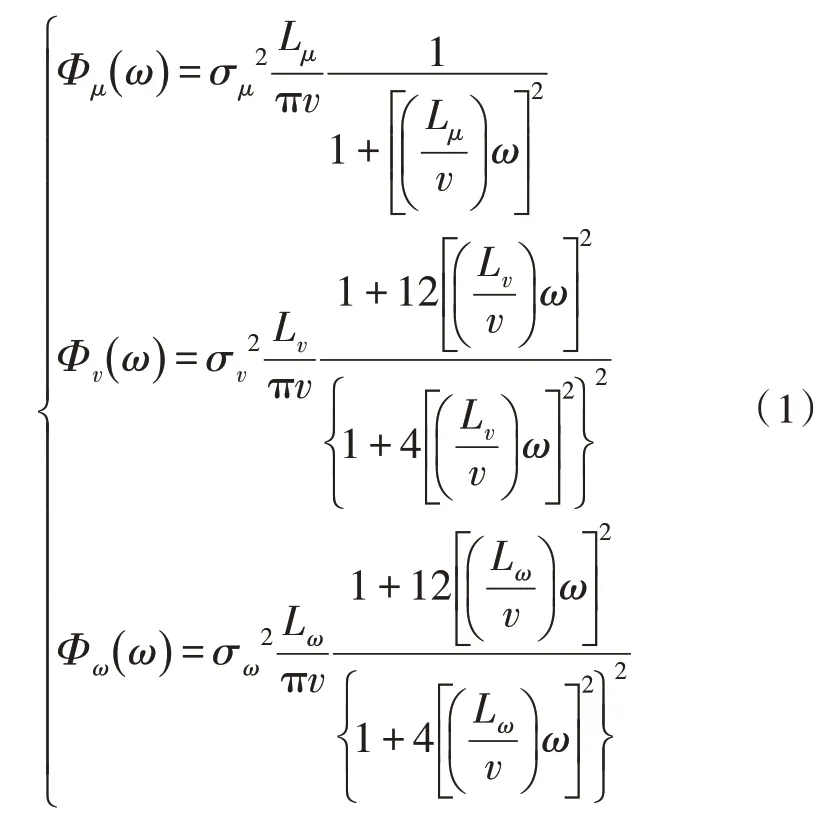
其中，σμ、σv、σω分別表示縱軸、橫軸和豎軸方向的紊流強度，Lμ、Lv、Lω分別表示三軸方向的紊流尺度，v代表旋翼飛行器的飛行速度。由于旋翼飛行器一般都在低空飛行，則依據8785C 規定，紊流強度和紊流尺度可用以下公式得出[13]：

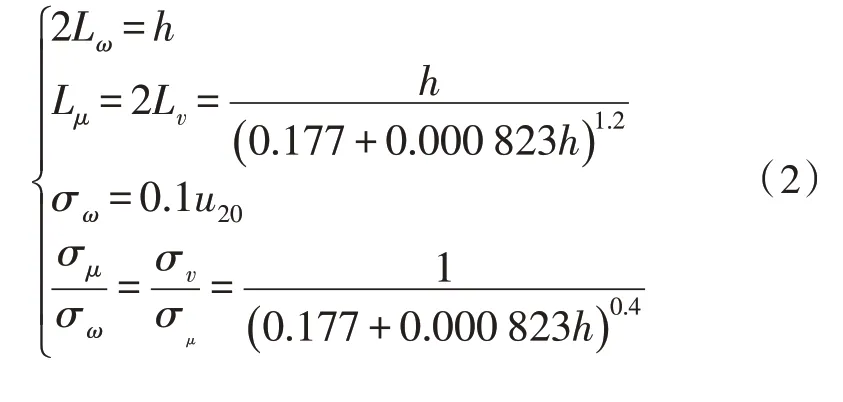
其中，h代表飛行器的飛行高度；u20代表高度為6.096 m 的風速大小。

將單位強度的白噪聲序列通過一個強度為G(s)的成形濾波器，產生的輸出序列的頻譜函數為：

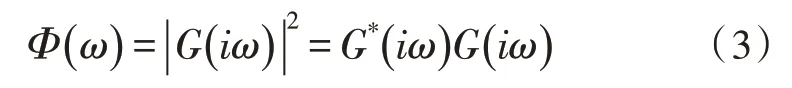
其中，*代表共軛。根據式（3）對式（1）進行分解，可以得到成形濾波器的傳遞函數為[13]:

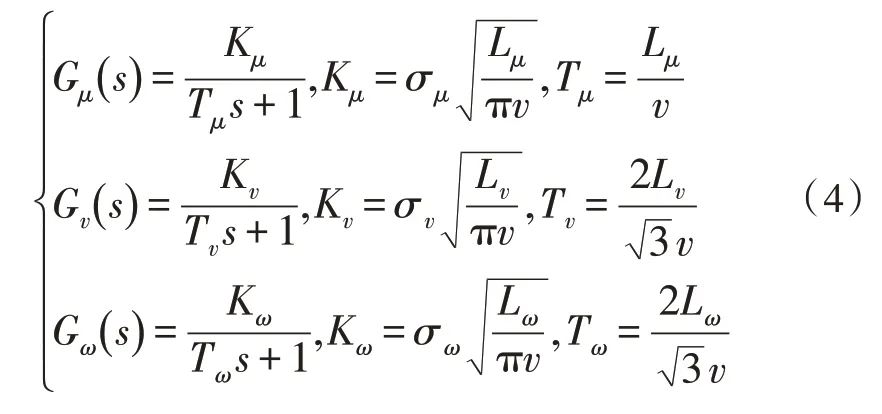
離散突風是指在各個方向上出現忽大忽小的風，又稱陣風。通常用半波離散突風模型表示[14]，如式（1）：

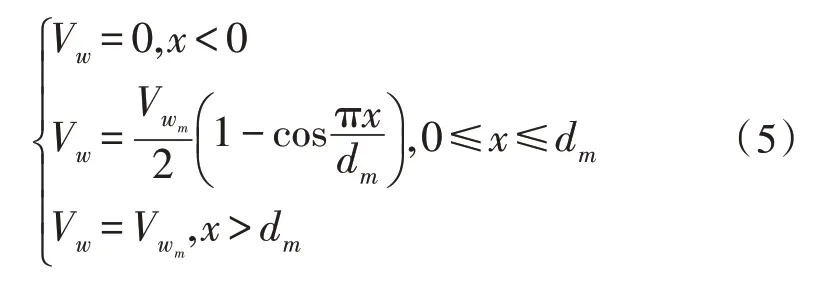
其中，dm為陣風尺度范圍，為陣風峰值，x為距離陣風中心的距離。

將紊流風和陣風相結合可得到真實風場環境，如式（6）：

2 風場中的旋翼動力學模型

2.1 坐標系的建立

四旋翼飛行器在風場環境下進行動力學建模時，首先建立相應的坐標系。該文采取了慣性坐標系O3X3Y3Z3、機體坐標系O2X2Y2Z2、氣流坐標系O1X1Y1Z1。X軸為四旋翼的飛行速度方向，Y軸由右手定則確定，Z軸垂直水平面向上。姿態角度θ、Ψ、φ為俯仰角、偏航角、滾轉角。氣流角α、β為仰角、側滑角。

2.2 動力學建模

通過對四旋翼運動過程分析可知，四旋翼運動狀態一般分為平移運動和轉動運動。因此，采用Newton-Euler 法對風場環境下的四旋翼的平移運動和轉動運動進行建模。

由空氣動力學可知四旋翼所受風場阻力為[15]：

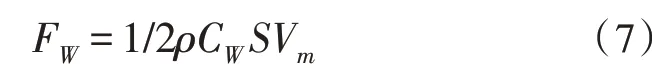
其中，CW為風場阻力系數，S為機身的有效面積，Vm為慣性坐標系下的風速大小。

因此，風場環境下四旋翼的平移運動和轉動運動方程為：

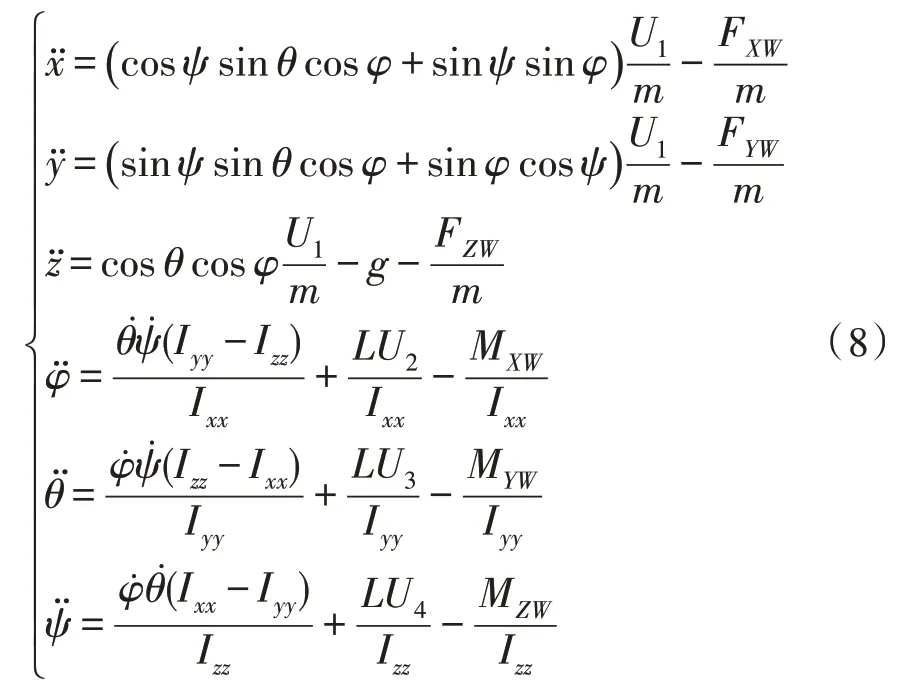
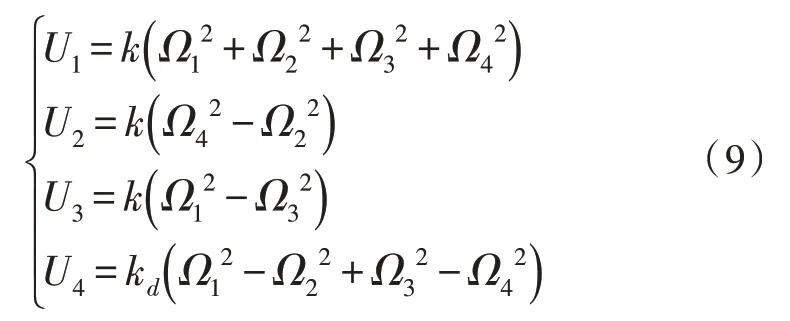
其中，k為升力系數，kd為阻力，Ω為電機轉速。

3 DAFEKF算法設計

在室外，由于風干擾因素的存在，要實現四旋翼的穩定飛行，就必須及時地獲取飛行器的位置和姿態信息。通過IMU 獲取的姿態數據具有大量噪聲，而EKF 濾波具有除去噪聲和對姿態進行實時估計的功能。但EKF 也存在缺陷，需要對其進行改進。

3.1 EKF算法

四旋翼飛行器的非線性系統[16]如式（10）：

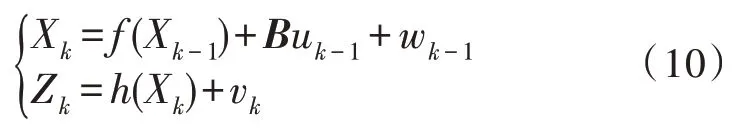
其中，Xk和Zk分別代表系統狀態量和觀測量；f(·) 和h(·) 代表非線性函數；B為控制輸入矩陣；wk-1和vk分別代表過程噪聲和測量噪聲。

根據EKF 理論可知，EKF 濾波算法[17]具體實現過程如下：

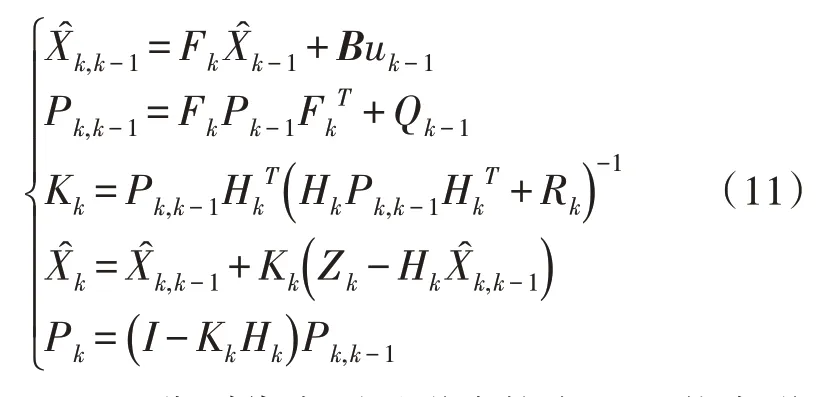
其中，R和Q分別代表測量噪聲協方差和狀態噪聲協方差。

在擴展卡爾曼濾波算法中，不僅存在目前濾波數據對歷史數據的過度依賴問題，而且R和Q通常為固定值。但是，四旋翼在室外飛行時，由于風場的影響，測量噪聲和狀態噪聲通常并不是固定值，這使得EKF 算法的濾波精度變低，抗風干擾能力變差。因此，設計了DAFEKF 算法。

3.2 DAFEKF算法

DAFEKF 算法不僅設計了自適應衰減因子，利用該因子來減小歷史數據對目前濾波數據的影響，同時，添加自適應因子來不斷對當前的Q和R進行調整，改善濾波精度，提高抗風干擾能力。

由EKF 理論可知，采用新息序列來描述實際測量值與預測測量值之間的誤差協方差[18]如式（12）：

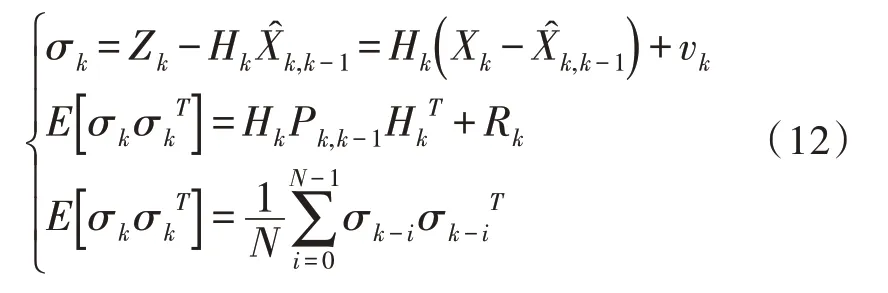
對R提取的自適應因子為：

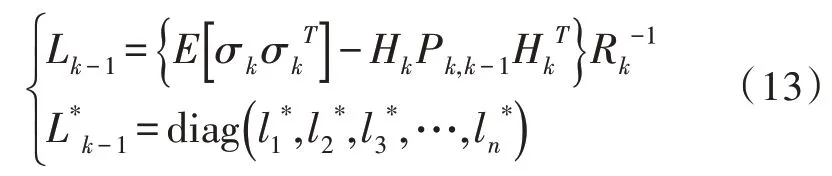
對Q提取的自適應因子為：

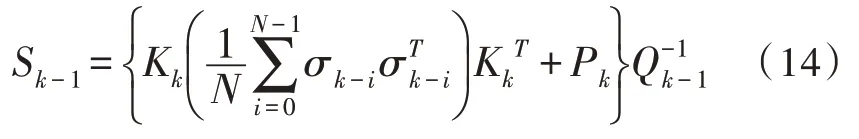
設計的自適應衰減因子λk如下：

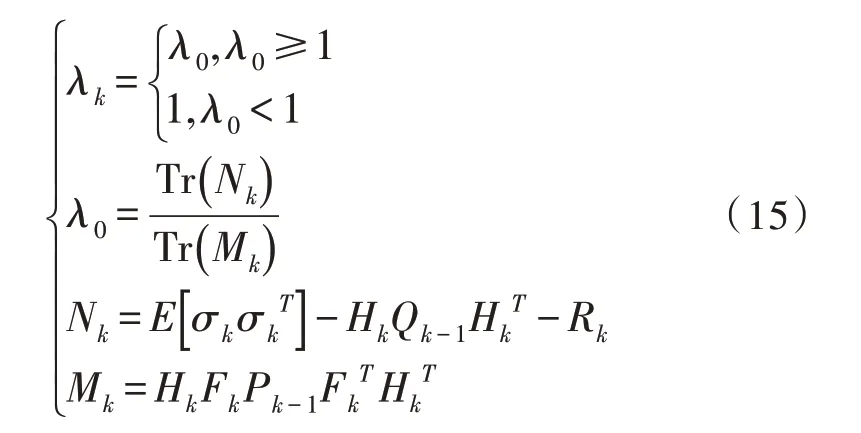
4 算法驗證與分析

該文分別對風場和風環境下的四旋翼動力學進行建模，設計了DAFEKF 濾波算法的狀態估計器，并與PID 控制器相結合。將建立的風場模型應用到四旋翼系統，通過MATLAB/Simulink 對整個系統進行建模。

設置四旋翼飛行器的初始位置X=[0 0 0]，期望位置X=[6 6 15]，初始姿態角η=[0 0 0]，期望姿態角η=[0 0 0.5]，風速為5 m/s。將新設計的帶有自適應因子的R和Q以及自適應衰減因子λk的PID-DAFEKF 控制系統與經典的R和Q為固定值的PID-EKF 控制系統，以及魯棒性強的滑模控制系統對風場環境中四旋翼實現定點懸停的控制效果進行對比。設置時間為30 s，對比結果如圖1 和圖2所示。

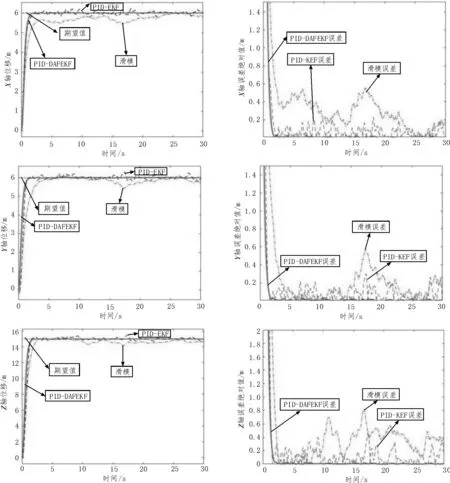
圖1 三軸位移輸出曲線和三軸位移絕對誤差值

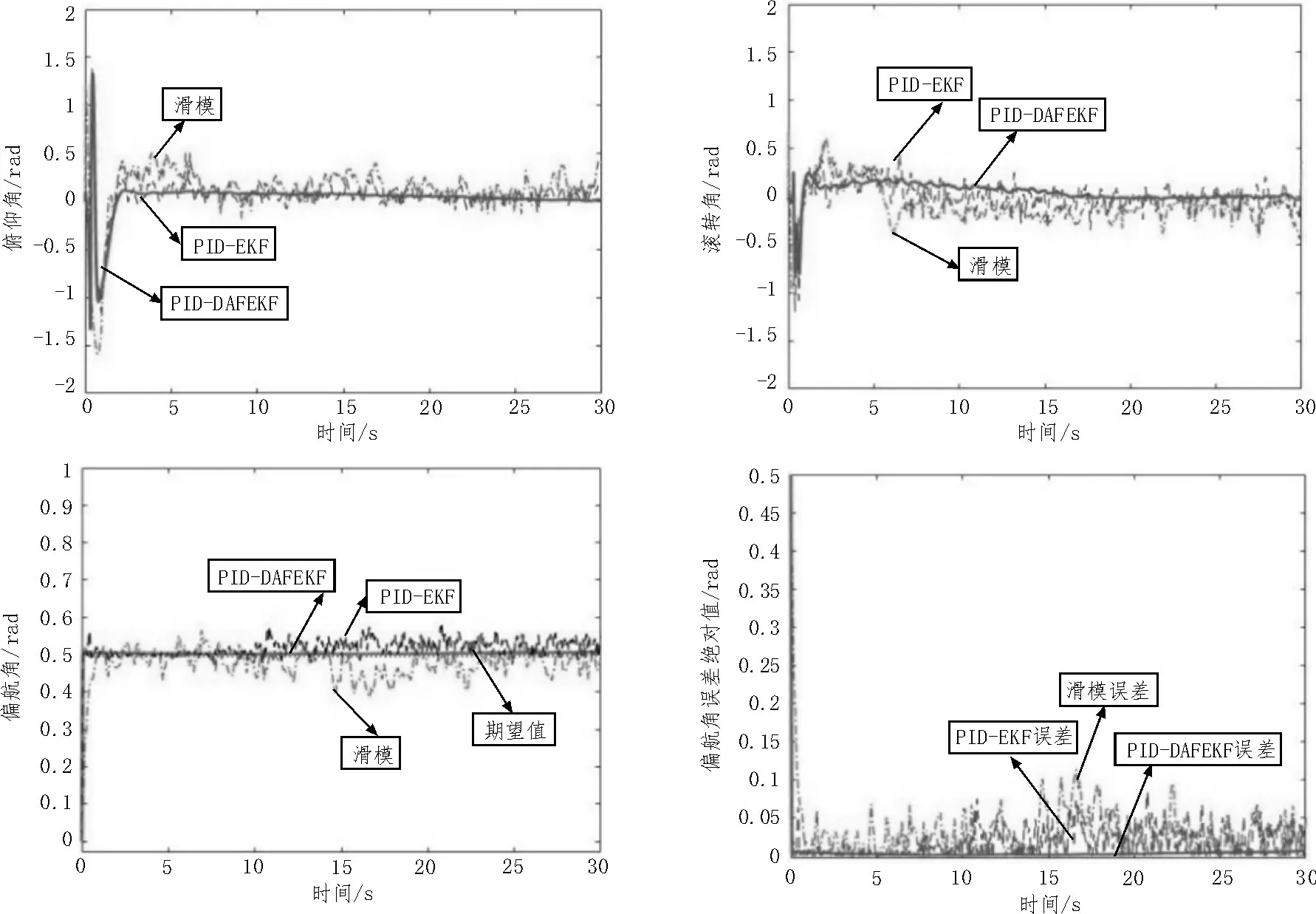
圖2 姿態角輸出曲線和偏航角誤差絕對值

由圖1 可知，在風場環境中，分別給四旋翼3 個方向設定期望值，并使用3 種不同的控制方式來實現四旋翼的定點懸停和抗風干擾控制。采用滑模控制算法后，三軸位移的最大絕對誤差分別約為0.58 m、0.59 m、0.81 m。雖然滑模有較強的魯棒性，但未對姿態數據進行估計。并且，由于風場的不斷擾動，使得滑模產生的抖動比較大，抗風干擾能力差。采用PID-EKF 算法后，不僅對飛行器姿態進行實時估計，還對姿態數據進行濾波處理，使得三軸位移的最大絕對誤差分別約為0.2 m、0.32 m、0.45 m。誤差相對減小，響應速度變快。采用PID-DAFEKF 算法后，對測量噪聲和狀態噪聲不斷在線更新，并引入自適應衰減因子，減少當前濾波值對陳舊數據的過渡依賴，使得三軸位移的最大絕對誤差分別約為0.05 m、0.06 m、0.06 m。提高了濾波精度，抗風干擾能力更強，使飛行器的懸停更加穩定，更加接近期望值。

由圖2 可知，在風場環境中，設定期望偏航角為0.5 rad。采用滑模控制算法后，X軸和Y軸方向上的位移抖動性比較大，使得俯仰角和滾轉角的波動比較大，飛行器穩定性差，同時，偏航角也產生了較大誤差，最大絕對誤差值約為0.12 rad。采用PID-EKF算法后，對飛行器的姿態進行估計，并對姿態數據進行了濾波處理，使得俯仰角和滾轉角的波動減小，也使得偏航角的誤差減小，最大誤差絕對值約為0.1 rad。最后，采用新設計的PID-DAFEKF 算法后，對測量噪聲和狀態噪聲不斷在線更新，并引入自適應衰減因子，使得姿態估計更加準確，濾波效果更好，偏航角的輸出更加接近期望值，最大絕對誤差幾乎為零。整體抗干擾能力好。位移與偏航角均方根誤差統計如表1 所示。

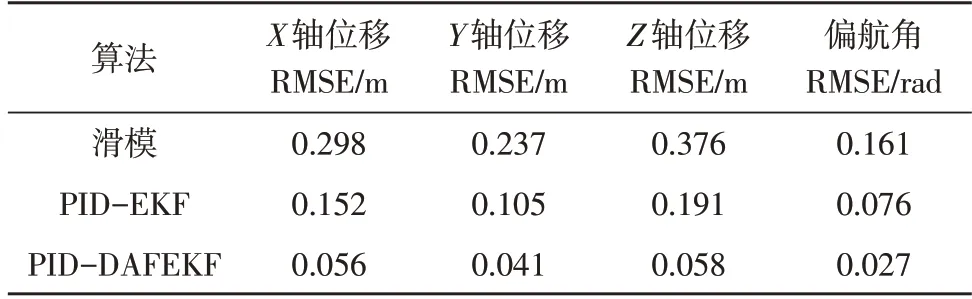
表1 位移與偏航角均方根誤差統計

由表1 可知，在風場環境下，采用滑模控制器后，位移與偏航角分別與期望值產生一定偏差。當使用PID-EKF 算法對飛行器姿態進行估計以及對姿態數據進行濾波后，使得RMSE 分別減少了49%、55.7%、49.2%、52.8%。通過新設計的PID-DAFEKF算法對EKF改進后，RMSE分別減少了81.2%、82.7%、84.6%、83.2%，其使飛行器的穩定性更好，抗風干擾能力更強。

5 平臺仿真

在前面使用MATLAB/Simulink 對新設計算法的可行性進行驗證，結果表明，該算法的抗風干擾效果好，為了進一步驗證該算法的合理性、有效性和可視化四旋翼飛行器在風場環境中的穩定性，一般采用飛行器實物進行抗風干擾實驗，但容易出現失控、墜機等現象，增加飛行器研究成本。因此，在開源仿真平臺建立3D 風場環境模型來實現四旋翼在仿真平臺的風環境中進行抗風干擾測試，代替使用四旋翼實物進行抗風干擾測試。實現四旋翼在風場中飛行姿態的可視化，降低飛行器研究成本。

5.1 3D風環境建模

該文采用Gazebo 三維動態仿真平臺，模擬復雜的室內外環境、機器人和飛行器。根據前面建立的風場數學模型，在Gazebo 仿真平臺的世界模型中建立風世界，將Gazebo 仿真平臺中的空世界轉變成風世界。并通過mavros 和mavlink 來實現Gazebo 仿真平臺與飛控平臺相連通。在Gazebo 仿真平臺模擬的風環境中，使用編寫的Ros 代碼對四旋翼進行目標位置設置，為X=[6 6 15]，并利用飛控平臺的外部控制模式來控制Gazebo 仿真平臺中的四旋翼，實現定點懸停。使四旋翼飛行器在風場環境中的穩定性和飛行姿態可視化。在風世界模型中分別對X軸和Y軸方向設置風速為5 m/s 的風場。定點懸停流程圖如圖3 所示，在X軸和Y軸風場環境下的姿態角如圖4 所示。

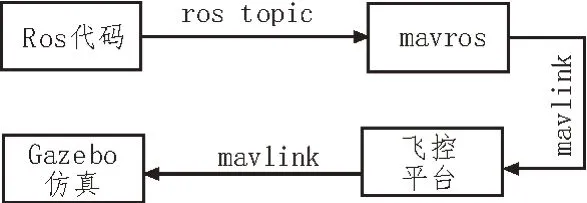
圖3 定點懸停流程圖

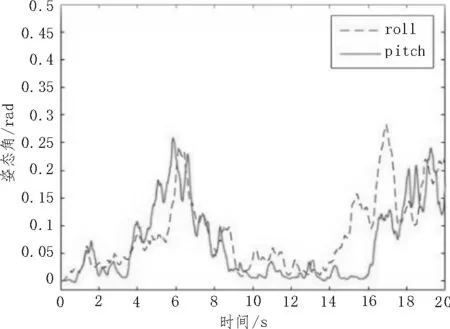
圖4 風場環境中的姿態角

圖3 流程圖顯示了通過Ros 代碼實現Gazebo 中的四旋翼的定點懸停控制。

由圖4 可知，在Gazebo 中首先引入沿X軸方向的風場，仿真平臺中的四旋翼在俯仰方向產生傾斜，并不斷抖動，俯仰角在0.15 rad 附近不斷變化。然后引入沿Y軸方向的風場，仿真平臺中的四旋翼在滾轉方向產生傾斜，并不斷抖動，滾轉角在0.17 rad 附近不斷變化。

5.2 軌跡跟蹤

完成Gazebo 仿真平臺中風世界的建立，并與飛控平臺相連通之后，通過QGC 地面站設置航點位置及航點任務，進行航跡規劃。在mission 模式下啟動四旋翼飛行器，使四旋翼飛行器在風場環境中進行軌跡跟蹤，結果如圖5 所示。

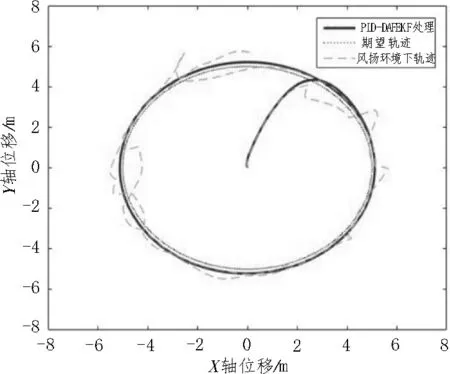
圖5 軌跡跟蹤

在Gazebo仿真平臺的風世界中，引入風速為5 m/s的風場，設置飛行高度為15 m，并啟動仿真平臺中的四旋翼在風場環境中進行航跡跟蹤。分析飛行器的飛行日志，由圖5 仿真結果可知，由于風場干擾，飛行器在3D 風場環境下的實際飛行軌跡與期望軌跡產生偏離。旋翼飛行器在俯仰方向和滾轉方向產生傾斜并不斷抖動；經過新設計的PID-DAFEKF 濾波算法處理后，在風場環境中，飛行器的實際飛行軌跡與期望飛行軌跡相吻合，軌跡跟蹤結果精確，四旋翼飛行器在風場環境中能穩定飛行，具有良好的抗風干擾能力和跟蹤效果。

6 結束語

根據四旋翼飛行器在室外飛行時所受的風場干擾，設計了PID 位置控制器與DAFEKF 濾波算法相結合的控制系統。在開源仿真平臺中建立3D 風場環境模型，實現通過仿真平臺中的風環境來驗證抗風干擾算法的有效性。實驗結果顯示，設計的控制系統不僅具有很好的抗風干擾能力，而且開源仿真平臺建立的3D 風場環境能很好模擬飛行器在室外飛行時所受到的風場干擾。