基于自適應網格劃分的針織物仿真

胡新榮，汪 卓，劉軍平，彭 濤，李 敏，李 麗

(武漢紡織大學, a.計算機與人工智能學院；b.紡織服裝智能化湖北省工程研究中心；c.湖北省服裝信息化工程技術研究中心,武漢 430200)

隨著計算機性能的不斷提升和計算機動畫以及服裝設計、虛擬現實等領域的發(fā)展，針織物的動態(tài)仿真成為了熱門的研究領域之一。針織物的動態(tài)仿真大多數采用物理模型，而物理模型采用動力學方程求解的形式能夠達到接近真實的仿真效果。物理模型的仿真方法又分為基于網格模型的仿真和基于紗線模型的仿真。

機織物一般由經紗與緯紗交錯編織構成，在仿真中，其節(jié)點結構可以看作網格，如圖1(a)所示，圖1(b)中展示了其網格模型。將紗線的交點作為其中網格的頂端，縱向和橫向的形變分別以縱向與橫向的彈簧表示，而斜向的形變使用對角線上的彈簧表示[1]。為了表示材料的彎曲，可以跨節(jié)點加入彎曲彈簧，故基于網格并使用彈簧質點模型的仿真方法能夠解決機織物的形變問題。而針織物一般由紗線的線圈按照一定的圖案編織而成，編織圖案的不同時，紗線在形成針腳時所體現的纏繞方式也各有區(qū)別。

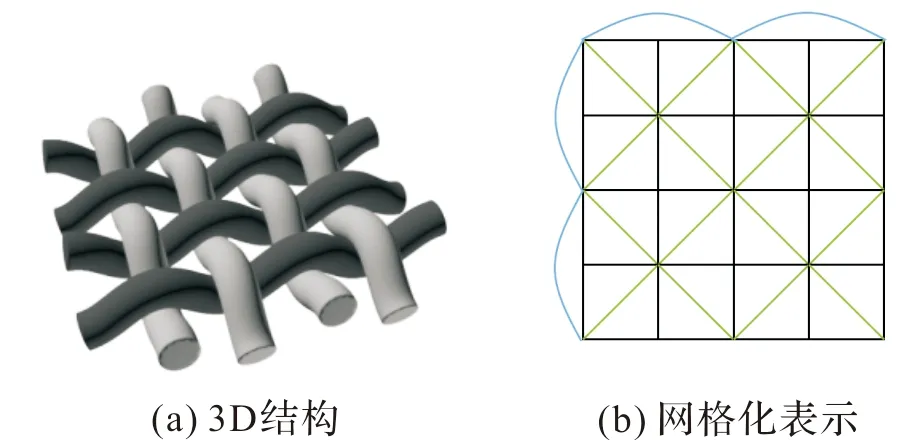
圖1 機織物模型及網格化表示

由于針法的不同，針織物在形變時所表現也不盡相同。比如彈力織物使用隔行正反針織法編織，而羅紋織物由一根紗線依次在正面和反面形成線圈縱行形成織物。這會導致彈力織物的邊緣會產生卷曲現象，而羅紋織物會產生收縮，并呈現周期性的條紋。圖2展示了彈力織物與羅紋織物編織的織物在靜止時所表現出的差異。與此同時，由于針織物的編織方式不同，同一針織物在受力方面可能會表現出各向異性，即不同方向的受力也可能產生不同的形變效果。

圖2 兩種編織方式織物的形變

如果使用傳統(tǒng)三角網格模型對圖2中的兩種針織物仿真，無法體現針織物紗線的編織信息，進而無法表征整個針織物在形變過程的物理特性。為了解決這個問題，一般的解決方法基于線圈模型，進行紗線級仿真。

線圈模型方面，傳統(tǒng)的Pierce線圈模型由圓弧表示的針編弧、沉降弧和直線表示的圈柱組成，該方法結構簡單卻無法展示真實的形態(tài)。現有的方法一般使用樣條曲線，并通過實際測量選取控制點。例如叢洪蓮等[2]測量了緯編提花織物的線圈結構，并選取控制點建立模型，而張華等[3]也通過類似的方法建立了經編織物的模型。徐海燕等[4]使用了TexGen軟件，采用了貝塞爾曲線插值的方法建立線圈模型，該方法建立的模型在曲線的表現與形態(tài)控制上更為方便。本文所使用的幾何模型由設定的控制點經樣條曲線插值而成。

針織物物理仿真研究中，Kaldor等[5]首次提出了紗線級別上進行針織物仿真的方法，但是由于碰撞檢測每一步都需要計算節(jié)點間的距離，該方法處理節(jié)點接觸的效率很低。隨后Kaldor等[6]使用線性化接觸模型與分塊計算的方法簡化了碰撞檢測中的接觸力計算過程，提高了整體仿真的效率。Yuksel等[7]提出了針織網格的數據結構，并以此為依據對織物進行仿真；該方法為自動化編織與交互式織物設計打下基礎。Cirio等[8-9]為了提升效率，假設針腳間持續(xù)接觸，避免了接觸節(jié)點間的碰撞檢測，在不損失精度的同時提升了仿真的效率。Jiang等[10]在Cirio的工作的基礎上，引入物質點法，使仿真效果更加真實。Fei等[11]在該方法的基礎上研究了基于紗線模型的織物與水接觸所產生的形變特征。

紗線級織物仿真，首先將紗線模型進行離散化處理，在每個針腳處形成接觸節(jié)點與紗線之間的彈力模型。圖3(a)、圖3(b)是對一個簡單的針腳離散化的紗線模型。在圖3(b)中，互相纏繞的紗線被簡化為直線，而接觸處的圓圈表示接觸節(jié)點。對于更復雜的針腳，如加針，其離散化表示也更為復雜，如圖3(c)、圖3(d)所示。對這些接觸節(jié)點進行受力分析，列出關于能量的方程為紗線級仿真常用的求解形式。由于機織物也由紗線紡織而成，該方法的紗線模型經過改動后一般也可以用于機織物的仿真。紗線仿真雖然能真實地表現針織物的變形特征，但是由于建模的復雜性，在模型節(jié)點較多，或分辨率較高時，其仿真速度一般都很慢。

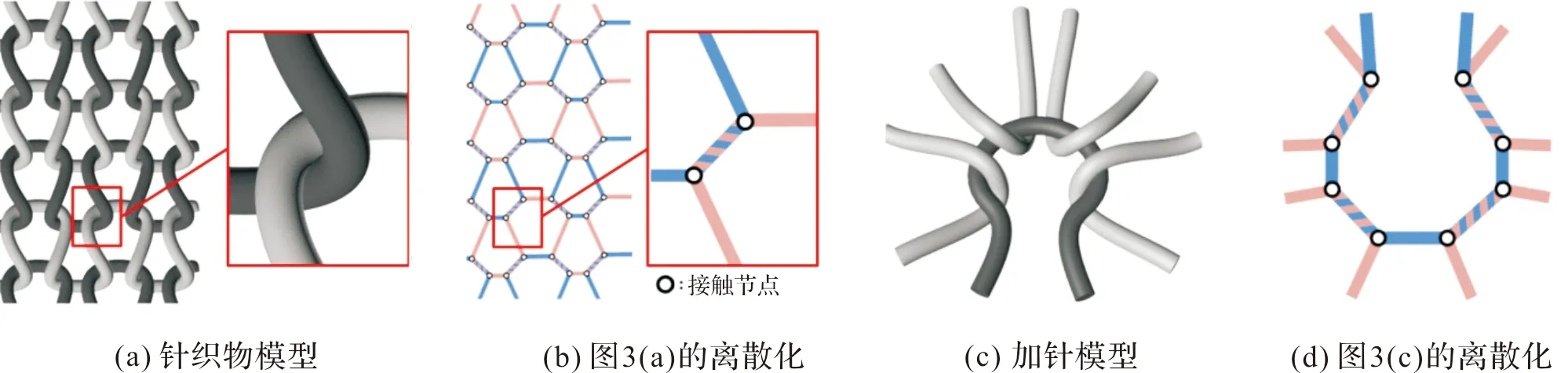
圖3 針織物的3d模型及離散化表示

另一些研究使用混合網格與紗線的模型進行織物的仿真。Narain等[12]提出了在動態(tài)網格劃分技術在織物仿真上的應用，Casafranca等[13]將兩種仿真方法混合使用，在變形較明顯處使用紗線仿真，其他地方使用網格仿真并引入平滑因子消除兩者結果之間的誤差，但紗線仿真區(qū)域需要在仿真前手動指定。Leaf等[14]以織物圖案的周期性對仿真進行探討。Sperl等[15-16]提出了均質化紗線仿真的方法，該方法在微觀層面使用周期性的紗線模型進行紗線級別的仿真，用來度量不同形變下該紗線模型的形變特征，將其結果映射到網格仿真的宏觀織物模型上，得到最終的結果。李雙雙等[17]提出自適應網格的方法進行織物仿真，使用到了邊緣曲率檢測的方法，但該方法的劃分依據完全依靠幾何信息，對真實的物理形變不夠敏感，且不適用于針織物。

綜上所述，目前的針織物仿真技術由于建模復雜，其仿真效果比起網格模型而言，更加接近物理真實，但由于其方程求解過程復雜，仿真過程非常慢，難以在短時間內得到一個比較準確的效果。

由于針織物大多數都使用某種特定的圖案進行編織，只對周期性的圖案進行仿真，避免重復計算加快針織物的仿真速度，而該特性同樣可以結合傳統(tǒng)的網格仿真方法。同時，引入自適應網格劃分技術可以提高網格仿真的效率。結合以上幾種技術的特性，本文將提出一種基于自適應網格的針織物仿真方法。

1 網格化與動態(tài)劃分

在織物形變過程中，有些接觸面比較平整，使其形變幅度較小；而有些接觸面比較窄，或者凹凸不平，容易產生較大的形變。為了在分辨率較低的初始網格模型在形變細節(jié)上也能得到較好的仿真效果，以及提高仿真的效率，將采用自適應網格劃分技術，同時為了結合紗線仿真，將對于針織物模型做一些特別處理，其中形變表示方法與約束參考Narain等[12]的論述。

1.1 網格表示

如圖4所示，將初始服裝網格的UV坐標為基礎，生成背景網格。和服裝網格模型不同，周期性紗線圖案一般為正方形，如圖4(a)，所以背景網格也是正方形，網格尺寸為周期圖案的尺寸。圖4(a)所示的網格大小為1×1，圖4(b)的服裝模型的腰寬為5，網格密度為6.25。然后用周期性的紗線圖案去鋪滿整個背景網格，隨后去掉服裝網格之外的頂點與紗線段，即可生成初始的紗線模型與網格的對應關系。

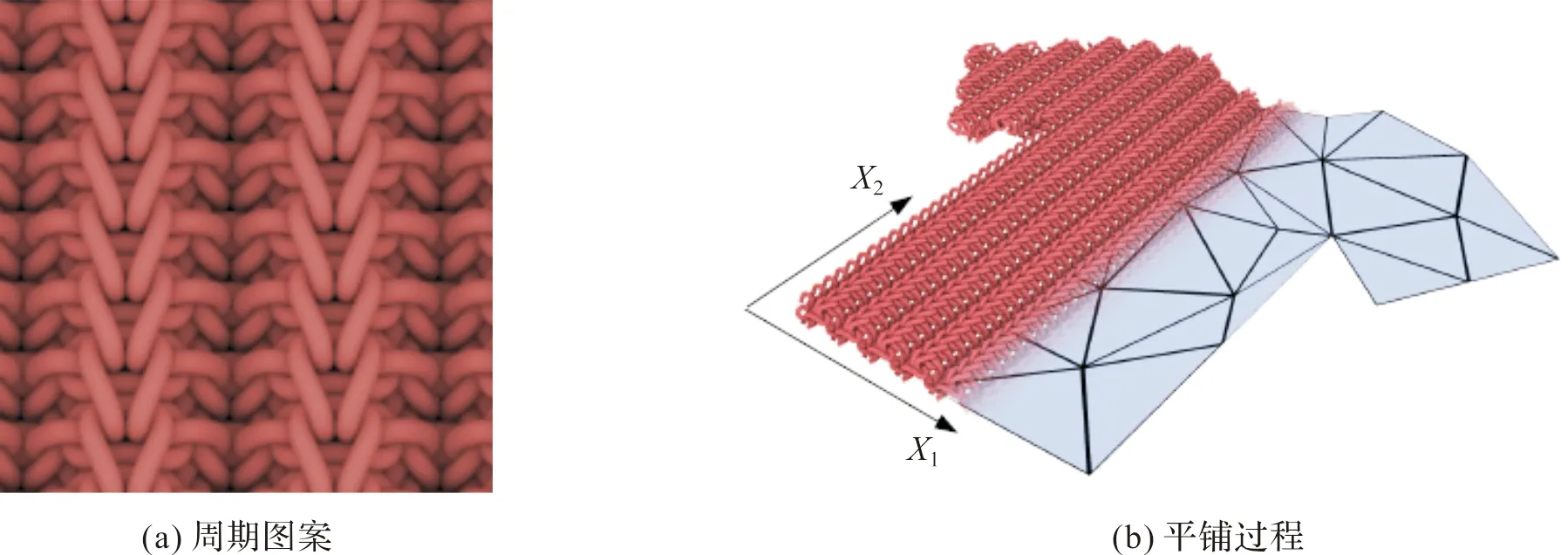
圖4 建立初始網格與紗線圖案對應關系[16]

為了得到不同尺寸的服裝紗線模型，網格密度可以結合實際需求進行調整。在后續(xù)實驗中，將統(tǒng)一使用圖4所示的網格密度與尺寸。

在初始模型生成后，每個三角網格與其范圍內的紗線一一對應，網格在后續(xù)映射步驟中對應的是紗線模型的中位面，中位面頂點的位置決定形變的宏觀效果，而其網格對應的紗線片段的形變決定其形變的細節(jié)。圖5是周期性紗線模型與其對應三角網格在形變中經歷的變換過程。自適應劃分后，其網格切分與組合也會使其對應的紗線模型片段切分或組合。

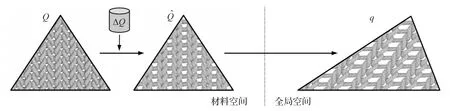
圖5 網格到紗線模型映射過程[15]

1.2 形變描述

本節(jié)將描述網格模型與紗線模型上，形變的表示方法。

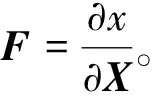
宏觀量與微觀量之間的對應關系如下：

(1)

(2)

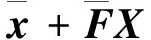
(3)

其對應的關系如圖6所示。

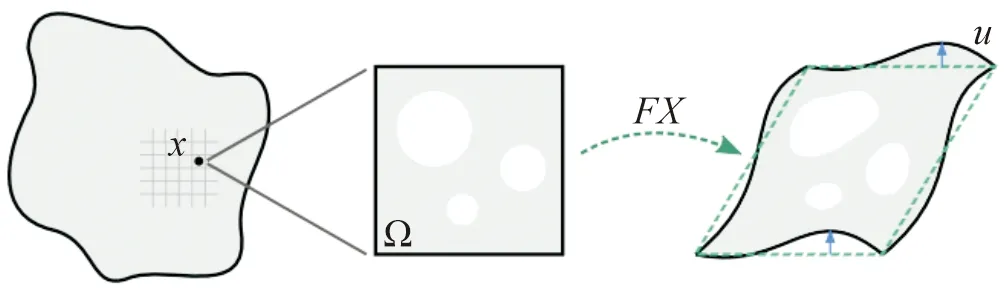
圖6 網格形變描述

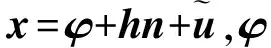
1.3 周期約束

區(qū)別于普通的網格仿真，為了整體模型紗線的連貫性，周期性的紗線模型在映射到網格后，必須要加上紗線的周期性約束。在視覺效果上，相鄰兩個網格之間所對應的紗線頭不能隨意斷開，也不能出現不連貫的彎曲。

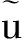
(4)

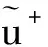
(5)

同樣地，該式也可記作：

(6)

式中：R為旋轉矩陣，由于旋轉矩陣是正交矩陣，所以R-1=RT。為了使紗線扭曲符合周期性約束，約束區(qū)域Ω內正反向扭曲相抵，即θ+=θ-。這些約束條件會在進行物理仿真時減少其過程中產生的計算誤差。

1.4 自適應劃分

由于仿真過程的總體形變效果是由網格模型產生的，在建立網格與紗線模型的對應關系后，需要對網格模型進行仿真。為了提高仿真的效率，并保持網格模型處理整體形變時的準確性，在仿真過程的每一次迭代之后，需要根據形變的大小、速度、碰撞點的距離等參數進行自適應網格劃分。

總體而言，自適應劃分的操作對象是網格模型的邊，以上一步所得到的網格模型為基礎，首先需要對網格進行細分，為了保證網格邊緣與形變特征，都需要對網格邊進行翻轉。為了防止網格的無限細分，然后網格然后進行粗化。網格粗化后也要對部分邊進行翻轉操作。根據Narain等[12]的論述，為了準確地細分網格，首先需要計算張量場M，該場代表了網格中每條邊被允許的最大長度。當一條邊的s>1時，需要對該邊進行切分。記Xij=Xi-Xj，則兩個頂點i和j的距離s與M之間的關系可以定義為式：

(7)

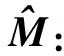
(8)

(9)

(10)

(11)

(12)

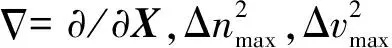
(13)

(14)

(15)

然后令Λ=diag(λ1,λ2)，最后得到M=QΛQT。

如圖7所示，對邊AC進行切分是加入AC的中點P，由于AC被三角形ABC和ACD公用，所以需要連接PB和PD。同時將速度、張量場M等參數插值給點P。對AC進行翻轉操作則是去掉AC連接BD。粗化AC則是去掉點A，并將原來與A連接的邊改為與C連接。粗化過程中邊是有向的，也就是說粗化CA是去掉點C再將與A相連的邊連向C。

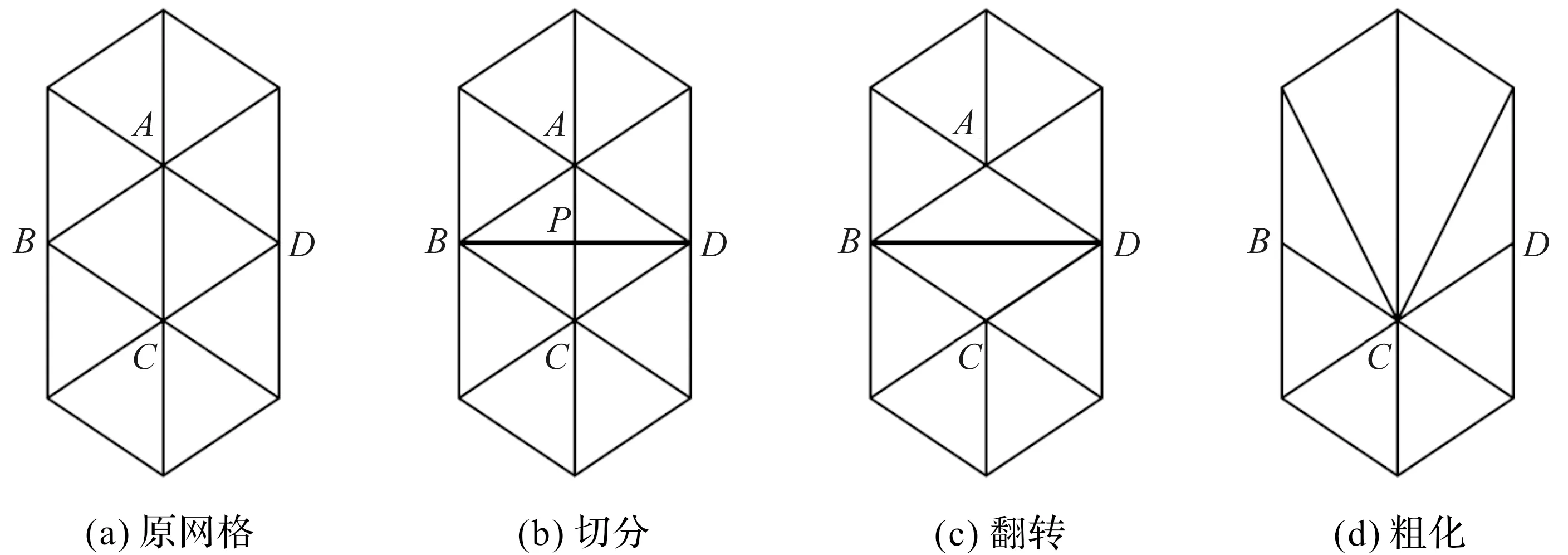
圖7 對邊AC網格劃分操作

當邊AB去掉點A引入的新邊不需要重新劃分，且去掉該點不會影響網格UV圖的外形時，可以對AB進行粗化操作。當一條邊AC的τ<1時需要將該邊翻轉至BD。其中τ定義為式：

(16)

整個自適應劃分的流程如圖8所示。

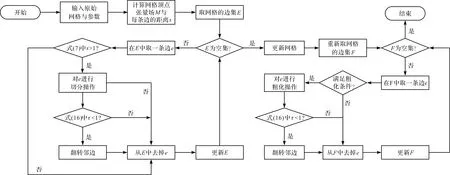
圖8 自適應網格劃分流程

2 物理仿真

仿真的流程如圖9所示。下文將分別介紹其中的細節(jié)。

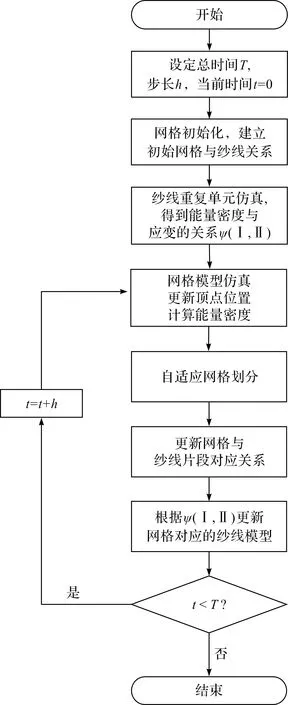
圖9 針織物仿真流程

2.1 紗線仿真流程

由于直接對整個紗線模型進行紗線仿真很慢，對需要進行仿真的材料，文中只對其周期性的重復單元進行紗線仿真。周期性模型輸入包含了紗線材料的參數，以及編織紗線的節(jié)點坐標，使用三階B樣條曲線插值可以得到該周期模型的圖案。

紗線仿真所使用的模型是Bergou等[18]提出的離散彈性繩結模型。在仿真過程中，為了更加真實地體現出紗線模型邊緣的形變，需要通過周期模型的一小部分，經過平移、旋轉操作在其邊緣稍做擴展。

接著分析紗線的能量：

(17)

式中：Es為紗線的拉伸能量，Eb為彎曲能量，Et為扭曲能量，Ec為每個周期模型間的碰撞能。能量對坐標x求導，就可以得到紗線的受力情況。

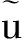
(18)

式中：|Γ|為中位面Ω的面積。

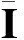
(19)

2.2 網格仿真流程

對于織物的宏觀形變可以使用基于三角網格的仿真來解決。這種仿真使用彈簧質點模型，首先對該模型進行受力分析，確定求解的微分方程，然后選取合適的時間步長進行求解。

求解物理仿真求解微分方程的方式可以分為顯式時間積分與隱式時間積分。顯式時間積分法一般采用較小的時間步長，否則容易產生數值波動，使得視覺上會出現抖動等現象，但時間步長小的仿真效率很低。所以織物仿真一般使用隱式時間積分[20]。其優(yōu)勢在于可以配合更大的時間步長，并且可以在求解過程中獲得更穩(wěn)定的物理仿真效果，劣勢則是增加了求解步驟中的復雜性。

求解微分方程前，首先計算每個網格三角形面片的形變梯度FΔ，公式如下[14]：

(20)

式中：φi與ξi表示材料空間和全局空間下，網格中第i個頂點的坐標。

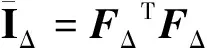
(21)

式中：θi為網格與第i個相鄰網格平面之間的夾角，A為三角網格面片的面積，li為第i條邊的邊長，ti是長為li的三角網格面的法向量。

2.3 紗線模型生成

在自適應劃分之后，整個網格發(fā)生了變化，但紗線模型只是跟著網格模型發(fā)生形變，此時，需要重新建立網格與紗線片段的對應關系。通過網格邊切割紗線模型的辦法即可做到。

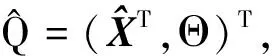
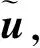
最終得到整體形變后的紗線模型。

對于網格仿真后輸出的網格模型，采用上述方法即可得到對應的紗線模型。

3 實驗結果

本實驗代碼使用C++語言以及OpenGL框架編寫，運行于Intel Corei7-9700八核處理器、NvidiaGTX 1060 6GB顯卡與Ubuntu 20.04操作系統(tǒng)上。下面將從織物的懸垂效果與著裝兩個實驗來分析使用自適應網格仿真的效果。

3.1 懸垂實驗

為了表現不同織物形變的特點，實驗使用了彈力織物、羅紋織物與席紋織物3種不同的織物模型作為輸入，分別觀察它們在與球碰撞后的懸垂效果，仿真過程中織物的兩個頂點與球的位置是固定的。實驗使用的初始網格模型含有2625個頂點，5168個網格，總體的仿真時長為2 s，每幀的時間步長為1/60 s，但仿真在0.5 s時，整體開始趨于收斂。

圖10是仿真進行至t=0.5 s時，彈力織物、羅紋織物和席紋織物分別在橫列與縱列與球碰撞產生的形變效果。在彈力織物與羅紋織物中，兩種懸垂方式的形變效果差異較大，而席紋織物由于其橫列與縱列的針法相同，其懸垂效果無明顯區(qū)別。而同一懸垂方向下，3種不同的織物也顯示出了各自不同的形變效果。

圖10 t=0.5 s時不同編織方式下懸垂效果

圖11顯示了羅紋織物橫向懸垂在實驗的仿真過程中在3個不同時刻網格劃分情況。可以看出在形變過程中固定點和碰撞部分及中間部分網格進行了細分。

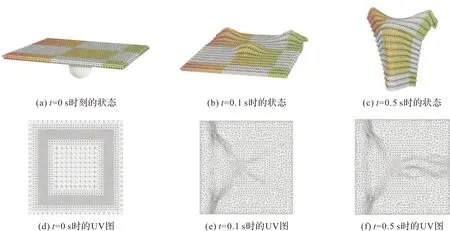
圖11 自適應網格劃分效果

3.2 著裝實驗

為了計算使用自適應網格劃分仿真的時間效率提升幅度，以及觀察低分辨率網格模型輸入下的形變效果，實驗對于5種不同的針織模型結合人體動畫進行服裝仿真，原始服裝網格使用了3303個頂點與6514個網格。表1為幾種材料的參數。

表1 實驗用紗線圖案的參數

預設動畫的時長為20 s，時間步長為1/60 s，即動畫總共有1200幀，該動畫只包含人體模型的運動過程。而仿真過程中，需要逐幀計算服裝模型的形變以及與人體之間的碰撞，通過迭代使得某一幀的服裝模型穩(wěn)定后，將該幀的服裝模型和下一幀的人體模型輸入，再進行下一幀的仿真過程，直到動畫對應的仿真過程全部結束，整個仿真過程完成。動畫每一幀的形變計算所耗費的時間總和即仿真的總時長。最后，將使用自適應劃分仿真所減少的耗時與使用原始網格的仿真耗時相除，得到時間效率提升的百分比。

實驗結果表明，由于仿真過程與模型的頂點數相關，且自適應劃分方法相比原始網格減少了20%～30%的頂點與網格數，在仿真計算過程中減少了計算量，使得使自適應網格劃分比起直接使用原始網格在時間效率上有23%～40%左右的提升，其最大提升為39.7%，結果見表2。其中羅紋織物比起其他針法，由于收斂較慢使用了2倍左右的仿真時間。

表2 仿真結果對比

形變效果如圖12所示。使用動態(tài)網格化劃分與使用原始網格的實驗效果對比。在第300幀下，使用動態(tài)網格劃分的方法效果如圖12(a)所示，而使用原始網格的情況下效果如圖12(b)所示。可以看出圖12(a)相比圖12(b)在較大形變展現出了更加接近真實的效果，而圖12(b)由于其網格過于稀疏，其仿真效果比較圖12(a)產生了過多的褶皺。

為了得到兩個模型間的形變差異分布，實驗計算兩個網格頂點之間的Hausdorff距離[22]，即找到圖12(b)中每個頂點在圖12(a)中最近的頂點及其距離，最后將該距離映射到圖12(a)的網格上，其熱力圖如圖12(c)所示。圖中顏色越深代表其形變差異越大。可以看到在形變較大的位置，如圖12(c)用虛線框圈出的位置存在明顯差異。

圖12 使用自適應網格與原始網格的效果對比

4 結 論

由于虛擬現實及動畫制作、針織自動化生產等一系列日益增長的需求，針織物仿真成為了計算機物理仿真的研究重點。為了解決針織物仿真使用傳統(tǒng)網格模型細節(jié)效果不夠真實以及紗線模型仿真建模復雜導致仿真效率低下的問題，本文提出了一種結合自適應網格與紗線仿真的針織物仿真方法，在使用網格模型進行宏觀效果的仿真的同時使用紗線最小重復單元在不同形變下的映射來改進微觀效果，該方法體現不同的針織物在形變細節(jié)上的特點，并且在時間效率上得到了時間效率上23%～40%的提升。但該方法的紗線模型在設計上只能針對周期性紗線編織的織物，沒有考慮非周期性的或者多個重復單元的模型，故不能直接使用此方法表示與仿真更加復雜的織物模型。