基于模糊擬合圖像驅動的苗族服飾圖像分割算法

馮 潤，黃成泉，胡 雪，周麗華，鄭 蘭

(貴州民族大學，a.數據科學與信息工程學院；b.工程技術人才實踐訓練中心；c.民族醫藥學院，貴陽 550025)

圖像分割作為圖像處理與計算機視覺領域中一個重要的階段[1]，主要是將圖像分成若干個不相交的區域，然后提取出感興趣特征的一項關鍵技術。而主動輪廓模型作為圖像分割的重要方法之一，由于其具有靈活選擇約束力和作用域、統一開放式的描述形式等優勢，在圖像分割領域中得到了廣泛的應用。目前，已有的主動輪廓模型圖像分割算法的優化中，主要針對合成圖像和醫學圖像分割等主流應用，針對少數民族服飾圖像分割算法與優化的研究案例較少。其中，部分是基于C均值模糊聚類[2]、基于塊匹配的協同優化方法[3]與基于閾值分割法[4]的少數民族服飾研究，基于主動輪廓模型[5]的少數民族服飾圖像分割的研究較少。

在過去的研究中，人們提出了許多經典的主動輪廓模型，主要分為基于邊緣的模型和基于區域的模型。在基于區域的模型中，Chan-Vese(CV)模型[6]作為最經典的模型之一，假設待處理圖像具有均勻的強度，并且可以根據強度特征劃分為幾個不相交的子區域，從而達到對均勻圖像進行有效的分割。但是，該模型不能很好的處理強度不均勻的圖像。隨后，眾多學者提出了許多基于區域的模型，例如：基于圖像局部信息的局部二值擬合(Local binary fitting, LBF)模型[7]、基于局部圖像擬合(Local image fitting, LIF)模型[8]、基于模糊能量的主動輪廓(Fuzzy energy-based active contour, FEAC)模型[9]以及基于混合與局部模糊區域邊緣的主動輪廓分割(Region-edge-based active contours driven by hybrid and local fuzzy region-based energy, HLFRA)模型[10]等，這些模型都能夠很好的處理具有強度不均勻的自然、合成與醫學圖像。如前所述，雖然基于區域的主動輪廓圖像分割算法在自然、醫學與合成等圖像的分割上取得了非常豐碩的研究成果，但對少數民族服飾圖像進行分割的研究較少。如劉其思等[11]采用變分水平集算法對服飾圖案輪廓進行邊緣檢測和分割，結果表明，基于變分水平集算法相較于傳統的分割方法更為準確有效，但是使用變分水平集算法難以滿足復雜圖案分割的需求。侯小剛等[5]通過融合形態學連通域標記和CV模型，提出了一種民族服飾圖案紋樣元素分割的方法。該方法與其他自動分割算法相比更為有效，但是想要在較高邊界召回率的情況下實現較高的分割準確率還存在一定差距。

綜上所述，與主動輪廓模型在處理自然、醫學與合成圖像等主流圖像相比，苗族服飾圖像作為一種特殊的圖像類型，具有繡線紋理、種類繁多、形狀復雜度高、色彩差異大以及服飾圖像的不善保存導致獲取的圖像存在破損與不清晰等問題，采用現有的主動輪廓模型圖像分割技術對苗族服飾圖像進行分割并未取得較好的分割結果。同時，由于基于全局的主動輪廓模型不能很好的分割灰度不均勻的圖像，基于局部的主動輪廓模型存在對初始位置敏感以及容易陷入局部極小值等問題。因此，以主動輪廓模型為基礎的苗族服飾圖像分割面臨著極大的挑戰。針對這些問題，本文在HLFRA模型[10]的啟發下，提出了一種基于模糊擬合圖像驅動的苗族服飾圖像分割算法，在一定程度上對少數民族服飾圖像分割算法的研究提供參考。

1 相關模型

1.1 FEAC模型

針對基于全局的主動輪廓模型缺乏分割亮度不均勻圖像的能力以及基于局部的主動輪廓模型對初始輪廓的位置敏感與容易收斂到局部最小值等問題，Lv等[12]提出了一種基于分數階擴散邊緣指標和模糊局部擬合圖像的模糊主動輪廓模型。模糊能量函數表示為：

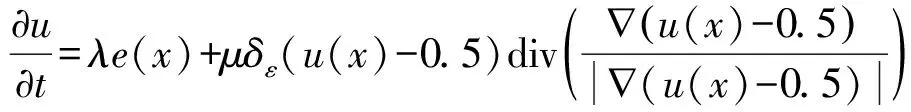
+vspfL(I(x))δε(u(x)-0.5)+γspfG(I(x))

(1)

式中：λ、μ、ν和γ為正常數，div(·)為散度運算符，u(x)為偽水平集函數，e(x)表示局部模糊能量項，spfG(I(x))和spfL(I(x))分別表示全局和局部符號壓力函數，定義為：

e(x)=(m1(x)-m2(x))

(2)

(3)

spfL(I(x))=

(4)

式中：IFLFI(x)=u1(x)m1(x)+u2(x)m2(x)表示模糊局部擬合圖像，W(x)=1/(1+exp(-M(x)))用于縮放I和IFLFI之間的Kulback-Leibler散度，c1、c2、m1(x)和m2(x)分別表示全局和局部內外強度平均值。

FEAC模型具有靈活的初始化方法，并且能很好的解決具有弱邊界的圖像以及容易陷入局部最小值等問題。同時，該模型在分割具有亮度不均勻的合成圖像和真實圖像方面能得到令人滿意的結果。但是，當存在大部分目標對象與背景區域非常相似的情況時，該模型不能很好地進行分割。

1.2 HLFRA模型

為了分割具有高噪聲和強度不均勻的圖像，Fang等[10]在FEAC模型[9]的基礎上提出了一種基于混合和局部模糊能量的區域邊緣主動輪廓模型。該模型的能量函數由區域能量和邊緣能量兩部分組成，區域能量激勵初始偽水平集函數向目標邊界移動，邊緣能量用于精確檢測目標邊界。能量函數定義為：

F(u)=FR(u)+FE(u)

(5)

其中，FR(u)表示區域能量，FE(u)表示邊緣能量，分別定義為：

(6)

FE(u)=β1L(u-0.5)+β2P(u-0.5)

(7)

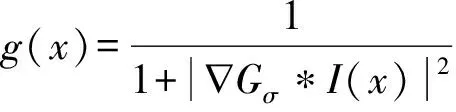
通過固定fb、fs、c1和c2，公式(6)相對u(x)最小化，得到隸屬度函數為：

u(x)=

(8)

然后根據區域能量ΔF的變化來更新隸屬度函數u(x)。

在HLFRA模型中，區域能量能夠引導演化曲線向目標邊界運動，邊緣能量使演化曲線精確地停在物體邊界上，該模型還通過計算新舊能量函數的差值來更新偽水平集函數。實驗結果表明，HLFRA模型能夠有效地從高噪聲和強度不均勻的合成和真實圖像中提取目標，且凸區域能量保證了分割結果與初始條件無關。

2 本文算法

2.1 能量函數構造

在上述模型的啟發下，本文提出了一種新的基于模糊擬合圖像驅動的苗族服飾圖像分割算法。使用0.5水平集作為演化曲線[9,10,12]，將圖像域Ω分成內部Cin(u>0.5)和外部Cout(u<0.5)兩個相鄰區域。由于全局圖像信息能夠處理灰度均勻的圖像，局部圖像信息在灰度不均勻方面起著重要作用。因此，結合全局與局部圖像信息在模糊區域中擬合出模糊局部與全局圖像，并將原始圖像和擬合的模糊局部與全局圖像在Kullback-Leibler散度方面的圖像差異構造模糊能量函數。然后通過圖像局部與全局內外區域的像素灰度歸一化類內方差構造自適應權重系數。接下來，添加了一個正則項與一個長度項，并在其中引入一個邊緣檢測器。最后，通過標準梯度下降法[13]最小化能量函數，并給出了算法的具體步驟。所提出的能量函數定義為：

E(u)=Ffe(u)+Fedge(u)

(9)

式中：Ffe(u)是模糊能量函數，Fedge(u)由正則項與長度項組成。

2.1.1 模糊能量函數

模糊能量函數由局部與全局模糊能量項組成。不同于HLFRA模型中混合局部模糊能量，本文在其基礎上，擬合出模糊局部與全局圖像。并依據FEAC模型通過Kullback-Leibler散度來量化原始圖像與擬合圖像之間差異的方法，通過原始圖像與兩幅模糊擬合圖像在Kullback-Leibler散度方面的圖像差異構造局部與全局模糊能量項。同時，通過自適應權重系數來自動調節局部與全局模糊能量項之間的參數。模糊能量函數定義為：

(10)

式中：第一項是全局模糊能量項，能對灰度均勻的圖像進行分割。第二項是局部模糊能量項，分割灰度不均勻的圖像。wg和wl為兩個權重系數，滿足wg+wl=1。ILFR(x)與IGFR(x)表示模糊局部與全局擬合圖像，分別定義為：

IGFR=c1[u(x)]m+c2[1-u(x)]m

(11)

ILFR=m1[u(x)]m+m2[1-u(x)]m

(12)

這里IGFR與ILFR可以認為是原始圖像I在全局與局部窗口內的模糊逼近，c1和c2為全局強度平均值，m1和m2為局部強度平均值，u(x)表示模糊隸屬度函數，分別定義為：

(13)

(14)

u(x)=

(15)

式中：[u1(x)]m=[u(x)]m、[u2(x)]m=[1-u(x)]m，m為每個模糊隸屬度的加權指數，w(x,y)為空間權重，α1、α2、β1和β2為正加權參數。

在式(10)中，為了根據圖像的均勻程度來自動調整全局與局部模糊能量項之間的參數，從而構建了一個自適應權重系數。不同于Jiang等[14]和Han等[15]基于全局圖像輪廓曲線內外區域的像素灰度歸一化類內方差來定義權重系數，本文在此基礎上結合了局部圖像輪廓曲線內外區域的像素灰度歸一化類內方差來表示：

(16)

式中：a1、a2分別表示圖像全局輪廓曲線內外區域像素灰度的類內方差，b1和b2分別表示圖像局部輪廓曲線內外區域像素灰度的類內方差，分別定義為：

(18)

式中N表示整個圖像區域的像素數。

2.1.2 正則項與長度項

在式(9)中，將邊緣檢測器g分別引入正則項與長度項，以此來獲得光滑的輪廓曲線，平滑圖像邊緣。分別表示為：

Fedge(u)=μLg(u=0.5)+νPg(u=0.5)

(19)

這里，μ、ν為常數，Lg(u=0.5)表示水平集函數的長度項，Pg(u=0.5)表示符號距離函數的正則項，定義為：

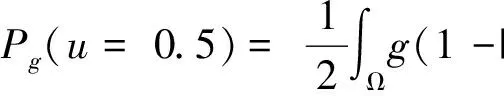
2.2 能量函數求解

本文通過標準梯度下降法最小化式(9)中的能量函數，對于固定的c1、c2、m1和m2，E(u)相對于u(x)最小化：

(22)

這里e1和e2分別為：

(23)

(24)

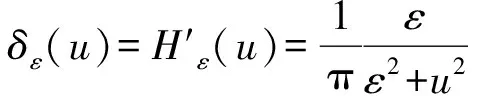
2.3 算法步驟描述

本文算法的具體計算步驟為：

a)輸入指定的圖像，并輸入初始參數：即迭代次數IterNum、局部窗口(2k+1)×(2k+1)的大小k、常數ε、時間步長Δt、權重μ、ν、α1、α2、β1、β2和邊緣檢測器g；

b)初始化水平集，將其設置為u0(x)>0.5與u0(x)<0.5兩個部分；

c)使用式(15)計算u(x)的偽水平集函數，并使用式(13)計算兩個全局變量平均值c1和c2以及式(14)計算兩個局部變量平均值m1和m2；

d)通過式(11)、(12)、(23)、(24)、(10)分別計算IGFR、ILFR、e1、e2和模糊能量函數Ffe(u)，并通過式(16)計算權值wg和wl；

e)對于正則項Pg和長度項Lg分別使用公式(21)、(20)進行計算；

f)結合式(9)，更新能量函數；

g)重復步驟c)-f)，直到迭代完成。

3 實驗結果與分析

為了驗證本文算法的有效性，本節設計4組實驗進行分析，即自然圖像分割比較分析、苗族服飾圖像的分割、苗族服飾圖像分割比較分析、不同初始形狀與位置的苗族服飾圖像分割。依據自然圖像與苗族服飾圖像之間的圖像性質以及圖像的獲取方式等關聯，特別是具有紋理的自然圖像與苗族服飾圖像有異曲同工之處。因此，首先將本文算法在自然圖像上進行驗證，來體現所提出的算法在主動輪廓模型圖像分割上的優勢，實驗數據集來自Describable Textures Dataset(DTD)數據集[16]和MSRA數據集[17]。然后，進一步將本文算法運用于選取的苗族服飾圖像上，驗證本文算法的分割性能以及對初始輪廓曲線的位置與形狀的穩定性。苗族服飾圖像數據集來源于北京服裝學院民族服飾博物館(http:∥www.biftmuseum.com/)，該博物館收藏有中國各民族的服裝、飾品、織物、蠟染、刺繡等一萬余件，還收藏有近千幅20世紀20～30年代拍攝的極為珍貴的彝族、藏族、羌族的民族生活服飾的圖片。在其中選取了關于貴州省苗族服飾的局部圖像(包括苗族蠟染、刺繡、混合與簡單圖像)。

實驗在MatlabR2016a編程環境下，以3.3 ghz的Intel(R)內核和8 gb的計算機內存，在PC機上運行。實驗中固定參數：偽水平集函數u(x)在內部和外部區域分別設置為0.7和0.3，模糊隸屬度的加權指數m=2。常規參數：局部加權系數w(x,y)被(2k+1)×(2k+1)窗口截斷，局部加權窗口k=1，迭代次數上限為30，時間步長Δt=0.02，最小正常數ε=1，長度項與正則項的加權參數μ=0.1和ν=0.8，圖像全局內外權重α1、α2與局部內外權重β1和β2需根據圖像進行調整。其他對比模型除特殊說明外，其余參數均參考原文設置。

3.1 比較算法與評價指標

由于本文是將主動輪廓模型探索性的運用于苗族服飾圖像的分割，因此將本文算法與基于區域的主動輪廓模型，如LBF模型[7]、LIF模型[8]、局部與全局擬合圖像(Local and global fitted image, LGFI)模型[18]和HLFRA模型[10]進行實驗驗證，并綜合量化評價指標與視覺效果對算法的性能進行對比分析和結果討論。

為了定量評價上述模型的分割效率和準確性，使用迭代過程中所需的分割時間、迭代次數、Dice相似性系數[19](Dice similarity coefficient, DSC)和敏感性系數(Sensitivity, SN)對分割結果進行定量評價[20]。其中迭代次數與分割時間的多少主要體現了算法的收斂程度，算法的收斂速度快，則相應的迭代次數與分割時間會得到很大程度的降低。相反，如果算法的收斂速度慢，則迭代次數與分割時間也會增加。DSC反映的是算法的分割結果與真值結果之間的相似度，SN反映的是正確檢測超聲區域像素點和標準區域像素點總和的比值。DSC與SN兩個評價指標的值都在0到1之間，值越大，表明檢測結果精度越高。分別定義為：

(25)

(26)

式中：∩是交集運算符，N(·)是封閉集的像素數，A是給定算法的分割結果，B為真值分割結果，TP和FN分別表示真陽性和假陰性。

3.2 自然圖像分割比較分析

為了體現本文算法的性能，將本文算法與基于區域的主動輪廓模型，即LBF模型、LIF模型、LGFI模型和HLFRA模型在自然圖像上進行對比實驗。圖1中圖像1至圖像6的實驗參數α1、α2、β1和β2分別設置如下：(1.0, 0.5, 1.0, 0.5)、(0.01, 0.01, 1.0, 1.0)、(1.0, 0.5, 1.0, 0.5)、(1.5, 2.5, 1.0, 2.5)、(1.5, 2.5, 1.5, 2.0)、(0.5, 3.0, 1.0, 3.0)。分割結果如圖1和表1所示，圖1中顯示了不同模型與本文算法對自然圖像的分割結果，第1列是具有初始輪廓曲線的原始圖像，第2列到第6列分別顯示的是LBF、LIF、LGFI、HLFRA模型與本文算法的最終演化結果。表1顯示的是不同模型在圖1中6幅圖像的迭代次數與分割時間。

圖1 不同模型對自然圖像的分割結果

由圖1與表1的分割結果可以看出，LBF模型相較于LIF模型來說分割結果相對較好，但是LBF模型所需的分割時間卻比LIF模型要高。LIF模型由于只運用了圖像的局部信息，在分割多目標圖像時容易導致邊界泄露，從而導致分割效果不佳，但是所需的分割時間較為可觀。LGFI模型的分割結果較差，由于LGFI模型運用了局部與全局圖像信息，所以其分割所需的時間最多。HLFRA模型能有效的對圖像進行分割，但是也存在一些不理想的地方被分割出來的情況。由于HLFRA模型是通過計算新舊能量函數的差值來更新偽水平集函數，所以只需要較少的迭代次數與分割時間。在本文算法中，結合了局部與全局模糊擬合圖像在Kullback-Leibler散度方面的圖像差異構造了模糊能量函數，同時在模糊局部與全局項之間考慮自適應權重。從而提高了本文算法對灰度均勻與不均勻圖像的分割精度與效率。此外，還在能量函數中添加了一項正則項與長度項來獲得光滑的輪廓曲線，平滑圖像邊緣。因此，本文算法相較于其他的模型來說，能夠很好的對圖像進行分割。并且只運用常用的標準梯度下降法最小化能量函數，就能獲得較少的分割時間與迭代次數。

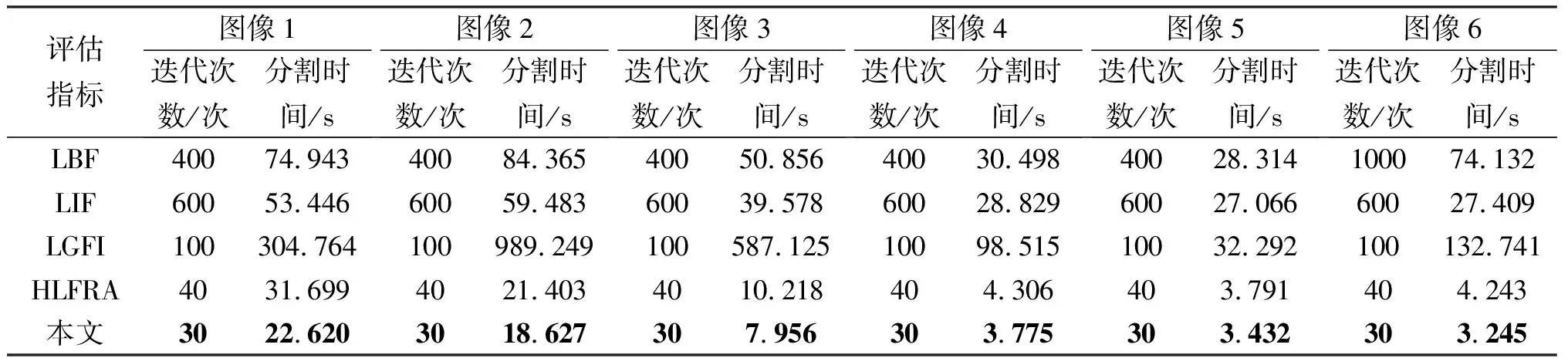
表1 不同模型在圖1中6幅圖像的分割時間與迭代次數

分割精度的DSC與SN系數如表2所示。從 表2 可以看出，本文算法相較于其他模型來說，具有較好的分割效果。對應圖像分割結果的相似性系數與敏感性系數分別能達到0.978與0.981以上，分割結果的平均值與LBF、LIF、LGFI和HLFRA模型相比分別提高了39.8%、67.2%、44.6%與5.8%。

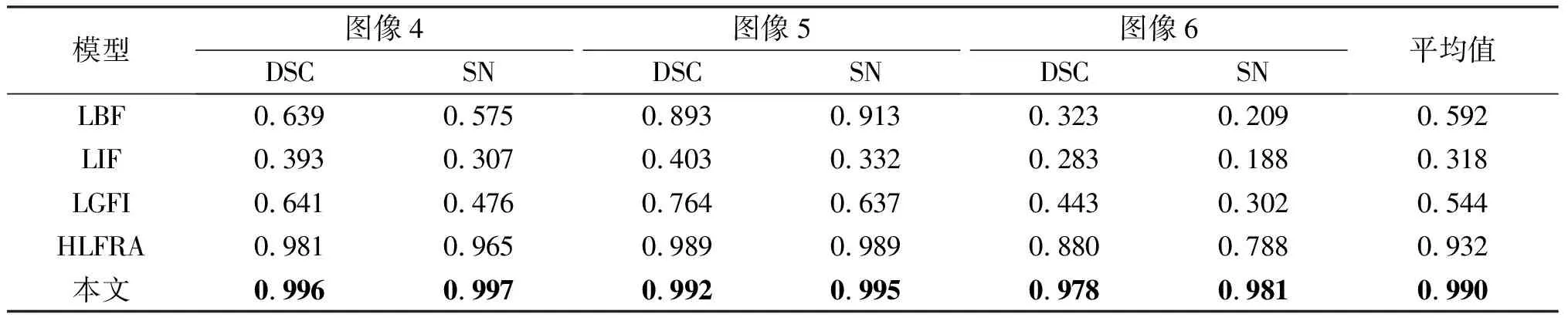
表2 不同模型在圖1中圖像4到圖像6的DSC與SN系數

3.3 苗族服飾圖像的分割

不同類型的苗族服飾圖像對分割結果也有一定的影響，如蠟染圖像中具有圖像破損、圖像不清晰、圖像形狀復雜等問題，刺繡圖像具有繡線紋理影響、圖像色彩差異較大等問題，以及混合與簡單圖像中不同類型圖像之間、圖案具有污點等問題的影響，這些問題都有可能導致得到的分割結果不理想。為了驗證本文算法對不同類型苗族服飾圖像的分割性能，將本文算法運用在不同類型的苗族服飾圖像上進行分割。如圖2所示，其中實驗參數α1、α2、β1和β2設置如下：除刺繡圖像中第一幅圖像與第二幅圖像以及混合與簡單圖像中第三幅圖像分別設置為(0.5, 2.5, 2.5, 2.5)、(1.5, 0.5, 1.5, 0.5)、(2.2, 2.0, 0.8, 0.7)，其他圖像的參數均設置為(0.01, 0.01, 1.0, 1.0)。

在圖2中，第1行、第3行與第5行分別顯示的是具有初始輪廓曲線的原始蠟染圖像、原始刺繡圖像與原始混合及簡單圖像，第2行、第4行與第6行分別顯示的是本文算法的分割結果。從分割結果看出，由于圖像不清晰、圖像破損、繡線紋理以及圖像色彩差異較大等問題的影響，導致部分分割結果不太理想，如蠟染圖像中第二幅圖像由于圖像的破損，導致一些不理想的區域被分割出來；刺繡圖像中第三幅圖像由于圖像的色彩差異較大，部分區域未能被提取出來等。但是，基于總體的分割結果而言，提出的算法在不同類型的苗族服飾圖像上具有較好的分割結果。

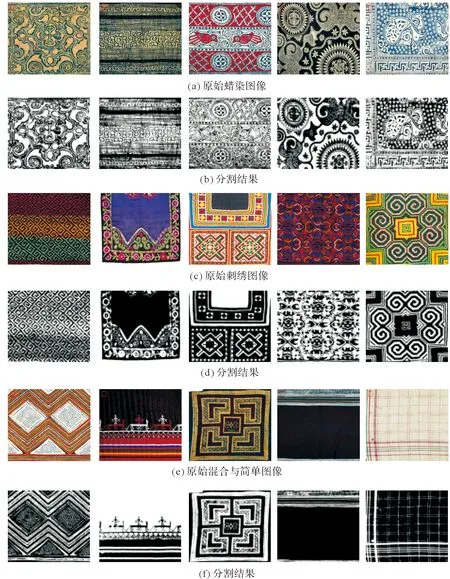
圖2 不同苗族服飾圖像的分割

3.4 苗族服飾圖像分割比較分析

為了驗證本文算法對不同類型苗族服飾圖像分割性能的差異性，將本文算法與基于區域的主動輪廓模型進行比較。圖3中圖像1到圖像9的實驗參數α1、α2、β1和β2設置如下：圖像1為(2.0, 2.2, 0.8, 0.7)、圖像2至圖像9設置為(0.01, 0.01, 1.0, 1.0)。圖3顯示的是不同模型在苗族服飾圖像上的分割結果。其中，圖像1到圖像3為蠟染圖像，圖像4到圖像7為刺繡圖像，圖像8到圖像9為簡單與混合圖像。第1列顯示的是具有初始輪廓曲線的原始圖像，第2列到第6列分別顯示的是LBF、LIF、LGFI、HLFRA模型與本文算法的最終演化結果。從分割的結果看出，提出的算法都能對這九幅圖像進行有效的分割。雖然一些特別細微地方的分割結果不是特別理想，但是相較于其他模型而言具有較好的分割效果。

進一步使用分割所需的時間與迭代次數定量評估了LBF、LIF、LGFI、HLFRA模型與本文算法對圖3中9幅圖像的分割性能。如表3所示，本文的方法對所測試圖像的分割時間都優于其他模型，只需要較少的迭代次數與分割時間就能對圖像進行分割。這是由于本文算法采用模糊局部與全局擬合圖像同原始圖像的差異構造了一個模糊能量函數，因此極大的降低了分割所需的時間。HLFRA模型從分割時間與迭代次數來看，具有較好的性能。LGFI模型相較于LBF模型與LIF模型來說迭代次數最少，但分割時間卻最多，因此LGFI模型在分割時間上不占優勢。LIF模型的迭代次數比LBF模型與LGFI模型多，但是所需的分割時間卻最少，所以LIF模型在分割時間上比LBF模型與LGFI模型好。

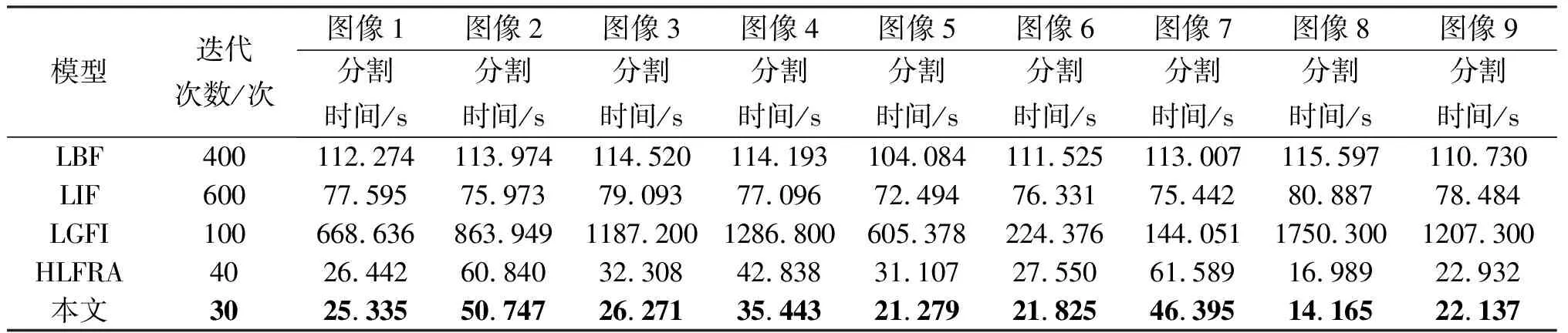
表3 不同模型在圖3中9幅圖像的迭代次數與分割時間

圖3 不同模型在苗族服飾圖像上的分割結果

3.5 初始化的魯棒性

初始曲線的形狀和位置對分割結果也有一定的影響。因此，在具有不同初始形狀和位置的苗族服飾圖像上，對初始曲線的形狀與位置的敏感性進行評估。實驗參數α1、α2、β1和β2設置為：(1.5, 0.1, 1.5, 0.5)。通過保持所有參數不變，對圖4中顯示的具有不同初始形狀和位置的服飾圖像進行測試。其中，第1行與第3行是具有不同初始形狀和位置的原始圖像，第2行和第4行是最終分割結果。結果顯示，對于不同初始形狀和位置的最終輪廓具有幾乎相同的分割結果，表明本文算法對初始輪廓的放置與形狀具有魯棒性。

圖4 不同初始形狀與位置的苗族服飾圖像

4 結 論

本文針對苗族服飾圖像的分割，提出了一種基于模糊擬合圖像驅動的苗族服飾圖像分割算法。在一定情況下起到發展苗族服飾的作用，這對苗族服飾圖案的保護、傳承和發展有重要的理論和實際意義。為了體現本文算法的有效性，首先，在自然圖像上與其他基于區域的主動輪廓模型進行實驗評估。結果表明，本文算法具有較好的分割性能。然后，將本文算法應用于苗族服飾圖像的分割。實驗結果表明，本文算法在苗族服飾圖像的分割中具有較好的分割結果，并且對水平集函數的初始化具有魯棒性。但是，本文提出的算法在分割苗族服飾圖像時同樣存在一些問題。作為探索性的研究，本文在以苗族服飾圖像為對象進行分割算法的研究時，僅僅考慮了簡單的苗族服飾圖像的形狀、紋理與色彩等圖像信息。對于圖案具有復雜度特別高、紋理非常突出、存在較嚴重的破損與色彩差異特別大等問題的苗族服飾圖像的分割結果中，存在少量漏分割與過分割的現象。這也將是今后的重點研究方向。