關于泡利矩陣的幾點討論

黃興奎

（荊楚理工學院 數理學院，湖北 荊門 448000）

0 引言

泡利矩陣是量子力學中的重要矩陣，目前所見文獻主要討論它的各種導出方法、在不同表象中的表示、解析量子力學中的典型計算問題等等。實際上，泡利矩陣是在討論電子自旋時引入的，不僅對于研究自旋問題、處理相對論性的狄拉克方程時非常方便，而且在量子信息、量子光學等新興學科中也有重要應用，可以從邏輯上實現量子非門X、量子位相門P（θ）、Hadamard門H，利用合適的脈沖就能從物理上實現上述量子門，從而為量子計算奠定必要的基礎。因此，討論泡利矩陣的性質，在量子力學理論中的基礎作用，以及在量子信息中的應用，有助于加深對于泡利矩陣的理解。

1 泡利矩陣的基本形式

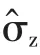
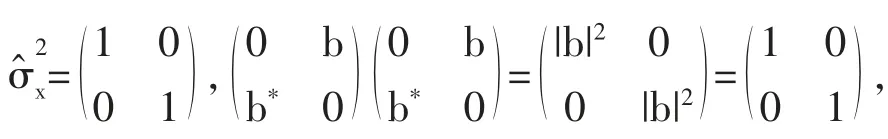
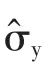
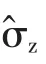
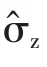
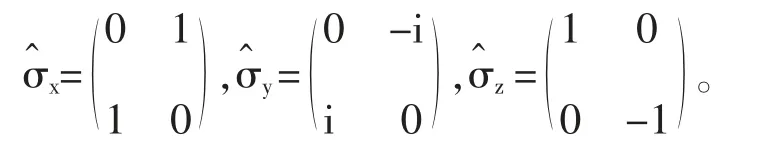
2 泡利矩陣的基本性質

為了后面討論問題的方便，簡單介紹一下泡利矩陣的基本性質。

（1）不對易性

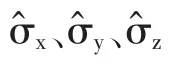
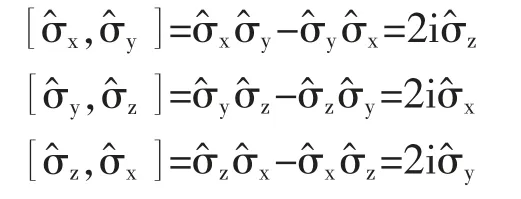
（2）反對易性

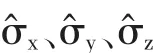
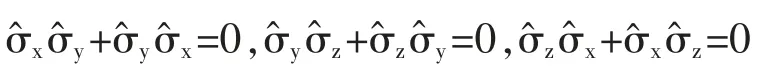
（3）自逆性

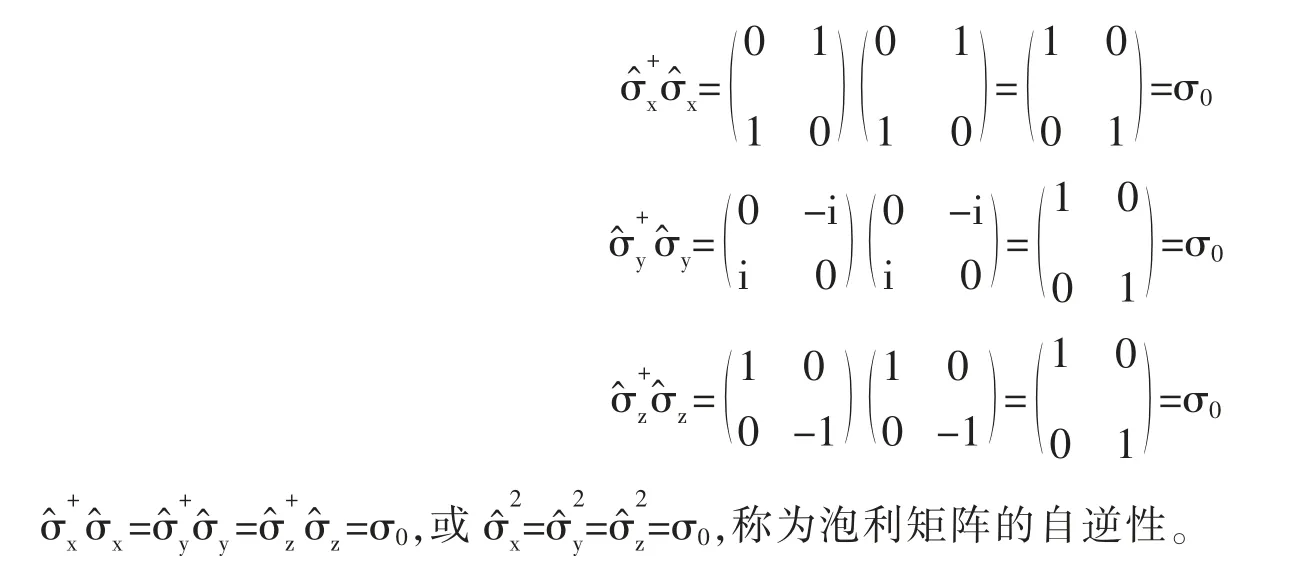
（4）零跡性

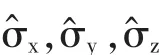
3 泡利矩陣在量子力學理論中的應用

3.1 展開任意厄米算符

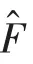
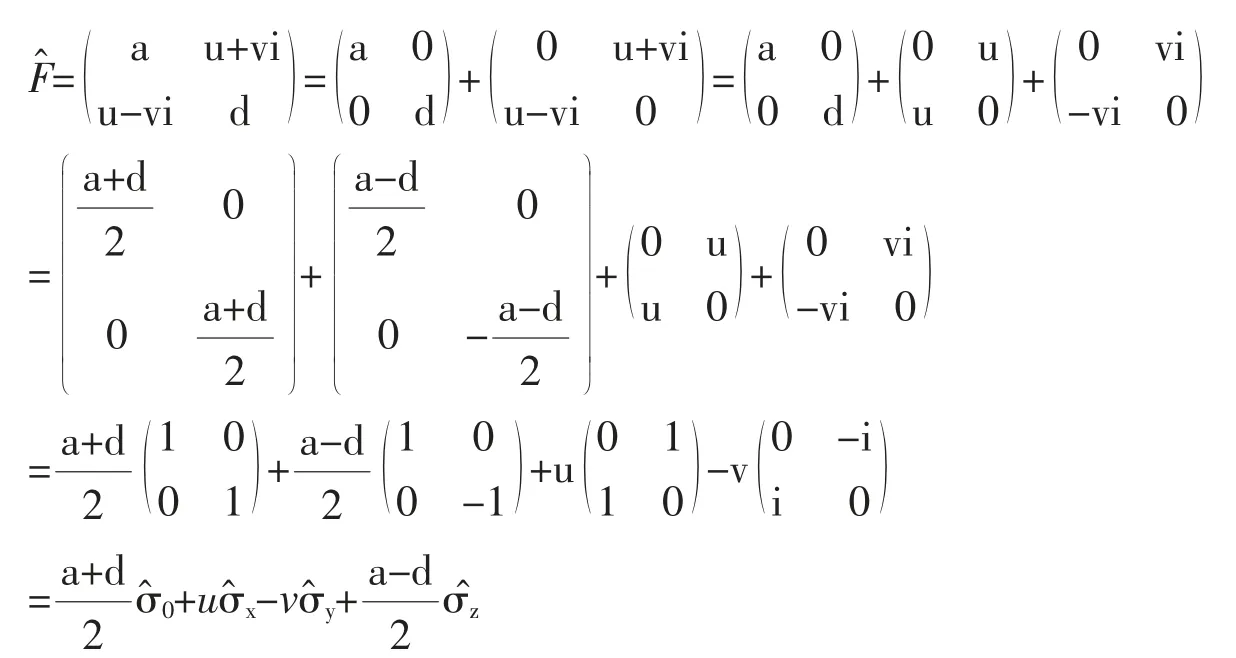
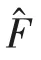
3.2 研究電子或其它粒子的自旋問題

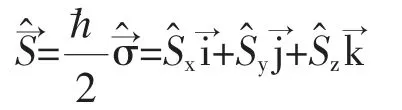
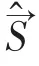
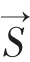
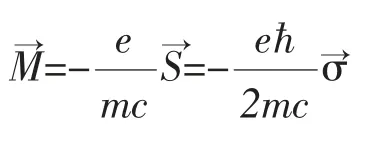
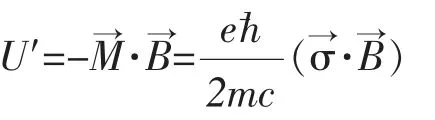
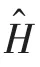
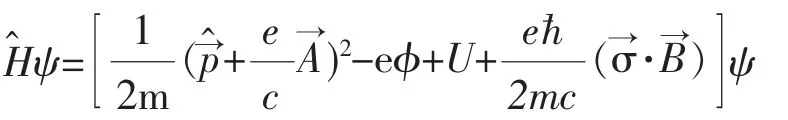
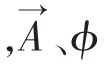
3.3 處理相對論性的狄拉克方程

薛定諤方程只適用于低能或非相對論的情況。研究高速運動的高能粒子，必須同時考慮狹義相對論和洛倫茲不變性。由于薛定諤方程對時間和空間的導數分別是一階和二階的，因此不是洛倫茲不變的。自旋是電子內稟的屬性，在非相對論情形下，泡利方程將自旋作為一種新的自由度添加到薛定諤方程上處理。在相對論情形下，狄拉克方程將自旋這個內稟自由度很自然地體現在該方程的旋量結構上，不僅如此，自旋與軌道耦合，自旋與自旋的耦合都可以包含在方程之中，而這一切，都離不開泡利算符的正確應用。

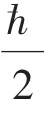
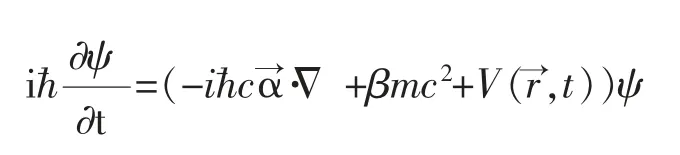
對定態問題，

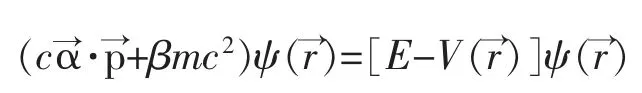
4 泡利矩陣在量子計算中的應用

量子邏輯門將輸入量子態變換成輸出量子態，單量子比特邏輯門是實現量子邏輯操作的基礎。常見的單量子比特門有量子非門X、量子位相門P（θ）、Hadamard門H。下面討論如何利用泡利矩陣實現這幾個門的邏輯功能，并簡單介紹其物理實現方法。

4.1 量子非門X

量子非門X的功能：將原子狀態由上能態|1〉變換成下能態|0〉或由下能態|0〉變換成上能態|1〉，即X|1〉=|0〉，X|0〉=|1〉，由于

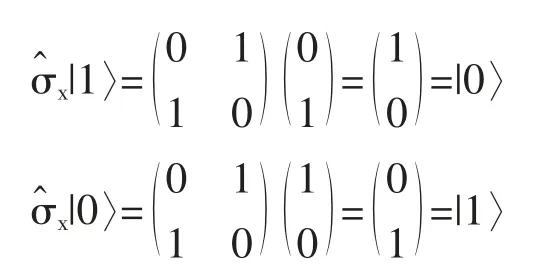
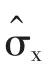
4.2 量子位相門P（θ）

量子位相門P（θ）的功能：P（θ）|0〉=|0〉，P（θ）|1〉=e|1〉。

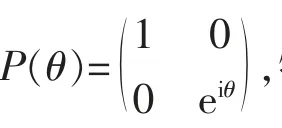
4.3 Hadamard門H

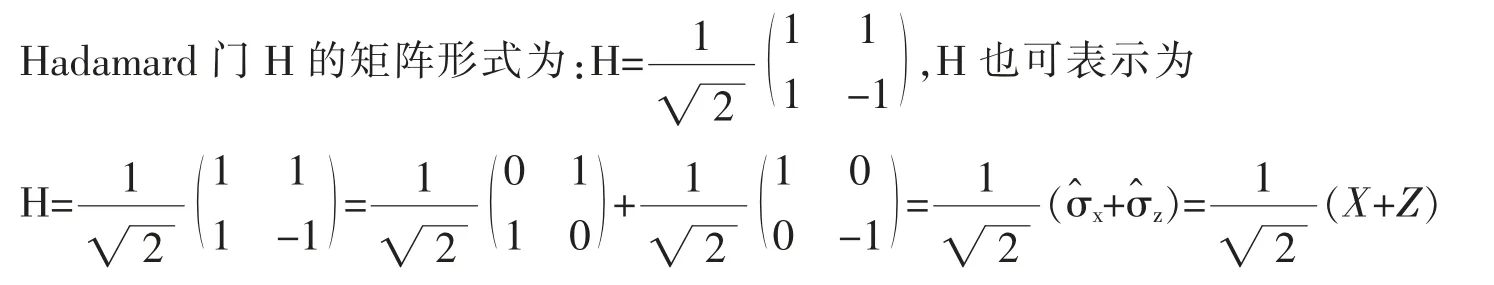
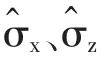
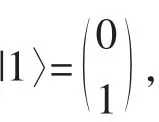
初始時處于上能態|ψ（0）〉=|1〉，則t時刻原子的量子態為：

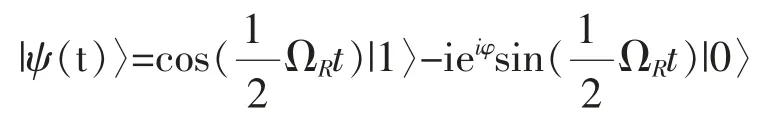
為討論方便取φ=0，則

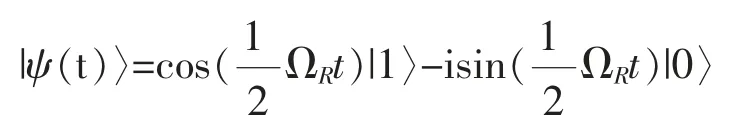
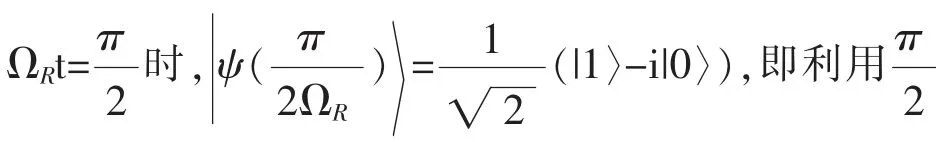
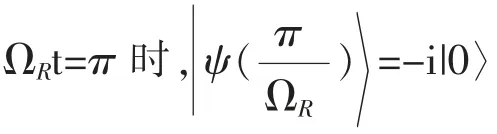
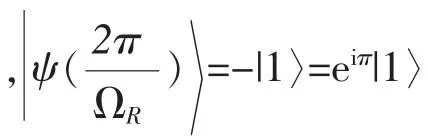
類似地，可以討論原子初始處于下能態|ψ（0）〉=|0〉的情況，這些結果在量子邏輯門的實現中均有重要的應用。

5 結論