傳聲器陣列聲壓級在線校準*

陳 勇 吳 鳴 楊 軍

(1 中國科學院大學 北京 100049)

(2 中國科學院聲學研究所噪聲與振動重點實驗室 北京 100190)

0 引言

近年來，戶外噪聲監測研究隨著環境噪聲污染的日趨嚴重而得到極大發展[1]。當在戶外環境中對某一目標噪聲源進行聲壓級測量時，為了有效抑制非目標聲源的干擾，胡文林等利用傳聲器陣列進行波束形成從而對目標信號進行增強[2-4]。常見的波束形成信號增強算法包括：延時求和波束形成法(Delay and sum beamformer,DSB)、自適應波束形成算法(包括最小方差無失真響應(Minimum variance distortionless response,MVDR)波束形成算法、線性約束最小方差(Linearly constrained minimum variance,LCMV)自適應波束形成器、廣義旁瓣相消器(Generalized sidelobe canceler,GSC))、多通道維納濾波器、后置濾波算法等。此外Wang等[5]提出一種基于最大期望值的迭代波束形成方法在一系列疊加的工業寬帶噪聲中有效監測出目標信號的功率值。為抑制戶外風噪對傳聲器監測的影響，Zhao等[6]利用便攜式剛性球形傳聲器陣列來減輕風噪聲，而保持目標低頻噪聲的聲壓級。另外在城市噪聲監測中，基于聚類的聲源分類算法[7-8]被使用以用于城市街區局域聲源監測。

微機電系統(Micro-electro-mechanical system,MEMS)傳聲器陣列由于體積小、價格低等優點，在進行聲源定位或者語聲增強中得到廣泛應用。當使用MEMS陣列進行波束形成時，隱含地假設陣列的每個通道都具有標準的頻響特性，但由于傳聲器、相關放大器和采樣組件的制造公差以及長期使用所帶來的老化問題，傳聲器通道之間存在較大幅值和相位誤差，導致MEMS傳聲器陣列并不能形成理想的波束形狀[9-11]，在進行噪聲測量時得不到準確的聲壓級值。因為器件老化是不斷緩慢進行的，在每次進行測量之前，均需要對傳聲器進行靈敏度校準。

對于需要長期在戶外工作的傳聲器陣列而言，在全消室中通過比對標準傳聲器與每個待校準傳聲器的頻域響應[12]，從而確定出真實的靈敏度的方法不僅費時費力而且不切實際。由于在進行戶外噪聲監測時，傳聲器陣列采集的信號是波束形成后的整體輸出，本文介紹了一種對傳聲器陣列整體進行在線聲壓級校準的方法。該方法基于一種計算量相對較小的到達時間差(Time difference of arrival,TDOA)聲源定位方法，利用環境干擾聲源的瞬態特性，在每個時頻點挑選出目標聲源的有效信號值，通過在線補償校準傳聲器與陣列輸出信號之間的目標聲源聲壓級差，從而校準傳聲器陣列測量的聲壓級。上述聲壓級校準實驗在全消環境中進行，通過比較不同條件下的聲壓級校準偏差的一致性，證明該校準方法具有較好的精確性和魯棒性，并且可推廣于任意一種陣型的傳聲器陣列測量裝置。

1 傳聲器陣列聲壓級在線校準方法

MEMS 傳聲器由于受工藝誤差和環境損耗等因素的影響，在頻域響應上產生失真，其靈敏度不斷退化。如圖1 所示，當傳聲器靈敏度發生退化后，波束形成的幅值響應會產生失真，從而使測量的噪聲聲壓級出現偏差。為了能夠實時校準傳聲器陣列，實驗中在陣列中心安裝了一個標準參考傳聲器，通過在線計算參考傳聲器與陣列間的聲壓級偏差，從而補償傳聲器陣列的誤差。當在多聲源干擾情況下，傳聲器陣列與參考傳聲器間的聲壓級差與無干擾時相同，則證明提出的戶外在線校準方法有效。

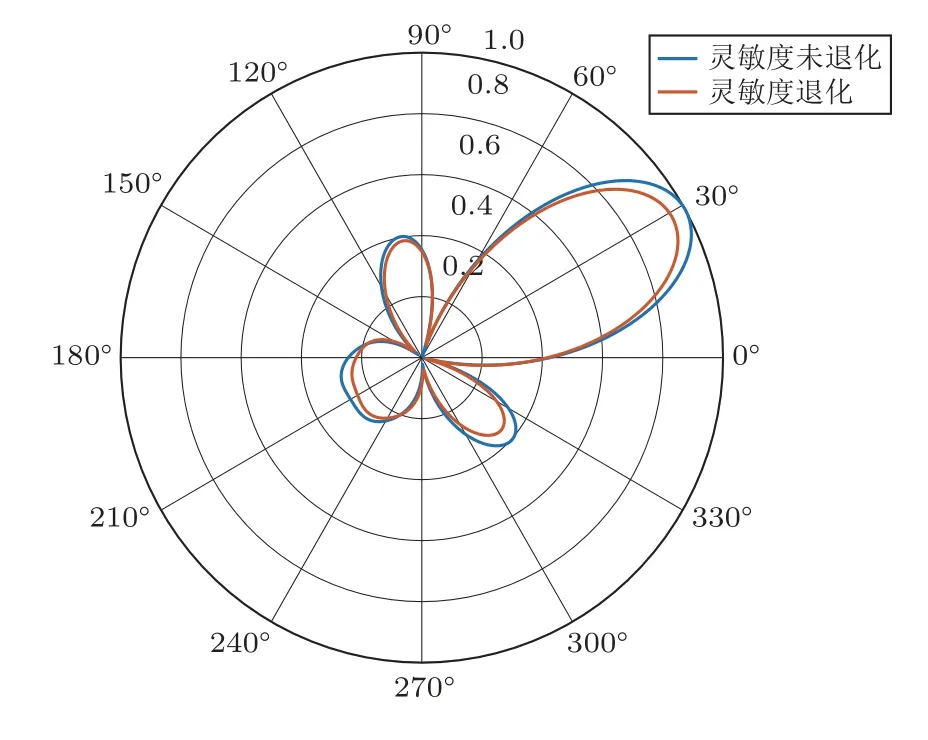
圖1 延遲求和波束形成仿真圖Fig.1 Delay and sum beamforming simulation

如圖2所示，聲壓級校準方法的主要步驟為：

圖2 聲壓級校準方法流程圖Fig.2 Sound pressure level calibration method process

(1)對采集信號進行短時傅里葉變換(Short time Fourier transform,STFT)，窗為海明窗。

(2)檢測每一幀信號是否來自于單聲源。

(3)對滿足單聲源條件的幀信號進行入射方向DOA估計。

(4)對目標方向單幀信號進行延遲求和波束形成(DSB)，并進行單頻點DOA 估計，剔除非目標方向干擾信號，將每一幀挑選出的時頻點信號累計在一個新的數組中，最后計算聲壓級。

(5)對參考傳聲器接收的數據，同樣進行單聲源和時頻點挑選，并累計起來，對最后累計起來的數值進行聲壓級計算。

(6)計算標準傳聲器與MEMS 傳聲器陣列之間的聲壓級測量值偏差。

1.1 單聲源檢測法

當傳聲器陣列在戶外進行噪聲測量時，接收到的信號往往受其他方向環境聲所干擾，因此需要判決每一幀信號是否來源于單一聲源。當傳聲器陣列記錄的信號只來源于一個聲源時，則傳聲器信號之間具有很強的相關性。所以為了檢測每一幀數據中是否主要由單一聲源信號組成，本文使用互相關方法來判決傳聲器對之間的比值是否接近于1[13]。

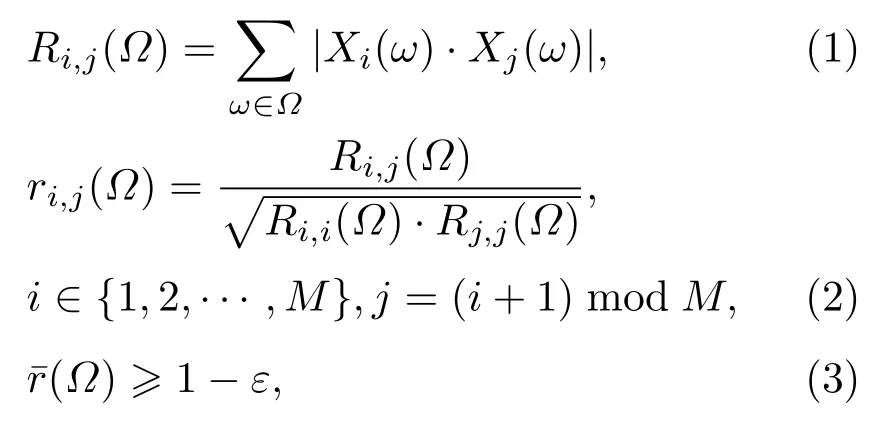
其中，Ω為角頻率點范圍，ε為一個較小的閾值，選擇為0.05。(Ω)為各對ri,j(Ω)的平均值。當前幀如果滿足公式(3)所示的條件時，則認為當前幀為單一聲源組成。然后對當前幀的聲源信號進行方向估計，當聲源方向為目標方向時，再進行接下來的計算。

1.2 TDOA估計方法

基于時延估計(TDOA)的聲源定位方法在線性陣列與環形陣列等多種陣型中得到大量展開[14]。由于環形陣列相對線性陣列具有分辨任意方向的能力且尺寸較小，在本文中使用一種利用均勻環陣的TDOA方法來估計聲源的入射方向。

圖3 顯示了一個均勻環陣分布著M個傳聲器，其中l是兩個相鄰傳聲器間的距離，r是環形傳聲器陣列的半徑，任意兩個相鄰傳聲器的夾角α為

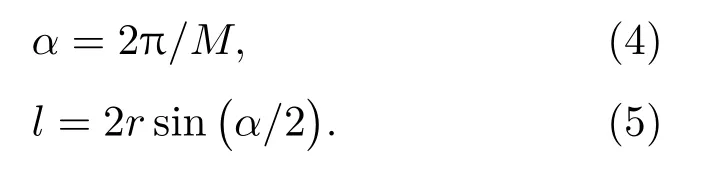
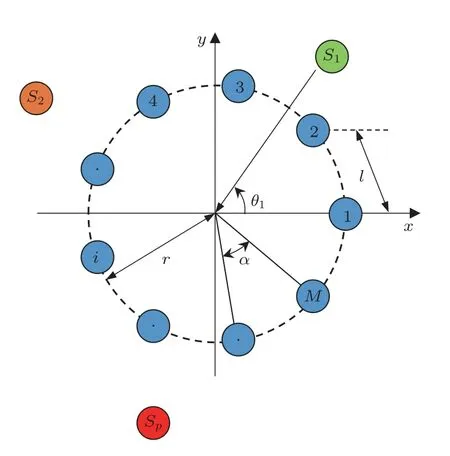
圖3 環形傳聲器陣列Fig.3 Circular microphone array

假設傳聲器陣列所處環境為二維平面自由場，任意傳聲器mi所接收的信號為

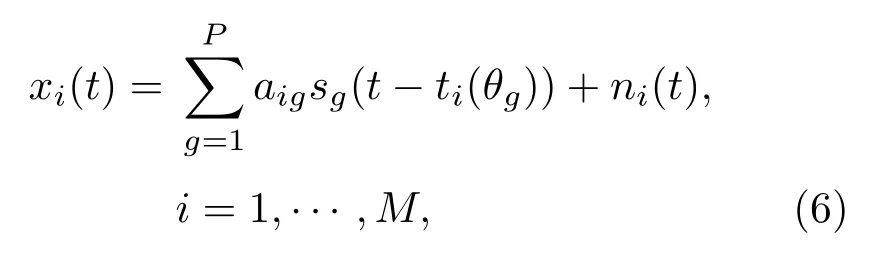
其中，aig是第i個傳聲器與第g個聲源間的傳播衰減因子，θg是第g個聲源的入射方向。假設在某一時間段內，僅有入射方向為θ的聲源s存在，則相鄰傳聲器對{i,i+1}接收到的信號之間的相對延遲如式(7)所示：

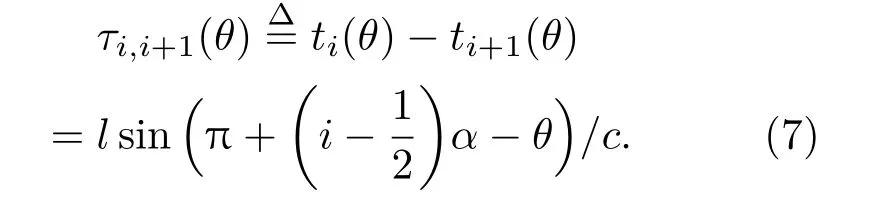
因此，第i個傳聲器接收的信號xi(t)可以由下列遞歸方程表示：

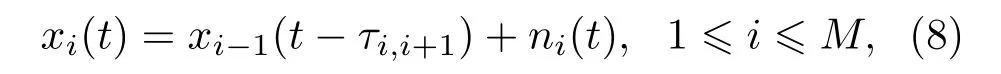
其中，ni(t)是傳聲器背景噪聲。假設Ri,i+1(ω)是信號xi(t)與xi+1(t)在頻域上的互相關函數，

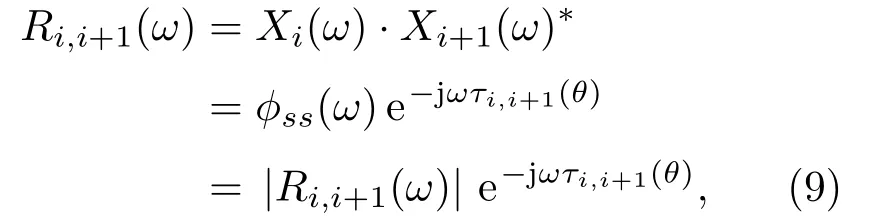
其中，Xi(ω)和Xi+1(ω)分別是xi(t)和xj(t)在頻域上的變換，ω為角頻率，φss(ω)是聲源s(t)的功率譜密度函數，則傳聲器對{i,i+1}之間的相位旋轉因子為

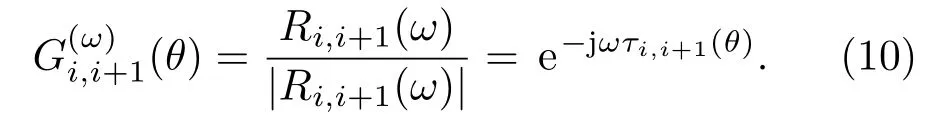
由于傳聲器對{mim1}接收到的信號之間的相對延遲τi→1(φ)為

φ為入射角自變量，則{i,1}之間的相位旋轉因子定義為

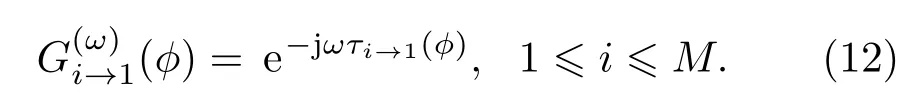
通過式(12)可以求出積分互譜：

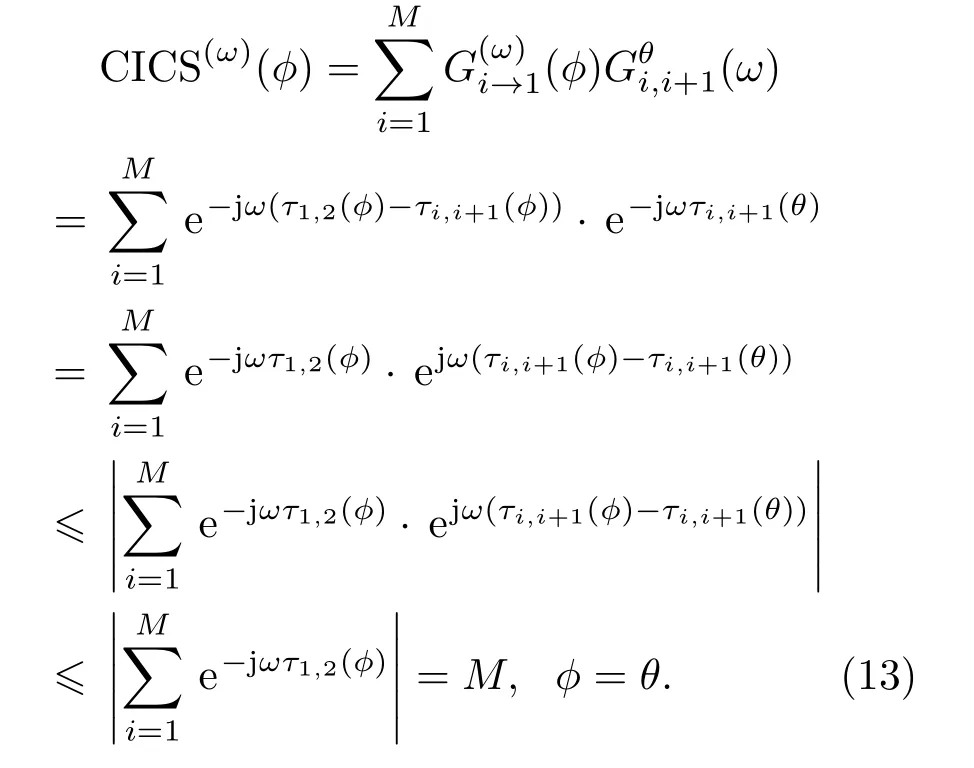
因此在判斷單一聲源的入射方向θ時，可以利用

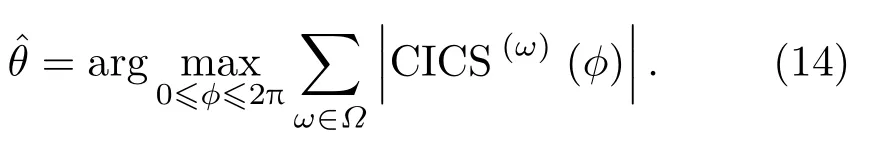
同理單頻點方向θ(ω)判決如下：

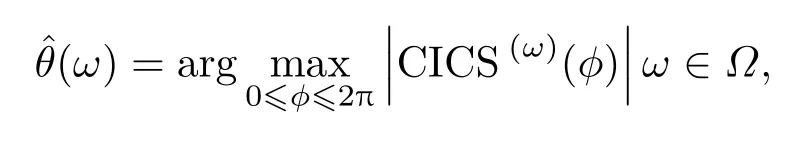
整個DOA判決過程如圖4所示。

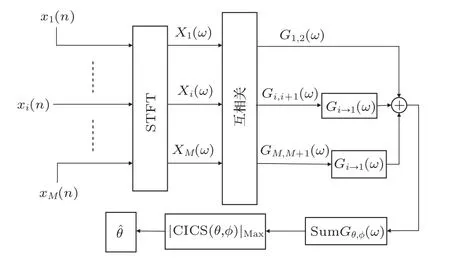
圖4 DOA 判決流程圖Fig.4 DOA decision process

1.3 聲壓級偏差計算

聲壓級偏差是指參考傳聲器測量聲壓級與傳聲器陣列測量聲壓級間的差值。當在干擾情況下計算的聲壓級偏差與無干擾情況下的聲壓級偏差相一致時，則證明本文提出的校準方法有效。時域上的聲壓級計算方法[15]如式(16)所示：

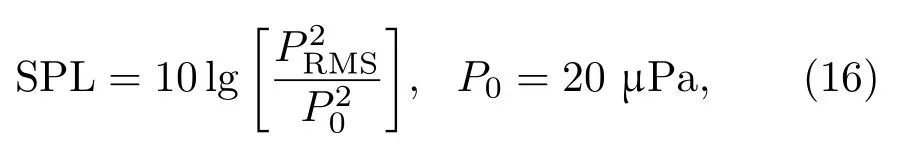
其中，代表平均功率值：

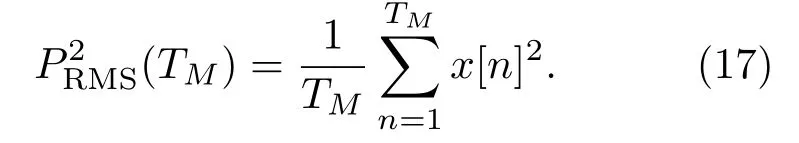
而根據式(18)的帕塞瓦爾定理，同樣可以在頻域上計算信號的聲壓級。

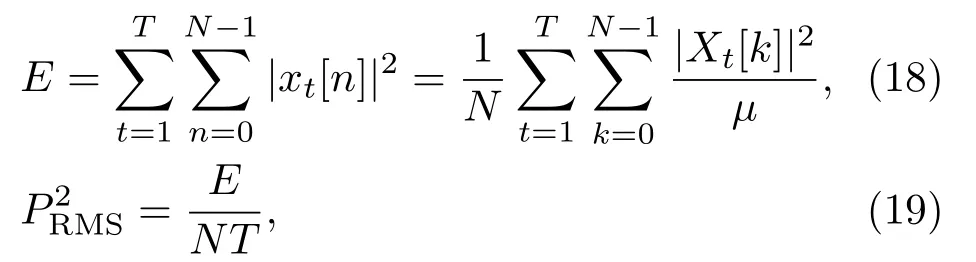
其中，N代表每一幀的長度，T代表總幀數，μ代表信號由于加窗時造成的能量損失系數。根據上述公式，對挑選出的頻點進行累計即可求出聲壓級，從而求出聲壓級校準偏差ΔSPL。

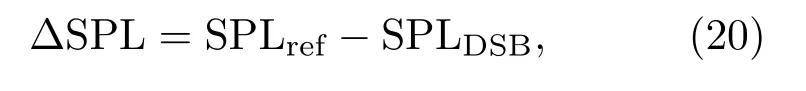
其中，SPLref表示參考傳聲器測量的聲壓級，SPLDSB表示陣列傳聲器進行延遲求和波束形成后測量的聲壓級。當校準偏差估算準確，則對傳聲器陣列信號補償偏差值即可校準測量的聲壓級。

2 目標聲源聲壓級校準實驗

2.1 相關參數及實驗平臺

考慮到戶外環境中有地面反射的影響，在半消實驗室中采集了實驗數據以驗證上述校準方法的準確性與有效性。實驗設備如圖5 所示，本實驗使用半徑為6 cm，具有9 個單元的均勻圓形陣列。根據空間奈奎斯特采樣定理，該陣列可有效分辨4000 Hz 以下的聲源信號位置。該陣列的傳聲器為MEMS 類型的SPH1642，標準傳聲器為BK-4189。聲源擺放距離傳聲器陣列4 m 遠處，高度與傳聲器陣列高度一致。目標聲源擺放在29°，干擾聲源擺放在100°和252°處，聲源同時發聲并通過BK公司的PULSE-3050 采集系統進行采集，系統的采樣率為48 kHz，采樣量化位數為16 bit，參考傳聲器的靈敏度為0.0498 V/Pa，陣列傳聲器的靈敏度未知，采用采集電壓信號來衡量其大小。對采集到的信號進行聲壓級校準處理，并驗證算法在不同噪聲干擾情況下的性能。

圖5 傳聲器陣列信號采集圖Fig.5 Microphone array signal recording

由于戶外監測的目標聲源通常是穩態聲源，而干擾聲源為非穩態的環境噪聲，干擾聲源通常具有短時間內平穩但長時間范圍內不穩定的特性。通過公式(2)計算出混合信號的互相關系數差值1-r(Ω)。圖6 為穩態流水聲與雞叫聲混合信號的互相關系數差值，當短幀信號僅包含單一聲源時，互相關系數差值為趨近于0 的穩定數值，如圖中紅線所示。當出現瞬態干擾信號時，互相關性系數差值相較于單一平穩信號會產生較大波動。因此為了能夠有效挑選出僅包含單一穩態聲源的單幀信號，要求干擾信號有大于單幀信號時間長度(40 ms)的暫停間隙。而常見的自然噪聲均滿足此條件。為此實驗中選取了符合條件的聲源類型作為測試對象，見表1。干擾噪聲為常見的動物鳴叫聲和周圍工廠的施工噪聲，這些噪聲源均具有聲音隨時間變化較大不會長期持續穩定存在的特點。

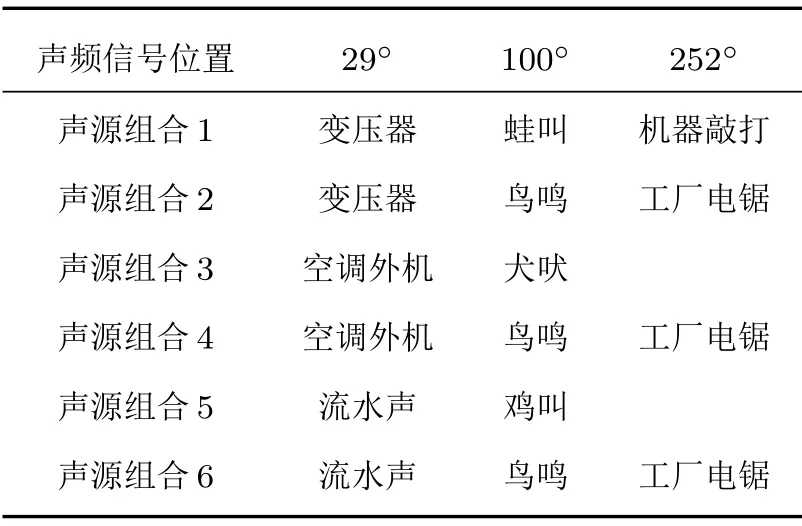
表1 采集聲源組合Table 1 Sound source combination

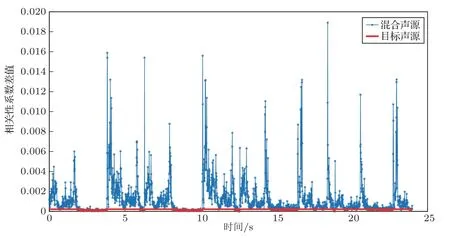
圖6 混合信號互相關系數時間分布圖Fig.6 Time distribution of mixed signal cross-correlation coefficient

2.2 實驗結果

如圖7 所示，噪聲源由目標方向的空調外機噪聲和干擾方向的鳥叫聲與工廠電鋸噪聲組成，由圖2 所示，先挑選出僅來源于目標方向聲源的單幀信號并進行波束形成，單幀信號長度為2048。由于挑選出的單幀信號在部分頻率點上仍有干擾聲源與目標聲源重疊的問題，需要在每一幀信號下挑選出純凈的頻率點信號。考慮到干擾聲源的稀疏性和時變性，在較長時間下可以在全頻率范圍內挑選出僅來源于目標方向的純凈信號。由于單頻點DOA估計算法準確率存在一定誤差[16]，所以選擇保留?θ(ω)∈29±5°的頻率點信號，對于挑選出的信號進行累計并計算出目標信號的聲壓級偏差[17]。

圖7 TDOA 法估計聲源位置Fig.7 Estimate the location of the sound source by TDOA

為了驗證實驗方案的有效性與精確性，首先計算了直接進行波束形成的聲壓級偏差，校準偏差取5次測量值的平均，實驗結果見表2。

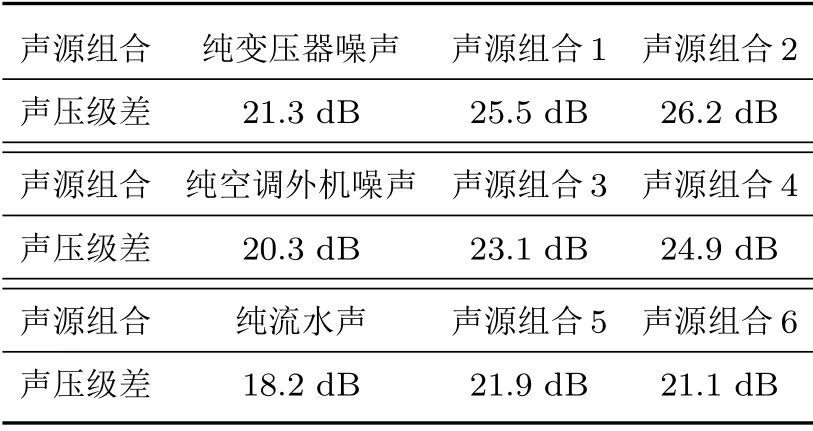
表2 無算法處理下的聲壓級估計偏差Table 2 SPL estimation deviation without algorithm processing

然后對混合噪聲進行頻點挑選處理，再計算聲壓級校準偏差，實驗結果見表3。

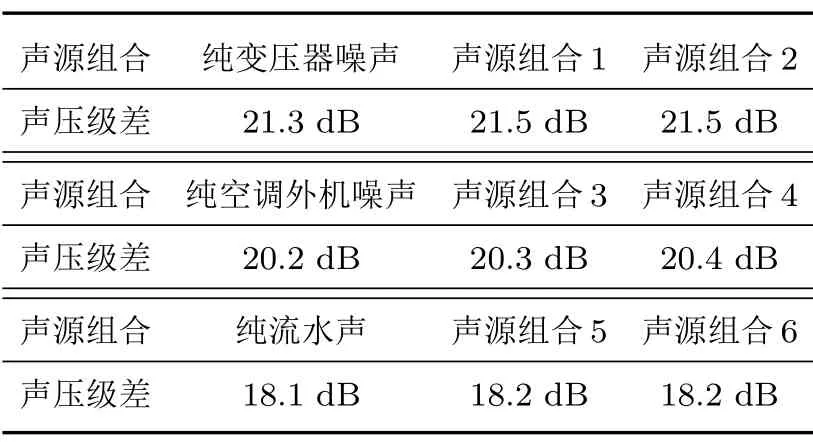
表3 算法處理后的聲壓級估計偏差Table 3 SPL estimation deviation without algorithm processing

從表2中可以看出，3種不同類型的目標聲源具有不一樣的聲壓級差值，這是由于陣列傳聲器在低頻范圍內的頻率響應衰減較大，當聲源頻率集中在低頻部分時，信號衰減較多，從而導致傳聲器陣列測量的聲壓級偏小。而參考傳聲器具有理想頻率響應，這使得具有不同帶寬分布的目標聲源之間具有不同的聲壓級差值。另外由于參考傳聲器接收的信號為各個方向的混合噪聲，而傳聲器陣列接收的信號是進行波束形成增強(DSB)后的目標噪聲，因為波束形成可以有效抑制非目標方向的噪聲信號，噪聲抑制量在4 dB 左右，從而使得聲壓級偏差與無干擾情況下的值相差較大。

而從表3 中可以看出，利用時頻點挑選法得到的聲壓級差和無干擾下得到的聲壓級差相近，且分布較為均勻一致，誤差在0.3 dB 之內。具體偏差分布如圖8 所示，由此可以證明介紹的算法準確性較好，將實時計算的聲壓級偏差補償給傳聲器陣列即可進行有效在線校準。由于使用的聲源都是戶外常見的自然聲，因此證明該方法可用于在戶外干擾情況下進行傳聲器陣列的在線校準。當使用其他結構的傳聲器陣列如三維球型陣列監測全空間范圍內的聲源時，只要陣元間距滿足奈奎斯特空間采樣定理時，修改陣型的幾何結構信息，該校準方法即可推廣于任意一種陣型的傳聲器陣列噪聲監測裝置。

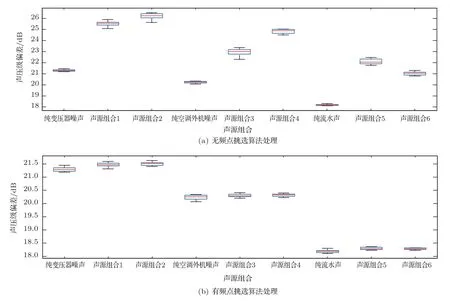
圖8 聲壓級估計偏差分布圖Fig.8 Distribution of SPL estimation deviation

由于本文提出的戶外傳聲器校準方法基于目標聲源定位和波束形成增強算法，目標聲應為遠場點聲源。當目標聲源為寬范圍聲源時，定位準確性性能下降，從而使校準聲壓級差值偏差較大。而當干擾噪聲為馬路噪聲等寬范圍聲源時，干擾聲源與目標聲源方向應相距較遠，聲源角度偏差10°以上，從而避免由于同方向干擾聲源的影響，降低校準性能。

3 結論

本文介紹了一種適合于在戶外進行目標噪聲監測時對MEMS 傳聲器陣列整體進行聲壓級在線校準的方法。該方法通過TDOA估計法對實時采集到的信號進行有效挑選，計算出標準傳聲器與陣列整體間的聲壓級偏差，通過補償該偏差從而達到對傳聲器陣列進行在線校準的目的。文中通過實驗對比了多種聲源干擾下與無干擾下的聲壓級校準偏差的一致性，偏差的誤差值保持在0.3 dB 之內，證明該方法具有較好的精確性和魯棒性。由于核心算法是利用TDOA估計法對時頻點進行挑選，所以只要修改陣列形狀的幾何信息，即可推廣于任意一種陣型的傳聲器陣列噪聲監測裝置。