軸向運動形狀記憶合金矩形薄板的主共振分析
李香港
(天津理工大學機械工程學院,天津 300384)
形狀記憶合金是一種智能材料,以其特有的形狀記憶效應和偽彈性[1],被廣泛用于機械、土木、醫療器械、航天等多領域,目前對于形狀記憶合金結構動力特性的研究已普遍展開。文獻[2]根據形狀記憶合金多項式函數本構關系,建立了形狀記憶合金梁橫向振動的非線性動力學方程,利用平衡態定性分析法分析討論了外載荷、溫度對系統動力穩定性的影響;文獻[3]引入范德波爾項,建立了形狀記憶合金遲滯非線性動力學模型,研究了隨機激勵下形狀記憶合金懸臂梁的分岔特性;文獻[4]研究了動態載荷下形狀記憶合金梁的響應特性;文獻[5]基于動力學奇異性理論,研究了形狀記憶合金層合梁的分岔現象,分析了激勵參數、形狀記憶合金層厚度等因素對系統減振效果的影響。本文針對軸向運動的形狀記憶合金矩形薄板進行分析,研究系統發生主共振時的穩態響應,分析薄板尺寸、外載荷、軸向運動速度等因素對系統穩態響應的影響。
1 軸向運動形狀記憶合金矩形薄板的動力學方程
1.1 形狀記憶合金多項式本構關系
根據文獻[6],將形狀記憶合金應力-應變關系表示為一個五次多項式,即:

式(1)中:a1、a2、a3為多項式系數;T為溫度;TM為馬氏體相變溫度。
馬氏體臨界溫度以下,馬氏體相穩定;奧氏體臨界溫度以上,奧氏體相穩定。應用多項式函數來表示形狀記憶合金本構關系更容易得到復雜系統的動力學方程。
1.2 軸向運動形狀記憶合金矩形薄板的動力學建模
假設形狀記憶合金矩形薄板長為a,寬為b,厚度為h,密度為ρ,阻尼系數為c,薄板在x軸方向的移動速度為v,如圖1所示。
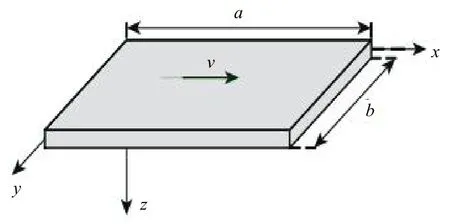
圖1 軸向運動形狀記憶合金矩形薄板示意圖
軸向運動矩形薄板的平衡方程為:

由式(1)可知,對于薄板,非線性應力-應變關系可表示為:


式(3)中:μ為泊松比;εx、εy、γxy為應變分量。
設u0、v0為薄板中面沿x、y軸的位移,可得:

薄板的幾何方程為:

厚度為h的矩形板的內力矩表達式為:
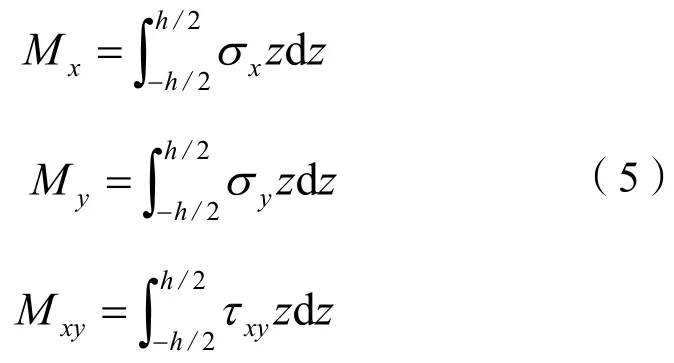
將式(4)代入式(3)中,可得非線性應力-應變表達式,再將3個表達式代入式(5),對Z坐標沿厚度h的方向進行積分,最后將結果代入式(2)中得軸向運動形狀記憶合金薄板的振動方程,為:

式(6)中:


2 系統受迫振動分析
2.1 四邊簡支邊界下薄板的振動微分方程
假設強迫激勵P=fcos(ω0t),考慮四邊簡支薄板的邊界條件,取位移模式如下:

通過伽遼金法將振動方程及位移模式離散化,可得振動微分方程:

式(7)中:

2.2 多尺度法求解
應用多尺度法進行求解,引入小參數ε,微分方程表示為如下形式:
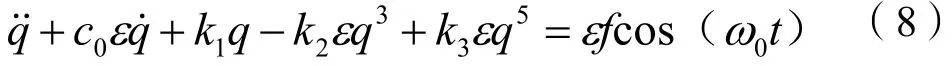
矩形薄板的橫向位移展開式:

將式(9)代入(8)中,并忽略ε的高階項,得:

方程的通解為:

將通解(11)代入式(10)中,并消除久期項,可得:

將A表示為極坐標形式:

式(13)中:a為幅值;θ為相角。

將式(14)(15)代入式(13)中,分離實部和虛部,并引入新的變量γ=σT1-θ,對于系統的穩態運動情況,令˙=γ˙=0a,得到a和γ的常值解。
可以得到薄板系統的幅頻響應方程:

式(16)中:a為共振幅值;σ為頻率。
3 數值算例與結果分析
對于形狀記憶合金薄板,給定參數如下:c=0.2,a1=523 MPa,a2=1.868×107MPa,a3=2.186×109MPa,TM=287 K,μ=0.3,ρ=2.89×103kg/m3,h=0.05 m。用四階龍格庫塔法對多尺度法計算結果進行驗證后的主共振幅頻曲線圖如圖2所示。取參數a=0.5 m,b=0.5 m,v=1 m/s,P=5 kN。圖2 中,星號為數值計算結果,由圖2 可以看出,仿真結果與多尺度法所求的解吻合較好。

圖2 主共振幅頻曲線圖
3 種不同尺寸下軸向運動形狀記憶合金矩形薄板的響應曲線如圖3所示,由圖3 可見,薄板尺寸大小對系統主共振幅頻響應曲線的幅度有重要的影響,小尺寸薄板響應曲線的幅度要遠小于大尺寸薄板響應曲線的幅度。也就是說,當薄板尺寸減小時,響應幅值會出現不同程度的減小。所以,在實際應用中,可通過減小尺寸來降低薄板主共振振動幅度。

圖3 薄板尺寸對幅頻響應的影響
不同軸向運動速度下形狀記憶合金薄板系統的響應曲線如圖4所示。隨著軸向運動速度的增大,曲線沿頻率方向發生明顯的平移,但幅值未發生明顯變化。這表明,軸向運動速度的變化會對共振頻率產生一定的影響,但并沒有使響應曲線發生定性變化。

圖4 軸向運動速度對幅頻響應的影響
不同外載荷下軸向運動形狀記憶合金薄板系統的響應曲線如圖5所示。由圖5 可見,隨著外載荷增大,響應曲線沿頻率方向發生平移。與軸向運動速度相似,外載荷變化只影響共振頻率,未對響應曲線產生定性影響。

圖5 外載荷對幅頻響應的影響
4 結論
本文研究了軸向運動形狀記憶合金矩形薄板在外載荷作用下的主共振問題,推導了矩形薄板的振動微分方程。并通過多尺度法求得薄板系統的幅頻響應方程。對系統的主共振問題進行數值分析,結果顯示:薄板尺寸增加,振動幅值增大;軸向運動速度與外載荷只影響共振頻率,軸向運動速度增大,共振頻率增大;外載荷增大,共振頻率減小。

