球體斜碰撞下包裝材料能量傳遞及轉換的試驗研究

王慶朋，李威，王恒，王振鋒，李德峰，徐廣印

球體斜碰撞下包裝材料能量傳遞及轉換的試驗研究

王慶朋1,2，李威1，王恒1，王振鋒1,2，李德峰1，徐廣印1,2

（1.河南農業大學 機電工程學院，鄭州 450002；2.農產品冷鏈物流信息與裝備技術河南省工程實驗室，鄭州 450002）

針對在球體斜碰撞過程中，包裝材料界面能量變化及其量化表征的問題，基于碰撞接觸面的幾何特征，提出外加能量吸收率、傳遞率和轉換率的計算模型。首先，分析球體斜碰撞接觸面的幾何特征，利用基圓和滑移面面積建立能量吸收率、傳遞率，以及不同方向能量比率的數學表達式。然后，通過搭建球體自由跌落斜碰撞測試平臺，分析沖擊角、襯墊厚度、跌落高度、球體直徑和材料密度對能量參量的影響。通過碰撞接觸面積計算能量吸收率和轉換率，遵循了能量守恒定律，具有可行性；能量吸收率在75%以上，并隨著跌落高度、球體直徑和密度增加而變大，而沖擊角對能量吸收率的影響較小；法向能量比率隨著沖擊角增加、球體直徑減小而下降，切向能量比率與此相反，跌落高度和密度對能量比率無明顯影響；在給定工況下，襯墊的最佳吸能厚度為4 mm。文中的分析有助于包裝材料碰撞界面處能量變化以及接觸特性的研究。

包裝材料；斜碰撞；接觸面積；能量吸收；傳遞與轉換

為了避免產品在流通過程中因受到振動和沖擊等外加載荷作用而產生破損，合理的緩沖包裝是必不可少的，這對整個系統的動態響應、接觸表面摩擦和磨損等都有著重要影響[1-3]。

目前，針對碰撞界面問題已經有很多研究，主要研究方法有連續碰撞力和沖量動量等。在連續碰撞力方法中，經典的完全彈性接觸模型不考慮能量消耗，是該類分析的基礎[4]。在實際碰撞過程中，接觸材料并不是完全彈性變形，而存在黏彈性、塑性等，耗散了一定能量。為了分析接觸過程中能量變化，常將卸載視為彈性過程，加載和卸載曲線所圍面積即為能量耗散[5-6]。球體接觸狀態從完全彈性變形發展為彈性–塑性→彈性–混合彈塑性–塑性→彈性–混合彈塑性→混合彈塑性，已有文獻主要分析了沖擊角、材料硬度和硬化指數等對能量耗散的影響[5-6]。上述研究方法的不足之處是不能較好地表達界面應力分布和變化過程，因此，數值方法在該研究領域得到廣泛的應用。Messaadi等[7]利用有限元方法對球體在與重力方向呈30°、45°和60°夾角下進行斜碰撞分析，隨著角度增加，球體接觸時間減少，而接觸面積和接觸壓力變大，等效剪切應力在夾角為45°時達到最大值，相應的磨損體積較大。Nishida等[8]對鋁合金球體進行了超高速斜碰撞分析，當沖擊角較小時，碰撞界面近似為圓形；而當沖擊角大于40°時，則為類橢圓。類似地，Stropek等[3]、謝若澤等[9]和Key等[10]對梨、合金鋼和復合材料等碰撞過程中能量耗散、損傷特性等進行分析。

基于動量沖量方法，主要考慮碰撞前后運動狀態變化，應用比較廣泛的模型有Walton、Maw和Stronge等。在碰撞界面不僅存在回彈作用，還存在黏著、滑動和滾動等[2,11-13]，運動狀態的變化由法向回彈系數和摩擦因數等表達，而黏著的程度由表面能等表達，進而分析系統的能量變化規律。Doménech-carbó等[2,13]采用獨立摩擦回彈的建模方法，假定球體材料回彈和摩擦獨立存在，能夠同時考慮界面特征參量的變化。韓維等[14]基于瞬態摩擦和切向恢復系數，采用步進沖量方法求解斜碰撞問題。在試驗方面，Dong等[15]通過鋼球自由跌落斜碰撞前后運動狀態，分析在不同沖擊角下回彈系數和回彈角等變化，當沖擊角大于20°時，界面狀態從黏著發展為滑動。類似地，Cross等[16]、馮斌等[17]和Ireland等[18]對鋼球、馬鈴薯和橡膠球等碰撞過程中回彈系數和能量耗散等進行了測試分析。

目前，關于球體與包裝材料在外加載荷作用下的碰撞問題，研究者往往重視碰撞前后運動狀態變化，而忽視界面處能量吸收、傳遞和轉換過程；再者，斜碰撞界面存在滑移狀態，Dong等指出[15]，如何量化表征界面參量變化還存在問題。鑒于此，基于球體斜碰撞接觸面的幾何特征，提出外加能量在界面處的吸收率、傳遞率，以及不同方向上能量比率的數學表達式，通過搭建球體自由跌落碰撞測試平臺，分析沖擊角、襯墊厚度、跌落高度、球體直徑和密度對能量參量的影響，為碰撞過程中包裝材料界面能量變化和接觸特性分析提供基礎。

兩組治療有效率比較，實踐組采取復方丹參滴丸與曲美他嗪聯合應用治療，實踐組治療有效率明顯高于對照組，兩組對比，差異有統計學意義（P＜0.05）。見表1。

1 球體斜碰撞界面能量變化分析與表征

1.1 碰撞界面能量變化分析

具有一定能量的球體以沖擊角與平板發生斜碰撞，如圖1a所示，在接觸界面處，一部分能量在法向轉換為材料應變能，另一部分則在切向轉換為應變能和摩擦耗能。當材料發生黏性、塑性變形和內部微觀結構變化時，消耗相應的能量，在形式上表現為00（n、t分別為法向和切向回彈系數，為摩擦因數）。在已有文獻中，更多的是通過回彈系數分析法向、切向的能量耗散，該類方法不足之處：這些參數僅代表某一方向某種狀態的變化，不具有關聯性，并且不能充分說明能量耗散的作用機制；不能有效地表達界面處能量的影響范圍以及材料損傷程度。針對這些不足，有必要改進表征方法。受到外加載荷作用的球體在碰撞界面表現為接觸面積，根據經典的完全彈性接觸理論[5-6]，如果僅存在法向載荷，則接觸面為規則圓形；如果界面存在滑移，則為類橢圓[7-8]，如圖1b所示。碰撞界面處接觸面積能夠直接體現能量傳遞和轉換關系，這有利于在更小尺度方向上分析碰撞體（如球體、包裝材料等）力學性能參量的變化規律。

1.2 碰撞界面能量變化表征

為了分析球體斜碰撞過程中包裝材料界面處能量吸收、傳遞和轉換關系，通過接觸面積進行表征計算。由于法向壓縮和切向滑移，接觸面形狀既不是規則圓形，也不是橢圓，而是這兩者的結合。實際接觸面包括基圓和滑移面2部分，如圖1b所示，基圓與2倍的滑移面面積之和為橢圓面積。通過采用分層材料的測試方案，即含有和去掉包裝材料的2種形式，分別獲得頂層和底層碰撞界面接觸信息，進而計算相應的能量參量。在包裝材料的頂層和底層界面處基圓面積分別為：

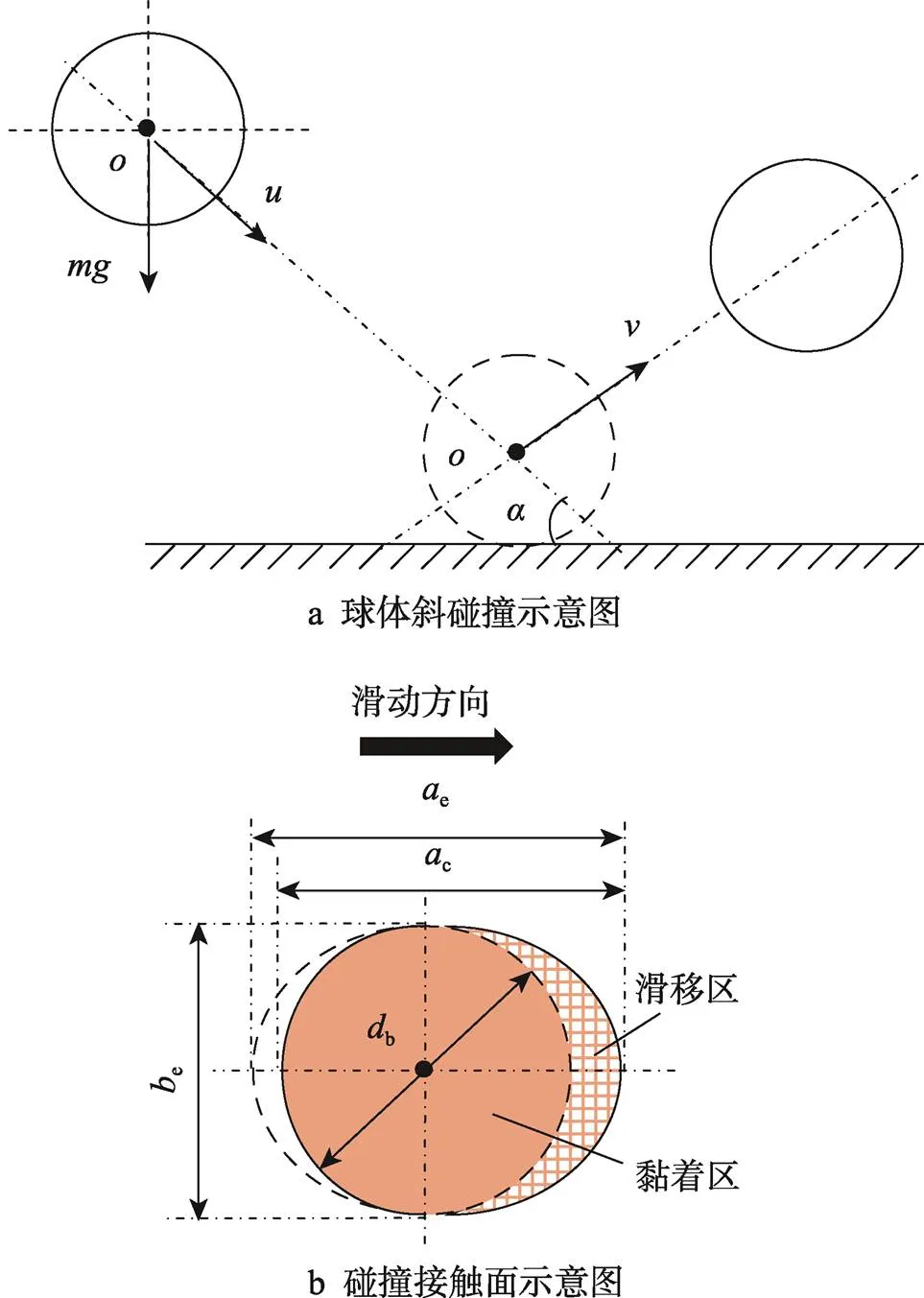
圖1 球體斜碰撞及其界面特征

式中：b_u、b_d分別為頂層和底層接觸面基圓直徑。

球體在斜碰撞界面處產生一定滑移，相應的虛擬橢圓面積為：

翻漿冒泥病害治理的工程設計、預算與施工，要求提供比較準確的翻漿冒泥病害范圍的數據，尤其是翻漿冒泥病害底界里程和深度的數據。翻漿冒泥病害區域的描述如圖1所示。

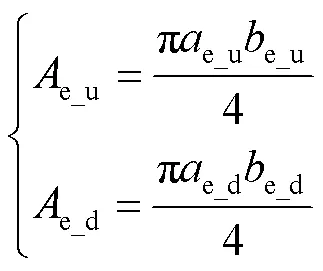
式中：e_u、e_u和e_d、e_d分別為頂層和底層接觸面對應橢圓的長軸和短軸尺寸。

滑移面積為橢圓與基圓面積之差的一半，即：

在自行設計的測試平臺進行球體自由跌落斜碰撞，如圖2所示，利用軸承、支撐塊和懸置細線調節平板的傾斜角度以及球體的跌落高度，分別通過鋼尺（得力工具有限公司，型號DL8100，精度為1 mm）和角度儀（韋度電子有限公司，測量范圍0°～90°，精度為0.02°）進行測量。通過可調電壓直流電源（Wanptek，型號KPS605DF，0～60 V，0～5 A）供電，電路中設置開關控制電磁吸鐵（伊萊克電氣有限公司，型號ELE–P25/20，DC24 V-8 kg），當開關斷開，電磁吸鐵磁力消失，球體自由跌落，與鋼板發生碰撞。在鋼板上鋪設一張打印紙（210 mm× 150 mm×0.096 mm），并且在其上邊覆蓋一張薄型復寫紙（127 mm×90 mm×0.028 mm），通過千分尺（韋度電子有限公司，0～25 mm，精度為0.001 mm）測量接觸面長軸c和短軸c，存在c=b/2+e/2和c=b=e，利用式（1）、（2）和（4）分別計算得到基圓、橢圓和接觸面面積，進而獲得能量吸收率和轉換率。

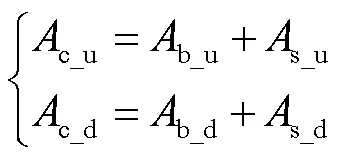
根據式（4）可得傳遞到底層的能量比率為：

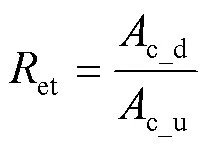
為了分析球體斜碰撞過程中包裝材料（如瓦楞紙板、珍珠棉板、泡沫網袋、氣泡膜和橡膠襯墊等）界面處能量參量的變化規律，將直徑為30 mm的鋼球從高度400 mm處自由跌落到傾斜30°的鋼板上，獲得不同材料對應的接觸形狀，見表1。從測試結果來看，由于這些材料內部結構不連續、不一致，如瓦楞的頂端和空隙部分、珍珠棉板的大變形、網袋的連接部位、氣泡的破裂等，將導致接觸形狀及其邊緣不規則，從而使測量結果存在很大的不確定性。相比之下，橡膠襯墊能夠獲得較規則的接觸形狀。

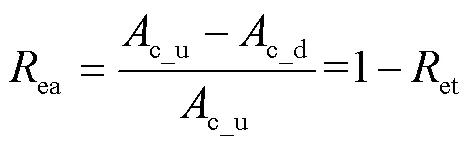
頂層材料吸收能量后，法向和切向的轉換率分別為：

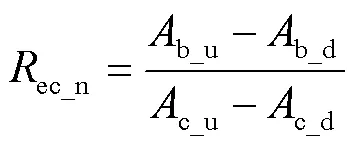
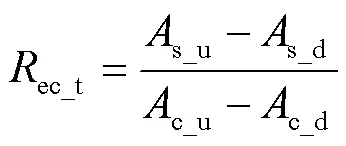
將式（7）和式（8）求和得：

將式（4）帶入式（9）可得：

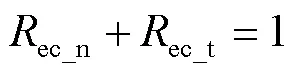
從式（6）和式（10）可以看出，當頂層材料吸收外加能量后，一部分轉換為法向壓縮和切向運動，另一部分則傳遞到基底材料，該過程遵循能量守恒定律。

為了分析球體斜碰撞界面能量轉換問題，利用接觸面積計算外加能量的吸收率和法向、切向上的轉換率，通過不同碰撞工況研究能量參量的變化規律。

2 界面能量變化測試方法和試驗平臺

森林資源作為自然賦予人類重要的資源、作為我國重要的資源之一，是人們賴以生存的天然氧吧，不但能夠調節環境氣候，而且還蘊含著重要的經濟價值，與人們的生產生活密切相關。近些年來，由于人們不合理的開發森林資源、濫砍濫伐現象較為嚴重，在一定程度上加劇了森林資源的短缺局勢，降低了森林的環保功能。基于此情況下，相關部門要加強對森林資源的培育與管護，合理的開發利用森林資源，堅持走可持續發展的戰略，守候著人們的天然氧吧。

南川地處重慶南部，轄3個街道、31個鄉鎮，面積2 602平方公里，人口66.1萬人，其中農業人口55.4萬人。2011年出欄生豬 61.73萬頭，禽兔 502萬只，肉牛 2.88萬頭，肉羊 2.72萬只，中蜂6.22萬群。近年來，南川區畜牧獸醫部門強化“免疫、檢疫、監測、監管”綜合管理措施，確保了無重大動物疫病發生、無肉食品安全事故發生，保障了以生豬為支柱，以南川雞、金佛山中華蜜蜂、涪陵水牛為特色的南川畜牧產業持續快速發展。南川區連續多年被上級評為獸醫工作先進單位，許多創新的管理模式，一直處于全市乃至全國同行業領先水平，并多次代表重慶市接受了農業部領導工作調研和檢查。

Gray clustering evaluation of university engineering survey laboratory safety management based on COWA

2.1 球體斜碰撞測試方法

球體碰撞測試方法主要有自由跌落和鐘擺試驗等，由于球體碰撞后存在回彈運動，為了減小外界因素的影響，文中采用球體自由跌落的方法。將球體懸置于一定高度，常采用手動操作、氣動吸盤和電磁吸鐵等控制球體釋放。手動操作很容易導致球體發生旋轉，帶來人為誤差；氣動吸盤需要專門的氣源和氣路，較為復雜；電磁吸鐵具有操作簡單、響應速度快等優點，并且測試結果的一致性較好，因此，文中采用直流電磁吸鐵進行控制。

關于界面處接觸面積的獲取方法，目前，主要通過薄膜壓力傳感器或者材料損傷壓痕獲得。薄膜傳感器很大程度上會改變碰撞接觸狀態，不適合界面問題的研究；直接測量材料壓痕的前提是界面能夠產生損傷，而多數斜碰撞不會產生明顯壓痕或損傷。文中采用在碰撞界面放置一張薄型復寫紙的簡單方法，既能減少對碰撞材料的影響，又可以獲得明顯的壓痕。

11月22日，京東物流配送機器人智能配送站啟用儀式在湖南長沙舉行。隨著載有用戶包裹的配送機器人編隊依次發出，全球首個由機器人完成配送任務的智能配送站正式投入使用。首個京東配送機器人智能配送站位于長沙市科技新城，占地面積600平方米，設有自動化分揀區、配送機器人停靠區、充電區、裝載區等多個區域，可同時容納20臺配送機器人。當包裹從物流倉儲中心運輸至配送站后，站內裝載人員按照地址將包裹裝入配送機器人，再由機器人配送至消費者手中。從配送能力來看，配送站最高設置每天2000個包裹的配送量，能夠為周邊5公里居民提供物流配送服務。截至目前，京東配送機器人已在全國20余個城市實現落地。

較多的本地流動攤販選擇在游客量較多時在固定的擺攤點做生意而且一般平時生意收入并不太可觀，一些店商家在旅客高峰期生意會有所好轉，另一些靠近該小鎮的學校依靠學生為長期客源生意情況平時才不至于虧損。

2.2 試驗測試平臺

球體碰撞界面處接觸面積為：

圖2 球體斜碰撞試驗測試裝置

3 結果與分析

其余能量則被頂層材料吸收，即：

表1 球體與包裝材料斜碰撞接觸形狀

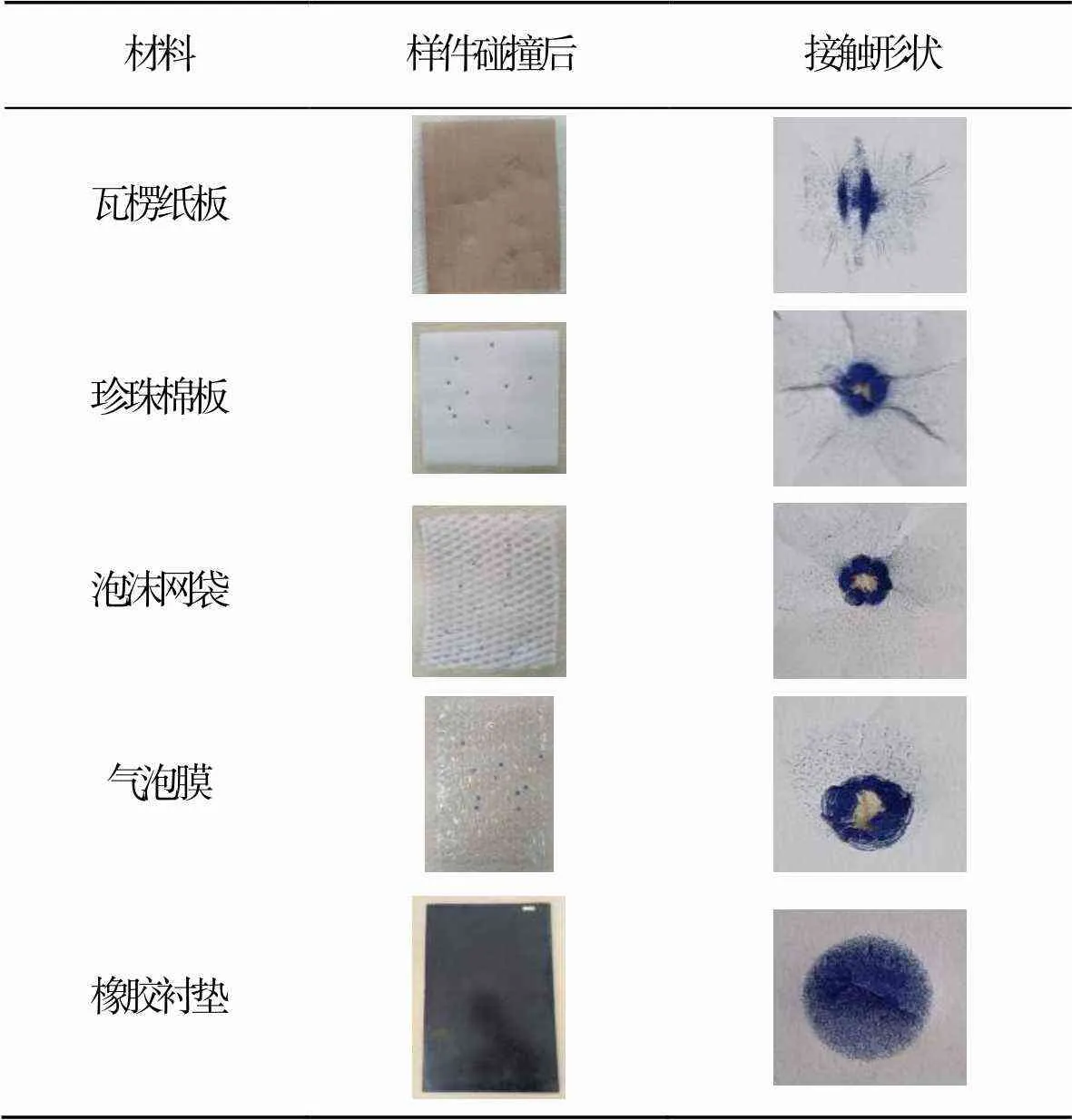
Tab.1 Contact surface of oblique impact between sphere and packing materials

利用Thornton等[12]提出球體法向碰撞彈性和塑性接觸模型，如式（11）所示，分析接觸力與接觸面積的變化關系。

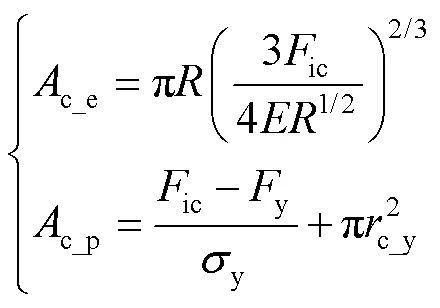
式中：ic為實測接觸力；為有效彈性模量；y、c_y和y分別為屈服狀態下對應的接觸力、接觸半徑和接觸應力。

IEET工程教育認證不設置任何量化的指標[7-8]，主要以學生畢業生具備專業核心能力，并評估畢業后3-5年的專業知識及技能、實務執行與領導統御之基本能力、從事研究之基本能力、培養服務社會之能力。進而進行專業調制和改進，達成具有自己的特色教育目標。其目的讓參與認證的專業依照各個專業的定位、行業標準、特色、學生背景及相關環境做出自己專業的學生應該具備的核心能力。并考核學生之學習成果，評量學系、研究所學程是否達到其自設的教育目標[9]，及其畢業生是否擁有進入職場應具備之基礎專業核心能力。其主要目的是為促進其建立并落實持續改善機制，不斷提高工程教育質量。

為了研究球體斜碰撞過程中能量參量的變化規律，以橡膠襯墊為研究對象（500 mm×250 mm，襯墊厚度用表示），使用邵氏硬度計（韋度電子有限公司，型號LXD–A，范圍為0～100HA，精度為0.5HA）測量橡膠襯墊的硬度為70HA。對沖擊角、襯墊厚度、跌落高度、球體直徑及其材料密度等因素進行測試，每種工況重復進行10次，取其平均值進行計算分析。

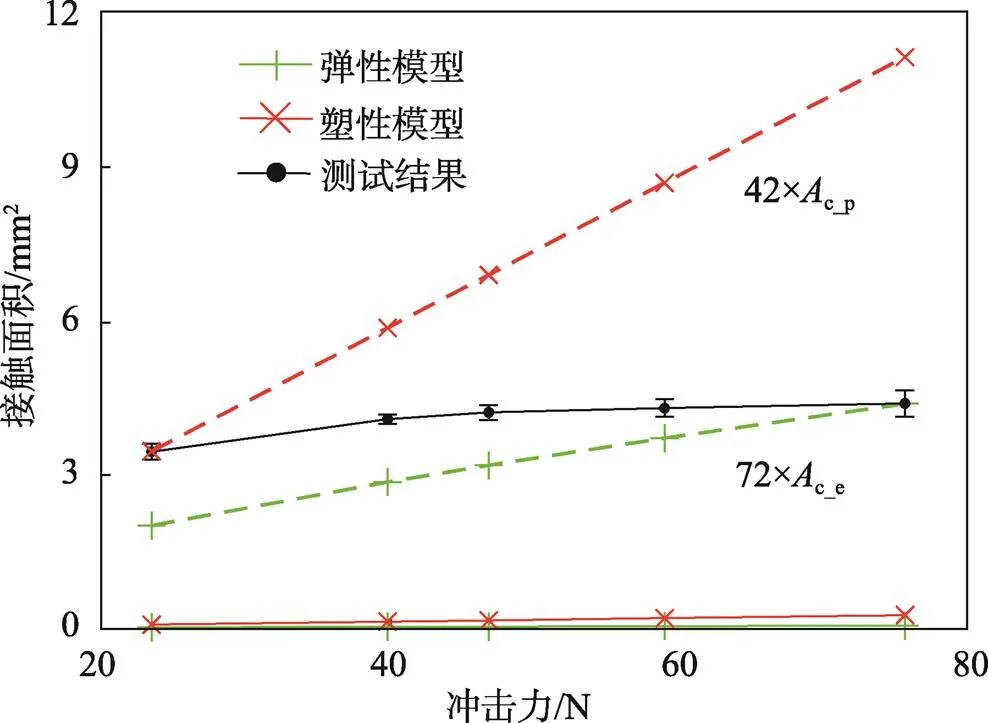
圖3 球體法向碰撞接觸模型與測試結果對比

3.1 沖擊角的影響

將直徑為30 mm的鋼球從高度400 mm處自由跌落到不同傾斜角的鋼板上，并且在上邊分別鋪設不同厚度（1、2、3、4、5 mm）的橡膠襯墊，其中，厚度為4 mm襯墊上不同沖擊角碰撞產生的接觸面及其尺寸見表2。鋼球與鋼板斜碰撞接觸面積、能量吸收率，以及能量比率與沖擊角間的變化曲線見圖4。

利用加速度傳感器（上海澄科，型號CT1002L，最大量程為250）和測試系統（NI，型號USB–6002 DAQ）進行測量，采用直徑為20 mm鋼球與鋼板法向碰撞，其他條件與前文的一致，計算過程中，=210 GPa，y=285 MPa。彈性和塑性模型的計算結果以及測試結果見圖3。由于打印紙和復寫紙的影響，實測面積比計算結果要大，將彈性、塑性模型的結果分別乘以72和42，實際的碰撞應該是混合彈塑性狀態，從測試后鋼板上留下的凹痕也可得到這樣的結論。因為采用的是同樣的基準，所以實際的混合彈塑性狀態并不影響能量參量的計算。

圖4a為球體斜碰撞接觸面基圓、滑移面面積與沖擊角間的變化曲線。當沖擊角較小時，沖擊力的法向分量大于切向分量，滑移面面積遠小于基圓面積，滑移特征表現得不明顯，文獻[2,13,15,16]將該狀態定義為黏著。從文中測試結果來看，將該狀態定義為黏著并不嚴謹，滑移面存在，只不過是面積較小而已。隨著沖擊角增加，沖擊力的法向分量逐漸變小，基圓面積減小；而切向分量增加，球體更容易運動，使得滑移面積增加。

圖4b為球體碰撞能量吸收率的變化曲線。若鋼球與鋼板直接碰撞，則界面處的材料將外加能量全部吸收；若在鋼板上鋪設橡膠襯墊，外加能量一部分被襯墊吸收，另一部分被傳遞到基底，這與式（6）是一致的，該過程符合能量守恒定律。沖擊角對能量吸收率的影響很小，能量吸收率基本恒定。厚度為1 mm的襯墊吸收約78%的能量，吸收率隨著厚度增加而變大，4 mm襯墊的吸收率達到最大值，約為88%。襯墊厚度從2 mm增加到4 mm，對應能量吸收的增加率分別為8.29%、2.63%和1.73%，隨后出現下降。可見，襯墊厚度存在一個最佳值。

（3）幣齡累積。幣齡累積是針對初期PoS共識機制的常見攻擊方式，不存在于PoW。因為持幣時間越長，獲得記賬權的概率越大。在攻擊者擁有足夠代幣之后，可以通過累積時間來達到控制網絡新生成塊的目的。在代幣足夠的情況下，攻擊者甚至可以將自身代幣分散于多個節點，這一攻擊方式可以幫助攻擊者多次生成有利塊，比如回滾以進行雙花攻擊。占有代幣1%的攻擊者可以通過2個月不進行交易來進行攻擊。基于同樣的理由，PoS可能出現冷啟動的問題。

廬山西海的旅游景點眾多但是開發較少，許多景點設置重復性高，布局也不太合理。許多旅游景點主要以觀光為主，養生旅游開發得較少，許多景區的代表性、感染力、參與度等都比較差。還處于低層次的發展階段，這樣就對廬山西海的旅游資源造成極大浪費。

在碰撞界面處，材料吸收外加能量后，法向和切向方向上能量比率的變化曲線見圖4c。當沖擊角較小時，能量比率變化很小，主要表現為材料的應變能；隨著沖擊角增加，法向能量比率下降，而切向的增加，從式（9）可看出，兩者之和為碰撞總能量，呈現為此消彼長的關系。對于不同厚度襯墊的法向能量比率，曲線存在一個急劇下降點，襯墊厚度越大，轉折點對應的沖擊角越小，襯墊厚度為1 mm時，對應的沖擊角為60°；襯墊厚度為2 mm和3 mm時，對應的沖擊角為50°；襯墊厚度為4 mm和5 mm時，對應的沖擊角為40°。換言之，材料越軟，界面處出現滑移對應的沖擊角越小，這主要是由于較軟材料吸收能量是有限的，當碰撞材料法向出現能量飽和時，則轉向切向方向發展。

表2 不同沖擊角下球體碰撞接觸面

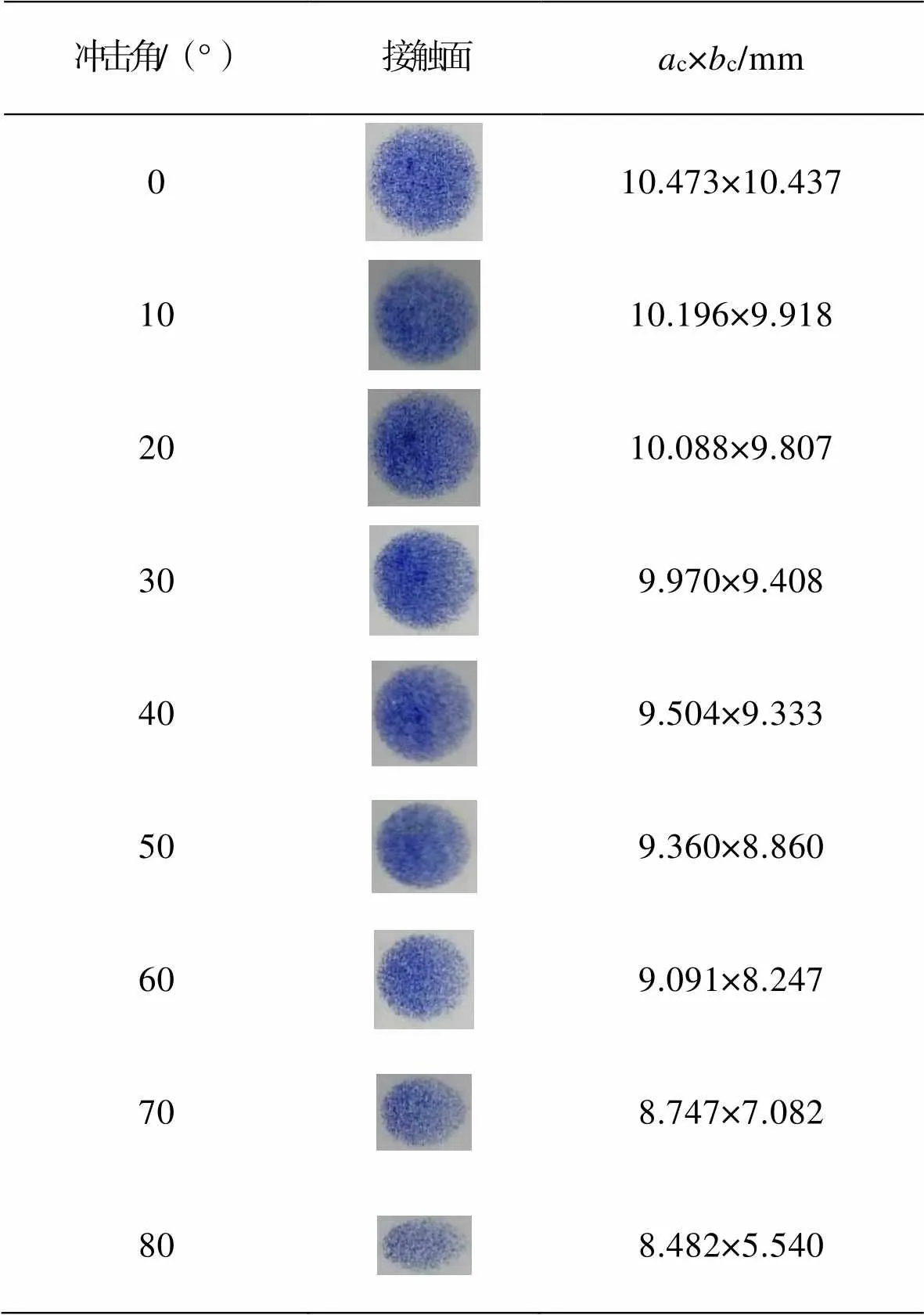
Tab.2 Contact surface of sphere at different impact angles

3.2 跌落高度的影響

將直徑30 mm鋼球從不同高度自由跌落到傾斜角30°的鋼板上，為了更清楚地表達界面面積的變化，僅描述無襯墊和襯墊厚度為2、4 mm的結果。由于法向和切向的總能量守恒，所以僅描述切向方向能量比率的變化，見圖5。

圖5a為碰撞界面基圓和滑移面面積的變化曲線，跌落高度從100 mm升至600 mm，面積基本為線性增加，這與彈性、塑性接觸理論是吻合的，無襯墊的基圓面積從6.00 mm2增至9.30 mm2，增加率為55.00%；襯墊厚度為2和4 mm的基圓面積分別增加77.81%和99.14%。雖然滑移面積也增加，但是變化特征沒有基圓的明顯，并且曲線存在一些波動。

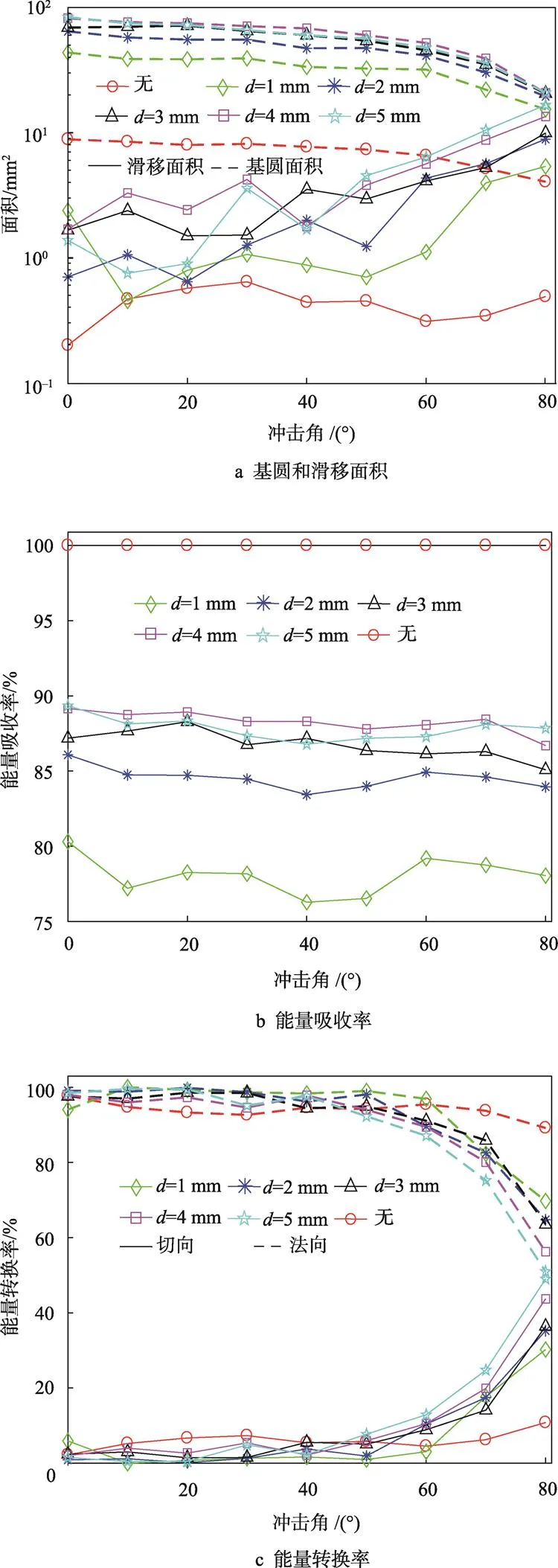
圖4 不同沖擊角下斜碰撞接觸面積和能量參量

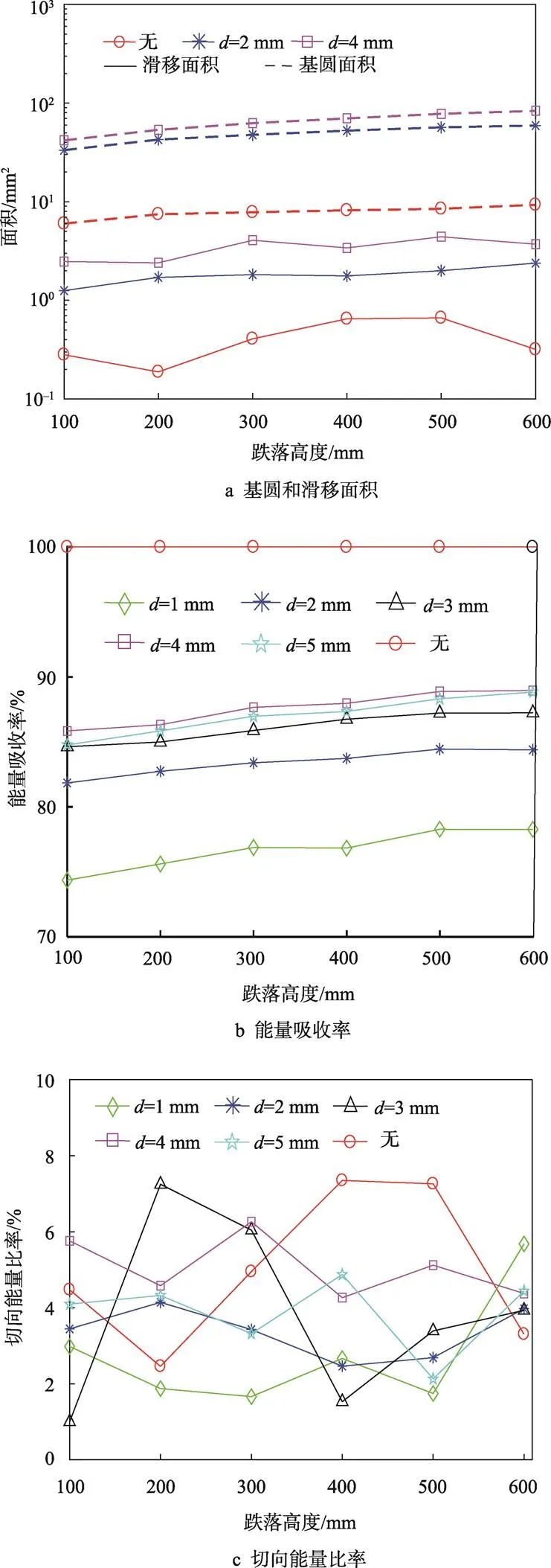
圖5 不同跌落高度下斜碰撞接觸面積和能量參量

圖5b為界面處能量吸收率的變化曲線，可以看出，能量吸收率隨著跌落高度的增加而略微變大。襯墊厚度為1 mm的吸收率從74.36%增至78.27%；襯墊厚度為4 mm的吸收率從85.85%增至88.96%，存在最大的吸收率。可見，跌落高度對界面能量吸收率的影響并不明顯。圖5c為切向能量比率的變化曲線，與3.1節的結果相比，跌落高度對切向能量比率影響較小。不同襯墊厚度的能量比率的計算結果基本在1%～8%變化，除了無襯墊和襯墊厚度為3 mm的結果存在較大波動，其他工況的結果隨著高度的增加變化均很小。無襯墊和不同襯墊厚度切向能量比率的均值分別為4.97%、2.77%、3.36%、3.86%、5.06%和3.86%，這主要是由于球體碰撞接觸面的基圓和滑移面面積是同步變化的。

3.3 球體直徑的影響

將不同直徑的鋼球從高度400 mm處自由跌落到傾斜角為30°的鋼板上，接觸面積、能量參量的表達方式與3.2節的類似，結果見圖6。

圖6a為不同直徑球體斜碰撞界面處基圓和滑移面面積的變化曲線，其變化規律與跌落高度的類似。當球體直徑從20 mm增至45 mm時，襯墊厚度4 mm的變化最為明顯，基圓面積從31.10 mm2增至154.10 mm2，增加率為395.50%，而相應的滑移面面積增加率較小。與跌落高度的結果相比，球體直徑有著更明顯的影響，進行簡單對比：以襯墊厚度4 mm為例，當跌落高度從200 mm增至400 mm時，基圓面積增加了30.72%；當球體直徑從20 mm增至40 mm時，基圓面積增加了305.47%。從能量角度來看，球體的重力勢能h==(π3/6)（、和分別為球體的質量、密度和直徑，為跌落高度，為重力加速度），由于能量變化與直徑是3次方關系，而與高度是線性關系，所以，對于同等比例的變化，直徑比高度的影響更大。

圖6b為能量吸收率的變化，隨著球體直徑的加，吸收率略微變大。不同襯墊厚度的變化規律與前文的分析類似。圖6c為切向能量比率的變化，切向能量比率均小于8.5%，并隨著球體直徑增大而減小。從變化比較明顯的無襯墊和襯墊厚度為4 mm的結果來看，球體直徑從20 mm增至45 mm時，切向能量比率分別從7.73%減少到4.82%和從8.35%減少到2.17%。可見，隨著球體直徑增加，碰撞過程中界面材料的應變能增多，而摩擦耗能減少。

3.4 球體材料的影響

將鋼、銅和鋁等不同材料的球體（直徑為20 mm）從高度400 mm處自由跌落到鋪設有厚度為2 mm襯墊的鋼板上，不同沖擊角工況下的結果見圖7。

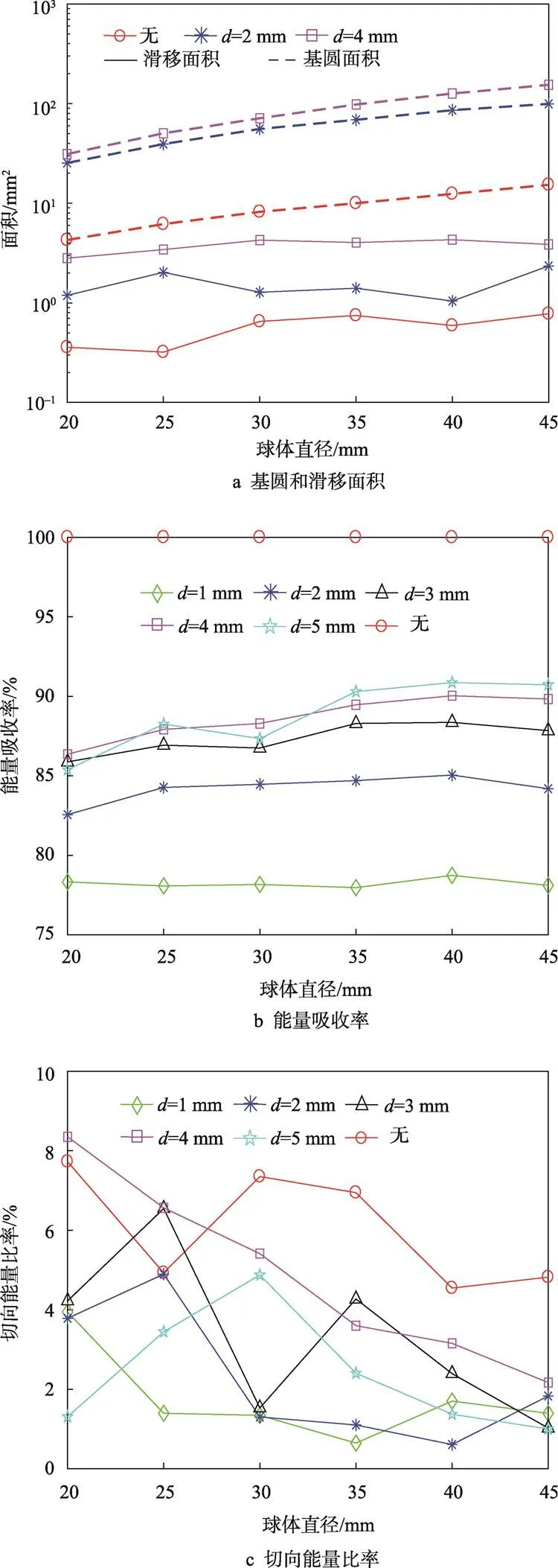
圖6 不同球體直徑下斜碰撞接觸面積和能量參量

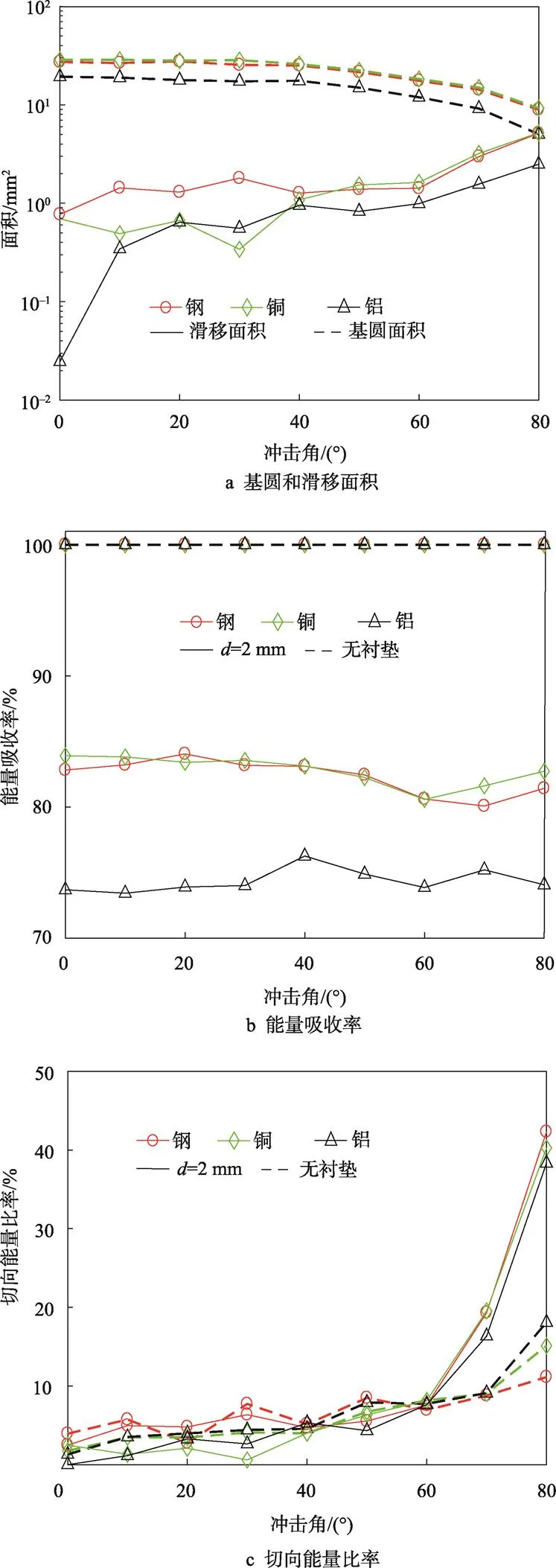
圖7 不同球體材料下斜碰撞接觸面積和能量參量

不同材料球體碰撞接觸面基圓和滑移面面積的變化，如圖7a所示，與3.1節的分析結果類似。當沖擊角小于40°時，對應的基圓面積變化均較小，銅球比鋼球的略微大些，而這兩者的基圓面積變化明顯大于鋁球的。這主要是由于材料密度的影響，銅和鋼的密度分別為8.96 g/cm3和7.93 g/cm3，大于鋁的密度2.70 g/cm3，同等體積，質量較大的球將產生更大的接觸面積。當沖擊角從40°增至80°時，基圓面積明顯下降，銅、鋼和鋁球基圓面積的下降率分別為64.29%、64.52%和71.38%。鋁球的下降率最大，這是因為鋁球的密度較小，運動狀態更容易改變。滑移面面積的變化與基圓面積的正好相反。

綠色經濟發展是一個動態的過程，其效應需要一定的時間才能反映出來。因此，指標的選擇要充分考慮到動態變化特點，選取多年數據進行動態分析。

為了便于對比，在圖7b和圖7c中描述無襯墊碰撞結果。能量吸收率的變化見圖7b，銅球和鋼球的數值比較接近，在80%～84%內變化，而鋁球的要小些，在74%左右變化。切向能量比率的變化見圖7c，當沖擊角小于60°時，能量比率緩慢增加，3種材料均在8.2%以下，無明顯區別。當沖擊角大于60°時，切向能量比率急劇增加。當沖擊角為80°時，鋼、銅和鋁球在襯墊厚度2 mm的比率分別為43.32%、40.26%和38.34%，相比之下，同等體積，質量較小的球體的切向能量比率較小。

4 結語

文中基于球體斜碰撞接觸面積研究界面處能量吸收率、傳遞率和轉換率，分析了不同因素對這些參量的影響。常見的包裝材料結構形式比橡膠的復雜，文中的分析可為其他材料的研究奠定基礎，主要結論如下。

1）利用接觸面積計算能量吸收率、傳遞率和轉換率，遵循能量守恒定律，具有可行性。

2）隨著跌落高度、球體直徑和密度增加，接觸面積和能量吸收率變大，這與接觸理論的分析結果是一致的；襯墊存在最佳吸能厚度，而沖擊角對能量吸收率的影響很小。

3）隨著沖擊角增加、球體直徑減小，法向能量比率下降，而切向的比率增加；能量轉換曲線存在一個急劇下降點，襯墊厚度越大，轉折點對應的沖擊角越小；跌落高度和材料密度對能量比率并無明顯的影響。

[1] 潘迪, 韓勇, 張坤倫, 等. 液晶電視包裝件跌落仿真及結構優化[J]. 包裝工程, 2019, 40(11): 94-99.

PAN Di, HAN Yong, ZHANG Kun-lun, et al. Drop Simulation and Structure Optimization of LCD TV Package[J]. Packaging Engineering, 2019, 40(11): 94-99.

[2] DOMéNECH-CARBó A, DOMéNECH-CASASúS C. Analysis of Microsphere Oblique Impact with Planar Surfaces Based on the Independent Friction-Restitution Approach[J]. Journal of Aerosol Science, 2020, 140: 1-3.

[3] STROPEK Z, GOACKI K. Bruise Susceptibility and Energy Dissipation Analysis in Pears under Impact Loading Conditions[J]. Postharvest Biology and Technology, 2020, 163: 1-7.

[4] STRONGE W J. Impact Mechanics[M]. Cambridge: Cambridge University Press, 2000: 86-145.

[5] BRAKE M R. An Analytical Elastic Plastic Contact Model with Strain Hardening and Frictional Effects for Normal and Oblique Impacts[J]. International Journal of Solids and Structures, 2015, 62(1): 104-123.

[6] 王慶朋, 張力, 唐志剛, 等. 粗糙結合面法向接觸的能量耗散與阻尼特性研究[J]. 振動與沖擊, 2017, 36(2): 129-133.

WANG Qing-peng, ZHANG Li, TANG Zhi-gang, et al. Energy Dissipation and Damping Characteristics Analysis on the Normal Contacts of Rough Joint Surfaces[J]. Journal of Vibration and Shock, 2017, 36(2): 129-133.

[7] MESSAADI M, KERMOUCHE G, KAPSA P. Numerical and Experimental Analysis of Dynamic Oblique Impact: Effect of Impact Angle[J]. Wear, 2015, 332-333: 1028-1034.

[8] NISHIDA M, HAYASHI K, TOYA K. Influence of Impact Angle on Size Distribution of Fragments in Hypervelocity Impacts[J]. International Journal of Impact Engineering, 2019, 128: 86-93.

[9] 謝若澤, 鐘衛洲, 黃西成, 等. 吸能包裝模型結構的沖擊響應[J]. 爆炸與沖擊, 2019, 39(10): 42-50.

XIE Ruo-ze, ZHONG Wei-zhou, HUANG Xi-cheng, et al. Impact Response of Scaled Models of an Energy-Absorbing Container[J]. Explosion and Shock Waves, 2019, 39(10): 42-50.

[10] KEY C T, ALEXANDER C S. Numerical and Experimental Evaluations of a Glass-Epoxy Composite Material under High Velocity Oblique Impacts[J]. International Journal of Impact Engineering, 2020, 137: 1-10.

[11] MAW N, BARBER J R, FAWCETT J N. The Rebound of Elastic Bodies in Oblique Impact[J]. Mechanics Research Communications, 1977, 4(1): 17-22.

[12] THORNTON C, NING Ze-min. A Theoretical Model for the Stick/Bounce Behaviour of Adhesive, Elastic- Plastic Spheres[J]. Powder Technology, 1998, 99(2): 154-162.

[13] DOMéNECH-CARBó A. Analysis of Rolling Friction Effects on Oblique Rebound by Redefining Tangential Restitution and Friction[J]. Physics of Fluids, 2019, 31(4): 1-9.

[14] 韓維, 胡海巖, 金棟平. 兩自由度振動系統的斜碰撞分析[J]. 力學學報, 2003, 35(6): 723-729.

HAN Wei, HU Hai-yan, JIN Dong-ping. Analysis of Oblique Impact of a Vibrating System of Two Degrees of Freedom[J]. Acta Mechanica Sinica, 2003, 35(6): 723-729.

[15] DONG H, MOYS M H. Experimental Study of Oblique Impacts with Initial Spin[J]. Powder Technology, 2006, 161(1): 22-31.

[16] CROSS R. Oblique Impact of a Steel Ball[J]. Powder Technology, 2019, 351: 282-290.

[17] 馮斌, 孫偉, 石林榕, 等. 收獲期馬鈴薯塊莖碰撞恢復系數測定與影響因素分析[J]. 農業工程學報, 2017, 33(13): 50-57.

FENG Bin, SUN Wei, SHI Lin-rong, et al. Determination of Restitution Coefficient of Potato Tubers Collision in Harvest and Analysis of Its Influence Factors[J]. Transactions of the Chinese Society of Agricultural Engineering, 2017, 33(13): 50-57.

[18] IRELAND P M. Impact Tribocharging of Soft Elastic Spheres[J]. Powder Technology, 2019, 348: 70-79.

Experimental Study on Energy Transfer and Conversion during Sphere Oblique Impact of Packing Materials

WANG Qing-peng1,2, LI Wei1, WANG Heng1, WANG Zhen-feng1,2, LI De-feng1, XU Guang-yin1,2

(1. School of Mechanical and Electrical Engineering, Henan Agricultural University, Zhengzhou 450002, China; 2. Henan Provincial Cold Chain Information and Equipment Laboratory for Logistics of Agricultural Products, Zhengzhou 450002, China)

The work aims to propose a calculation model of energy rate of absorption, transfer and conversion based on the geometrical characteristics of impact contact surface to solve the problems of energy changes of packing materials at interface and their quantitative characterization during sphere oblique impact. Firstly, the geometrical characteristics of contact surface of sphere oblique impact was analyzed, and the computation formula of the absorption rate, transfer rate and energy ratios at different directions was proposed through the areas of base circle and slip surface. Subsequently, the test device of oblique impact of sphere free falling was built. Then, the effects of the impact angle, cushion thickness, drop height, sphere diameter and material density on the energy parameters were analyzed. It was feasible to calculate the energy absorption rate and conversion rate by impact contact area, following the law of conservation of energy. The energy absorption rate was nearly above 75%, becoming greater with increasing drop height, sphere diameter and material density, while the effect of impact angle was slight. The normal rate of energy conversion decreased with the increasing impact angle and the decreasing sphere diameter, but the tangential energy ratio was opposite, and the falling height and density had no obvious effect on the energy ratio. Under given working conditions, the optimum energy absorption thickness of the cushion was 4 mm. This analysis can be conducive to studying the energy change and contact characteristics at the interface of packing materials.

packing materials; oblique impact; contact area; energy absorption; transfer and conversion

O313.4

A

1001-3563(2022)17-0093-09

10.19554/j.cnki.1001-3563.2022.17.012

2021–11–18

中國博士后基金項目（204225）；河南省級科技攻關項目（202102110127）；河南省高等學校重點科研項目（20B210010）；河南農業大學科研啟動項目（30500461）

王慶朋（1987—），男，博士，講師、碩導，主要研究方向為農產品物流測試技術。

責任編輯：曾鈺嬋