混合潤滑下粗糙表面的接觸剛度研究*

馬 歡 景 卉

(1.西安交通大學航天航空學院 陜西西安 710048；2.蘭州大學管理學院 甘肅蘭州 730000)

機械結合面是機械裝備中各零部件之間的接觸表面，對于各種高精密設備，結合面的接觸剛度對設備的精度和性能有著重要影響。通常情況下，為了減少磨損，提高設備使用壽命，結合面往往都處于潤滑狀態[1]。機械結合面一般可以等效為2個粗糙表面之間的接觸，因此，潤滑狀態下的粗糙表面間接觸剛度的研究意義重大。

自經典赫茲接觸[2]被提出以來，國內外學者對粗糙表面之間的接觸進行了廣泛研究[3-10]。其中以GREENWOOD-WILLIAMSON(G-W)模型[3]為代表的統計學接觸模型和Persson接觸理論[5]為代表的分形接觸模型被廣泛認可。在G-W模型中，兩個粗糙面之間的接觸往往等效為一個剛性平面和一個彈性粗糙表面之間的接觸，粗糙面由曲率相同的球面組成，且其高度服從高斯分布。但由于粗糙表面的多尺度特征，統計學模型會受儀器分辨率的影響。為了更好地表征粗糙表面的多尺度特征，PERSSON[5]通過引入放大率概念，發展了一種基于壓力擴散方法的隨機粗糙表面接觸理論。然而，上述模型僅僅考慮了干接觸條件下的粗糙表面接觸，沒有考慮潤滑對接觸特性的影響。

在實際工業應用中，各種齒輪、軸承等機械系統以混合潤滑接觸方式工作，以減少摩擦或磨損。超聲反射法是實驗測量界面接觸剛度的主要手段。GONZALEZ-VALADEZ等[11]利用超聲技術測量了潤滑界面接觸剛度。然而，基于超聲反射法測得的潤滑粗糙界面的接觸剛度遠大于實際值[12]。因此，研究一種理論模型預測混合潤滑狀態下的接觸剛度是非常必要的。

本文作者提出了一個混合潤滑狀態下粗糙表面的接觸剛度等效薄層模型，研究了不同實際接觸面積下，表面形貌和潤滑劑對法向接觸剛度的影響，為研究混合潤滑狀態下粗糙界面的接觸特性提供了理論基礎。

1 混合潤滑狀態下的接觸剛度模型

1.1 模型描述

潤滑狀態下的粗糙接觸界面由粗糙峰和周圍的潤滑劑組成，如圖1所示。對于混合潤滑粗糙界面，界面剛度由固體剛度和潤滑劑剛度2部分組成，且其剛度關系符合彈簧并聯準則，即

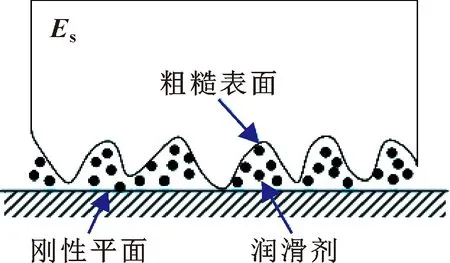
圖1 混合潤滑狀態下的粗糙界面

Kn=Ks+Kl

(1)

式中：Kn為潤滑狀態下粗糙界面總接觸剛度；Ks為固體剛度；Kl為潤滑劑剛度。

對于彈性潤滑界面，假設等效薄層與接觸固體和平坦剛性表面剛性連接，如圖2所示。因此，單位標稱接觸面積的法向接觸剛度[12]可以表示為

圖2 混合潤滑接觸等效薄層示意

(2)

式中:H0為等效薄層厚度，基于粗糙統計理論，H0一般取值為3倍的均方根粗糙度[13];E0為等效彈性模量,可表示為

E0=φ1Es+φ2Bl

(3)

式中:Es為固體的彈性模量;Bl為潤滑劑的體積模量;φ1、φ2分別為等效彈性模量中固體和潤滑劑的貢獻比例，并滿足

φ1+φ2=1

(4)

因此，固體剛度和潤滑劑剛度可分別表示為

(5)

(6)

1.2 潤滑接觸剛度表達式

文中推導潤滑接觸狀態下界面接觸剛度的表達式。首先，基于WANG等[8]提出的干接觸時粗糙表面增量接觸模型推導得到單位標稱面積固體接觸剛度表達式為

(7)

式中：A0為標稱接觸面積；A(z)和N(z)分別為當粗糙界面分離為z時，粗糙表面的實際接觸面積和等效圓斑數量。

將式(7)代入式(5)可得固體部分的貢獻比例φ1為

(8)

將式(8)代入式(4)可得潤滑劑部分的貢獻比例φ2為

(9)

將式(8)和式(9)代入式(3)可得潤滑接觸等效彈性模量E0為

(10)

將式(10)代入式(2)可得潤滑接觸界面法向剛度Kn為

(11)

將式(9)代入式(6)可得潤滑劑剛度Kl為

(12)

盡管固體的彈性模量遠遠大于潤滑劑的體積模量，潤滑劑對剛度的貢獻也不可忽略，因為在粗糙峰初始接觸時，固體的貢獻比例接近于0，而潤滑劑貢獻比例接近于1。

2 結果和討論

2.1 混合潤滑狀態下接觸剛度

根據1.2節中潤滑接觸狀態下界面接觸剛度模型，只需粗糙表面的高度節點信息，便可預測混合潤滑狀態下接觸剛度的演化。首先，通過PSD法在MATLAB中生成一個100 μm×100 μm的隨機粗糙表面，其節點高度信息如圖3所示。粗糙表面的具體參數為：σ=3 μm，Es=115.4 GPa，Bl=1.45 GPa，H=0.8，ν=0.3，其中H為赫斯特指數，ν為泊松比。基于以上信息，利用等效薄層模型數值求解混合潤滑狀態下接觸剛度。如圖4所示，隨著實際接觸面積的增大，接觸剛度近似線性增加，與G-W模型[3]和Persson接觸理論[5]所得到的線性關系一致。對于相同的實際接觸面積，有潤滑劑界面的接觸剛度大于無潤滑劑界面的接觸剛度。固體和潤滑劑分別對總接觸剛度的貢獻比例隨著實際接觸面積增大的變化規律如圖5所示。初始接觸時φ2>φ1，潤滑劑作用占主導地位，但隨著實際接觸面積的增大，固體接觸剛度逐漸超過潤滑劑接觸剛度占據主導地位。這說明在小載荷下，潤滑劑的接觸剛度對于總接觸剛度具有重要意義。

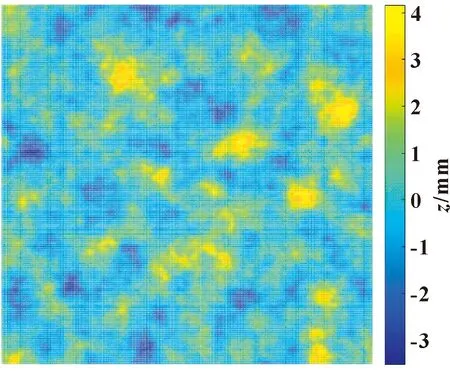
圖3 粗糙表面形貌

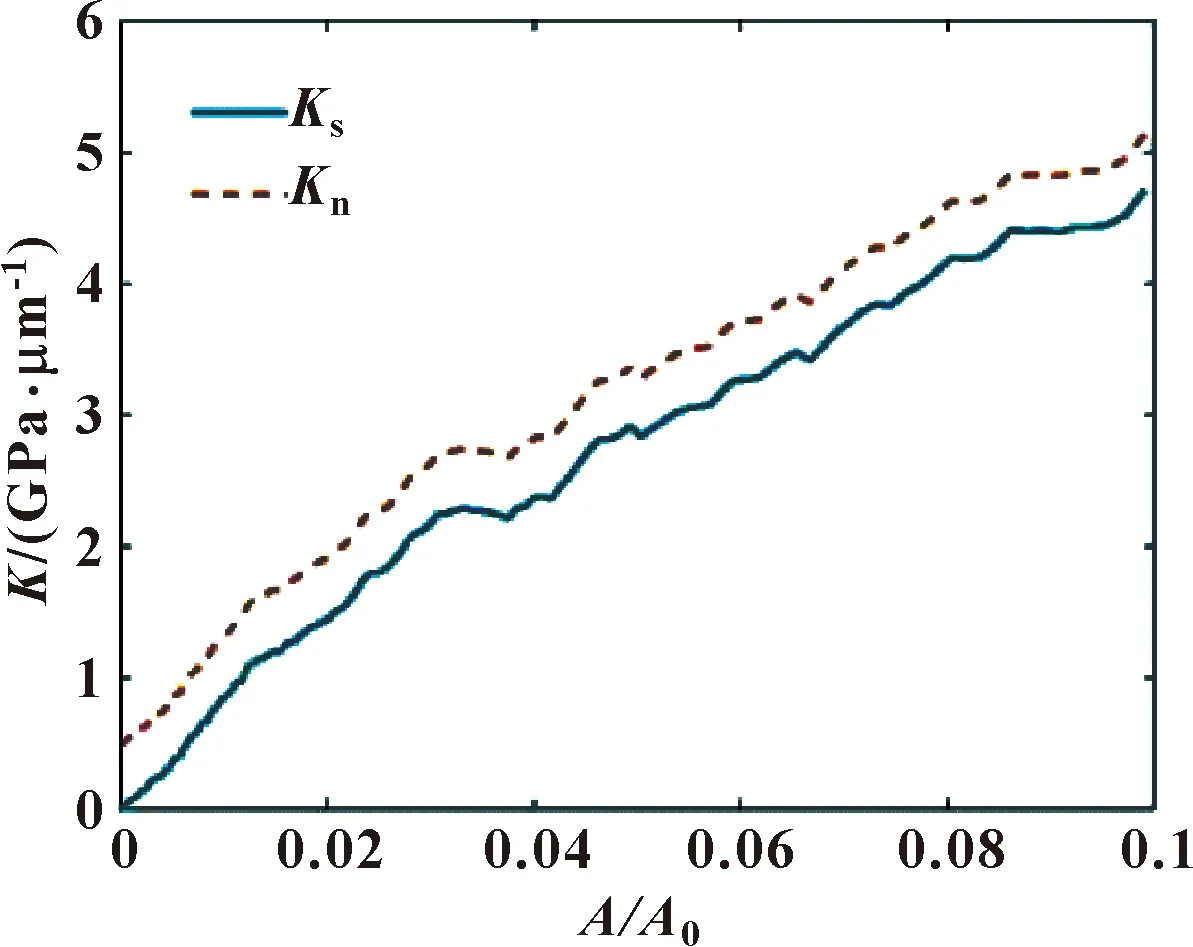
圖4 有無潤滑劑條件下接觸剛度與面積比的關系

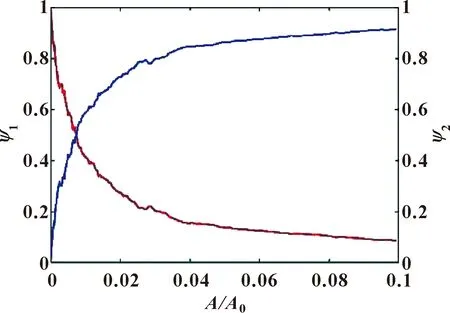
圖5 固體和潤滑劑的貢獻比例與面積比的關系

2.2 潤滑劑類型對混合潤滑接觸剛度的影響

為了研究潤滑劑類型對混合潤滑接觸剛度的影響，文中比較了2種不同類型的潤滑劑對接觸剛度的影響。潤滑劑在環境壓力下的體積模量為

Bl=Bl0e-βkT

(13)

式中：Bl0為環境壓力下溫度為0 K時的體積模量；βk為泰特-杜利特爾常數；T為絕對溫度。

表1列出了分析中使用的2種潤滑劑的相關參數[14]。

表1 環境壓力下潤滑劑的參數[14]

圖6(a)和圖6(b)示出了在分別使用T9油和甘油2種潤滑劑下，總接觸剛度、固體接觸剛度和潤滑劑接觸剛度隨實際接觸面積的變化規律。可知，總接觸剛度、固體接觸剛度隨著實際接觸面積的增大而增大，且總接觸剛度總是大于固體接觸剛度，而潤滑劑接觸剛度基本保持不變，并且在小載荷下潤滑劑接觸剛度大于固體接觸剛度。通過對比2種不同的潤滑劑，可以發現潤滑劑的體積模量越大，混合潤滑接觸剛度增大越明顯，潤滑劑接觸剛度占主導地位的范圍也越大，這與實際情況是一致的。

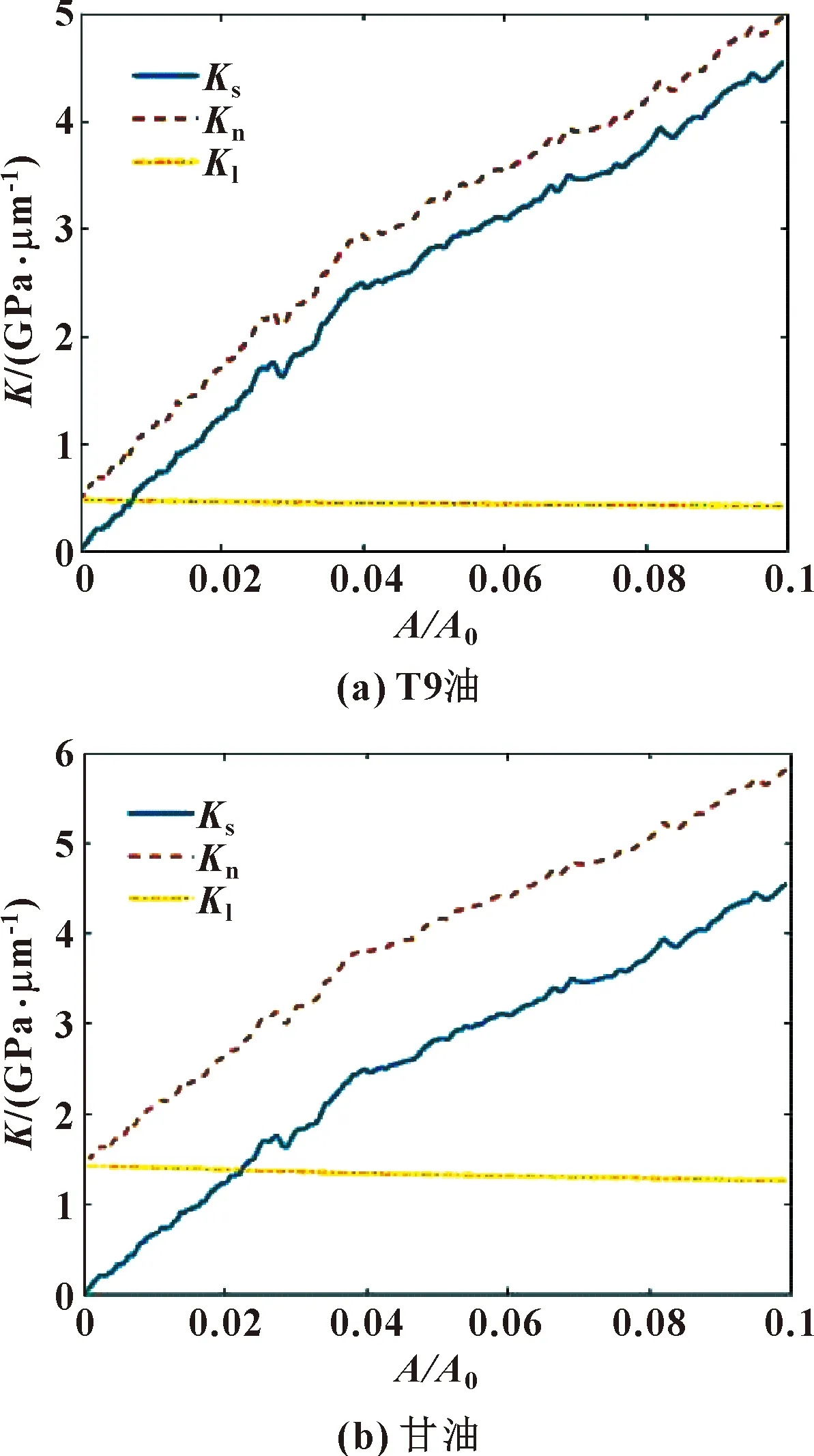
圖6 不同潤滑劑下法向接觸剛度與面積比的關系

2.3 表面形貌對混合潤滑接觸剛度的影響

為了探究表面形貌對混合潤滑接觸剛度的影響，通過PSD法生成了3種不同粗糙度的隨機粗糙表面，具體參數見表2。表面形貌對T9油潤滑界面接觸剛度的影響如圖7所示，不同粗糙度的潤滑界面的法向剛度均隨著實際接觸面積的增大而增大。在實際接觸面積相同的情況下，更光滑的表面會產生更大的接觸剛度。

表2 不同表面形貌的具體參數

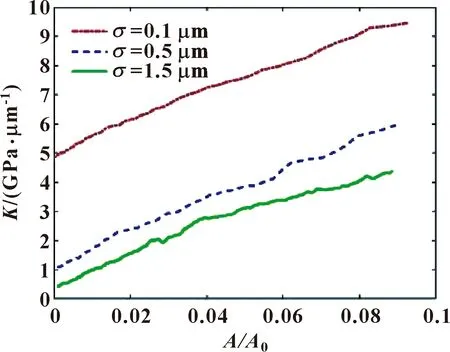
圖7 表面形貌對混合潤滑接觸剛度的影響

3 模型對比

為了驗證文中提出的接觸剛度模型的準確性，將文中模型與文獻[13]的模型進行了比較。選用的參數為σ=2.04 μm，Es=115.4 GPa，Bl=1.45 GPa，H=0.7，ν=0.3。如圖8所示，當實際接觸面積相同時，文中模型的預測結果與文獻[13]的模型的計算結果具有良好的一致性，證明了文中提出的混合潤滑狀態下粗糙界面的法向接觸剛度模型的合理性與有效性。與現有模型相比，文中模型的創新之處在于只需要提供粗糙表面的高度信息，便可以簡單準確地預測干接觸和潤滑接觸時接觸剛度隨實際接觸面積的演化。

圖8 不同模型法向接觸剛度與面積比的關系

4 結論

通過提出一種等效薄層模型解決混合潤滑狀態下粗糙界面接觸剛度的預測問題，將接觸界面的總剛度等效為固體接觸剛度和潤滑劑接觸剛度之和，從理論上估算了混合潤滑法向接觸剛度與實際接觸面積的關系。主要研究結果如下：

(1)粗糙界面的法向接觸剛度隨法向載荷的增加而增加，且混合潤滑狀態下的接觸剛度大于干接觸條件下的接觸剛度。

(2)在初始接觸時，粗糙界面的法向剛度主要受潤滑劑性能影響，隨著實際接觸面積的增大，固體剛度逐漸占據主導地位，表面形貌對法向接觸剛度的影響變得更加明顯，潤滑劑的影響越來越小。

(3)建立的模型的預測結果與經典模型計算結果具有良好的一致性，驗證了建立的模型的正確性。