基于勻壓和阻尼的空氣靜壓軸承靜態特性研究*
馬 偉 孔祥龍 徐 毅 李文龍 王旭生 牟旭娜
(上海衛星工程研究所 上海 201108)
在精密超精密制造和測量裝備領域中,空氣靜壓軸承由于其非接觸工作、運動精度高和摩擦磨損小等優點而獲得廣泛應用。尤其在半導體產業裝備中,在有限承載面積下具備高承載力、高剛度和高自激穩定性的空氣靜壓軸承成為空氣軸承研究熱點和應用難點。
為了提高空氣靜壓軸承的承載能力和剛度,可通過提高供氣壓力、增加均壓槽[1-2]、增加節流孔數[3]和選擇合適節流方式等方法,但提高供氣壓力和增設均壓槽會造成空氣靜壓軸承自激穩定性[4]降低,嚴重時會發生氣錘自激振動現象;而增加節流孔數量會造成流量的顯著增加,且承載力存在上限值。對于提高空氣靜壓軸承剛度,亦可采用閉式結構[5]、微孔節流形式[5-9],引入柔性部件[10]以及采用主動節流控制方式[11]以獲得高剛度空氣靜壓軸承,但其帶來結構的復雜,對空氣靜壓軸承的應用帶來不便。上述研究均未考慮其對空氣靜壓軸承自激穩定特性的影響,實際上在參數選擇不當時會引起空氣靜壓軸承的氣錘自激振動現象。空氣靜壓軸承氣錘自激穩定特性與承載區內的壓力波動有關[12-13],且可用空氣靜壓軸承的阻尼特性表征[14],故研究空氣靜壓軸承的阻尼特性成為空氣靜壓軸承動態穩定特性研究的熱點問題。借鑒空氣彈簧的高阻尼特性而在空氣靜壓軸承中引入其形式可顯著改善空氣靜壓軸承的阻尼特性[15]。但若結構設計不合理,會由于空氣靜壓軸承的容積效應加劇而誘發氣錘自激振動。增加承載面積同樣可提高其阻尼特性,但在結構受限的場合不適用,且目前的研究均未考慮承載面積對空氣靜壓軸承特性的影響。因此有必要針對在有限承載面積下兼顧承載力、剛度和自激穩定特性的空氣靜壓軸承進行研究。
本文作者提出基于虛擬均壓和被動阻尼空氣靜壓軸承設計方法,據此設計一種在有限承載面積下具備高承載力、高剛度和高自激穩定性的空氣靜壓軸承,并在此基礎上通過數值分析和實驗驗證方法以研究供氣壓力、均壓槽尺寸和阻尼孔數量對其靜態特性的影響。研究結果用于指導空氣靜壓軸承設計,拓展空氣靜壓軸承應用范圍。
1 理論分析
1.1 雷諾方程改進
一般化雷諾方程為
(1)
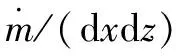
在空氣靜壓靜態特性分析時對于含有均壓槽的雷諾方程[16]為
(2)
1.2 軸承設計及有限元分析
設計一般形式矩形平面空氣靜壓止推軸承,其外形尺寸為127 mm×55 mm,節流孔間距為10 mm,節流孔數量為16。其結構如圖1所示。為了獲得高承載和高剛度的性能要求,在承載面增設環狀均壓槽,由均壓槽引導氣流垂直于邊緣流至周圍環境,使得流場分布更規則,同時在環狀均壓槽所圍成的區域內形成均壓區,構成虛擬均壓。但均壓槽在提高承載力和剛度的同時會增加容積效應而加劇發生氣錘自激不穩定振動的風險。為了改善其穩定性,在虛擬均壓區內引入陣列阻尼孔,使得供氣通道,阻尼孔和虛擬均壓區構成類似空氣彈簧結構,通過提高空氣靜壓軸承的阻尼特性來改善其自激穩定特性。設計的含環狀均壓槽和陣列阻尼孔的矩形平面空氣靜壓止推軸承如圖2和圖3所示。設計的空氣靜壓軸承結構參數如表1所示。

表1 氣體靜壓止推軸承結構參數
對設計的空氣靜壓軸承的靜態特性進行數值計算分析。首先分析空氣靜壓軸承模型,考慮結構的對稱性,對結構的1/4進行有限元離散化處理以簡化分析復雜性。最終網格劃分如圖4所示。
利用上節的含均壓槽的雷諾方程離散化處理并通過MatLab數值求解工具計算空氣靜壓軸承承載區域的壓力分布。承載區域內的壓力分布對承載面積積分即可獲得承載力,進而可得到空氣靜壓軸承剛度。采用有限元方法分析時,網格密度的高低對分析結果有較大影響。因此在進行氣體靜壓止推軸承靜態特性規律分析前,需選擇滿足分析精度要求的網格密度。網格密度對氣體靜壓平面止推軸承靜態承載能力和流量的影響如圖5所示。
由圖5可知,隨著網格數量的增加,承載力和體積流量呈近似雙曲線規律變化。當網格數量為1 500時,與更高網格密度相比,分析結果變化控制在2%以內,在該網格密度下具有最佳的分析精度和分析效率。因此,在氣體靜壓止推軸承靜態特性的后續分析中選擇網格密度1 500。
2 理論結果及分析
2.1 壓力分布及承載力分析
對上述結構在供氣壓力5 MPa、氣膜厚度10 μm的條件下,通過有限元數值求解方法分析空氣靜壓軸承承載區的壓力分布,結果如圖6和圖7所示。
由圖6和圖7可看出,在初始空氣靜壓軸承的承載區域內,壓力經節流孔后存在較大壓降,而在改進空氣靜壓軸承的承載區內在中心可看到幾乎恒定的高壓分布,在邊緣迅速下降為環境壓力,同時可見節流孔入口處的壓力尖峰。因此,借助有限元方法可以獲得承載面的結構特征在壓力分布上的表征。2種結構在承載力和剛度上的對比如圖8和圖9所示。
由圖8和圖9可以看出,相比初始空氣靜壓軸承,改進空氣靜壓軸承的最大承載力由2 020.8 N提升到2 906.56 N,提高了43.4%,最高剛度由105.75 N/μm提高到159.97 N/μm,提高了51.3%。因此改進結構在靜態特性上有了顯著提高。
2.2 供氣壓力對靜態特性的影響
分析不同供氣壓力對空氣靜壓軸承靜態特性的影響,分析結果如圖10和圖11所示。可看出,隨著供氣壓力的增加,在相同氣膜厚度下承載力單調增加,在同一供氣壓力下隨著氣膜厚度的增加,承載力呈單調減小趨勢;隨著供氣壓力的增加空氣靜壓軸承的剛度呈單調增加,且最大剛度具有左移(向小間隙方向移動)趨勢。
2.3 節流孔徑對靜態特性的影響
圖12和圖13所示為節流孔徑對空氣靜壓軸承靜態特性的影響。可看出,在相同氣膜厚度下,隨著孔徑減小,最大承載力不變,但承載力下降幅度增大,且最大剛度值提高并向小氣膜方向移動,同時流量顯著減小。經分析發現空氣靜壓軸承的流量與節流孔徑的立方成正比,因此節流孔徑對空氣靜壓軸承流量影響最大。通過分析空氣靜壓軸承承載力與剛度的關系可發現,小節流孔徑具有在大的承載范圍存在高剛度的特點,因此減小節流孔徑可在小氣膜間隙下獲得小流量和高剛度的特性。但此時會對空氣靜壓軸承氣浮面的面形精度提出較高要求,從而增加加工和裝配難度。
2.4 阻尼孔數對靜態特性的影響
圖14和圖15所示為阻尼孔數對空氣靜壓軸承靜態特性的影響。可以看出,阻尼孔的增加帶來剛度略有下降,流量有所增加,但如果氣隙小則影響不大。對于空氣靜壓軸承由于缺少阻尼和小的預緊力而產生自激振動穩定性問題,阻尼孔可在不造成流量增加過大的情況下有效地抑制軸承的自激振動情況的發生。
3 實驗驗證
為了對理論分析結果進行驗證,制作了空氣靜壓軸承,其外形尺寸為55 mm×127 mm,節流孔徑為0.2 mm,節流孔數為22,邊距為10 mm,阻尼孔數為10,阻尼孔孔徑為0.2 mm,均壓槽數量為18,均壓槽尺寸為12 mm×1 mm×0.02 mm。其結構如圖16所示。
實驗采用電動缸施加外部載荷,采用力傳感器檢測實際載荷值,在空氣靜壓軸承和力傳感器之間采用球形解耦以避免由于施加載荷的偏載對實驗造成的影響。在空氣靜壓軸承上采用2個電感位移傳感器來檢測空氣靜壓軸承與花崗石氣浮面之間的相對距離,即氣膜厚度。為了避免管路對供氣壓力造成的影響,將氣壓傳感器盡可能靠近空氣靜壓軸承。搭建的實驗裝置如圖17所示。
對空氣靜壓軸承在不同阻尼孔下進行靜態特性實驗測試,實驗在相同條件下進行了16次重復實驗以減小隨機誤差對實驗結果的影響,實驗與理論對比如圖18和圖19所示。
由圖18和圖19可以看出,實驗測試與理論分析趨勢一致,且通過對實驗結果的數據擬合,發現實驗結果與理論分析的差值在6%內,在允許的誤差范圍內,故說明該分析模型的可行性。同時實驗發現,在阻尼孔為10個時,空氣靜壓軸承結構在16~22 μm之間發生了氣錘自激振動,當阻尼孔為0時,空氣靜壓軸承結構在13~23 μm之間發生了氣錘自激振動。由兩者的對比可發現,增加阻尼孔數量可改善空氣靜壓軸承的自激振動穩定特性。
4 結論
針對在有限承載面積上高承載、高剛度和高自激振動穩定特性的性能需求,采用基于虛擬均壓和被動阻尼的方法設計了含環布均壓槽和陣列阻尼孔的矩形平面空氣靜壓止推軸承,并從雷諾方程出發推導了含均壓槽的雷諾方程,在此基礎上對雷諾方程離散化,利用有限元方法對設計的空氣靜壓軸承結構分析,研究了供氣壓力、節流孔徑、阻尼孔數量和均壓槽對其靜態特性的影響并進行了實驗驗證。研究結果表明:
(1)與常規空氣靜壓軸承結構相比,在供氣壓力為0.5 MPa時,含環布均壓槽和陣列阻尼孔的空氣靜壓軸承最高承載力由2 020.8 N提升到2 906.56 N,提高了43.4%,最高剛度由105.75 N/μm提高到159.97 N/μm,提高了51.3%,其靜態特性得到顯著提高。因此設計和加工的空氣靜壓軸承具有高承載、高剛度和高自激振動穩定性的綜合特性。
(2)減小阻尼孔數量、減小節流孔徑、提高供氣壓力和增設均壓槽可獲得剛度最佳特性;增加阻尼孔數量、減小節流孔徑、提高供氣壓力和增設均壓槽可獲得最佳靜態特性和動態穩定特性的綜合性能。
(3)通過實驗對比驗證,說明該有限元數值求解方法有效可行,可用于對該結構的靜態特性分析,且發現通過均壓槽和阻尼孔的組合,可在盡量不改變空氣靜壓軸承承載力和剛度的前提下,提高其自激穩定特性。

