傳統譜聚類算法概述

許洪瑋

（廣東工業大學信息工程學院，廣東廣州 510006）

聚類算法是要將數據集中具有相似性的數據劃分為一類，而將不相似的數據劃分為不同類，最終實現將數據集劃分為若干類。其主要過程包括確定樣本數據、獲取特征、計算特征值、計算相似度、評估聚類結果的有效性等步驟。聚類算法可以按照聚類原理分為：劃分方法、層次方法、基于密度的方法、基于網格的方法、基于模型的方法、基于圖論的方法等。

譜聚類算法（Spectral Clustering Algorithm）與K-means算法、EM算法和模糊C均值聚類算法（Fuzzy C-mean Clustering,FCM）等傳統的聚類算法不同，不需要聚類對象具有凸球形或其他特定形狀，就能在任意形狀的樣本空間上實現聚類。譜聚類算法的思想源自譜圖劃分理論[1]，該算法的核心思想是：計算樣本數據集所描述成數據點的相似度矩陣，通過特征分解，計算矩陣的特征值和特征向量（也就是譜信息），然后選擇合適的特征向量作為數據的低維空間描述，之后對選擇的特征向量應用K-means等方法進行聚類，聚類的結果最后映射回原數據空間。譜聚類算法是一種點對聚類算法，其本質是用圖的最優劃分思想處理聚類問題，解決了高維特征向量的奇異問題，因為它只和數據集的規模有關，而與數據集的維數無關。

以下幾個方面，是譜聚類算法相比傳統聚類算法的優點：

（1）譜聚類算法不對數據集的全局結構進行假設，其思想簡單、實現方便；

（2）譜聚類算法是一種點對聚類方法，它與數據的特征向量維數無關，只與數據的個數有關，可用于解決高特征向量維數的奇異性問題；

（3）譜聚類算法可以通過特征向量分解，在放松了的連續域中獲得全局最優解。

因此，譜聚類算法成為解決實際應用問題的新方法，可應用于圖像分割、視頻分割、語音識別、文本挖掘等研究領域的問題解決。盡管譜聚類方法在一些問題的解決上取得了不錯的效果，但還有許多值得深入研究的問題。

本文主要對一些基本算法進行概述，包括：圖譜和譜分解的基本概念、傳統譜聚類算法的概述、基于密度聚類算法概述和評價指標Rand Index。

1 圖的譜及圖的譜分解概述

譜圖劃分理論是譜聚類算法的思想來源，圖的譜分布與圖的結構之間的對應關系是近年來興起的相當活躍的研究課題，其中特征值及相關概念是研究的集中方向。下面簡要介紹譜的基本概念[2]。

圖的表示方法為G=(V,E)，其中V={v1,v2,...,vn}是頂點或點的集合，E={e1,e2,...,em}是連接任意兩個點的邊的集合，頂點的個數n=|V|，邊的個數m=|E|。如果連接頂點u、v的邊euv的值是無窮的，則稱頂點u、v是不相鄰的，否則是相鄰的；如果邊e1和e2有一個共同的頂點，則稱邊e1和e2是相鄰的，否則是不相鄰的。以頂點v為端點的邊數稱為頂點v的度，記為dv。

如果兩個頂點之間的邊數不止一條，則稱為多重邊；如果一條邊的兩個頂點是相同的，則稱為邊的環。不含有多重邊和環的圖稱為簡單圖，含有多重邊的圖稱為多重圖。每一對頂點間都有邊相連的無向簡單圖稱為完全圖。本文所討論的圖全部都是完全圖。

記A(G)表示圖G的鄰接矩陣，有如下的定義：

定義（1）圖G的特征值就是對應鄰接矩陣A(G)的特征值，用λi(i=1,...,n)表示。

定 義（2）圖G的n個 特征值λi(i=1,...,n)的序 列（λ1≥λ2≥...≥λn）稱為圖G的譜。

定義（3）圖G的最大特征值λi稱為圖G的譜半徑。

定義（4）圖G的拉普拉斯特征值就是拉普拉斯矩陣L(G)的特征值。

拉普拉斯矩陣L(G)可表示為：L(G)=D(G)-A(G)，其中D(G)是圖G的度矩陣，A(G)是圖G的鄰接矩陣。

圖的特征值是圖的同構不變量，是圖論的一個重要研究課題，而我們希望通過譜方法來實現對圖的描述。下面簡要介紹圖的譜分析與譜分解。

通過計算圖的鄰接矩陣的模可以得到圖的譜特征，我們以特征值的次序來決定特征向量的次序。

如果用鄰接矩陣的特征值來構成圖G的譜特征，那么圖G的向量B可表示為：

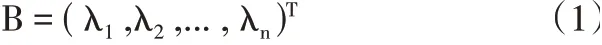
其中λ1≥λ2≥...≥λn，這一向量就表示了圖G的譜。

如果用拉普拉斯矩陣的特征值來構成譜特征，那么圖的向量B可表示為：

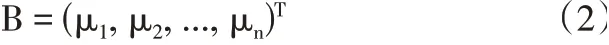
其中μ1≥μ2≥...≥μn，這一向量表示圖G的拉普拉斯。

圖的譜方法是通過圖的譜特征向量來表示圖的結構信息，這樣，一旦獲得圖的特征向量，那么一張圖就可以在特征空間上表示為一組數據，這就成為進一步處理圖數據的基礎。

圖的譜方法主要有兩個方面的優點。第一：計算復雜度較低。因為圖的譜方法可以只選取部分有效的特征來表達圖的信息，這樣就不用對圖本身進行計算，其計算復雜就被大大降低了。第二：可以用于表達海量數據的圖。海量數據的圖需要用一個好的數學表達式才能很好地表達，而尋找一個好的數學表達式往往是非常苦難的，但圖的譜方法就可以實現這種表達。

圖的譜方法自身也存在一些不足。因為選取的譜特征是有限的，這樣就不能完整地表達圖的全部結構信息，從而造成計算精確度的不夠；另外可能會出現不同的圖但它們的譜特征表達是一樣的，也就是一譜多圖的情況。

2 傳統譜聚類算法概述

譜聚類（Spectral Clustering）是基于圖論的方法把聚類問題轉換為組合優化問題，具體來說，就是將數據集表示成一個圖中所有頂點的集合，用圖相應的邊的權重表示數據之間的相似度，這樣就可以利用圖論和圖形學的原理進行分析并實現數據聚類。

若把圖中的頂點V表示成數據集中的每一個樣本，連接頂點間的邊E上的權重值W相應表示成樣本數據間的相似度，這樣就可以用無向加權圖G=(V,E,W)表示整個數據集及數據樣本間的關系。因此，可以應用圖的劃分方法解決樣本數據集的聚類問題。圖論的最優劃分理論，就是使得被劃分成的子圖內部相似度盡可能大，而劃分成的若干子圖之間相似度盡可能小[3]。圖劃分準則常用的有：規范割集、比例割集、平均割集、最小割集以及最小最大割集等劃分準則。由于圖劃分問題的本質是組合問題，其最優解求解是一個NP難題，可以通過相似度矩陣或拉普拉斯(Laplacian)矩陣的譜分解方式來解決，這種處理方法統稱為譜聚類。

譜聚類算法根據不同的圖劃分準則有不同的具體實現方法，下面是由Andrew Y.Ng[4]提出的譜聚類算法。

如果要將樣本空間上的數據集S={s1,...,sn}，劃分成k個子集（類），則具體實現步驟為：

（1）構造數據集S的相似度矩陣A，矩陣A的構造公式為：

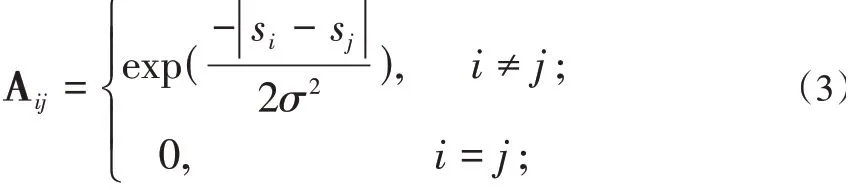
（2）對角矩陣D的第（i,i）個元素的值是矩陣A的第i行全部元素的累加和，這樣就可構造矩陣L，其計算公式為：

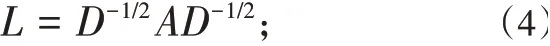
（3）計算矩陣L的特征值和特征向量，x1,x2,...,xk是最大的k個特征值所對應的特征向量，可得到n行k列的矩陣X，X=[x1x2...xk]；

（4）將矩陣X歸一化為矩陣Y，歸一化公式為：

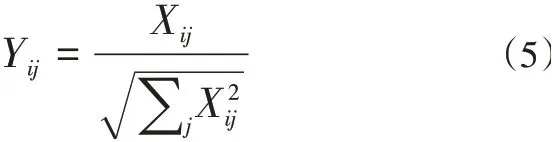
（5）對矩陣Y使用K-means算法進行分類，矩陣Y的第i行對應數據集S的第i個數據Si;

（6）矩陣Y的第i行所屬的類，就是數據集S中的數據si所屬的類，這樣就完成了對數據集的分類。

這里，尺度函數σ2是敏感參數，控制著兩個數據點之間歐氏距離的衰減程度，也直接影響著隨后的聚類效果。

譜聚類算法雖然能在一些數據集上取得較好的聚類結果如環形數據集，但對于分布比較復雜的數據集，如螺旋形數據集，該算法的聚類結果就差強人意了。這是因為譜聚類算法是通過高斯核函數來表示數據間的相似度關系，也就是在新的空間對原始的數據關系，歐氏距離關系，重新建立起映射關系，而這種映射關系只對簡單的空間分布有效，而不能正確反映空間分布比較復雜的數據關系。鑒于該算法的不足之處，研究者們不斷提出了新的改進方法。

3 DBSCAN聚類算法概述

DBSCAN[5]聚類算法是由Martin Ester等人在1996年提出的，該算法是典型的密度聚類算法，通過高密度連通性來快速發現任意形狀的類，并同時排除噪聲的干擾。

DBSCAN算法的核心參數有最小半徑Eps和最少對象數目MintPts，就是在其規定半徑Eps范圍內，所包含的數據點數不能少于給定的數目MintPts。DBSCAN算法定義了密度可達的概念，是在一個類能夠被其中任意一個核心對象點所確定的前提下，劃分出數據集的各個類的。首先，選中數據集P中的任意對象點m，查找符合Eps和MinPts條件并從對象點m密度可達的所有對象點。如果對象點m是核心點，則根據算法可以確定一個類；如果對象點m是邊界點，且點m無法密度到達其他數據點，則點m被暫時標注為噪聲點。然后，算法選取下一個數據點，并按同樣的方法進行。

DBSCAN算法步驟：

（1）輸入參數值Eps和MinPts；

（2）選取數據集中的任意一個點m，對其進行區域查詢；

（3）如果點m是核心點，則查找從m點密度可達的所有點，并形成一個類；

（4）否則，點m被暫時標注為噪聲點；

選取下一個數據點，重復步驟（2）到（4），直到處理完數據集中的所有點。

由于DBSCAN算法的參數Eps和MinPts是全局參數，比較難以確定，都必須靠先驗知識來設定，而且這兩個參數直接影響著算法的聚類性能，這樣就可能導致部分密度小的聚類被處理為噪聲；而對于邊界點，若該點附近密度較大就會形成單連通，出現錯誤分類結果。

4 聚類性能的評價指標

聚類算法的最終結果是實現數據集的劃分，而聚類結果的好壞需要進行有效性和質量評價。聚類質量的評價方法可以分為內部度量、外部度量和相對度量三類，并且每種度量方法有不同的計算方式。這里對外部度量方法中的一種計算方式——Rand Index[6]進行介紹。

Rand Index是由Milligan和Cooper提出的一種聚類質量評價指標，用于衡量聚類結果與數據的外部標準類之間的一致程度。

對于數據集X={x1,x2,...,xn}，假設S={s1,s2,...,sk}和R={r1,r2,...,rk}是數據集X的兩種不同劃分，其中S是外部標準劃分類，而R是算法的聚類結果。那么Rand Index的計算公式如下：

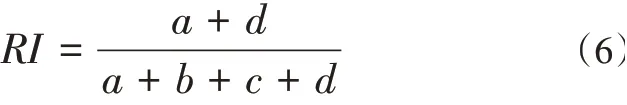
公式(6)中a表示S和R中都屬于相同類的個數，b表示屬于S中一類而不屬于R中同一類的個數，c表示屬于R中同一類而不屬于S中同一類的個數，d表示都不屬于S和R中同一類的個數。a和d反映了兩種劃分的一致性，而b和c放映了不一致性。

Rand Index的數值在[0,1]的區間內，其值越大，則表示兩種劃分的一致性就越高，當兩種劃分完全一致時，Rand Index取值為1。

5 結語

近年來，譜聚類算法成為聚類算法的熱門研究課題，也不斷涌出新算法和新研究成果。該算法可以很好地應用于解決具有非凸分布的實際問題，而如何構建一個正確反映數據間關系的相似度矩陣，是譜聚類算法研究的重點難點。希望本文對傳統譜聚類算法的介紹可以對初學者提供初步的學習借鑒。