柵格環境下機器人路徑的復合啟發蟻群規劃

龍珊珊，高 倩，高曼曼

（石家莊理工職業學院，河北 石家莊 050000）

1 引言

機器人可以輔助或者代替人類完成重復性強、危險性高的活動，但是移動機器人的工作環境一般較為復雜，對機器人行走路線的最優化和安全性提出了較高要求。行走路徑的優劣決定了機器人的行駛安全性和工作效率的高低[1]，因此研究機器人路徑規劃問題具有重要意義。

路徑規劃是指在含有不同障礙物的環境中，按照一定的評價準則（長度最短、安全性最高、平滑性最好等），規劃出一條從起點到終點的最優無碰路徑[2]。機器人路徑規劃可以分為環境建模和路徑搜索兩個方面的內容。環境建模是指將機器人實際的工作場景抽樣為機器人可以識別的數學模型，常見方法包括柵格法、連通圖法、拓撲圖法等[3]。路徑搜索可以分為傳統路徑搜索算法和仿生搜索算法兩類，其中傳統路徑搜索算法包括人工勢場法、模擬退火法、模糊邏輯法等，仿生搜索算法包括蟻群算法、遺傳算法、粒子群算法等。人工勢場法根據障礙物斥力和目標引力規劃出路徑，路徑的平滑性較好，但是當障礙物較多時容易出現“死點”[4]。模擬退火法可以解決大規模組合優化問題，但是卻需要較長的退火時間，使算法收斂速度慢。模糊邏輯針對駕駛員的駕駛行為形成專家系統，根據路徑查表獲得駕駛路徑，此方法在環境突變時可能失效，因此靈活性較差[5]。仿生搜索算法是對生物優化的某個過程進行模擬，實現算法的智能化，是當前機器人路徑規劃的研究熱點，。文獻[6]使用人工勢場法對蟻群算法的啟發信息進行改進，此方法提高了算法的收斂速度，并減小了路徑的轉彎次數。文獻[7]在遺傳算法中引入新的遺傳因子，提出了協同進化遺傳算法，該方法加快了算法的收斂速度，并改善了解的質量。文獻[8]可以根據地圖的不同情況自適應地調節蟻群算法參數，在保證解的質量同時提高了優化效率。仿生搜索算法存在的共性問題是算法優化能力的深化，當前關于仿生搜索算法的研究均集中在這一問題上。

針對機器人在柵格環境下的路徑規劃問題，提出了復合啟發信息蟻群算法的路徑規劃策略。該方法以蟻群算法為基礎，融入了兩種啟發信息，給出了基于改進蟻群算法的規劃策略，實現了減小路徑長度、提高規劃效率的目的。

2 問題描述與建模

2.1 問題描述

這里研究的問題為柵格環境下機器人的路徑規劃問題，包括3個方面的內容：（1）柵格環境模型的建立；（2）規劃目標的設定；（3）規劃算法，其中規劃算法是核心內容。柵格模型的建立是指使用一定尺寸的方形柵格對工作環境進行分割，機器人行駛時以柵格為基本單元。柵格尺寸的設定需參考機器人直徑、環境中障礙物尺寸及復雜程度，一般來講，機器人尺寸較大、障礙物尺寸較大、障礙物分布較簡單時，柵格尺寸設置值較大。

為了保證行駛路徑的絕對安全，對障礙物一般使用膨化處理方法，即當某柵格中存在障礙物時，則讓障礙物充滿該柵格[9]，如圖1所示。

圖1 障礙物膨化Fig.1 Obstacles Expansion

另外，機器人對實際的工作環境是無法識別的，為了將實際工作環境轉化為機器人可以識別的模式，根據柵格特性為其賦不同的屬性值，當柵格中存在障礙物時為其賦值為1，當柵格中不存在障礙物時為其賦值為0。按照以上規則，圖1的工作環境可以轉化為0-1矩陣，為：

對于屬性為0的可自由行駛柵格，為了對走過的自由柵格和未走過的自由柵格進行區分，將走過的自由柵格賦值為-1，未走過的自由柵格屬性不變。則機器人可明確區分障礙物柵格、已走過的自由柵格和未走過的自由柵格。

在柵格環境下，路徑規劃的目標為機器人從起始柵格到達目標柵格的路徑最短，即目標函數為：

式中：LSG—起始柵格S與目標柵格G之間的路徑長度。

2.2 傳統蟻群算法與分析

傳統蟻群算法中，螞蟻對柵格的選擇包括8方向搜索和4方向搜索兩種，因8方向搜索的路徑平滑性更好、搜索效率更高，這里使用8方向搜索法。螞蟻對柵格的選擇是在啟發信息和信息素的雙重引導下實現的。啟發信息由目標柵格對螞蟻的啟發作用而設定，信息素是模擬蟻群協作時的交流介質而給出的。螞蟻對鄰域內自由柵格的選擇概率為[10]：

式中：i—螞蟻所在的當前柵格；j—鄰域內的待選自由柵格；k—螞蟻編號；t—迭代次數—螞蟻k由柵格i選擇柵格j的概率；τij(t)—螞蟻擇柵格j的啟發信息，τij(t)=，LjG—柵格j與目標柵格G的距離；α—啟發因子；ηij(t)—路徑ij間的信息素濃度；β—信息素因子；allowedi—柵格i鄰域的自由柵格。

在傳統蟻群算法中規定，每完成一次算法迭代，則進行一次信息素更新。信息素更新包括信息素揮發和信息素殘留兩個方面，即：

式中：ρ—揮發系數；Δτij(t)—螞蟻在路徑ij上殘留的信息素；M—螞蟻數量—螞蟻k在路徑ij上殘留的信息素；Lk—螞蟻k的路徑長度。

蟻群算法存在路徑多樣性與路徑收斂的矛盾，當路徑多樣性較好時，說明螞蟻搜索的范圍較大，但同時也說明螞蟻搜索的隨機性較大，路徑的收斂性較差。當路徑收斂性較好時，說明螞蟻搜索的方向性較好，但是同時說明螞蟻容易陷入某一局部最優路徑，螞蟻的探索能力較差。上述問題是傳統蟻群算法存在的共識問題。

3 復合啟發信息蟻群算法

3.1 復合啟發信息

為了平衡蟻群算法的路徑多樣性與收斂性，基于目標柵格的引導作用提出了兩種啟發信息。在傳統蟻群算法中，一般將待選柵格j與目標柵格G的距離倒數作為啟發信息，也就是說將待選柵格與目標柵格的遠近作為一種啟發。但是，直觀地講，螞蟻由當前柵格沿直線到達目標柵格是最佳路徑，因此將目標柵格與當前柵格的連線方向作為啟發信息，其啟發性必然強于距離信息的啟發性。按照這一思路，使用待選柵格j與目標柵格G間的向量夾角θ構造啟發信息。夾角示意圖，如圖2所示。

圖2 待選柵格向量與目標柵格向量夾角Fig.2 Angle Between Selected Grid Vector and Target Grid Vector

在圖2 中，當前柵格坐標記為(xi，yi)，待選柵格坐標記為(xj，yj)，目標柵格坐標記為(xG，yG)。由直觀理解可知，螞蟻搜索的最佳方向為D→iG=(xG-xi，yG-yi)，實際搜索方 向為D→ij=(xj-xi，yj-yi)，在此將兩個向量的夾角定義為兩者之間的真角，因此取值范圍為θ∈[0，π]。以夾角θ為基礎，構造兩種啟發信息。啟發信息1為：

啟發信息2為：

對于啟發信息1 和啟發信息2，當θ∈[0，π]范圍內，ηij1和ηij2均為單調遞減函數，這意味著夾角θ越小（此時待選柵格越靠近最優方向），對應柵格對螞蟻的啟發能力越強，螞蟻更容易選擇這一柵格；夾角θ越大（此時待選柵格越遠離最優方向），對應柵格對螞蟻的啟發能力越弱，螞蟻越不容易選擇這一柵格。以上分析表明，2種啟發信息的構造方法是合理的。啟發信息1和啟發信息2的ηij值隨夾角θ的變化趨勢，如圖3所示。

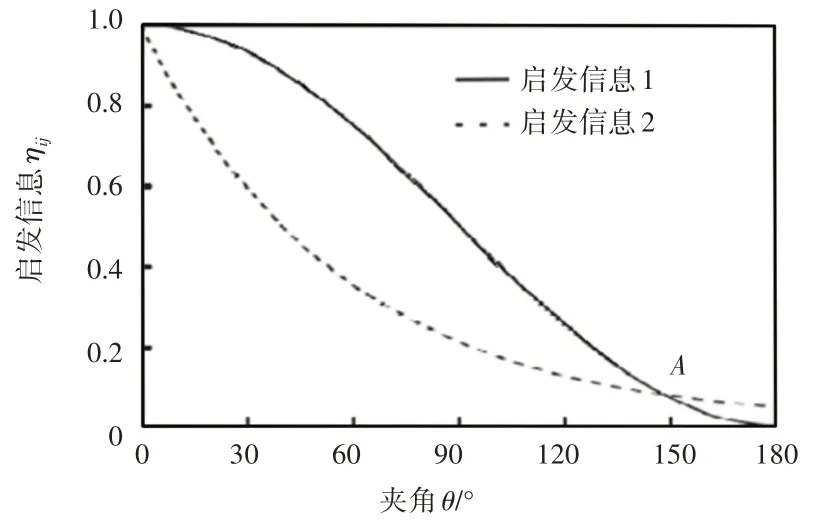
圖3 啟發信息變化趨勢Fig.3 Changing Tendency of Inspiration Information

經計算圖3中的交點A橫坐標為148.1°，這意味著幾乎在整個θ的取值范圍內，當ηij值相同時，相應的有θ1>θ2。也就是說，在相同啟發信息范圍的情況下，夾角θ1的變化范圍大于夾角θ1的變化范圍，說明啟發信息1可以指導螞蟻進行更大角度范圍的搜索，而啟發信息2的方向性較強，可以指導螞蟻沿著最佳方向進行搜索。為了對上述分析進行更加直觀的解釋，設置ηij1=ηij2>0.5，則夾角θ1∈(0，90°)，θ2∈(0，39.7°)，如圖4所示。由圖4可直觀看出，啟發信息1的搜索范圍更廣，而啟發信息2的搜索方向性更強。

圖4 啟發信息1和啟發信息2對比Fig.4 Comparison of Inspiration Information 1 and Inspiration Information 2

3.2 復合啟發信息蟻群算法

根據蟻群算法的路徑規劃需求，算法前期需要較大的搜索范圍，以便對工作區域的最優路徑進行廣泛搜索；算法后期需要較強的方向性搜索，以便算法收斂于最優路徑附近，并進行最優路徑附近的細致搜索。按照算法上述的需求分析，提出的改進蟻群算法思想為：前期設置較大數量的啟發信息1螞蟻，以便進行大范圍搜索；后期設置較大數量的啟發信息2螞蟻，以便進行方向性強的小范圍細致搜索。

根據算法的需求分析，算法前期蟻群中設置更多的啟發信息1類的螞蟻，隨著算法的迭代，啟發信息1類的螞蟻數量逐漸減少，而增加啟發信息2類的螞蟻。這種設置方法兼顧了前期大范圍搜索需求和后期方向性較強的搜索需求。蟻群規模記為N，算法的最大迭代次數記為tmax，啟發信息1類的螞蟻數量記為N1，啟發信息2類的螞蟻數量記為N2，則兩類螞蟻的數量設置為：

式中：t—當前迭代次數。

分析式（6）可知，隨著算法的迭代，啟發信息1類的螞蟻逐漸減少，啟發信息2類的螞蟻逐漸增多，滿足前文的構造需求。

兩類螞蟻之間的交流通過信息素實現，即通過路徑上殘留的信息素濃度可以實現螞蟻之間的交流與協作。

3.3 基于復合啟發信息蟻群算法的路徑規劃步驟

根據復合啟發信息蟻群算法的原理，結合柵格環節下機器人路徑規劃的特點，設置基于復合啟發信息蟻群算法的機器人路徑規劃步驟為：

（1）設置柵格環境規模、起點柵格、終點柵格；設置算法參數，包括螞蟻數量、信息素因子、啟發因子、信息素揮發系數、算法最大迭代次數等；（2）將螞蟻放置在起始柵格，開始路徑規劃；（3）兩類螞蟻按照各自的啟發信息進行柵格選擇，得到各自規劃出的路徑；（4）判斷是否所有螞蟻完成了一次迭代，若否則等待；若是則迭代i次數＋1；（5）判斷是否達到最大迭代次數，若否則轉至（2）；若是則輸出最優路徑，算法結束。

4 仿真驗證

4.1 啟發信息效果驗證

首先在（30×30）規模的柵格環境下驗證路徑規劃效果，工作環境中障礙物柵格的比例設置為10%和20%兩種情況，起始柵格設定為左上角柵格，目標柵格設置為右下角柵格。算法的參數設置為：螞蟻規模為50，信息素因子為1.5，啟發因子為4.0，信息素揮發系數為0.4，算法的最大迭代次數為100，計算環境為Win?dowsl0、i5CPU、內存8GB，仿真軟件為Matlab2017。

在障礙物柵格占比為10%和20%兩種情況下，分別使用啟發信息1蟻群算法和啟發信息2蟻群算法進行10次路徑規劃，障礙物占比為10%的最優路徑，如圖5所示。障礙物占比為20%的最優路徑，如圖6 所示。在一些實驗中得到的最優路徑是重合的，因此圖中給出的最優路徑數量小于10。

圖5 障礙物占比10%的規劃結果Fig.5 Planning Result of 10% Barrier Environment

圖6 障礙物占比20%的規劃結果Fig.6 Planning Result of 20% Barrier Environment

對比圖5和圖6中兩種啟發信息蟻群算法的規劃結果可以看出，10次規劃得到的路徑中，啟發信息1蟻群算法規劃的路徑范圍更加廣泛，這意味著啟發信息1 蟻群算法的搜索全局性更好；而啟發信息2蟻群算法規劃的路徑范圍相對較小，這意味著啟發信息2蟻群算法搜索的路徑方向性更好。該實驗現象與3.1節的設計原理完全一致，驗證了兩種啟發信息設置的合理性。

4.2 與傳統蟻群算法比較

為了進一步驗證復合啟發信息蟻群算法在柵格環境中路徑規劃的可行性，設置（30×30）規模的柵格工作環境，分別使用復合啟發信息蟻群算法和傳統蟻群算法進行10次路徑規劃，統計10次最優路徑的最短距離、標準差、迭代次數，如表1所示。復合啟發信息蟻群算法和傳統蟻群算法搜索的最短路徑，如圖7所示。

表1 傳統蟻群與復合啟發蟻群對比Tab.1 Comparison of Compound Inspiration Ant Colony and Traditional Ant Colony

圖7 復合啟發蟻群與傳統蟻群規劃結果Fig.7 Planning Result of Compound Inspiration Ant Colony and Traditional Ant Colony

結合表1和圖7可以看出，10次規劃的最優路徑中，傳統蟻群算法規劃的最優路徑長度為68.021，路徑的標準差為4.251，復合啟發信息蟻群算法規劃的最優路徑長度為52.545，路徑標準差為2.211，這說明復合啟發信息蟻群算法規劃的最優路徑比傳統蟻群算法規劃結果更優，且路徑規劃的穩定性更強，這是因為復合啟發信息蟻群算法中引入了兩種啟發信息，啟發信息1搜索的全局性好，而啟發信息2搜索的方向性好，這樣兼顧了算法的優化能力和穩定性，因此復合啟發信息蟻群算法的規劃結果優于傳統蟻群算法。

4.3 與其余改進蟻群算法比較

為了進一步對比規劃策略與其余規劃策略的路徑優劣，選擇文獻[11]的改進蟻群算法進行比較。在（30×30）規模的柵格環境中，分別使用復合啟發信息蟻群算法和文獻[11]蟻群算法進行10次路徑規劃，得到的最短路徑，如圖8所示。

圖8 復合啟發蟻群與文獻蟻群規劃結果Fig.8 Planning Result of Compound Inspiration Ant Colony and Ant Colony in Essay

經統計，復合啟發蟻群算法規劃的最短路徑長度為43.355，規劃出最優路徑的迭代次數為41；文獻[11]參數優化蟻群算法規劃的最短路徑長度為46.113，規劃出最短路徑的迭代次數為57。以上數據表明，復合啟發信息蟻群算法規劃的路徑更短，且規劃效率更高。這是因為文獻[11]只是使用粒子群算法對蟻群算法的參數進行了優化，并未從原理上解決多樣性和收斂性之間的矛盾。而這里提出的復合啟發信息蟻群算法在算法中引入了兩種啟發信息，一個啟發信息具有更大的搜索范圍，另一個啟發信息具有更好的搜索方向性，因此兼顧了算法的多樣性和收斂性，從根本上改善了算法性能。綜合以上分析，本文提出的復合啟發信息蟻群算法在柵格環境路徑規劃中是有效的，可以得到更短路徑，且規劃效率較高。

5 結論

研究了機器人在柵格環境下的路徑規劃方法，提出了兩種啟發信息，將兩種啟發信息融入到蟻群算法中，得到了兼顧多樣性和收斂性的蟻群算法。將復合啟發信息蟻群算法應用于路徑規劃中，得到以下結論：

（1）提出的兩種啟發信息中，啟發信息1具有較大的搜索范圍，啟發信息2具有更強的搜索方向性；

（2）復合啟發信息蟻群算法規劃的路徑優于傳統蟻群算法，且規劃效率更高。