一種彈道修正彈SINS任意滾轉角快速粗對準方法

王晗瑜,申 強,胡寶遠,鄧子龍,李 巖

(1. 北京理工大學機電學院,北京 100081；2. 北京理工大學重慶創新中心,重慶 401120；3. 西北工業集團有限公司設計二所,西安 710043)

0 引 言

二維彈道修正彈藥是一類介于無控炮彈與制導炮彈之間的新型信息化彈藥,通過彈載導航及彈道參數測量、簡易修正模塊提高打擊精度,減少附帶毀傷。其中,彈體姿態信息用于加速度計測量信號坐標轉換、彈體姿態控制等,姿態估計精度直接影響彈道修正精度。

地磁傳感器是目前國際上低成本修正彈藥最主要的姿態測量手段,但精度偏低,測姿誤差最大可達10°,無法滿足彈體姿態控制要求,且極易受到強磁環境干擾,彈體飛行方向平行于地磁場方向時,存在奇異值。隨著微機電慣性傳感器成本降低、體積縮小、抗過載能力加強,其在智能彈藥上的應用逐漸成為可能。基于多加速度計的無陀螺慣性測量方法標定及計算過程復雜,精度受安裝結構影響較大,且無法滿足彈道修正彈藥成本低、傳感器數量少的要求,工程實現可行性較低。結合彈體飛行動力學的微慣性姿態測量方法依賴于對系統模型和初始姿態的準確描述,計算成本高且不適用于滾轉姿態完全未知的炮射彈藥。基于衛星/微慣性傳感器的組合測姿方法可實現低成本滾轉姿態解算,但是衛星信號易受到電磁干擾,戰時強對抗條件下可用性嚴重降低。無線電信標技術已用于一些武器的陸基導航,發展無線電信標/微慣性組合導航系統對于提高彈道修正彈藥戰場生存能力具有重要意義。Wright等驗證了基于無線電信標測量位置速度的可行性,指出當彈體位于信標上方、信標布設分散且有幾十米高程差情況下,可以達到與衛星導航系統同等的測量精度。然而實際戰場環境中,對于射程一般在十幾到幾十公里的炮射彈藥,信標僅可在炮位區域布設,布設個數、范圍及地形有限,往往無法提供長時間、高精度、完整的三維測量信息,估計彈體姿態時可觀性較差。

初始對準是慣性導航精確解算的前提,炮射彈藥發射后彈丸滾轉角處于隨機狀態。為解決捷聯慣導大失準角空中初始化這一問題,孟東等、梅春波等建立了非線性卡爾曼濾波模型,Wang等、梅春波等建立了基于四元數的卡爾曼濾波模型。這些方法計算復雜,收斂速度慢,初始失準角過大時模型失效,無法滿足炮射彈道修正彈藥需要；同時,微慣導噪聲源復雜,零偏特性受到高過載沖擊后會發生改變,難以精確建模。神經網絡具有很強的非線性函數逼近能力和容錯能力,因此一些學者提出用神經網絡模型替代卡爾曼濾波的初始對準方法,Rafatnia等建立了遞歸小波神經網絡模型,實現了微慣性傳感器非高斯白噪聲和不確定偏差情況下的動基座對準,顯著提高了對準精度。但是該方法需要在運動過程中實時訓練,不適用于計算能力有限、飛行時間較短的彈道修正彈藥。

考慮到彈道修正彈藥發射后彈道特征已知,本文提出了利用彈道模型線下預訓練神經網絡,擬合初始滾轉角與觀測信息間非線性映射關系的方法,提高粗對準速度與精度。由于炮口處少量信標測量信息與姿態耦合關系較弱,失準角為弱可觀狀態,本文顯性提取了捷聯慣導自身測量參數作為輸入神經元,提高了網絡預測精度。

本文的結構安排為：首先建立初始滾轉角與捷聯慣導、無線電信標測量參數的函數模型,為建立神經網絡模型奠定理論基礎；然后采用主成分分析法優化網絡模型,結合彈體飛行過程生成訓練、測試數據；最后通過仿真模擬驗證函數模型及提出的網絡模型在對準速度、精度和適用失準角范圍等方面的優越性,且具有很好的魯棒性。

1 初始滾轉角非線性函數模型

本文定義的相關坐標系如圖1所示。

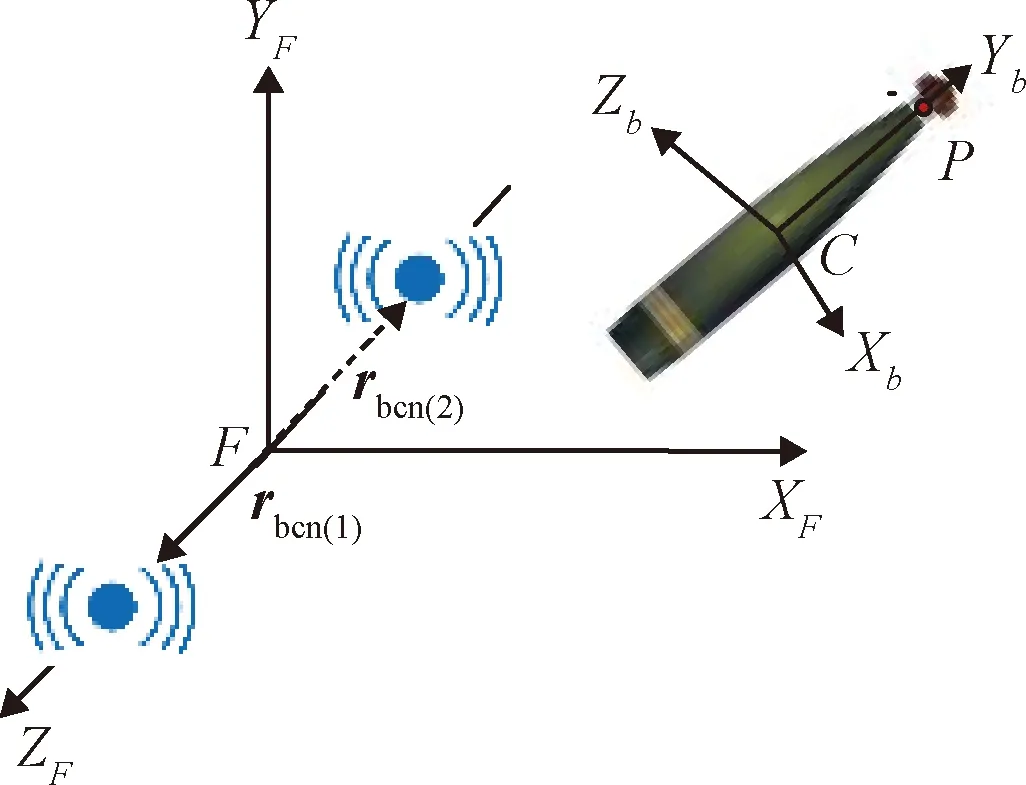
圖1 彈體坐標系與發射坐標系Fig.1 Body coordinate system and launching coordinate system

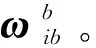
(2)發射坐標系。原點是發射點在大地水準面上的投影,軸為彈道面和水平面的交線,射向為正,軸鉛直向上,軸與軸、軸構成右手直角坐標系指向鉛直面右方。為簡化計算,本文取射擊方位角為0°。考慮到彈道修正彈藥射程近(小于50 km),飛行時間短,且微機電陀螺儀精度較低,因此將發射坐標系作為導航參考坐標系系,并忽略地球自轉帶來的影響。

考慮實際戰場環境對無線電信標布設的簡便性及快速性要求,在炮口左右兩側m各布設一信標。信標在發射坐標系下坐標分別為=(0,0,),=(0,0,-)。

1.1 初始滾轉角與捷聯慣導測量參數函數模型

根據捷聯慣導反演算法,發射坐標系下的比力經過坐標轉換后可以得到彈體坐標系下比力。

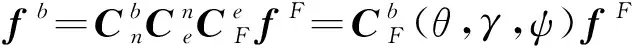
(1)

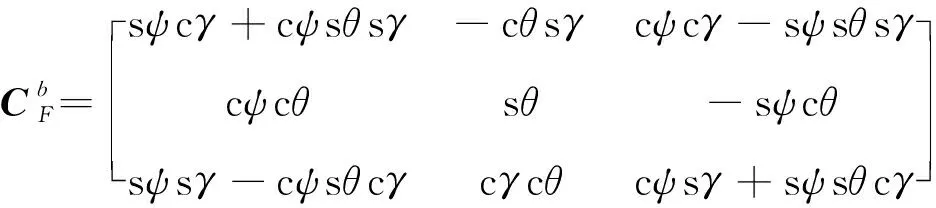
(2)

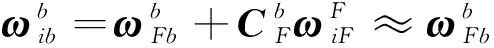
(3)

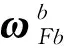
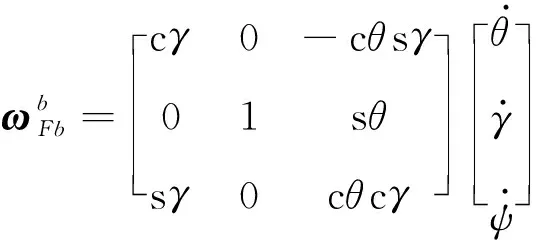
(4)

式(3)～(4)表示了陀螺儀測量角速度與滾轉角之間的非線性函數模型,且僅軸、軸角速度與滾轉角存在映射關系。

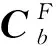
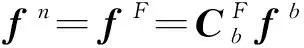
(5)

由式(1)可知是滾轉角的函數,因此可得到導航系下比力與滾轉角之間的函數模型。

1.2 初始滾轉角與無線電信標測量信息函數模型

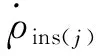
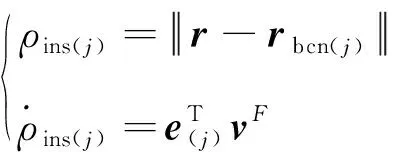
(6)

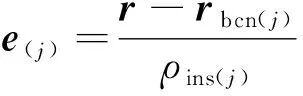
(7)

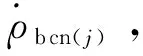
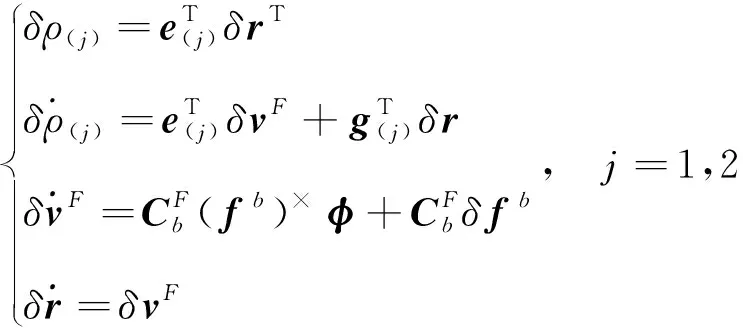
(8)

(9)

式中：δ為捷聯慣導解算速度誤差,δ為捷聯慣導解算位置誤差,()為的反對稱陣,定義見文獻[13]。

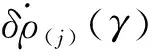
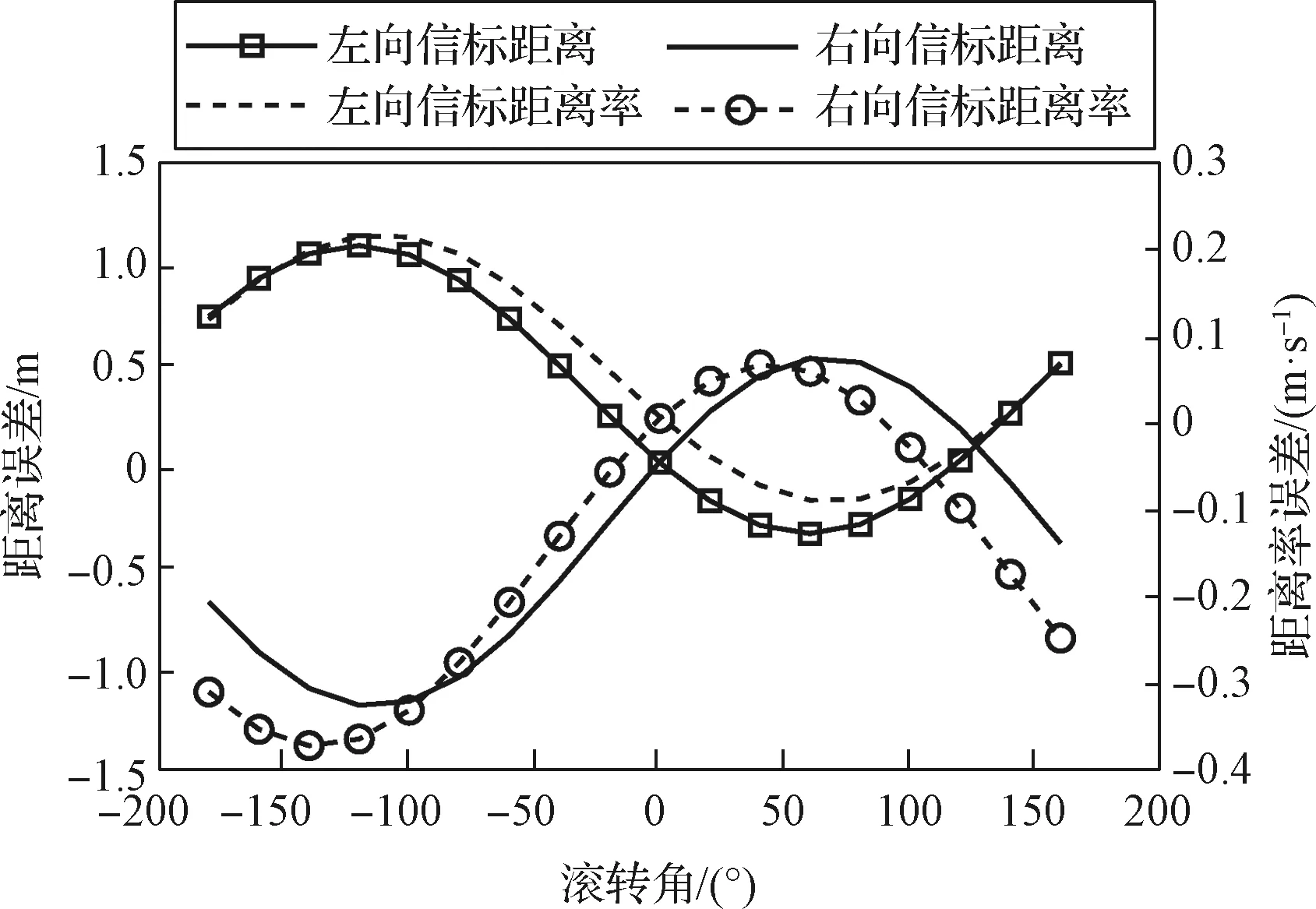
圖2 5 s內捷聯慣導解算積累的距離、距離率誤差Fig.2 Accumulated range and rate errors of SINS within 5 s

卡爾曼濾波模型的狀態量包括彈體在發射坐標系下的3維位置、速度和轉速。即：

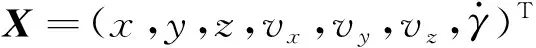
(10)

狀態方程為剛體4D彈道方程,狀態方程及狀態轉移矩陣()見文獻[14]中相關結論。

觀測量為信標接收機輸出的距離和距離率：

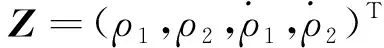
(11)

觀測方程為

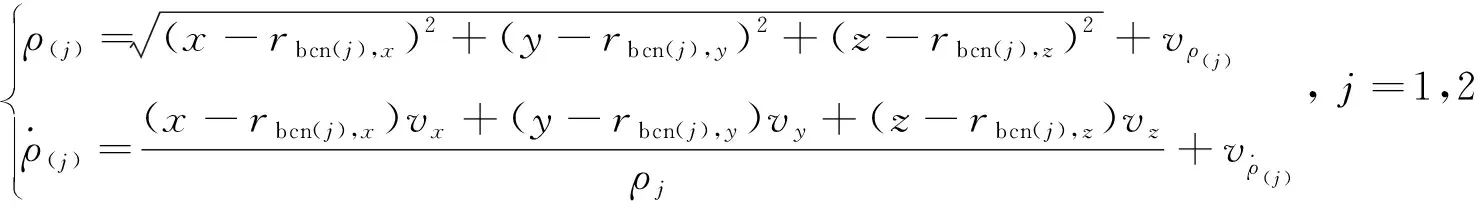
(12)

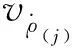
(13)

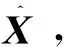
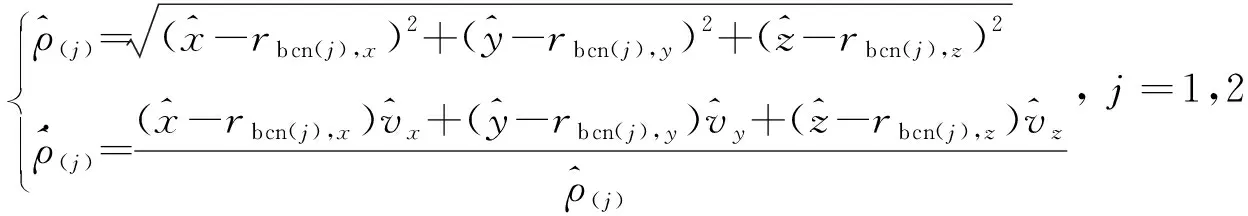
(14)

2 基于BP神經網絡的彈道修正彈藥粗對準模型

在第1節中建立了與初始滾轉角有關的函數模型,傳統對準方法在上述函數基礎上建立非線性卡爾曼濾波模型,收斂速度慢,失準角較大時模型失效,不適用于炮射彈道修正彈藥。根據Kolmogorov定理,三層神經網絡在隱含層節點個數足夠的情況下,就可對非線性函數進行無限逼近。因此,可利用神經網絡這一特性逼近式(1)～(5)、式(8),對彈體滾轉角進行快速估計。

2.1 BP神經網絡輸入輸出參數選取策略

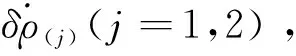
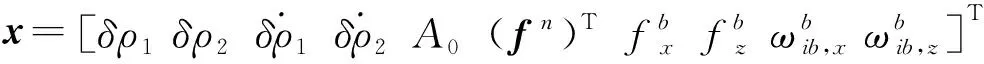
(15)

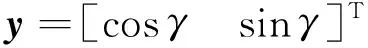
(16)

2.2 BP神經網絡特征提取

式(15)選擇的輸入特征之間具有較強的相關性,導致網絡模型結構復雜,訓練時容易陷入局部最小值點,模型泛化能力變差。因此,本文采用了主成分分析(Principal components analysis,PCA)的方法進行特征提取,將原始輸入變量線性變換為一組不相關的主成分,同時盡可能保留原始變量中的主要信息。該算法詳細步驟如下：

對于維輸入變量,每維變量有個樣本,即：

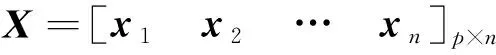
(17)

1) 數據標準化。

2) 計算相關系數矩陣。

3) 計算相關系數矩陣的特征值(=1,2,…,)及相應的特征向量,并按照特征值降序排列。

4) 根據式(18)～(19)計算各特征值的貢獻率(=1,2,…,)和累積貢獻率(=1,2,…,),選擇累積貢獻率達到95%以上的特征值作為主成分。

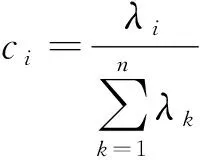
(18)

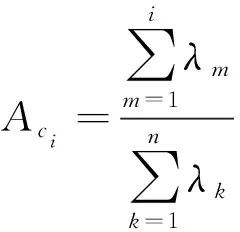
(19)

2.3 BP神經網絡訓練、測試數據模擬

生成測試數據時,不僅考慮了實測慣性傳感器靜態噪聲及信標接收機模擬噪聲,并且為驗證模型泛化能力,設置了射角、俯仰角對準誤差不在訓練范圍內以及信標位置存在誤差的測試環境,參數設置見表1。其中,射角間隔在測試環境A中設置為1°,其他測試環境中設置為2°,俯仰角對準誤差間隔均為1°。

表1 測試數據參數設置Table 1 Test data parameters set

3 仿真校驗及模型評估

3.1 神經網絡非線性函數模型驗證

初始滾轉角與慣導自身參數函數關系驗證

以某型榴彈彈體飛行軌跡為例,射角35°,初始合速度930 m/s時,飛行總時間為96 s,總射程為29.34 km。令=5 s,=10 s,圖3驗證了由式(1)～(9)表示的非線性函數(以軸為例),并引入了傳感器實測噪聲。其中加速度計零偏均值分別為1.15×10,2.8×10,9.2×10,陀螺儀零偏均值分別為27.86(°)/h,49.97(°)/h和2.58(°)/h。

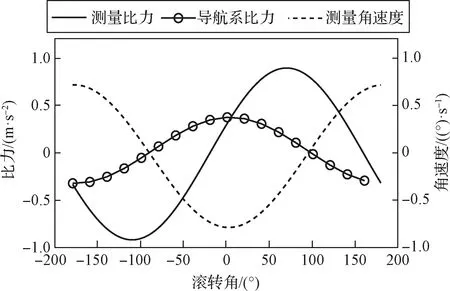
圖3 初始滾轉角與x軸比力、角速度關系Fig.3 Relations between the initial roll angle and x-axis specific force and angle rate

初始滾轉角與測距測速誤差函數關系驗證

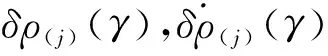
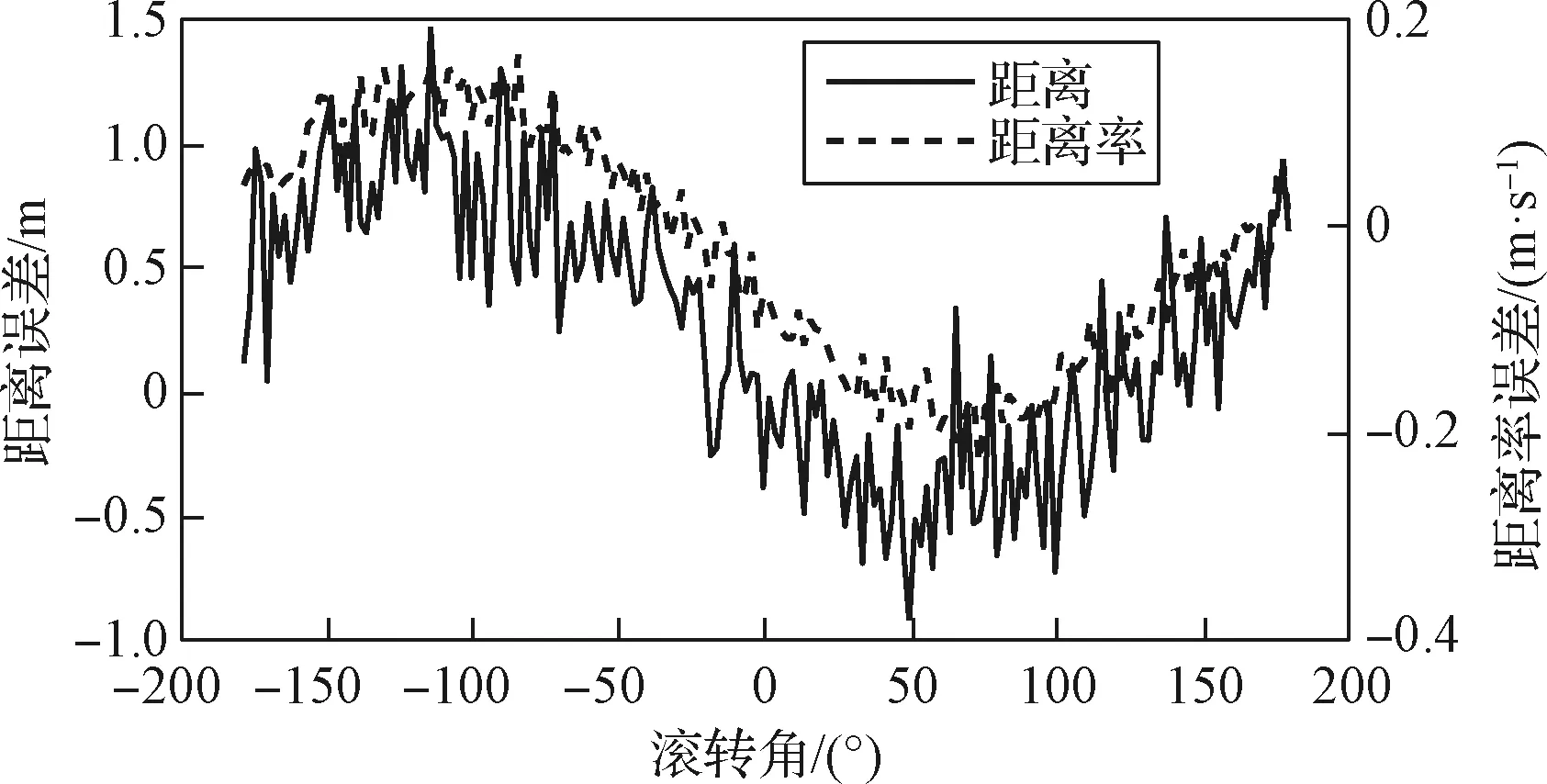
圖4 濾波后左側信標測量距離、距離率精度隨滾轉角變化Fig.4 Curves of the filtered range error and range rate error measured by the left beacon with the roll angle

3.2 基于神經網絡的粗對準模型評估

神經網絡采用單隱藏層結構,隱藏層神經元個數為5,由帶動量因子的和具有自適應學習速率梯度下降的traingdx函數訓練,最大訓練輪數設置為5000。根據式(18)～(19),前6維主成分累計可信度可達99.89%。因此,本文建立的PCA-BP神經網絡輸入神經元為6維。

用于模型評價的精密度指標為預測結果的均方根誤差(RMSE),準確度指標包括平均絕對誤差(MAE)與最大絕對誤差(Max-AE)。

多輸入神經網絡模型精度評估

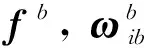
表2 模型一、二預測結果Table 2 Prediction results of Model 1 and Model 2

可以看出,在測試環境A下,模型一的預測精密度及準確度遠遠優于模型二。這說明,僅依賴于炮口信標提供的距離、距離率信息的模型可觀測度很差,增加捷聯慣導測量信息作為輸入層神經元可以顯著提高網絡的預測精度。

模型快速性及適用失準角范圍評估

炮射彈道修正彈飛行時間較短,且發射后滾轉角處于隨機狀態,模型必須實現任意初始狀態下快速對準。本模型中,無線電信標測速精度是制約粗對準時間的主要影響因素,即只有當濾波之后的測量噪聲小于(-)時間內積累的距離率誤差時,該對準模型才是有效的。

為有效評估本模型的快速性,分別模擬了無線電信標測速誤差為0.1 m/s,0.5 m/s和1 m/s時所需的對準時間。經過卡爾曼濾波之后,無線電信標測速誤差分別為0.034 m/s,0.163 m/s和0.341 m/s。不同對準時間下,距離率誤差隨滾轉角變化的平均絕對值見表3,因此,當無線電信標測速誤差為0.1 m/s時,需滿足對準時間≥10 s；測速誤差為0.5 m/s時,需滿足≥17 s；測速誤差為1 m/s時,需滿足≥20 s。

表3 不同時刻下平均絕對距離率誤差Table 3 Average absolute range rate errors at different times

以射角35°為例,在A組測試環境下,模擬了不同測速精度的信標輔助下,對準精度隨對準時間變化,見表4。可以看出,對準時間越長,對準精度越高,但受到網絡模型限制,超過一定時間,對準精度提高不再明顯,因此實際應用時,取網絡模型最短對準時間進行粗對準,再切換到精對準,可提高對準效率。

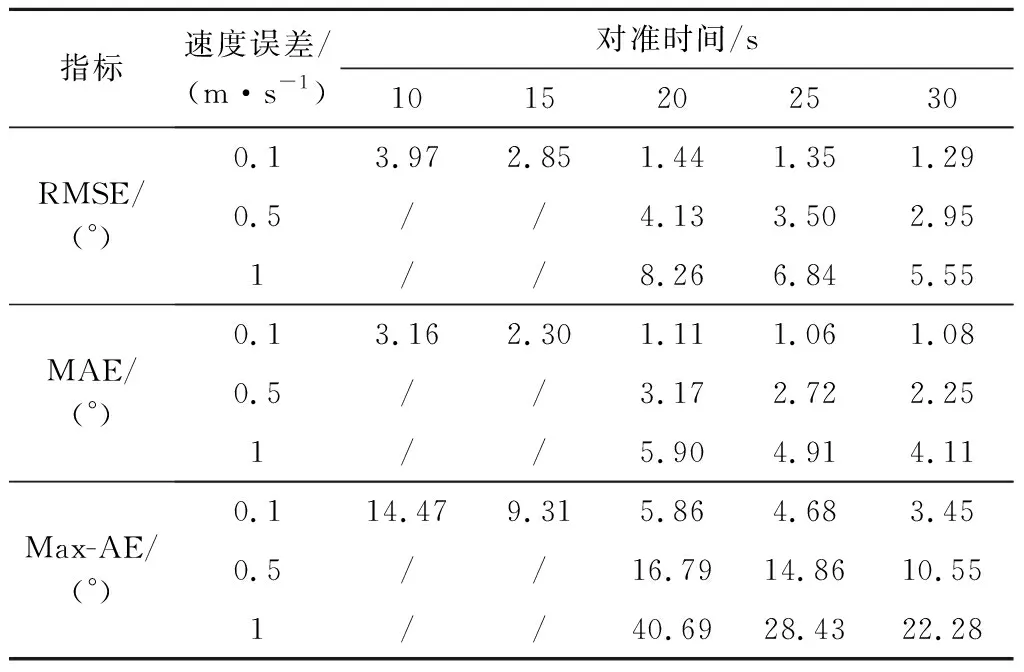
表4 對準結果與信標測速誤差、對準時間的關系Table 4 Relations between the alignment results and the beacon-measured range rate errors and alignment time

少量信標輔助下,線性卡爾曼濾波可快速收斂的最大初始誤差范圍在20°～30°,因此假定30 s內滾轉角誤差可收斂到25°內時,該粗對準模型有效。為進一步驗證本文提出的粗對準模型快速性及失準角適用范圍廣泛性,以射角35°為例,在A組測試環境下,對比了基于擴展卡爾曼濾波(Extended Kalman filter, EKF)的非線性卡爾曼對準模型和基于加性四元數誤差(Additive quaternion error, AQE)的線性卡爾曼對準模型,可有效收斂的初始失準角范圍和該范圍內最大失準角下完成粗對準所需時間見表5。不同初始誤差下的對準結果如圖5所示,其中PCA-BPNN模型以信標測速誤差為1 m/s為例。可以看出,本文提出的基于神經網絡的粗對準模型可在任意失準角范圍內快速完成粗對準,其適用角度廣泛性和快速性明顯優于傳統的卡爾曼濾波方法。

表5 不同模型適用失準角范圍和對準時間對比Table 5 Comparison of applicable misalignment angle ranges and alignment time of different models

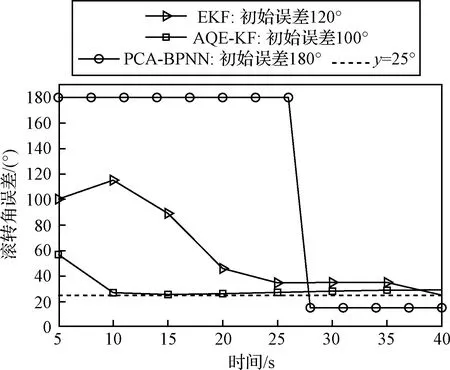
圖5 不同模型粗對準結果對比Fig.5 Comparison of the coarse alignment results of different models

模型魯棒性評估

為評估本文提出的粗對準模型在實際作戰使用時的魯棒性,以信標測速誤差0.1 m/s為例,在射角未在訓練范圍內的場景B、射角與初始俯仰角誤差均不在訓練范圍內的場景C及考慮信標布設位置誤差的場景D下進行測試,并與未進行優化的BPNN進行對比,結果見表6。其中同一測試環境下精度較高的結果用粗體表示。

從表6可以看出,三種測試場景下,PCA-BPNN的均方根誤差和平均絕對誤差在8°以內,最大絕對誤差在25°以內,且能在發射后10 s前完成,滿足彈道修正彈粗對準精度要求。

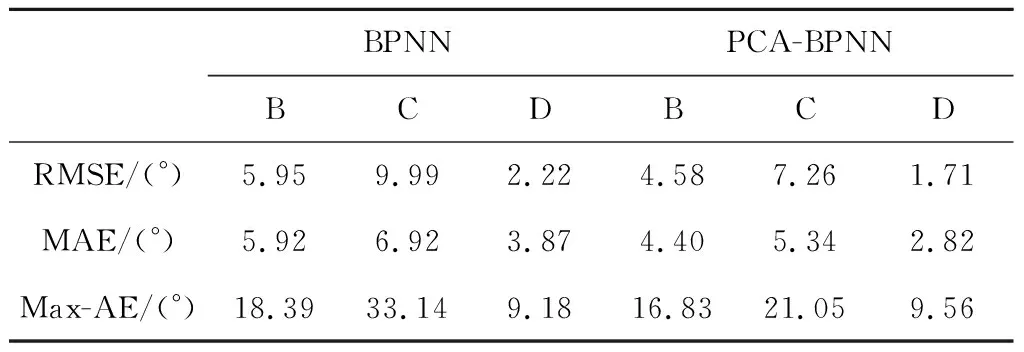
表6 不同測試環境下BPNN和PCA-BPNN預測結果Table 6 Prediction results of BPNN and PCA-BPNN in various testing environments

同信標布設位置誤差相比,未在訓練范圍內的射角和初始俯仰角誤差對最大絕對誤差值影響較大。因此使用時盡量對所有可能的射角范圍和初始俯仰角誤差范圍進行訓練,以獲得更高的對準精度；本方法對信標布設精度沒有很高的要求,實際應用具有較高的簡便性。

同BPNN相比,本文提出的PCA-BPNN模型在B, C, D多種測試環境下預測精密度和準確度均明顯優于BPNN。建立的PCA-BPNN不僅由較少的輸入變量組成,具有簡單的網絡結構,在彈載計算機上離線應用時計算量小；并且由于輸入數據降維有利于神經網絡參數的優化迭代,提高了網絡模型的預測精度和泛化能力。

綜上所述,與基于非線性卡爾曼濾波進行大失準角粗對準的經典方法不同,本文提出的方法結合彈道模型線下訓練BP神經網絡,在應用時僅需將訓練好的網絡保存到彈載計算機中,計算簡單,便于實現,對準速度快,在-180°～180°的失準角范圍內都具有較高精度。

4 結 論

針對炮射彈藥發射后滾轉角完全未知且信標測量值可觀性較差的難點,本文提出了結合彈道模型建立優化后的神經網絡模型進行線下訓練,并加入捷聯慣導參數作為輸入神經元的快速粗對準方法。仿真結果表明,無論失準角大小,本文提出的粗對準方法均可在發射后10 s內快速完成對準,相比于傳統基于卡爾曼濾波的對準方法,快速性、對準范圍及魯棒性均明顯提高,為炮射彈道修正彈藥出炮口后任意滾轉角條件下的快速粗對準提供了參考。