天問一號環繞器中繼軌道受攝共振特性分析

朱新波,李海洋,鄭惠欣,徐 亮

(1. 南京航空航天大學航天學院,南京 211106；2. 上海衛星工程研究所,上海 201109；3. 上海市深空探測技術重點實驗室,上海 201109)

0 引 言

“天問一號”火星探測器于2021年2月10日成功完成火星制動捕獲,成為我國首個環繞火星的探測器。2021年5月15日,“祝融”火星車成功著陸火星北半球的烏托邦平原。火星探測一直是深空探測的熱點,而且其中也有著諸多學術問題亟待研究。火星大氣進入問題始終是學術界的研究熱點,也有一系列與天問一號大氣進入相關的高水平研究與應用成果發表。除了火星大氣進入問題,環火受攝軌道動力學研究同樣對火星探測具有重要意義。

在火星車火星表面工作期間,位于環火軌道的“天問一號”環繞器為火星車與地面站提供中繼服務。環繞器在中繼任務期間必須運行在合適的中繼軌道上,才能夠提供穩定可靠的中繼服務。但由于環繞器在環火軌道上受到火星非球形攝動、大氣攝動、第三體引力攝動等影響,中繼軌道星下點會出現漂移,無控情況下會導致中繼弧段受到影響,甚至無法滿足中繼條件。對于常見的火星環繞軌道,影響最主要的是火星非球形攝動,其中最受關注的是帶諧項。已有研究主要包括帶諧項攝動下的環火軌道特性或者軌道演化規律。而已有的火星探測任務,也主要位于低軌近圓軌道,根據探測任務需求,也主要利用帶諧項攝動設計其軌道漂移特性。

一般軌道設計中所考慮的最主要的攝動項為帶諧項,但是田諧項也會在某些情況下起到重要作用,如地球同步軌道衛星的軌道漂移現象。關于田諧項對環火軌道的影響并沒有太多研究,但是本文分析表明,火星環繞器的中繼軌道星下點漂移在帶諧項攝動模型與考慮田諧項的高精度軌道模型兩種情況下呈現出完全不同的特性,這一特性正是由田諧項產生的軌道共振導致。對于本文所考慮的環火軌道,如果仍然采取軌道設計中通用的帶諧項分析進行設計,其關鍵特性將會得到完全不同的結果,從而影響到任務實施。因此,研究清楚田諧項攝動與中繼軌道漂移特性的關系具有十分重要的意義。

本文首先對環繞器中繼軌道星下點漂移的特殊現象進行了描述,然后通過數值實驗的方法,分析了不同攝動項對中繼軌道星下點漂移特性的影響,從中找到了田諧項是導致特殊漂移特性的主要因素；接著通過對星下點過著陸點緯度時的經度進行簡化計算,將原因進一步定位到軌道半長軸增大；最后,通過對攝動項的數學分析,發現田諧項導致的軌道共振是該問題的根本原因。

1 現象描述

1.1 “天問一號”環火軌道簡述

“天問一號”環繞器的環火軌道為大偏心率、傾角接近90°的軌道,整個任務過程中主要分為三個階段。

第一階段：停泊軌道。火星車著陸前,需要在該軌道上對預定著陸區開展詳查。停泊軌道周期約為兩個火星日(49.2 h),可保證探測器每兩個火星日就可以對預定著陸區開展一次詳查。

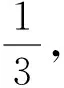
第三階段：遙感軌道。環繞器在中繼軌道工作完成后進入科學探測遙感軌道,對火星進行科學探測,兼顧為火星車提供中繼通信服務。遙感探測主要在近火點附近進行,而近火點幅角受火星非球形攝動會在火星緯度方向進行漂移,從而實現對火星全球的覆蓋。

由于中繼任務階段環繞器與火星車之間的通信是否可見受軌道漂移影響較大,對軌道攝動更為敏感,本文重點關注環繞器中繼任務階段的軌道受攝問題。

1.2 中繼軌道星下點漂移

由于軌道攝動,環繞器在中繼軌道運行時星下點并不會始終保持在著陸點上空,而是會出現漂移。分析采用的火星慣性系下的平均軌道根數如下。

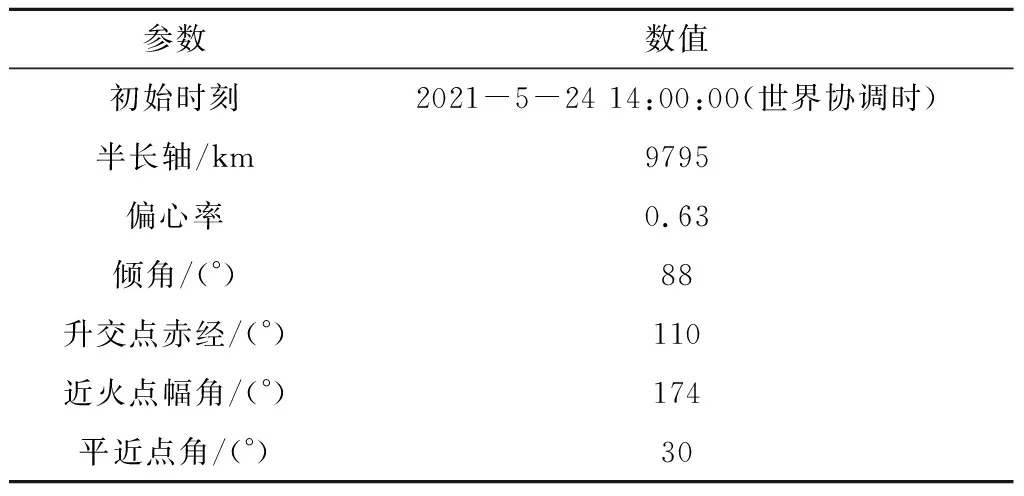
表1 火星慣性系下中繼軌道平均軌道根數Table 1 Mean orbital elements in Mars inertial frame

計算使用全攝動模型,考慮了120階的JGMRO120 d火星引力場模型、第三體引力攝動、太陽光壓攝動和大氣阻力攝動,其具體軌道遞推計算公式可參見文獻[20-21]。工程實踐表明該模型能夠非常好地表示真實軌道。

環繞器進入中繼軌道后,在不進行軌道維持的情況下,30天內星下點軌跡如圖1所示。星下點過著陸點緯度時的經度隨時間變化情況如圖2所示。星下點計算公式可參見文獻[20-21]。

圖1 環繞器星下點軌跡漂移Fig.1 The orbiter’s sub-satellite point trajectory drifts

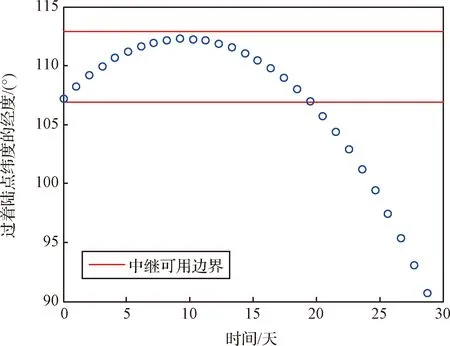
圖2 環繞器過著陸點緯度的經度隨時間變化Fig.2 Variation of the orbiter’s longitude passing the latitude of landing site over time

由于各種工程約束存在,當環繞器星下點經度漂移著陸點較遠時,就無法再提供中繼通信服務。圖2中兩條紅線之間的區域表示中繼可用的區域。從圖中可以看到,當環繞器進入中繼軌道后,前10天內星下點過著陸點緯度的經度先隨時間遞增到最大值,后20天內隨時間遞減,該變化趨勢既不是單調變化,也不是短周期性變化。

軌道設計中一般認為,對于非同步軌道,考慮中心天體的非球形攝動至4階帶諧項已經可以較高精度地反映軌道攝動變化的主要特征。考慮火星主要非球形攝動項后,平均軌道根數表示的軌道長期項變化率如下式：

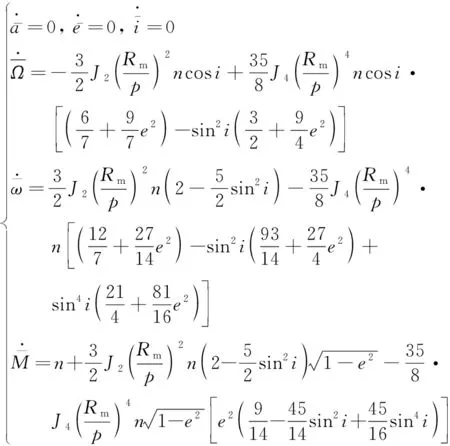
(1)

式中：表示軌道半長軸,表示軌道偏心率,表示軌道傾角,表示升交點赤經,表示近火點幅角,表示平近點角,表示軌道角速度,表示軌道半通徑,表示火星平均赤道半徑。

將中繼軌道采用火星非球形攝動項進行軌道遞推,可以得到在該模型下環繞器30天內星下點過著陸點緯度時的經度隨時間變化情況,如圖3所示。

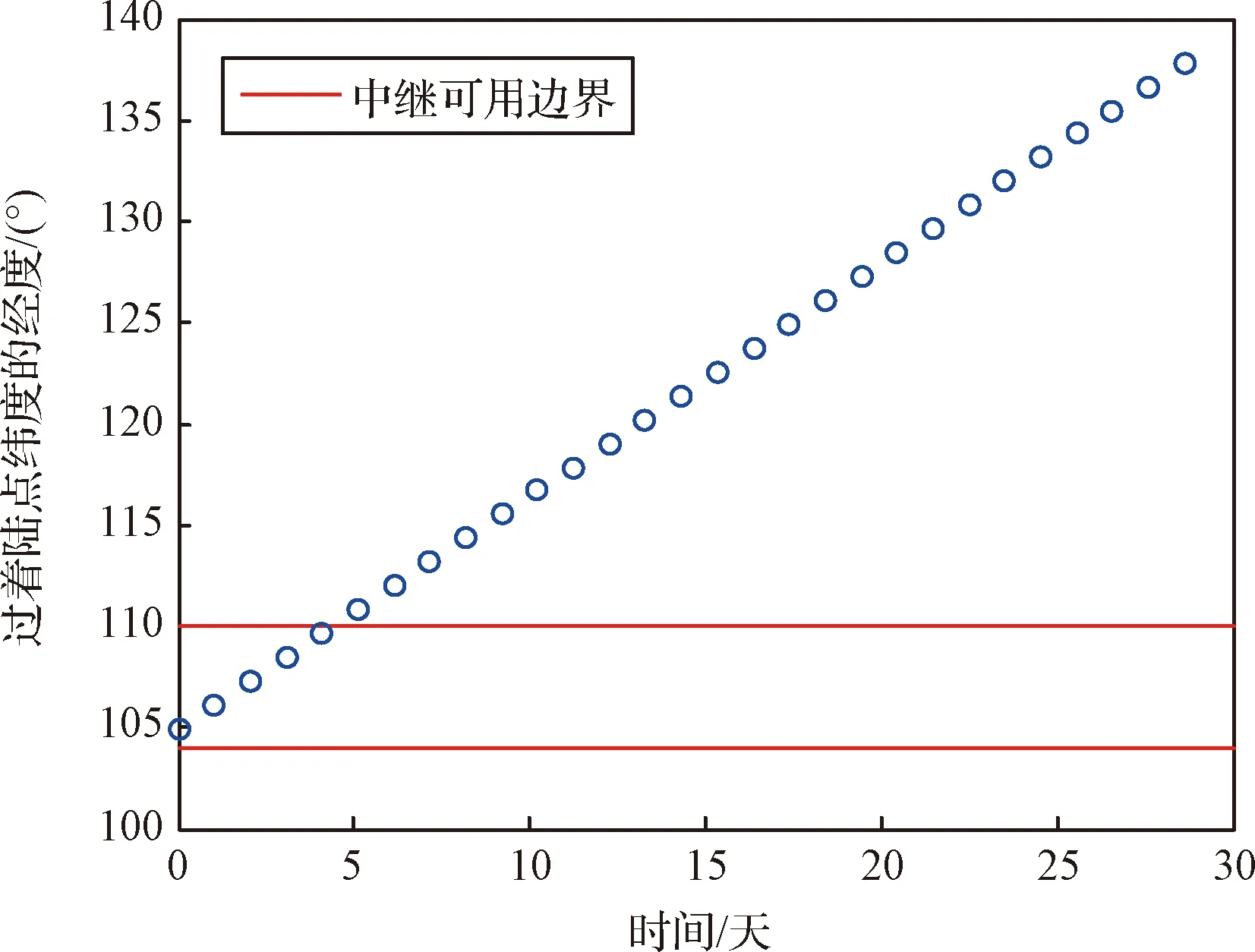
圖3 僅考慮非球形攝動J4項時,環繞器過著陸點緯度的經度隨時間變化Fig.3 Variation of the orbiter’s longitude passing the latitude of landing site over time when only considering non-spherical perturbation J4

可以看到,在火星主要非球形攝動項下,環繞器星下點過著陸點緯度時的經度呈現出單調遞增的趨勢,跟實際情況完全不同。根據對式(1)中非球形攝動主要帶諧項的攝動影響進行分析可知,環繞器軌道半長軸、偏心率與傾角的平根保持不變,升交點赤經與近火點幅角的平根長期項線性變化,而這種軌道變化不會導致過著陸點緯度的經度表現出圖2先變大再變小的特性。因此,一定是其他某個在軌道設計中通常并不被考慮的攝動項,起到了決定性的作用。本文將對該問題進行深入研究,可以為后續火星環繞探測任務軌道設計提供重要參考。

2 攝動分析

2.1 關鍵攝動項分析

首先分析不同的攝動力模型下,中繼軌道星下點過著陸點緯度時的經度隨時間變化情況,從而找出導致中繼漂移現象的主要攝動因素。

考慮全攝動模型和,非球形攝動模型。全攝動模型與上文一致,,非球形攝動模型僅采用JGMRO 120 d火星引力場模型,和表示考慮的最高階數和次數,如模型(即通常所說的)表示考慮了,和項。不同攝動模型下隨時間變化情況如圖4所示。

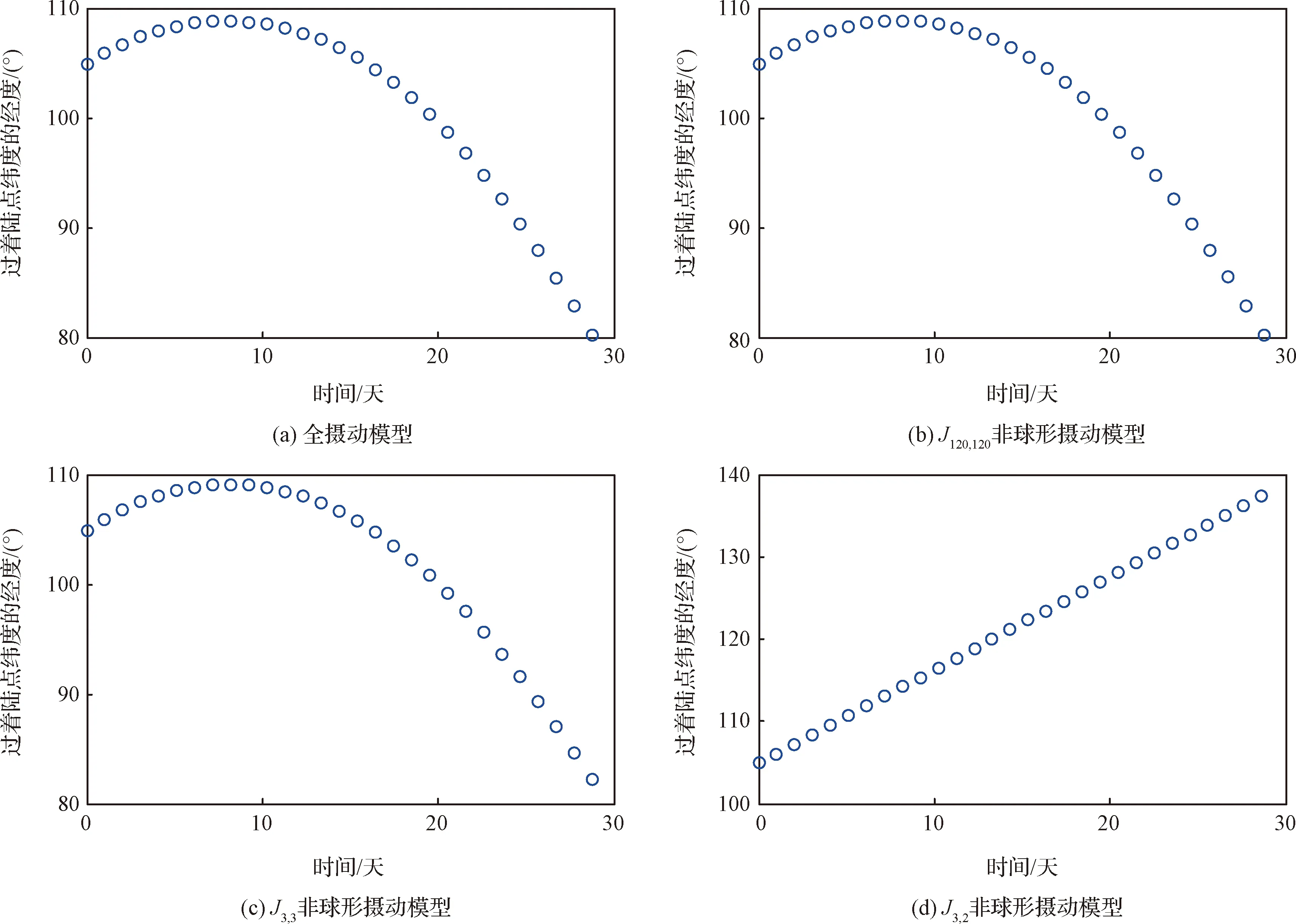
圖4 不同攝動模型下中繼軌道星下點過著陸點緯度時的經度隨時間變化Fig.4 Variation of the orbiter’s longitude passing the latitude of landing site over time under different perturbation models

從圖4(a)和圖4 (b)可以看出,火星非球形攝動在中繼軌道漂移中起到主要作用；從圖4 (c)和圖4 (d)可以看出,考慮非球形攝動模型時星下點漂移特性仍然與真實情況保持一致,但是當考慮非球形攝動模型時星下點漂移特性發生了明顯變化,出現了完全不同的漂移規律。因此,從圖4中可以初步得出結論,3階3次田諧項是導致星下點漂移特殊現象的主要因素。

2.2 軌道根數攝動分析

下面分別對非球形攝動模型和非球形攝動模型對軌道根數的攝動進行分析。

從圖5到圖8可以看出,非球形攝動仍然主要體現著帶諧項攝動的主要特征,即平均軌道根數下的半長軸、偏心率、軌道傾角幾乎保持不變；非球形攝動下,軌道根數變化趨勢發生了明顯變化：30天內半長軸隨時間明顯增大；偏心率變化趨勢也與下相反,但是從近火點高度升高的更快來看,半長軸與偏心率這兩個描述軌道形狀的根數中,半長軸起到更為主導的作用；軌道傾角隨時間明顯減小；升交點赤經與非球形攝動稍有偏差,主要是由于半長軸的變化導致升交點赤經漂移率發生了變化；近火點幅角變化與非球形攝動基本一致。

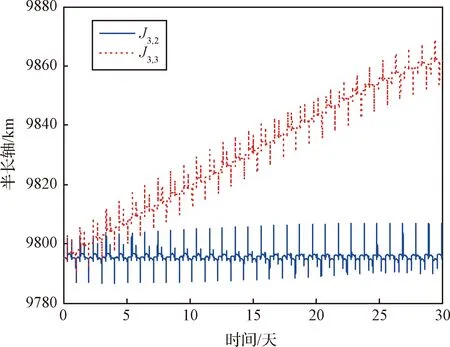
圖5 平均半長軸受攝變化Fig.5 Change of mean semimajor axis under perturbation

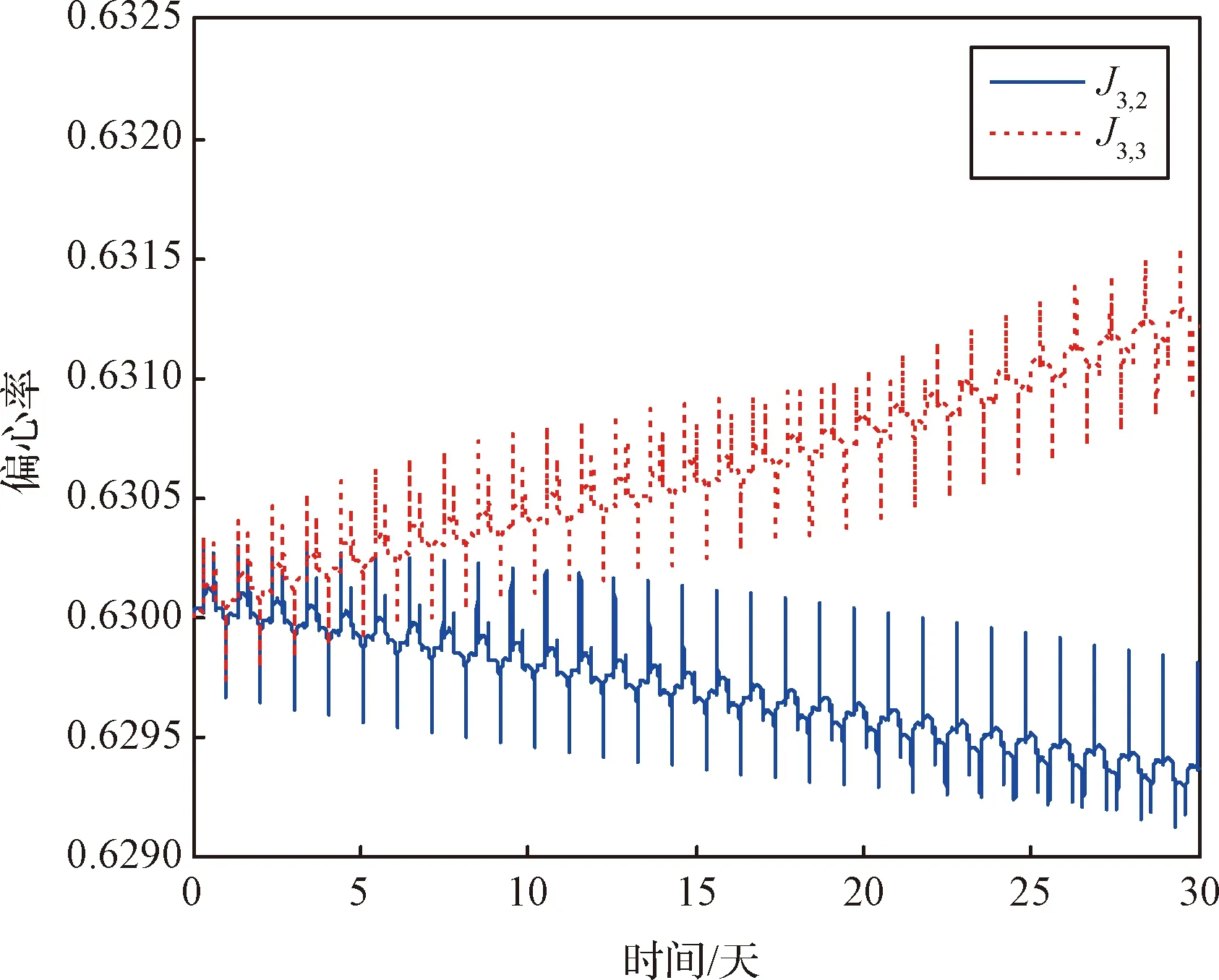
圖6 平均偏心率受攝變化Fig.6 Change of mean eccentricity under perturbation

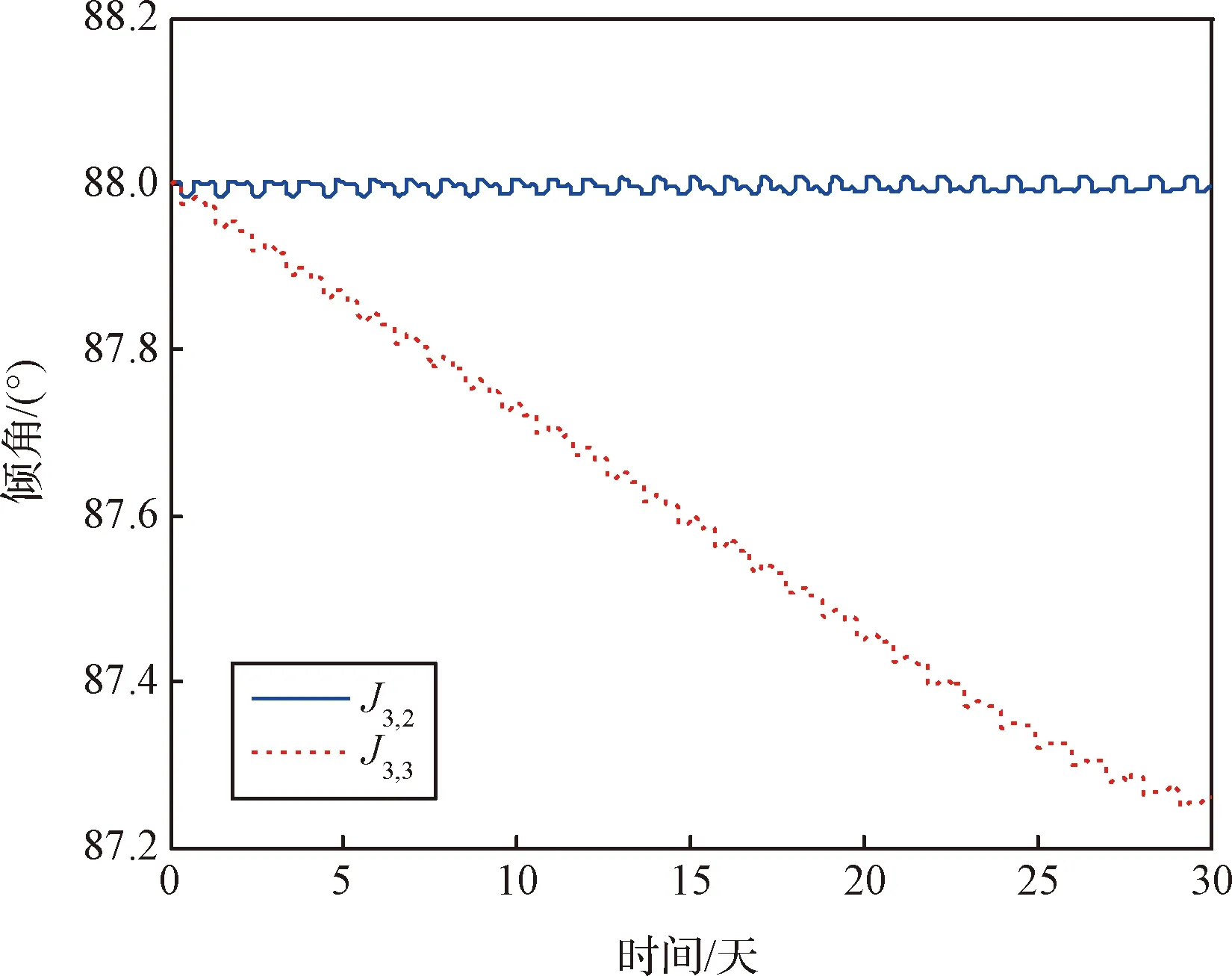
圖7 平均傾角受攝變化Fig.7 Change of mean inclination under perturbation

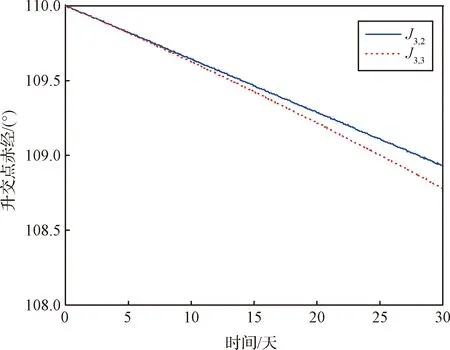
圖8 平均升交點赤經受攝變化Fig.8 Change of mean RAAN under perturbation

通過比較與非球形攝動下軌道攝動的差異,可以初步認為,中繼軌道漂移特性是由非球形攝動導致的半長軸增大或者軌道傾角減小導致,具體原因將在下文進一步分析。

3 λφ簡化計算與漂移原因分析

3.1 λφ簡化計算方法

為了進一步分析中繼軌道星下點過著陸點緯度時的經度漂移特性的原因,需要對進行簡化計算,從而可以對不同變量進行剝離,找到漂移特殊現象的主要因素。

首先需要計算過指定緯度圈的交點周期。圖9中指定緯度圈的緯度為,表示沿衛星運動方向從標準緯度圈起量的角度,表示沿衛星運動方向從升交點到指定緯度圈的角度,根據圖有：

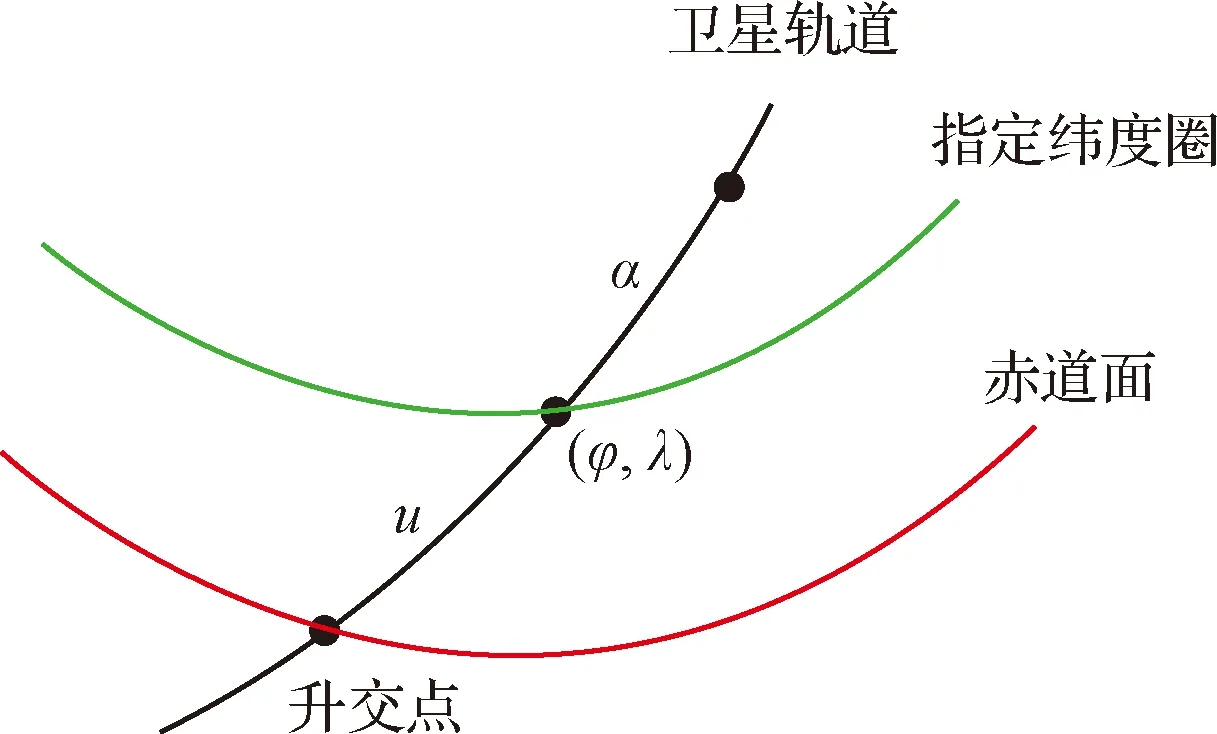
圖9 星下點過指定緯度圈示意圖Fig.9 Diagram of the sub-satellite point crossing a specified circle of latitude

+=+

(2)

式中：表示真近點角。

因此,計算變化一周的時間,即可得到,即有：

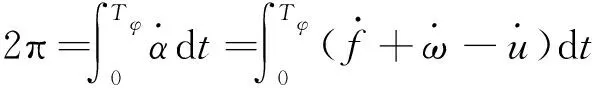
(3)

在約一個軌道周期的時間內,可以將軌道根數的變化率近似為常數。真近點角可以通過平近點角來求得：

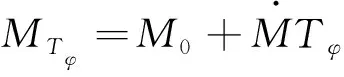
(4)

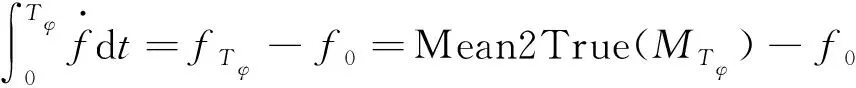
(5)

式中：Mean2True表示平近點角與真近點角的轉換,具體過程可參考文獻[20]。

根據球面三角形,有：

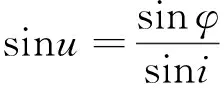
(6)

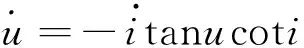
(7)

因此可以通過數值的方法求解交點周期,即求解以下方程：

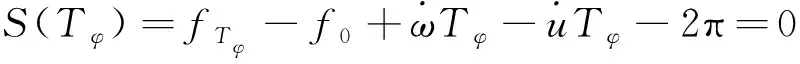
(8)

該方程可以使用軌道周期作為初值簡單快速求解。

求得交點周期后,即可再通過火星自轉角速度和軌道升交點赤經漂移速度,求得過指定緯度的經度漂移Δ：

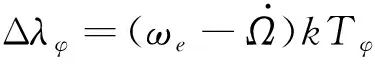
(9)

式中：表示火星自轉角速度,表示軌道圈數。

對于攝動情況,軌道根數的變化率見公式(1),利用上述方法可以求得的估計值,并且將其與實際軌道積分計算下得到的實際值進行比較,結果如圖10所示。

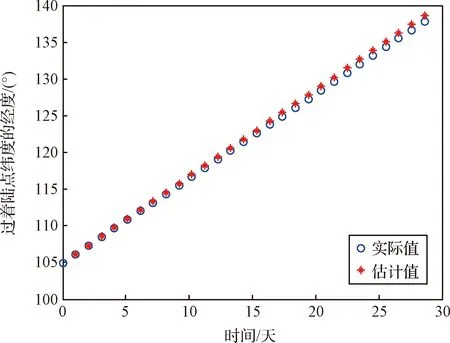
圖10 J4攝動下過給定緯度時的經度比較Fig.10 Comparison of the longitudes passing a specified latitude under J4 perturbation

從圖10中可以看出,的簡化計算方法具有較高的精度,后續可以使用該方法計算并進行分析。

3.2 λφ漂移原因分析

根據上一節結果,待進一步分析確定漂移特性是由非球形攝動導致的半長軸增大引起,還是軌道傾角減小引起。

為了簡化分析,根據圖5中非球形攝動對平均軌道根數的攝動結果,假設半長軸和傾角在30天內約為線性變化,其變化表達式為：

()=+Δ

(10)

()=+Δ

(11)

式中：Δ=2.5 km/天,Δ=-0.0246°/天,表示軌道漂移時間。

使用簡化計算方法,在攝動帶來的軌道根數變化基礎上,再分別根據上式考慮半長軸的增加和傾角的減小,再來看的變化情況。

從圖11中可以看到,只有當半長軸增大時,呈現出了與真實情況一致的變化特性,軌道傾角的減小并不會導致該特性。

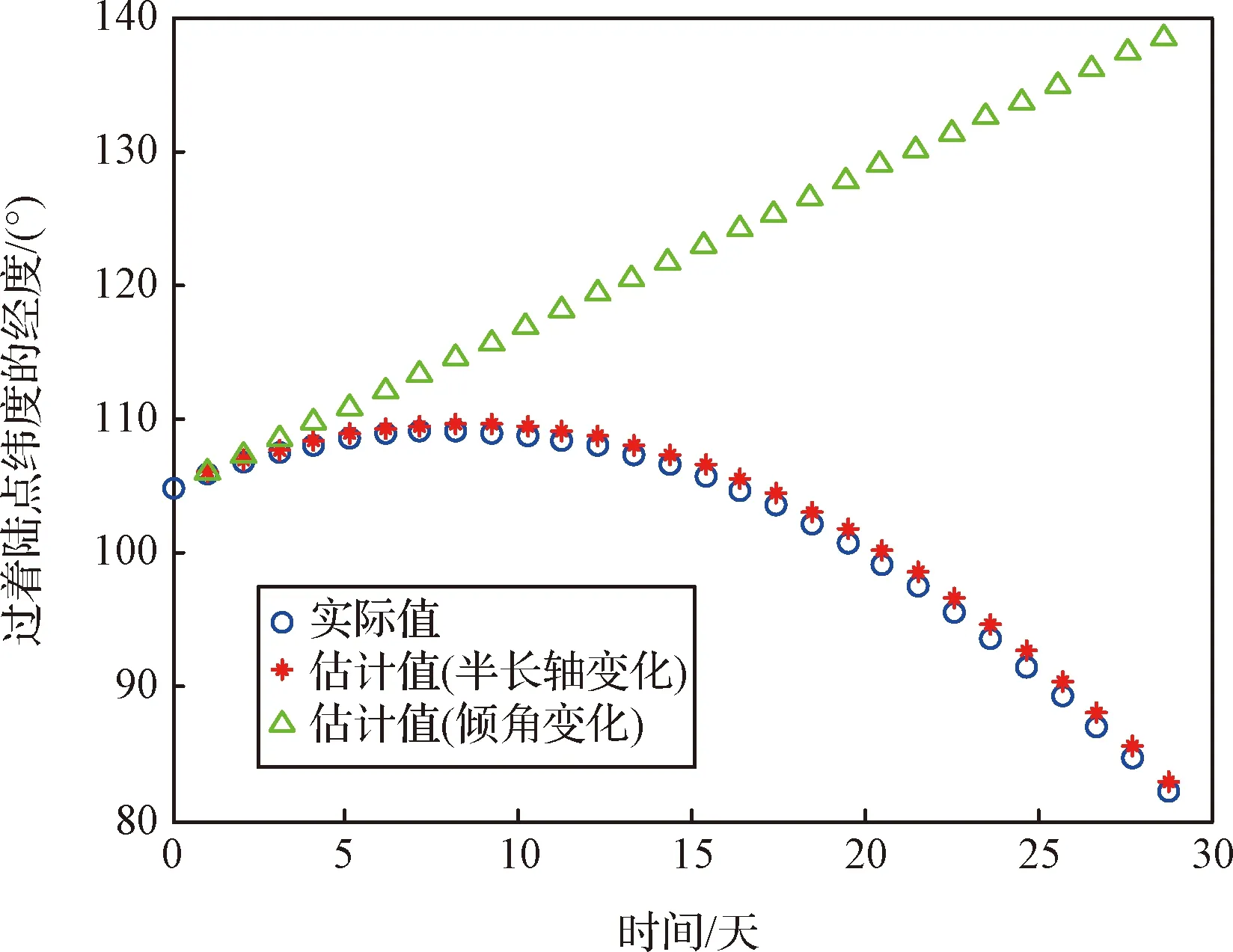
圖11 不同軌道變化下過給定緯度時的經度比較Fig.11 Comparison of the longitudes passing a specified latitude under different orbital changes

通過以上一系列數值實驗,可以得到如下結論：田諧項非球形攝動引起的軌道半長軸增大,是先增大再減小的主要因素。由于帶諧項使得單調增大,因此可以認為初期的增大主要是由帶諧項引起；半長軸增大會使得軌道周期變長,導致減小,因此可以認為隨后的減小是半長軸增大導致的。

但是,田諧項攝動為何會導致半長軸增大,仍需要進一步分析。

4 軌道受攝共振

考慮非球形攝動的中心天體引力場位函數可以寫成以下形式：

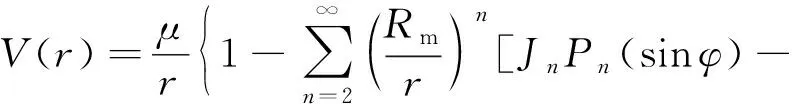
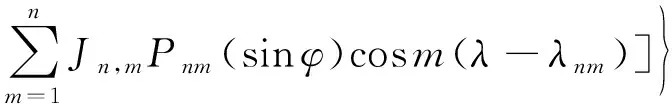
(12)

式中：,,分別表示衛星距中心天體質心的距離、經度和緯度。其中：

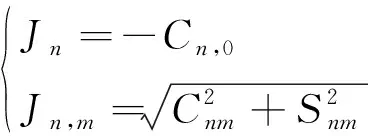
(13)

(14)

其中,與是通過測量得到的一組引力位系數,一般可以直接由描述非球形引力場的模型給出。對于=0下的系數,即(,0),其特征與經度無關,稱為帶諧項系數；對于>0下的系數,即,(,),其特征與經度有關,稱為田諧項系數。

,是勒讓德多項式,其中對于軌道設計中一般會考慮的4階帶諧項有：

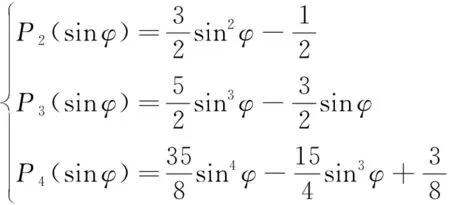
(15)

而對于田諧項有：

(16)

關于帶諧項攝動的研究已經較多,本文將針對上文分析得出結論的關鍵攝動項非球形攝動展開深入分析。項的引力場位函數可寫為：

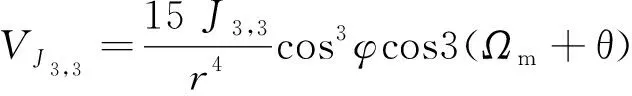
(17)

其中

+=-

(18)

=-[()+]

(19)

幾個角度的關系如圖12所示,和分別表示星下點經度和緯度,()表示火星固連系軸與慣性系軸的夾角,表示升交點經度與的角度差,表示星下點經度與升交點的角度差。從圖中關系以及球面三角公式,有：

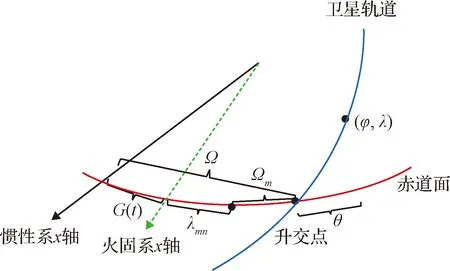
圖12 田諧項相關角度關系示意圖Fig.12 Diagram of the tesseral harmonics perturbation related angles

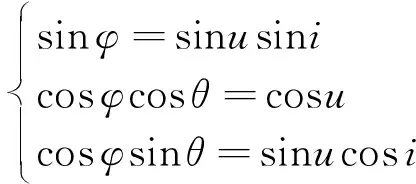
(20)

式中：=+。因此用軌道根數描述的項引力場位函數可以寫為：

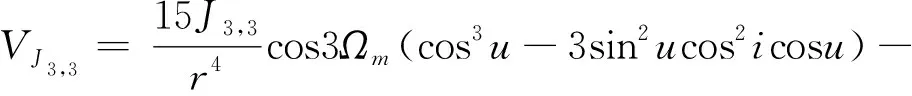
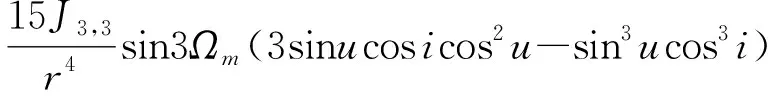
(21)

將該公式進行進一步推導,結合三角公式：

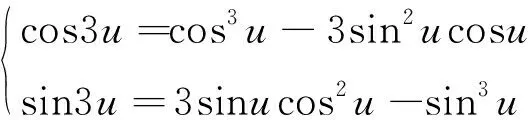
(22)

可得:

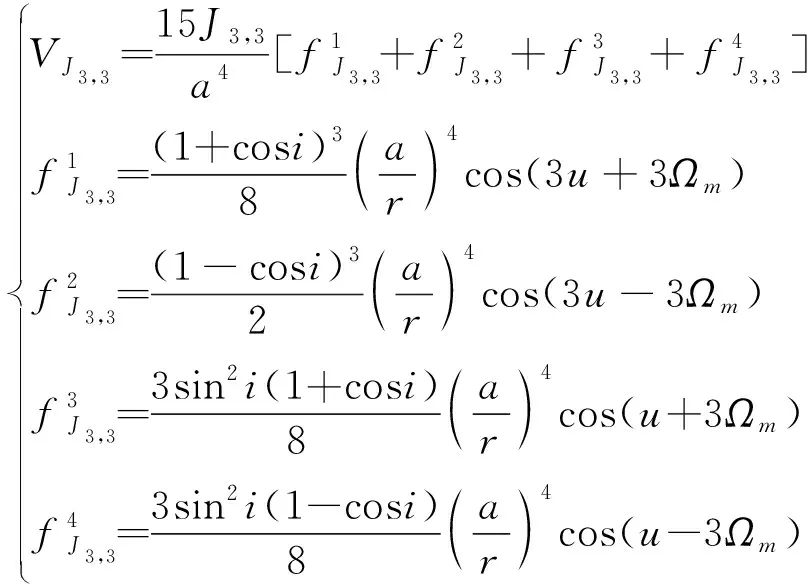
(23)

根據拉格朗日攝動方程可知,半長軸的變化率與引力場位函數對平近點角的偏導數相關,因此可以將引力場位函數對平近點角求偏微分,再對時間進行積分,即可得到半長軸變化的表達式。引力場位函數與平近點角的關系推導如下。

將和展成平近點角的三角級數,取到項的結果為：

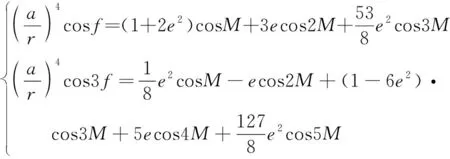
(24)

因此可以將項引力場位函數描述為平近點角的函數：

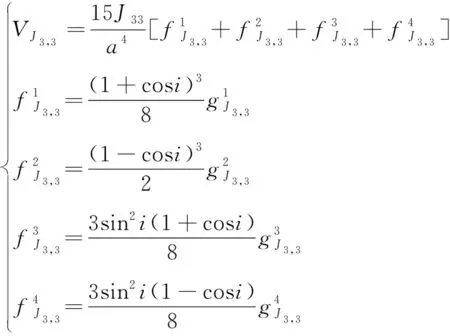
(25)

使用函數表示和展成平近點角的展開項,表達式為：

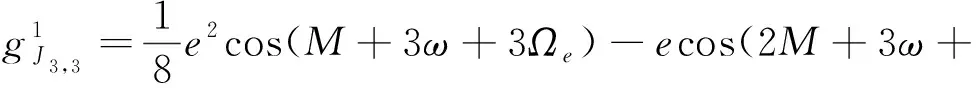
3)+(1-6)cos(3+3+3)+

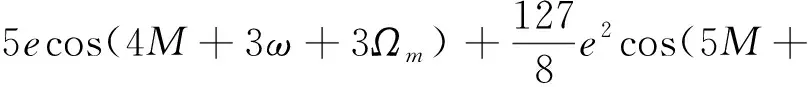
3+3)

(26)

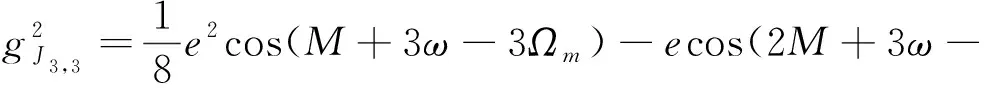
3)+(1-6)cos(3+3-3)+

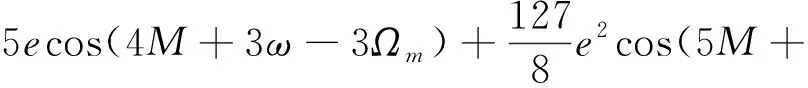
3-3)

(27)

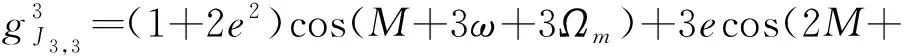
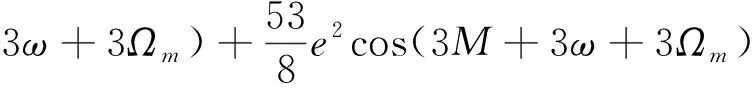
(28)

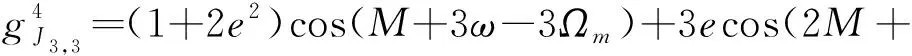
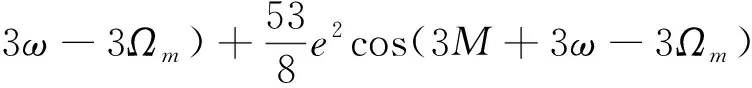
(29)

可以看到,平近點角描述的項引力場位函數可使用一基本函數單元描述：

=cos[+3(±)]

(30)

式中：=1,2,3,4,5,表示一整數。

則

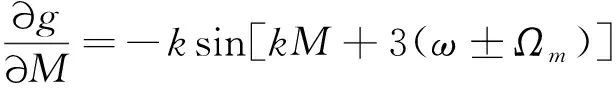
(31)

結合拉格朗日攝動方程：

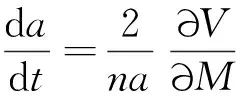
(32)

進而有：

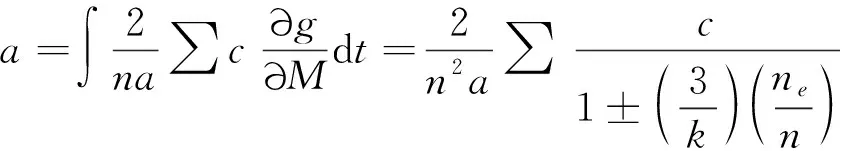
cos[+3(±)]

(33)

式中：為系數,為軌道運動平均角速度,為火星自轉角速度。從式中可以看到：

1)如果與正好成某個比例關系時,分母會出現等于零的情況,將會產生軌道共振,導致軌道半長軸顯著增大；

2)軌道半長軸的變化仍是周期性運動。

中繼軌道周期約為火星日的1/3,即/=1/3,通過以上計算可以得到,對于項攝動,當=1時,會導致半長軸出現小分母,進而產生軌道共振,從而在某段時間內表現為半長軸顯著增大的現象。

將軌道遞推時間設為365天,項與項攝動下的半長軸變化情況如圖13所示。可以看到,相比于攝動,項攝動會導致半長軸長周期運動有較為顯著的振蕩現象,這與上文推導所得到的軌道共振結論一致。一般工程任務在地球同步軌道設計時需要考慮田諧項帶來的東西漂移的影響,而對于非同步軌道很少考慮田諧項的影響,但是本文的分析結果表明非同步軌道上的環火衛星在軌道設計時也需要注意田諧項產生的軌道共振現象。同時可以看到,在前30天左右半長軸顯著增大,與前文分析中環繞器軌道半長軸在30天內增大的現象一致。環繞器進入中繼軌道后正好處于半長軸增大的階段,從而最終導致了過著陸點緯度時的經度出現先增大再減少的現象。

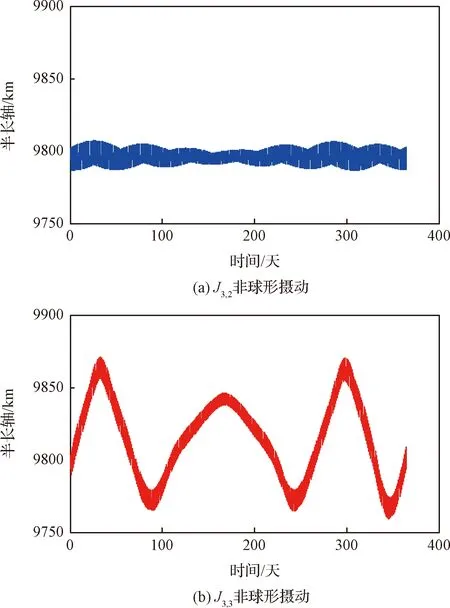
圖13 365天內半長軸受攝變化Fig.13 Changes of semi-major axis under perturbation within 365 days

5 結 論

本文對環繞器中繼軌道星下點過著陸點緯度時的經度先增大再減小的特殊現象進行了分析。通過一系列數值分析,結合星下點過著陸點緯度時經度的簡化計算方法,找到了火星非球形攝動田諧項導致的軌道半長軸增大是產生該特殊現象的主要原因。進一步,通過對田諧項引力場位函數進行推導分析,發現當中繼軌道周期約為火星日的1/3時,田諧項會產生軌道共振,從而使得半長軸長周期運動有著較為顯著的振蕩現象,在某段時間內表現為半長軸顯著增大。工程中一般僅在同步軌道衛星設計上會考慮田諧項的影響,但是本文進一步發現了田諧項對非同步軌道上的環火衛星也可以產生較為顯著的軌道共振現象,可以為后續火星環繞探測任務軌道設計提供重要參考。