福建省私人汽車擁有量預測
——基于灰色GM(1,1)模型的研究
時秀娟
(仰恩大學 數學系,福建 泉州 362014)
自1985年鄧聚龍提出GM(1,1)模型(1 階方程和1個變量的灰色模型)以來,灰色GM(1,1)模型被廣大學者從不同角度進行了深入研究[1],并已被廣泛應用于經濟、生產、生態及工程等領域的預測之中。
近年來,我國私有汽車的擁有量不斷增加,隨之而來的交通安全及環境污染等問題也不斷增加。
私有汽車擁有量及其增長情況,是城市建設及交通治理的重要理論基礎。本文用灰色GM(1,1)模型預測福建省私人汽車擁有量的增長情況,以期為福建省的城市建設、道路規劃及交通治理等提供科學的理論依據。
一、GM(1,1)模型簡介[2]
設原始數列為:
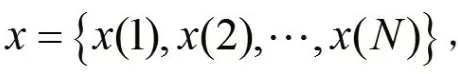
其中稱為原始數據,構造數列
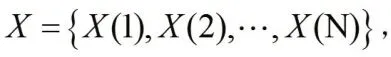
其中
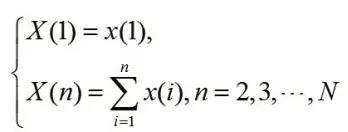
稱X為累加生成數列,X(n),n=1,2…稱為累加生成數據,X具有弱隨機性。
GM(1,1)模型對應的微分方程為:
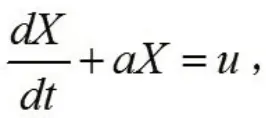
求解得
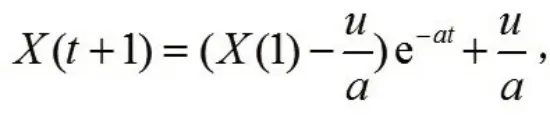
離散取值時得到累加生成數據的模型值
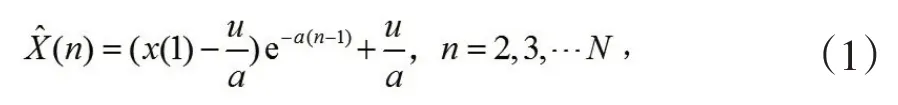
其中

由生成數據還原,得原始數據模型值

二、GM(1,1)模型在福建省私人汽車擁有量預測中的應用
利用表1中數據,可得:

表1 福建省私人汽車擁有量(單位:萬輛)
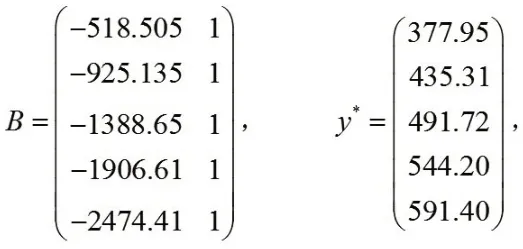
將上述兩矩陣代入式(2)可求得a=-0.816,u=331.2081,再由(1)式可得預測模型為:
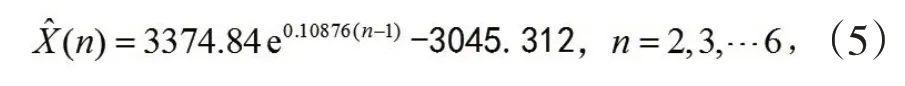
進一步由(4)式及(5)式可得預測值表2:
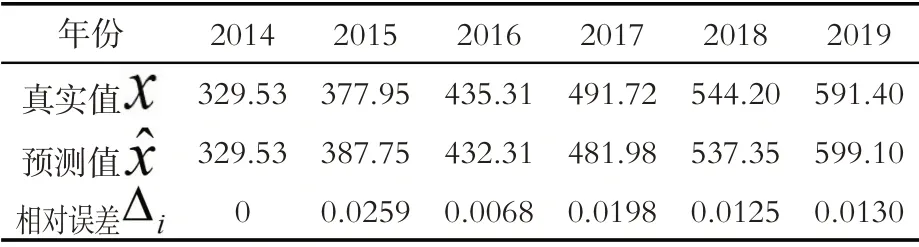
表2 福建省私人汽車擁有量預測值(單位:萬輛)
三、GM(1,1)模型的精度檢驗
為了對模型進行檢驗,首先給出模型檢驗等級[4]:
表中符號說明:
平均相對誤差:
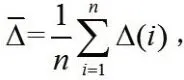
均方差比值:
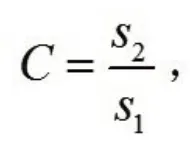
小誤差概率:
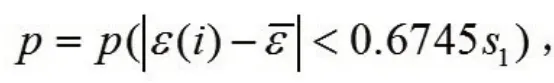
根據表2可得福建省私人汽車擁有量預測值的殘差和相對誤差表4:

表4 福建省私人汽車擁有量預測殘差和相對誤差
根據表2和表4中所求數據,對模型做如下檢驗。
(1)平均相對誤差:
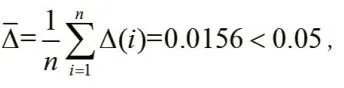
由表3可知模型的預測精度為二級。
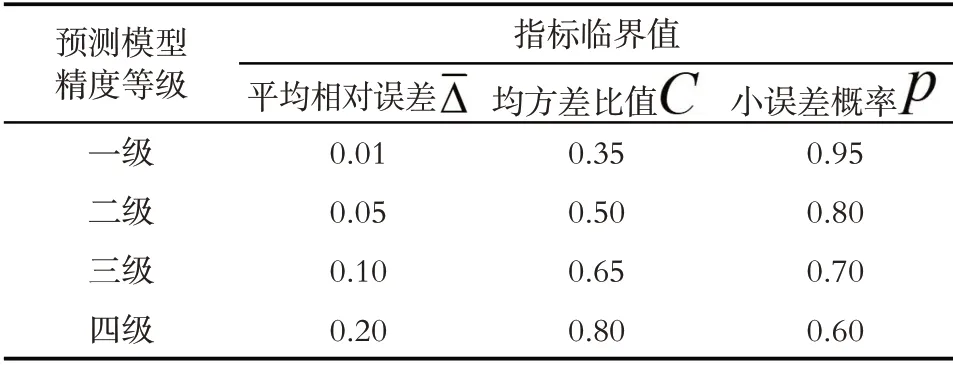
表3 模型精度等級劃分標準
(2)均方差比值C:
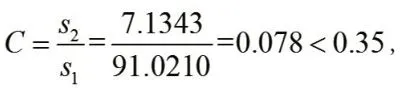
由表3可知模型的預測精度等級為一級。
(3)小誤差概率P:
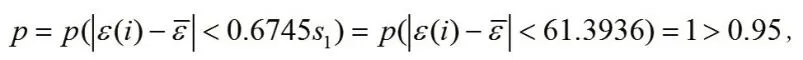
由表3可知模型的預測精度等級為一級。
上述三種檢驗模型的平均相對誤差為二級;均方差為一級;小誤差概率為一級。因此GM(1,1)模型為合格預測模型,通過此模型計算可得出,福建省未來5年私人汽車擁有量的預測值分別為667.93,744.67,830.20,925.63,1031.97(單位:萬輛)。
結論
用灰色GM(1,1)模型計算簡便、模擬結果精度較高、應用性強。通過計算,發現福建省私人汽車擁有量未來五年的增長趨勢并沒有減緩。

