聚焦數(shù)學(xué)核心素養(yǎng) 優(yōu)化研究性學(xué)習(xí)教學(xué)
——以“一道中考數(shù)學(xué)題”為例

云南省廣南縣珠琳鎮(zhèn)初級中學(xué)校 黎占金

1 試題呈現(xiàn)

如圖1(2020·四川涼山)，一塊材料的形狀是銳角三角形ABC，邊BC=120 mm,高AD=80 mm,把它加工成正方形零件，使正方形的一邊GH在BC上，其余兩個(gè)頂點(diǎn)E,F分別在AB，AC上，求這個(gè)正方形零件的邊長.

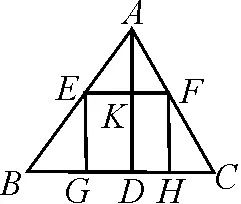
圖1

2 精心設(shè)計(jì)，巧妙點(diǎn)撥和引導(dǎo)，拓展發(fā)散思維

在解題教學(xué)中，巧妙設(shè)計(jì)啟發(fā)式設(shè)問與反問，安排自主、合作、探討式的研究性學(xué)習(xí)活動，鼓勵(lì)學(xué)生從不同角度來研究解題思路，有利于培養(yǎng)學(xué)生思維的廣度與深度.在此題的解題教學(xué)中，教師精心設(shè)計(jì)問題，巧妙點(diǎn)撥和引導(dǎo)，經(jīng)學(xué)生探討研究，歸納出以下幾種解法.

活動一：根據(jù)三角形相似的性質(zhì)1求解.

師：此題圖形中有沒有相似的三角形？

生1：有的.如△AEF∽△ABC.

師：在相似三角形的性質(zhì)中，相似三角形哪些線段的比等于相似比？此題可以用什么線段的比等于相似比求解？

生2：相似三角形對應(yīng)高的比、對應(yīng)中線的比、對應(yīng)角平分線的比、周長的比都等于相似比.

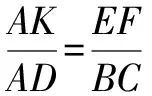
活動二：應(yīng)用探索研究得出的結(jié)論求解.

師：當(dāng)兩個(gè)三角形相似時(shí)，對應(yīng)的什么量相等？對應(yīng)的什么量成比例？

生4：對應(yīng)角相等，對應(yīng)邊成比例，對應(yīng)邊的比就是相似比.

師：在圖1中，除△AEF∽△ABC外，還有類似的相似三角形嗎？

生5：有的，如△BEG∽△BAD,△CFH∽△CAD.

師：很好！請同學(xué)們試著寫出△AEF∽△ABC和△BEG∽△BAD這兩組相似三角形之間有關(guān)系的兩組成比例的對應(yīng)邊.

生6：因?yàn)椤鰽EF∽△ABC，所以

①

因?yàn)椤鰾EG∽△BAD, 所以

②

師：把①②式的左右兩邊分別相加后，再結(jié)合題圖觀察，有沒有新的發(fā)現(xiàn)？

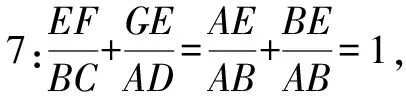
師：好極了！應(yīng)用此結(jié)論，此題也可得解.

活動三：應(yīng)用等面積法.

師：還記得三角形、梯形、正方形的面積公式嗎？

生8：記得.三角形的面積等于底乘高除以2；梯形的面積等于上底加下底的和乘高再除以2；正方形的面積等于邊長的平方.

師：此題圖中△ABC的面積可分成哪些規(guī)則圖形面積的和？

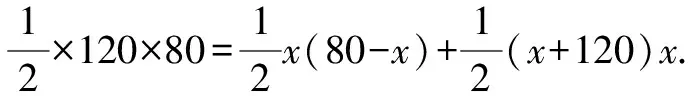
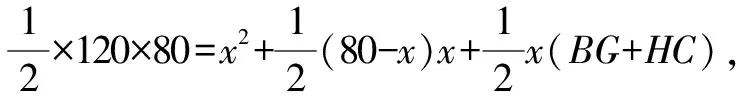
活動四：應(yīng)用三角形相似的性質(zhì)2求解.

師：相似三角形性質(zhì)2的內(nèi)容是什么？

生11：相似三角形周長的比等于相似比，面積的比等于相似比的平方.

師：此題能否用相似三角形面積的比等于相似比的平方這一性質(zhì)來求解？

3 深化拓展，變式研究

3.1 條件變式拓展

變式1把銳角△ABC變?yōu)橹苯侨切危螦=90°.能否求出正方形的邊長？

變式2把△ABC變?yōu)榈妊苯侨切危螦=90°.能否求出正方形的邊長？

變式3把△ABC變?yōu)榈冗吶切危疫呴L等于a，能否求出正方形的邊長？

拓展1把正方形EGHF變?yōu)榫匦危欠窨梢郧蟪鼍匦胃鬟叺拈L？若不能，需添加一些什么條件？(比如長與寬的比等.)

拓展2把△ABC的高AD變?yōu)榻瞧椒志€或BC邊上的中線，還可以求EF的長嗎？若不能，該怎樣變動其他的條件才可以求出EF?(比如把正方形EGHF變?yōu)槠叫兴倪呅危褽G∥AD.)

拓展3把△ABC變?yōu)殁g角三角形，正方形EGHF變?yōu)榫匦危€能求矩形各邊的長嗎？若不能，需添加一些什么條件才可以求解？

師：以上的6種變式拓展，能否用之前四個(gè)活動中的方法來求解？

生13：有的可以用活動一的方法求解.

3.2 圖形切割變換

(1)在圖1中，切割掉高AD右邊的部分.

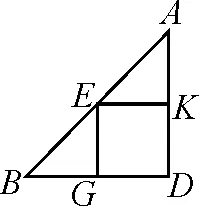
圖2

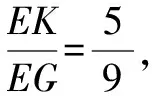
師：題圖經(jīng)過這樣的切割后，還能用之前的四種方法求解嗎？

(2)在圖1中，切割掉EF上面的部分.

已知梯形EBCF,EF∥BC,EF=48 mm,BC=120 mm,梯形的高為32 mm,求兩腰延長線的交點(diǎn)到下底BC的距離？

師：題圖經(jīng)過如此的截除，同時(shí)結(jié)論也隨之變換后，能否求解呢？

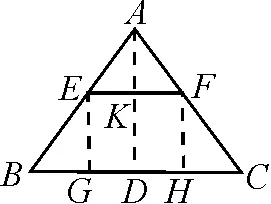
圖3

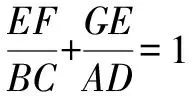
3.3 條件、圖形同源變換拓展

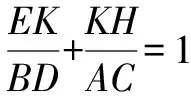
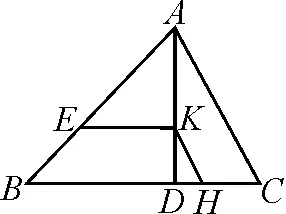
圖4

圖5

圖6

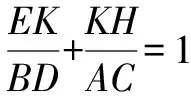
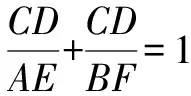
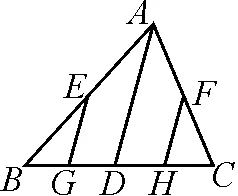
圖7

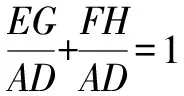
師：以上幾種同源變式和拓展，結(jié)論是否成立？若能成立，用之前哪一種活動的方法求解？

生17：每一種同源變式和拓展，結(jié)論都仍然成立.

生18：都可以用活動二的方法求解.

以上的變式和拓展都是以原題為著眼點(diǎn)，進(jìn)行了一些解法同源、結(jié)論歸一的探討，有利于學(xué)生對所學(xué)知識的條理化和系統(tǒng)化，培養(yǎng)了學(xué)生思維的廣度和深度.

3.4 題型的變式和拓展

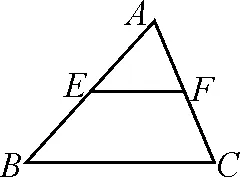
圖8

如圖8，已知在△ABC中，BC=5,AB=4,AC=3,EF∥BC.試問在BC上是否存在一點(diǎn)P,使△EPF為等腰直角三角形？若存在，試求出EF的長，若不存在，請簡要說明理由.

以本題型的變式和拓展是把原題進(jìn)行適當(dāng)?shù)刈儞Q，讓學(xué)生在不同的題型中體驗(yàn)多題一解和一題多解探究的樂趣，培養(yǎng)了學(xué)生思維的靈活性.解析略.

4 總結(jié)

在解題教學(xué)中，應(yīng)充分優(yōu)化并發(fā)揮解題的教學(xué)功能，將原題進(jìn)行適當(dāng)?shù)刈兪胶屯卣梗捎靡活}多解、一題多變、一圖多變、多題一解等訓(xùn)練，巧妙地點(diǎn)撥和引導(dǎo)學(xué)生進(jìn)行自主、合作、辯論、開放的探討和研究，讓學(xué)生最大限度地發(fā)揮出自己的聰明才智.通過優(yōu)化這種啟發(fā)式討論、開放式探究的研究性學(xué)習(xí)教學(xué)活動，不僅能提高學(xué)生的數(shù)學(xué)思維能力，也培養(yǎng)了學(xué)生的開拓創(chuàng)新精神，提升學(xué)生的數(shù)學(xué)核心素養(yǎng)，從而推動素質(zhì)教育的全面發(fā)展.