利用錯題資源 突破解題障礙

?蘇州工業園區景城學校 闕 成

1 引言

錯題是正解的先導，挖掘錯題的教學功能，充分發揮錯題的作用，是引領學生邁向成功的關鍵.不少教師都有這樣的體會：對于易錯點，雖反復強調，但就是有學生過不去這個坎兒，依然我行我素，出現類似的錯誤.究其原因，還在于教師沒能跟上新課改的步伐，不能及時更新教學觀念，導致學生無法從根本上糾錯.

學生出現錯題在所難免，而教師對待錯題的方式影響了學生各項能力的發展.正確、合理地挖掘錯題的教學功能，將錯題演化成教學的資源與契機，能拓寬學生的視野，有效地幫助學生擺脫學習的困境，提高學習效率.為此，筆者從自身的執教經驗出發，談幾點看法.

2 巧借錯題，培養符號意識

隨著初中數學中“數域”的擴大，不少學生的思維還停留在有理數范疇內用正數解決問題，對于實數中的負數還沒有建立符號意識.解題時，總會因運算符號問題導致錯誤發生.為了培養學生的符號意識，教師可有意識地利用錯題，幫助學生建構認知，避免同類錯誤的再發生.

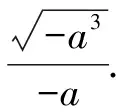
這是一道基礎題，看似簡單，學生的錯誤率卻很高，而且錯誤的方式還不一樣.若學生不能從根本上糾正錯誤，對初中乃至后期的數學運算能力的發展都會產生較大的負面影響.為此，筆者將此題作為教學資源，與學生一起分析，厘清出現錯誤的根源，讓學生在符號意識的生成下，獲得良好的運算能力.

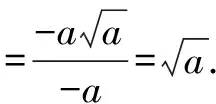
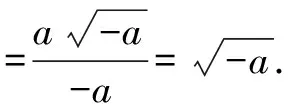
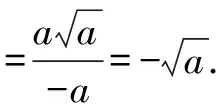
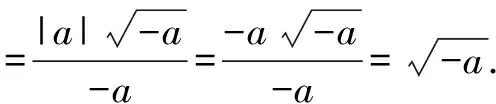
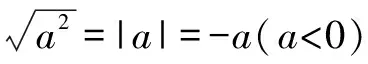
課堂是一個不斷發生變化的動態過程.遇到此題，作為一名有經驗的教師，就應該抓住這個契機，將本題變成本節課教學的有利資源，充分發揮本題的教學功能，這比學生后期花大量的時間刷題的效果更顯著.因此，教師可帶領學生先重溫絕對值化簡與二次根式的概念，在此基礎上，分別衍生出關于這兩個概念的習題，以鞏固學生對概念的理解.

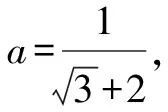
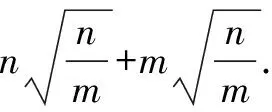
在一道錯題的引領下，教師充分利用這個資源帶領學生鞏固概念、拓展知識、衍生新題，讓課堂得以有效生成，從根本上糾正了學生的符號運算錯誤問題，有效地培養了學生的符號意識，為運算能力的形成與發展奠定了一定的基礎.

3 利用錯題，發展縝密思維

俗話說：“人非圣賢，孰能無過.”每個人都是在挫折與錯誤中不斷成長.初中階段學生的思維處于快速發展期，面對各種試題，難免會出現考慮不周或漏解的現象.因此，教師可充分發揮這些思維漏洞的教學功能，引導學生進行合理歸因，化錯誤為教學的利器，讓學生在這些錯誤中形成縝密的解題思路，使得錯誤綻放出別樣的光彩.

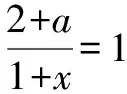
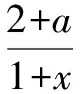
仔細觀察，發現出現這種錯解的學生并不是完全不會解本題，只是思維不夠嚴謹，考慮問題缺乏周全.此問題屬于學生思維與認知的范疇，因此教師可引導學生進行分步解題，以防止錯誤的發生.

正解分析：①去分母，化分式為整式.

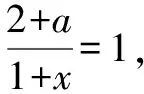
②移項，合并同類項.

則x=1+a.

③獲得滿足題意的a的一個條件.

由方程的解為非正數，得x≤0，也就是1+a≤0，因此a≤-1.

④重新審題，要使得分式方程成立，其分母不能為0.

由本題中的方程是分式方程，得1+x≠0，也就是x≠-1.

⑤匯總a的取值范圍.

由x≠-1得1+a≠-1，所以a≠-2.

綜上，a的取值范圍是a≤-1且a≠-2.

類似本題的錯誤在數學解題中時有發生，主要原因在于學生解題時容易遺漏一些隱含條件，而非不會解題.填補類似于此的思維漏洞，需要經歷一個漫長的培養過程.教師可鼓勵學生對問題進行分步思考，解完題時再回顧原題的條件，以防出現遺漏.只有將教學的著力點放在學生思維的生長點上，才能有效地幫助學生突破思維的局限性，實現錯題的最大化利用價值.

4 挖掘錯題，獲得解題思路

皮亞杰在建構主義學習理論中提出：“學習中，學習者總是習慣帶著自身原有的學習與生活經驗認識新的事物，倘若新知在原有認知經驗中缺乏參照，則會出現各種錯誤.”由此可見，錯誤的發生絕非偶然，而是建立在一定理論基礎上的必然產物.

解題中，部分學生遇到新的題型或沒有接觸過的問題，就會出現手足無措的狀態，解題過程毫無邏輯而言.遇到這種情況，教師可從細節方面點撥學生的思路，讓學生在教師的引導下結合自主探索獲得解題方法，這比教師完全呈現解題結論來得有效.

例3如圖1，已知點A與點B是兩坐標軸上的點，坐標分別為(a，0)，(0，b)，且a與b滿足a2+b2-12b-12a+72=0，CO∶AO=1∶3.

(1)分別求點A，B，C的坐標.

(2)若已知點D(1，0)，過點D的直線l與AB，CB分別交于點E，F，假設點E，F的橫坐標分別是xE，xF，當DB平分△EFB的面積時，求xE+xF的值.

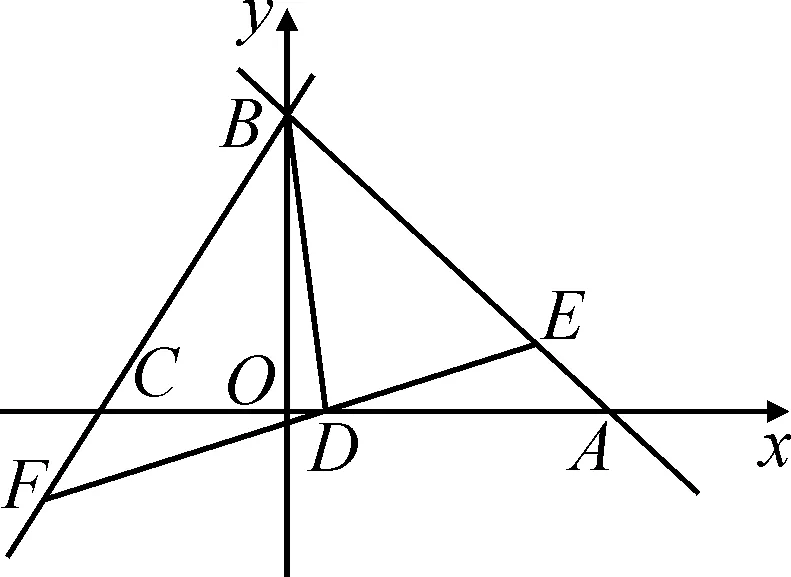
圖1

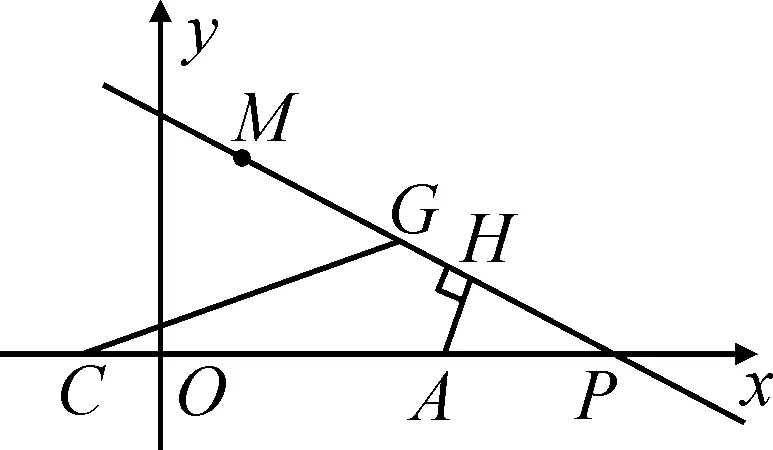
圖2

(3)如圖2，已知點M(2，4)，點P是x軸上位于點A右側的一個動點，AH⊥MP于點H，于PM上取一點G，使GH=AH，再連接GC.當點P在點A的右側運動時，∠MGC的度數會不會發生變化？若發生變化，請說明理由；如果不變，請求出∠MGC的值.

本題綜合型強，涉及的知識點比較多，對初中學生來說有一定的難度.問題梯度設計比較合理，第(1)問對所有學生來說，沒有什么難度，出錯率較低，而后面兩問則考查學生對基本圖形的理解.閱卷中，筆者發現學生在后兩問中的錯誤率比較高，故將此題特別拿出來與學生剖析，以幫助學生獲得良好的解題思維.

解決第(2)問的核心就是確定點D為線段EF的中點，只要找出“X”型，構造出△END≌△FMD(見圖3)，答案則很容易得到.

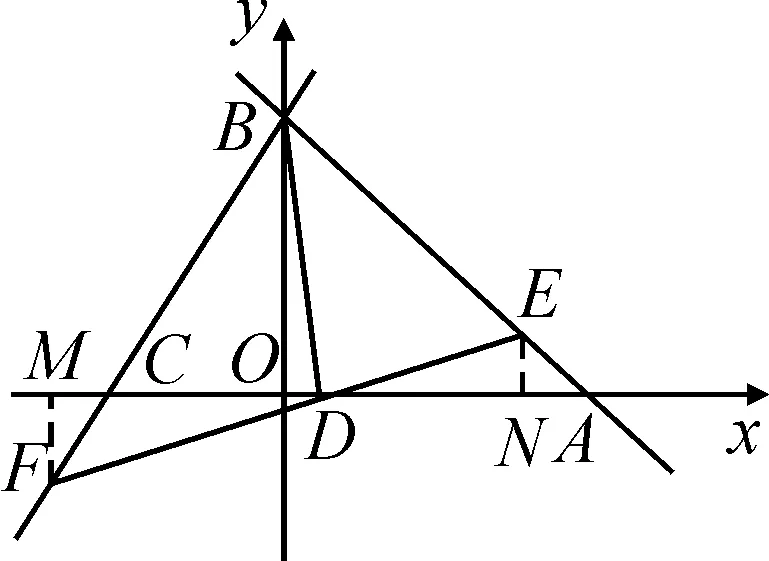
圖3

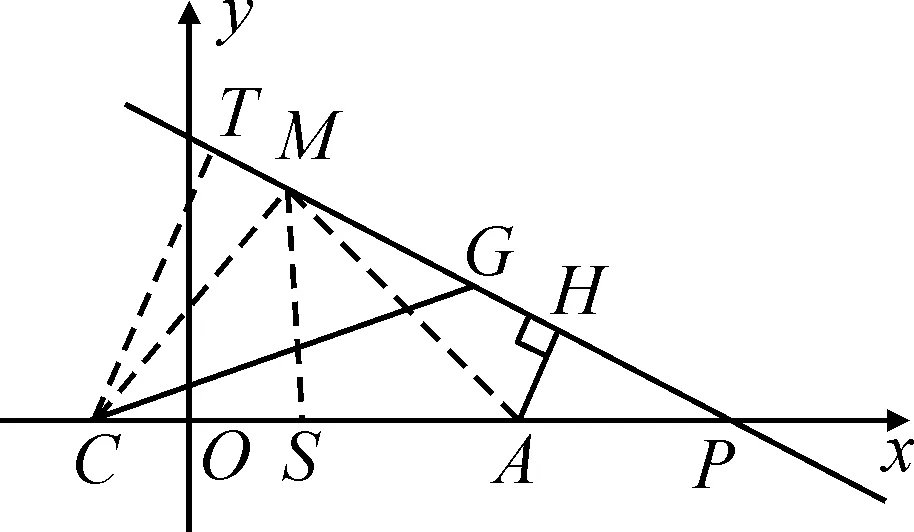
圖4

解決第(3)問的重點在于緊扣條件中點A，C，M的坐標，判斷從點M向x軸作的垂線的垂足為線段AC的中點，再依據“遇中點作垂線”的規則作出垂線段MS，再根據垂直平分線的性質，分別連接AM與CM，構造出等腰△CAM(見圖4)，再根據點的坐標證明△CAM為等腰直角三角形.

此時，進行整體觀察，作出最后一條輔助線TC，使CT⊥PM.這是常見的基本題型，我們只要證明△CGT是等腰直角三角形，問題就解決了.

在教師的點撥下，學生驚嘆“原來是這樣啊！”“我怎么就沒想到呢！”“貌似也沒有想象中的那么難嘛”……正所謂：“聽君一席話，勝讀十年書.”教師四兩撥千斤的指導，使得學生的解題思路變得豁然開朗，呈現出柳暗花明又一村的感覺.

由此，筆者不禁反思，既然一點就通，為什么面對試題時，還有那么多學生感到無從下手而錯誤百出呢？學生面對不完整的圖形，難道就想不到將圖形補充完整？與部分學生交流后發現，學生的解題障礙還在于缺乏解題技巧，遇到沒見過的試題處于一知半解的狀態，往往是知其然而不知其所以然.

因此，教師在發現學生出現完全找不到解題思路的試題時，可引導學生探索新的解題技巧.如，此題中解決后兩問的關鍵是找準垂直和中點、三個直角及CM=AM等條件，就能想到怎樣作輔助線將圖形補充成我們所熟悉的基本圖形，將問題回歸到我們熟悉的類型中，也就突破了解題的障礙.

5 結束語

出現錯誤是常有的事.修正錯誤、挖掘錯題資源，發展學生的數學綜合能力對課堂教學來說極其重要，對知識的鞏固、解題技巧的形成及思維能力的發展都具有重要意義.W