創設數學經典例題 拓展知識遷移思維
?山東省沂源縣第四中學 杜春蓮
1 引言
自古至今,創設和精選經典的例題是數學課堂教學不可或缺的重要環節.創設經典的例題不僅與數學學科的教學特點一脈相承,還可幫助學生對一些數學質疑情境進行建模,有事半功倍的效果.那么如何在教學過程中精選經典的數學例題呢?筆者結合多年的教學實踐,從創設數學經典例題、拓展知識遷移思維談談自己的一點感悟,不到之處,還望同仁斧正.
2 創設具有層次性的例題,讓學生的思維隨知識由淺入深進行拓展
眾所周知,每個人的認知水平和智能水平都是千差萬別的.課堂教學針對的是一個群體,但落實的是學生個體,這就需要因材施教.同樣,初中生的思維逐漸由形象思維向抽象思維轉變,這一過程是循序漸進的.因此,創設具有層次性的例題,讓學生的思維隨知識由淺入深進行拓展,是提升課堂效率的有效途徑.如何做到創設具有層次性的例題呢?筆者在教學實踐中經常采用的方法是:第一,將例題根據質疑情境創設多個設問角度,設問的難度呈現遞進趨勢,讓學生的思維隨知識的深化而拓展;第二,對一節課中例題的知識難易程度進行有層次的設置,根據課堂教學的內容需要,精選不同層次的題目,精準其知識、方法和能力的構建方向,讓學生的遷移思維不斷地向前邁進.
例如,為了幫助學生鞏固平行線的性質,筆者將2020年江蘇省宿遷市中考數學卷的第4題進行變式:
案例1原題:如圖1,直線a,b被直線c所截,a∥b,∠1=50°,則∠2是多少度?
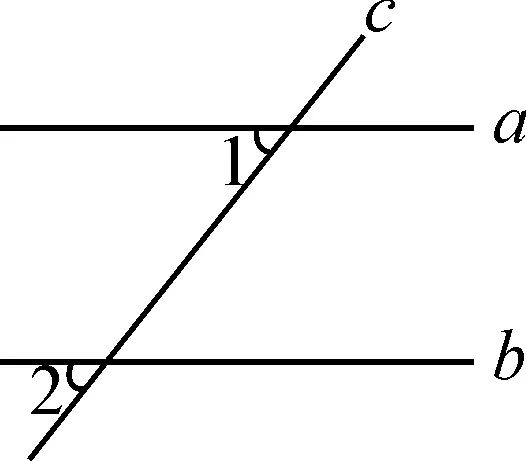
圖1
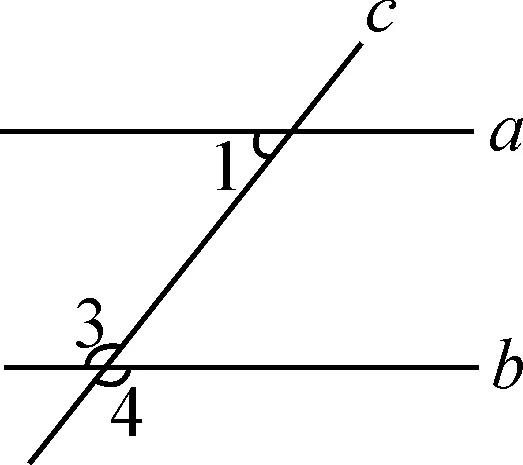
圖2
變式(1)如圖2,直線a,b被直線c所截,a∥b,∠1=50°,則∠3,∠4是多少度?
(2)如圖2,直線a,b被直線c所截,a∥b,∠1=α,則∠2是多少度?
(3)如圖2,直線a,b被直線c所截,a∥b,∠1=α,則∠3,∠4是多少度?
另一方面,對例題的難易程度進行有層次的設置,這是針對學生思維與知識差異的一種有效方法.比如,筆者對平行線性質的應用編排了A,B,C三個層次的例題:
案例2A層(基礎題):如圖3,直線a,b被直線c所截,已知∠1=∠2.求證a∥b.
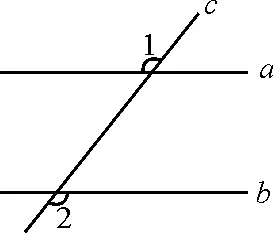
圖3
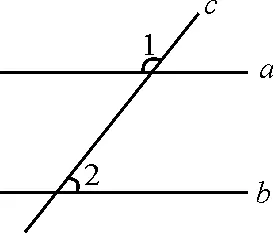
圖4
B層(中檔題):如圖4,直線a,b被直線c所截,已知∠1+∠2=180°.求證a∥b.
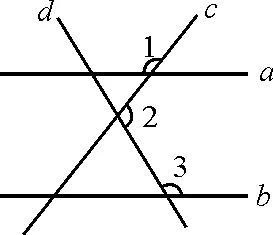
圖5
C層(拔高題):如圖5,直線a,b被兩條相交直線c,d所截,已知∠1+∠2+∠3=360°.求證a∥b.
創設目的:案例1中,利用中考試題作為平行線性質的母題,可以讓學生明確中考的考向,認識該知識的重要性,然后通過變式中的三個問題,從多角度對平行線的性質加以理解,舉一反三,從而達到對類似問題進行數學建模的目的.案例2中,則通過“平行線性質的應用”的不同難度的層面設置,滿足不同能力水平學生的需要,A層僅涉及邏輯思維推理,而B,C層則包含了數形轉換的思想,難度明顯加大,可以讓學生在已有的認知水平上都有所獲,思維得到發展.
3 創設具有多種解題方法的例題,讓學生的思維隨知識相互滲透進行拓展
根據多年的教學實踐經驗,初中數學教師必須有計劃、有意識地創設課堂教學環節,引導學生感受知識點之間的滲透,幫助他們構建初中數學體系,創設具有多種解題方法的例題,不斷地提高學生解決問題的能力,從而讓學生的思維隨知識相互滲透進行拓展.在創設例題時,需要留心那些可以采用多種途徑完成的典型例題,引導學生不拘一格地釋疑思路,激發他們舉一反三、敢于創新的探究潛能.可以通過分組比賽的形式,讓學生在不同的釋疑過程中比較優劣,提煉最佳的解題方法.
例如,在一元二次方程應用的教學中,筆者在傳授知識內容之后留給學生這樣一道例題:
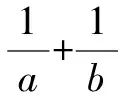
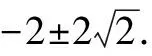
由此可以看出,通過小組討論,不僅能調動學生參與活動的激情,也能通過釋疑方法比較激發學生求知的欲望,從而獲得最優解題思路,為相似的數學質疑情境建模.
4 創設具有延伸性的例題,讓學生的思維隨知識歸納建模進行拓展
初中生有強烈的求知欲望,恰當的教學方法能挖掘出他們的潛能,從而激發他們質疑、探疑和釋疑的斗志.因此,教師必須注意在教學過程中不能以題論題,需要對知識進行恰如其分地拓展、延伸,從而讓學生對所學知識能舉一反三.
例如,在進行軸對稱圖形的教學時,筆者設計了這樣的教學例題:
案例4如圖6,直線l同側有兩點A,B,在直線l上找出一點使其到點A,B的距離之和最短.

圖6
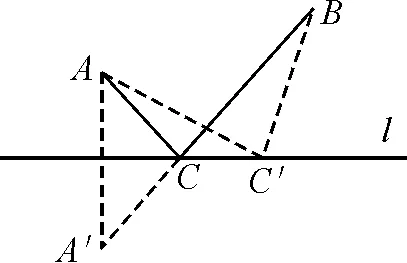
圖7
解析:如圖7,作出點A關于l的對稱點A′,線段A′B與直線l的交點為C,點C到點A,B的距離之和最短.在直線l上另外任取一點C′,連接AC′,BC′,根據兩點間直線距離最短,可知AC+CB 案例5如果在A,B兩個城鎮之間規劃一個生態保護區,燃氣管道不能穿過該區域,要使鋪設管道的路線最短,請分別給出下列兩種情形下鋪設管道的方案(不需說明理由). ①生態保護區是正方形區域,位置如圖8所示; ②生態保護區是圓形區城,位置如圖9所示. 圖8 圖9 創設目的:首先,通過軸對稱的性質解決線段和最短的問題,幫助學生構建數學原理的邏輯思維能力,然后,用鋪設管道的方案設計拓展學生的創新思維.從圖6中簡單的兩點和一條直線,到圖8中的正方形,再到圖9中的圓,讓學生在探究中感受簡單自然美的藝術,也讓人聯想到“沒有規矩不成方圓”的哲學道理.因此,從創設例題的角度看,沒有精心的設計,就沒有問題的引領.初中生的思維發展水平還處于簡單推理階段,只有適當地對知識進行拓展、延伸,才能預防他們對問題的顧此失彼. 初中數學知識不是純粹的理論知識,它涵蓋了許多應用知識.在蘇教版七到九年級教材中的每一章最后都有“數學活動”板塊,其主要內容就是相應專題的知識應用.如,七年級上冊第一章的“數學活動”是計算“24”,這也充分說明了應用性在初中數學教學中的引領作用.正如案例3創設的問題情境,在軸對稱圖形的學習中也可用類似的例題引領學生,采用由一般到特殊的方法,讓數學概念的內涵在探究過程中生成知識體系和數學思想方法. 總之,在初中數學課堂教學中,精心創設經典例題,是幫助學生拓展知識、構建遷移思維的最佳途徑.因為,創設具有層次性的例題,可以讓學生的思維隨知識由淺入深進行拓展;創設具有多種解題方法的例題,可以讓學生的思維隨知識相互滲透進行拓展;創設具有延伸性的例題,可以讓學生的思維隨知識歸納建模進行拓展;創設具有應用性的例題,可以讓學生的思維隨知識抽象深化進行拓展.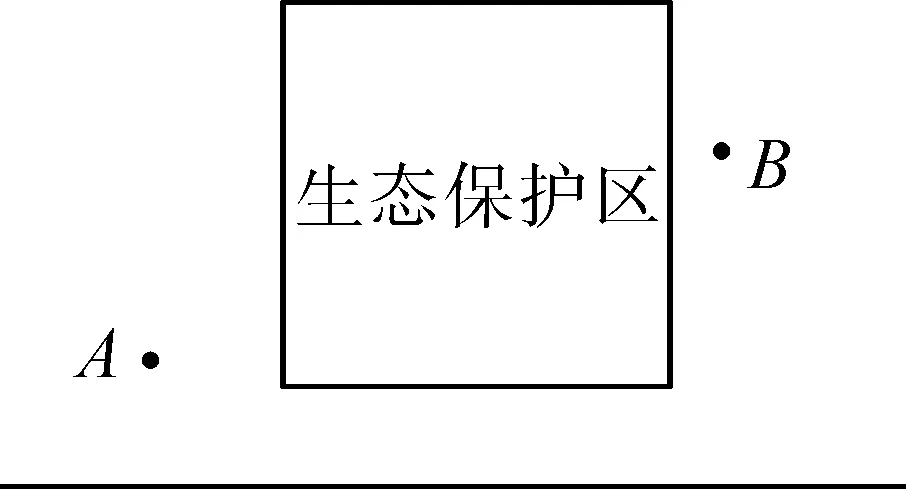

5 創設具有應用性的例題,讓學生的思維隨知識抽象深化進行拓展
6 結束語

