例析圓的切割線定理的靈活運用

?甘肅省天水市清水縣王河鎮中學 張會軍

1 定理及推論

圓的切割線定理：從圓外一點引圓的切線和割線，切線長是這點到割線與圓交點的兩條線段長的比例中項.

推論：從圓外一點引圓的兩條割線，這一點到每條割線與圓的交點的兩條線段長的積相等.

圓的切割線定理及其推論是九年級下冊數學(華東師大版)第27章第2節“與圓有關的位置關系”中的一個重要定理.在證明、計算角相等，線段相等，線段成比例等具體問題中，如果能夠靈活運用圓的切割線定理及其推論，不僅能拓寬解題思路，而且能夠收到化難為易、化繁為簡的效果[1].

2 定理及推論的靈活運用

例1已知：在△ABC中，AB=AC，以AB為直徑作半圓交BC于點D，交AC于點F，半圓圓心為點O，過點D作⊙O的切線交AC于E.

(1)求證：DE⊥AC.

(2)若AB∶BC=5∶6，AF=7，求CE的長.

分析：(1)有三種思路.證法一，首先由DE是⊙O的切線，可推證出OD⊥DE，再由△ABC是等腰三角形可推出∠C=∠ABC，∠ODB=∠C，進而可證明OD∥AC，DE⊥AC.證法二，由AB是直徑可得∠ADC=90°，只需要證∠CAD+∠EDA=90°，或∠C+∠CDE=90°，即可證得DE⊥AC.證法三，可考慮運用AB是直徑及DE為⊙O的切線這兩個條件來證明，先由已知條件推證出OD是△ABC的中位線，再根據DE是⊙O的切線即可證得DE⊥AC.

(2)有兩種思路.解法一，只需作出虛線BF即可打開思路，先利用切割線定理的推論求出CF的長度，再根據OD是△ABC的中位線就可求出CE的長度.解法二，先利用切割線定理的推論求得AC，CD的長，再結合已知條件解Rt△CDE，再通過列方程即可求出CE的長.

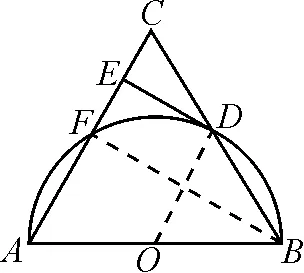
圖1

解析：(1)證法一.如圖1，連結OD.

∵DE切⊙O于點D，

∴OD⊥DE于點D.

∵OD=OB(半徑相等)，

∴∠ODB=∠ABC(等腰三角形底角相等).

∵AB=AC，

∴∠C=∠ABC.

∴∠ODB=∠C(等量代換).

∴OD∥AC(同位角相等).

∴DE⊥AC.

點評：靈活運用切線和等腰三角形的性質證明.

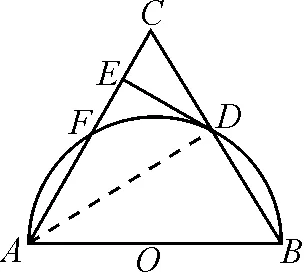
圖2

證法二:如圖2，連結AD.

∵ED切⊙O于點D，

∴ ∠EDA=∠B.

∵AB為⊙O的直徑，

∴ ∠ADB=90°.

即AD⊥BC.

∴∠DAB+∠B=90°.

∵AB=AC，AD⊥BC，

∴ ∠CAD=∠DAB，CD=BD.

∴ ∠CAD+∠EDA=∠DAB+∠B=90°.

∴DE⊥AC.

或∵ED切⊙O于點D，

∴∠EDA=∠B.

∵AB為⊙O的直徑，

∴∠ADB=90°.

∴∠ADE+∠CDE=90°.

∵AB=AC，∠C=∠B，

∴ ∠EDA=∠C.

∴∠C+∠CDE=90°.

∴DE⊥AC.

點評：在利用DE是⊙O的切線的同時，還利用了弦切角定理.

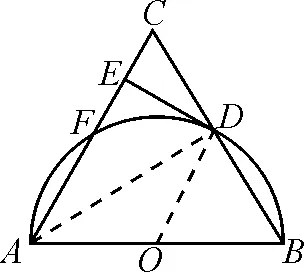
圖3

證法三:如圖3，連結OD，AD.

∵AB為⊙O的直徑，

∴AD⊥BC于點D.

又∵AB=AC，

∴CD=BD.

又∵OA=OB，

∴OD為△ABC的中位線.

∴OD∥AC.

∵DE切⊙O于D，

∴OD⊥DE.∴DE⊥AC.

點評：推證出OD是△ABC的中位線是關鍵的一步.

(2)解法一：如圖1，連結BF.由AB為⊙O的直徑，

得∠AFB=90°，即BF⊥AC于點F.

又∵DE⊥AC，

∴DE∥BF(同位角相等).

∵OD∥AC，且OA=OB，

又∵DE∥BF，

∵AB∶BC=5∶6，AF=7，

設1份為k，AB=AC=5k，BC=6k.

又CF·CA=CD·CB,

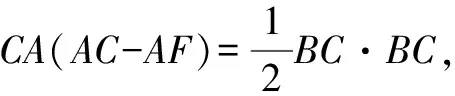
∴k1=0(舍去)，k2=5.

∴CF=AC-AF=25-7=18.

解法二：∵AB∶BC=5∶6，

設1份為k，AB=AC=5k,BC=6k,

∴CD=BD=3k，AD=4k.

∵DE⊥AC于點E，AD⊥BC于點D，

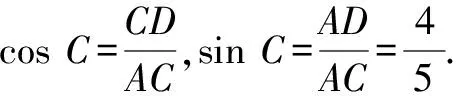
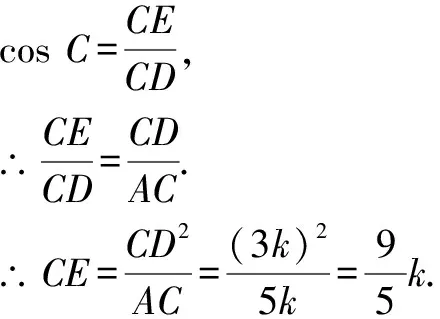
∵CF·AC=CD·BC,

又CF=AC-AF,AF=7,

∴(AC-AF)·AC=CD·BC.

(5k-7)·5k=3k·6k

∴k1=0(舍去)，k2=5.

或∵ED切⊙O于點D，

∴DE2=EF·EA=(AE-AF)·EA.

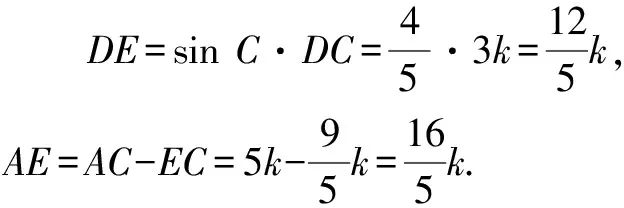
∴k1=5，k2=0(舍去).

點評：根據“點C在⊙O外，直線CFA與直線CDB為⊙O的兩條割線”的已知條件，可利用切割線定理的推論求得CF的長度，進而求出CE的長度.本題運用了數形結合的思想與方法，靈活運用了切割線定理，達到了一題多證、一題多解、左右逢源的效果.

例2已知PT切⊙O于點T，割線PAB交⊙O于點A，B，且AB過O點，∠OPT=30°，PT=20 cm，求PB的長.

分析：按照“執果索因”的解題思路，要想求PB的長，需先求出PA的長.因為∠OPT=30°是一個特殊角，所以可考慮構造一個直角三角形，連接OT，得到Rt△OPT，則可得出OP=2OT=2r，AP=r，PB=3r，即可由切割線定理求出r，進而求出PB的長.

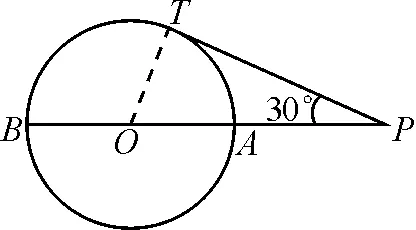
圖4

解析：如圖4， 連接OT，設⊙O的半徑為r.因為PT切⊙O于點T，所以OT⊥PT.因為∠OPT=30°，所以OP=2OT=2r，于是PB=3r，PA=r.

由PT2=PA·PB(切割線定理)，PT=20，

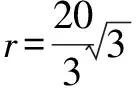
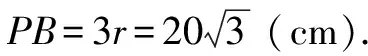
點評：本題由已知“P為⊙O外一點，PT為切線”，可直接應用切割線定理PT2=PA·PB來求解.

3 結論

圓的切割線定理及其推論是初中平面幾何中的重要內容，許多與圓有關的問題，我們都可以直接應用它或借助它的轉化獲得解決[2].從上述例題的解題思路與方法中我們可以看到，所謂的“靈活運用”，主要是指設法把不能直接運用切割線定理解決的問題轉化為能夠運用定理來解決的問題.解題思路往往表現為幾種方法的綜合運用，例如運用數形結合法，利用三角形、線段與比例的性質，結合三角函數轉化為方程求解，等等.總之，“運用之妙存乎一心”，只有認真分析題目的已知條件，找到問題的內在聯系，靈活變通，才能找到解題的突破口.