Probabilistic quantum teleportation of shared quantum secret
Hengji Li(李恒吉) Jian Li(李劍) and Xiubo Chen(陳秀波)
1School of Artificial Intelligence,Beijing University of Posts and Telecommunications,Beijing 100876,China
2School of Cyberspace Security,Beijing University of Posts and Telecommunications,Beijing 100876,China
3The Laboratory of Cryptography of Zhejiang Province,Hangzhou 311121,China
4Quantum Technology Laboratory and Applied Mechanics Group,University of Milan,Milan 20133,Italy
Keywords: probabilistic quantum teleportation,shared quantum secret,partially entangled GHZ state
1. Introduction
Quantum teleportation[1]uses a pre-shared quantum channel to faithfully transfer an unknown quantum state between distant nodes within a network.Nowadays,it has played a pivotal role in various quantum information technologies such as measurement-based quantum computation,[2]quantum network[3,4]and a possible further quantum Internet.[5,6]Experimentally, the teleportation of arbitrary quantum states from a two-dimensional qubit[7]to a high-dimensional qudit[8]has been realized.
To realize versatile quantum networks, the incorporation of multiple participants needs to be further considered. Controlled teleportation has been proposed which can split quantum information from one sender to multiple receivers.[9-12]Teleportations of multiparty states have also been demonstrated and studied,[13,14]in which the multipartite entanglement state could be teleported. Besides quantum teleportation, controlled remote state preparation is presented,[15,16]where the goal can only be achieved with the control of the agents. A distributed quantum computation with the control of the controller[17]is proposed. Moreover, there are other typical quantum communication protocols that could facilitate the construction of versatile quantum networks.[18-25]Various kinds of quantum cryptography protocols,such as quantum key distribution,[18,19]quantum secure direct communication[20]and quantum secret sharing,[21,22]could generate a secure communication channel. In such a way, it is impossible in principle to eavesdrop without a high probability of disturbing the transmission, which will be detected.Considering a real situation,for obtaining deterministically maximally entangled pure states,quantum entanglement concentration and purification schemes are proposed,[23-25]which are very important elements for long-distance quantum communication.
Very recently, Leeet al.proposed a teleportation protocol of shared quantum secret states among multiple senders and receivers.[4]It can teleport quantum information shared by an arbitrary number of senders to another arbitrary number of receivers, where neither any single-nor subparties of senders and receivers can fully access the secret quantum information.This indicates that we can relay quantum information over a network in an efficient and distributed manner without requiring fully trusted central or intermediate nodes.[26]In Leeet al.’s scheme,[4]a multipartite maximally entangled GHZ state andntimes of standard Bell-state measurements are required.It can perfectly achieve the teleportation with unit probability.
Due to the fragility of the entanglement[27]and the inevitable effects of environmental noise,[28,29]a maximally entangled state could be degraded into a partially entangled state. On the one hand, employing entanglement concentration,[30,31]one can probabilistically obtain a maximally entangled state,but,for this to occur,a large ensemble of partially entangled states is required. On the other hand,probabilistic teleportation was proposed via direct utilization of a partially entangled state in the network channel. In Ref.[32],the sender still makes a standard Bell-state measurement,however,on reconstruction of the original state,the receiver needs to introduce an auxiliary particle and then perform a twoparticle unitary transformation. Considering the fact that there is one to one correspondence between the joint measurement result and the final state,the proper measurement result might lead the receiver to recover the target state. For example,generalized Bell-state[33]and GHZ measurements[14]have been introduced to probabilistically transfer the state without an auxiliary particle.
In this manuscript, we consider the partially entangled GHZ state as the network channel to achieve the teleportation of shared quantum secret. It is shown that the shared quantum secret can reach its destination with unity fidelity. However,the price we pay to achieve unity fidelity is that the successful probability is less than 1. Two kinds of approaches are given,inspired by prior work.[32,33]The first one involves performingntimes of standard Bell-state measurements, however at the end of the protocol,introduction of an auxiliary qubit and adoption of a general evolution[32]is required at any receiver’s location. The second possibility involves performing a generalized Bell-state measurement[33]at only one sender’s location. Moreover, the successful probability is given, which is determined by the degree of the entanglement of the channel.
The paper is structured as follows. Firstly, the original protocols is shown in Section 2,and then we present two new proposals of probabilistic teleportation of the shared quantum secret in Section 3. In Section 4,we discuss our two schemes and Section 5 contains our conclusions.
2. The original protocol


Then they communicate the outcomes to the receiversrj.Conditioned on the results, the state of the channel at the receivers’locations is|φ〉mrplus logical Pauli operators. Lastly,the receivers can reconstruct the target state|φ〉mrby carrying out the local Pauli operators,according to the results of all the senders. Figure 1 shows the protocol, while taking|ε〉n+mas the network channel andM1=···=Mn=B.
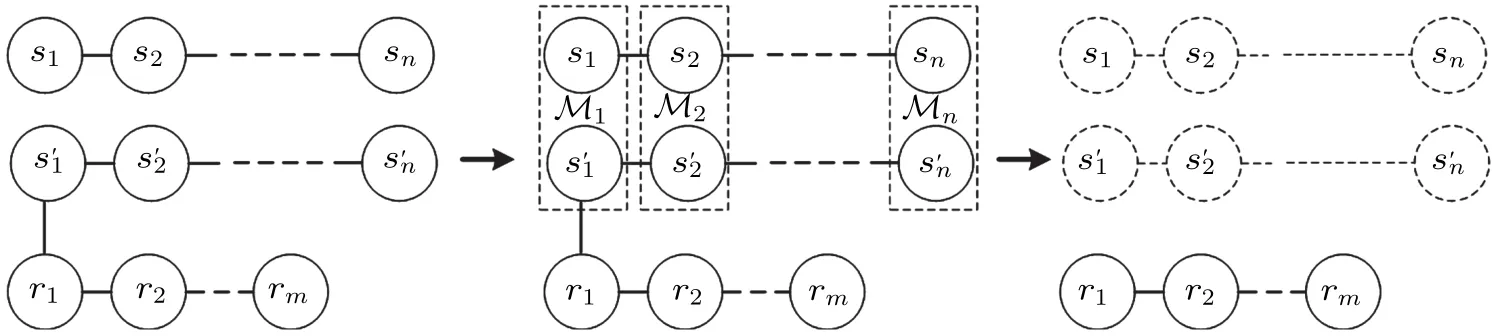
Fig. 1. The (n+m)-particle entangled state ({s'1,s'2,...,s'n} and {r1,r2,...,rm}), as the network channel is utilized to teleport a quantum secret|φ〉ns ({s1,s2,...,sn})between n senders and m receivers. After performing n joint measurements(the dotted frame),denoted as Mi,the receivers can reconstruct the shared secret.
3. Teleportation with a partial multipartite entanglement state
Instead of sharing a GHZ state, the senders and the receivers may initially share a non-maximally entangled state of the form

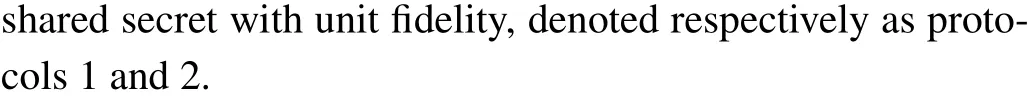
3.1. Teleportation based on n times of standard Bell state measurements
In this subsection, we present our simple scheme, wherentimes ofBs are still performed at every sender’s location.Figure 1 shows the protocol, while taking|ε'〉n+mas the network channel andM1=···=Mn=B. It is shown here that the shared quantum secret can be recovered with unit fidelity,however, a proper generalized revolution is needed. First of all,write the initial composite system as
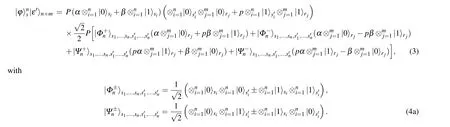

After performingntimes ofBs, they inform the receivers of the results via the classical channels. Define the measurement result of the sendersiaszixiand let the classical bits{00,10,01,11}correspond to{|φ+〉,|φ-〉,|ψ+〉,|ψ-〉}.


Next,he implements aZ-measurement on the auxiliary qubit.When the result is|0〉aux,the target state can be recovered with the probability|Pp|2. Adding up both the contributions, the optimal probability of successful teleportation is obtained asQ1=2|Pp|2.
3.2. Teleportation based on a single generalized Bell state measurement
In the subsection above, for teleporting the initial state with unity fidelity, an auxiliary qubit needs to be introduced and a two-particle collective transformation is then performed.Here, we show that it is possible for the receivers to recover the target state without the auxiliary qubit, though not with unit probability. To fulfill this, instead of performingn Bs,a single generalized Bell state measurement(BG)is required.Firstly,define the generalized Bell basis[33]


Adjust the order and rewrite the composite system as
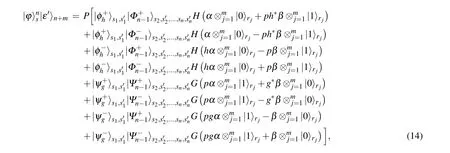


4. Analysis
The access information in the probabilistic teleportation of shared secret state can be shown by the same methods presented in Ref. [4]. Any subparties can not fully access the quantum secret during the teleportation procedures. Note thatntimes ofBs are not necessary. Actually, only one Bellstate measurement is sufficient for implementing the protocol.Rewrite Eqs.(5a)and(5b)as(without normalized)
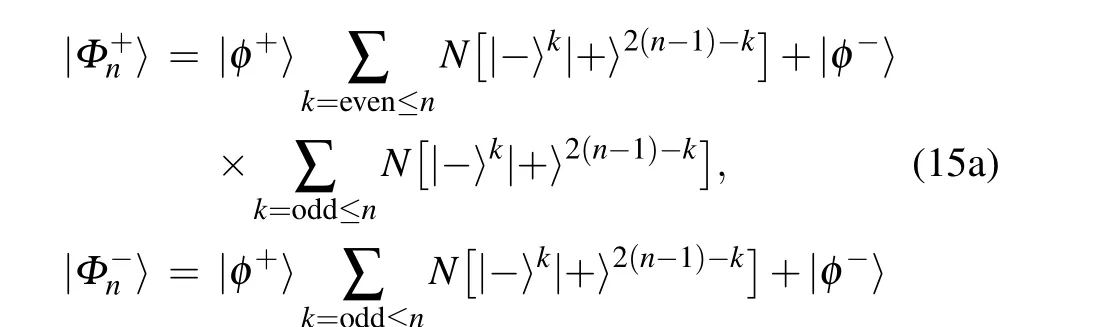


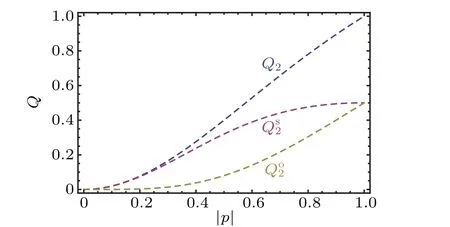
Fig.2. The successful probability Q2,Qs2 and Qo2.
In general, decoherence and noise degrade the entanglement of the channel in a rather complicated way. For example,the initial two-qubit network channel might evolve into a mixed state(Werner state),[40]which is non unitary. A quantum state can not be teleported via the channel with unit fidelity, even if the successful probability is less than unit.[41]Here, we focus on the question whether the teleportation can be achieved with unit fidelity. Therefore,we consider the case that a maximally entangled pure channel still evolves to a pure partially entangled one. Note that for some kinds of unitary noises,[42]such as bit and phase flip noise, the degree of the entanglement of the channel remains unchanged. In this case,the receivers can easily overcome it by performing the proper local Pauli operations at the end of the protocol. For example,while a phase flip noise occurs at any sender’s location in the network channel,any receiver could carry out an extraσzgate to retrieve the teleported state.
5. Conclusion
In summary, in this work, we describe two optimal methods for teleporting a shared quantum secret via a nonmaximally multipartite GHZ state in a quantum network. The unit fidelity transfer of the initial state can be achieved with a calculable probability, which is determined by the degree of entanglement of the channel. For reconstructing the state,an auxiliary qubit is required to be introduced at anyone of the receivers in the first strategy. However, in the second approach, after any sender performs the generalized Bell-state measurement,the state can be recovered with a certain probability without the need for an auxiliary qubit. We will discuss the case that the network channel degrades in a rather complicated way in our future work.
Acknowledgements
Project supported by the Open Fund of Advanced Cryptography and System Security Key Laboratory of Sichuan Province, China (Grant No. SKLACSS-202108), the Open Research Fund of Key Laboratory of Cryptography of Zhejiang Province, China (Grant No. ZCL21006), the National Natural Science Foundation of China(Grant Nos.U1636106,92046001, 61671087, 61962009, and 61170272), the BUPT Excellent Ph.D.Students Foundation(Grant No.CX2020310),Natural Science Foundation of Beijing Municipality, China(Grant No. 4182006), and the Fundamental Research Funds for the Central Universities,China(Grant No.2019XD-A02).
- Chinese Physics B的其它文章
- Erratum to“Accurate determination of film thickness by low-angle x-ray reflection”
- Anionic redox reaction mechanism in Na-ion batteries
- X-ray phase-sensitive microscope imaging with a grating interferometer: Theory and simulation
- Regulation of the intermittent release of giant unilamellar vesicles under osmotic pressure
- Bioinspired tactile perception platform with information encryption function
- Quantum oscillations in a hexagonal boron nitride-supported single crystalline InSb nanosheet

