Definition and expression of non-symmetric physical properties in space for uniaxial crystals
Xiaojie Guo(郭曉杰) Lijuan Chen(陳麗娟) Zeliang Gao(高澤亮) Xin Yin(尹鑫) and Xutang Tao(陶緒堂)
1State Key Laboratory of Crystal Materials,Shandong University,Jinan 250100,China
2School of Physics Science,University of Jinan,Jinan 250100,China
Keywords: uniaxial crystals, effective physical constant space distributions, the positive direction of optical coordinate axis
1. Introduction
With the rapid development of modern science and technology, crystals play an irreplaceable role in electrical and optical applications. The research on crystals is mainly focused on crystal growth techniques,systematic measurements of physical properties and fabrication of devices. Detailed research into crystal physical properties is a precondition of crystal applications. Meanwhile,the fabrication of crystal devices is also based on crystal physical properties. For crystallographers, crystal anisotropic properties are usually described by tensors. And the tensors are given in matrix form through symmetry operations in the crystallographic coordinate system.[1-4]However, for physicists, crystal physical properties are usually expressed in the physical coordinate system,which is not always the same as the crystallographic coordinate system. The space is divided into eight imaginary quadrants in the physical coordinate system. The tensor forms describing crystal physical properties are only given in quadrant I.In the research and applications of crystal physical properties, the physical constants and effective physical constants will be obtained and calculated by rotating crystal samples in the physical coordinate system.[5]The relative signs of the tensor elements indicate the anisotropic physical properties defined by the coordinate axes directions. The spatial distributions of effective physical constants for biaxial crystals have been analyzed.[6]The results show that crystal physical properties of a monoclinic system are not the same in adjacent quadrants,which is caused by the sign changes of tensor elements.[6]The different distributions of physical properties in different quadrants will bring ambiguities and difficulties to the research and applications of crystal physical properties.Uniaxial crystals have more and higher symmetrical components than biaxial crystals, but some special point groups in uniaxial crystals only have a symmetrical component along one coordinate axis. Hence, there are also similar ambiguities and difficulties for uniaxial crystals. The relative signs of the tensor elements and spatial symmetry of effective physical properties in uniaxial crystals have attracted our attention.
In this paper, the signs of tensor elements for uniaxial crystals in space are investigated using the subscript change method. The spatial distributions of efficient physical constants describing second-order, third-order, and fourth-order tensors are discussed in detail. Our results show that the physical properties of special point groups in uniaxial crystals also have non-symmetry, which is similar to that of biaxial crystals.[6]The difference between crystallographic and physical coordinate systems and the lack of crystal symmetry operations lead to the non-symmetry of crystal physical properties. To avoid ambiguities and difficulties in the research and applications of crystals,we proposed to utilize piezoelectric properties to define the positive direction of the optical coordinate axis prior to the research and applications of optical properties.
2. Subscripts of tensor elements in the rectangular coordinate system
As is well known,anisotropic physical properties are described by tensors,including thermal,electro-optic,nonlinear optical, dielectric, piezoelectric properties, and so on. The physical coordinate system is defined in a rectangular coordinate system, but it is not exactly the same as the crystallographic coordinate system in some special point groups.[7]As shown in Fig.1,the rectangular coordinate system divides the space into eight quadrants, and the positive directions of the coordinate axes are defined. The relationship between the subscripts of tensor elements and coordinate axes can be represented as 1→x,-1→-x, 2→y,-2→-y, 3→z, and-3→-z. The signs of different subscripts in eight quadrants are listed in Table 1. Due to the diversity of physical properties, uniaxial crystals with asymmetrical structures are discussed in detail.
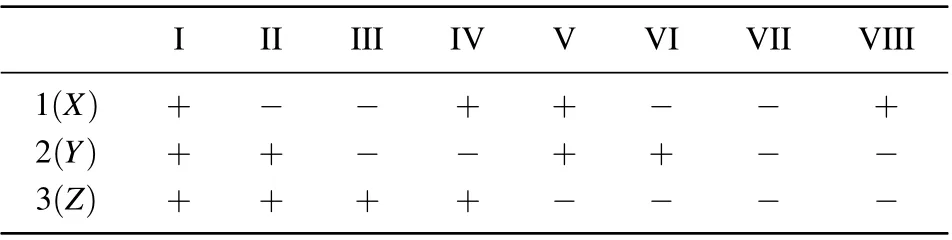
Table 1. The signs of coordinate axes in each quadrant.

Fig.1. The positive direction definitions of eight quadrants.
2.1. The sign changes of second-order tensor matrix elements
Taking the dielectric property as an example, the sign changes of the second-order tensor element subscripts are analyzed. Cubic crystals exhibit isotropic dielectric properties.In addition,crystals in trigonal,tetragonal,and hexagonal systems have only two principal axial coefficients.[8]Obviously,the subscripts of the dielectric constant are equivalent(i=j),which means that the positive direction has no direct effect on the signs of tensor elements,as shown below:
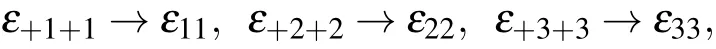

There is only one matrix form
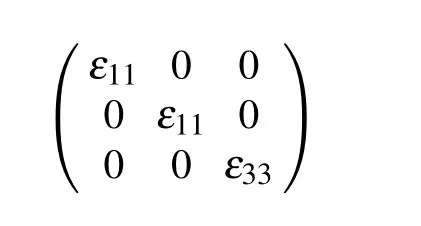
in each quadrant. The analysis of dielectric properties is also applicable to other physical properties represented by secondorder tensors in uniaxial crystals,including electrical conductivity(μij), resistivity(ρi j), dielectric isolation rate(βij), dielectric polarizability(χij),magnetic permeability(μi j),thermal expansion(αij),and thermal conductivity(κij).
2.2. The sign changes of the third-order tensor matrix elements
Crystals in noncentrosymmetric point groups possess physical properties that are described by third-order tensors. These physical properties include piezoelectric,electricoptical, and second-order nonlinear optical properties. The third-order tensors contain simplified subscripts and more tensor elements than second-order tensors. Therefore,the piezoelectric matrixdijis also taken as an example to analyze the element sign changes of uniaxial crystals. The simplified subscriptjis an abbreviation of two subscriptslandk,expressed as 1→1,1;2→2,2;3→3,3;4→2,3;5→1,3;and 6→1,2. Due to the different directions of the coordinate axes, the subscript signs will change in each quadrant. The signs of the piezoelectric matrix elements are listed in Table 2.
In practical crystal applications,only the absolute values or the square of the extremum of efficient physical constants are considered. Therefore, the negative sign in front of the matrix can be ignored. As shown in Table 2,the matrix forms in eight quadrants are the same in the point groups 422,4mm,ˉ42m, 622, 6mm, ˉ6m2 and the cubic system, which are similar to those of an orthogonal system.[6]There are two matrix forms in point groups 32,3m,4, ˉ4,6,and ˉ6,respectively,which are similar to those of a monoclinic system.[6]Point group 3 has four matrix forms in space, which is similar to a triclinic system.[6]
Our analysis indicates that although uniaxial crystals have higher symmetry than biaxial crystals,the piezoelectric properties in specific point groups also exhibit similar tensor form changes to biaxial crystals. The tensor form changes of piezoelectric properties can be extended to other physical properties that are described by third-order tensors.

Table 2. The piezoelectric matrix elements of uniaxial crystals.

Table 2. Continued.

Table 2. Continued.
2.3. The sign changes of fourth-order tensor matrix elements
The second-order electric-optical, elastic, elastic rigidity,and elastic-optical properties are described by fourth-order tensors. The two subscripts of the fourth-order tensors are simplified, which is as the same as that of subscriptjin the piezoelectric tensors. Using similar analysis to that used for third-order tensors, the tensor forms of elastic constants (sij)are listed in Table 3.
Obviously,there is only one tensor form in the hexagonal system, cubic system, and point groups 4mm, ˉ42m, 422, and 4/mmm. There are four tensor forms in point groups 3 andˉ3. In tetragonal and trigonal systems, the matrixes have two forms in point groups 32,3m, ˉ3m,4, ˉ4 and 4/m. The analysis of elastic constants is applicable for all physical properties that are described by fourth-order tensors.
3. The distributions and discussions of the efficient physical properties
The dielectric properties only have axial elements, and the distribution of the dielectric properties in uniaxial crystals can be expressed as an ellipsoid with long and short axes that are parallel to the coordinate axes. This means that the distribution of the dielectric properties is the same in each quadrant.
In our research, the distributions of piezoelectric properties in point groups 3mand 4 are taken as examples. The values of the piezoelectric constantsd'23andd'21in point groups 3mand 4 can be expressed as follows using the coordinate transformation method[9-13]in quadrants I and IV:
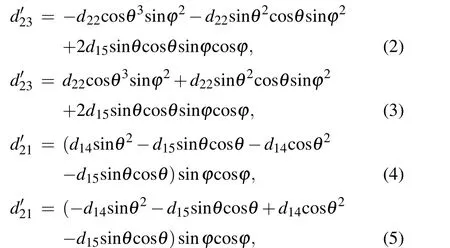
in whichθandφ(0<θ <90°, 0<φ <90°) are the rotation angles around the piezoelectric axesZandY, respectively. Due to the sign changes of the matrix elementsd22andd14,the distributions of the piezoelectric constants in quadrant I are different from those in quadrant IV.The distributions ofd'23andd'21in other quadrants can be obtained using the same coordinate transformation method. It is worth noting that only piezoelectric properties containing sign changes exhibit spatial non-symmetry in adjacent quadrants. The results are also suitable for other physical properties that are described by thirdorder and fourth-order tensors in uniaxial crystals.

Table 3. The elastic matrix elements of uniaxial crystals.

Table 3. Continued.
The crystal physical coordinate system is used to describe anisotropic physical properties. However, the symmetry of crystals in crystallography is obtained based on the rotation operation of the crystallographic coordinate system.The traditional crystallographic coordinate system only provides a definition of the lattice parameters and the angles, and does not give the positive and negative directions of thea,b,andccoordinate axes. But the physical properties have positive and negative effects,such as the piezoelectric constantd33: the value is equal but the sign is opposite in the opposite direction. In addition, when studying the physical properties and devices of crystals,the crystal samples are manufactured in the physical coordinate system (rectangular coordinate system). For some specific point groups, because the crystallographic coordinate system is a non-rectangular coordinate system, the physical coordinate system is not consistent with the crystallographic coordinate system. Taking point group 3 as an example,the relationship between the angles of crystallographic coordinate axes is as follows:α=β=90°,γ=120°. The relationship between the angles of physical coordinate axes isα=β=γ=90°.According to the piezoelectric rule of IEEE,Z//c,X//a, exist andYis determined by the right-hand rule in a trigonal system. As shown in Fig.2,the physical properties along the crystallographic coordinateaandbaxes are the same,but the physical properties of the violet line and red line directions that are symmetrically distributed along the physical coordinateYaxis are not the same. Hence,we believe that the difference between the crystallography and physical coordinate systems is the source of the non-symmetry in physical properties.

Fig.2. The crystallographic coordinate system and physical coordinate system of point group 3.
Meanwhile,the lack of crystal symmetry operation in different directions also contributes to non-symmetry of physical properties in uniaxial crystals. Taking point group 4 as an example, the crystallographic and physical coordinate systems are shown in Fig.3. In the crystallographic coordinate system,there is only a quartic axis along thecaxis. Hence,the physical properties along the violet line directions are the same.However,due to the lack of a symmetry plane along theaaxis,the physical properties along the blue dotted line are not the same as in the violet line direction.Therefore,the lack of crystal symmetry operations is also considered to be one origin of the non-symmetry. The piezoelectric coordinate system is defined according to the IEEE standard.[14]We take the direction of thed33positive value as the positive direction of theZaxis,and other positive directions obey the right-hand rule. The piezoelectric properties along the violet and blue lines can be distinguished byθand-θ. In the optical coordinate system,the directions of the coordinate axes only obey the right-hand rule.Due to no positive direction definition of theZaxis,there are two optical coordinate definitions, as shown in Fig. 3. In optical properties research and applications, crystal samples are manufactured in the crystallographic or physical coordinate systems. Ifθis the angle of the sample from theXaxis to the light propagation direction, there are two directions with different optical properties,and they cannot be distinguished.According to the tensor analysis, all the optical properties of crystals with different tensor forms show the same difficulties as the crystals of point group 4.
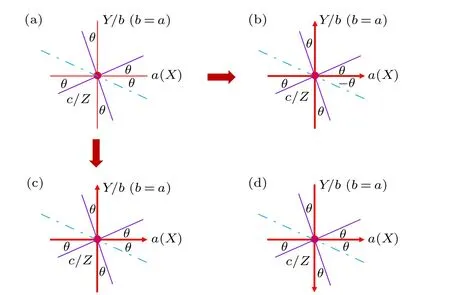
Fig.3. The optical coordinate definitions of point group 4 based on crystallographic and physical coordinate systems.
To accurately describe and apply the physical properties,the cutting directions of crystals should be in the assigned quadrant. This means that the positive direction of the optical coordinate axis should be defined. As shown in Tables 2 and 3, crystals with both piezoelectric and optical properties are described by third-order and fourth-order tensors. The positive direction of the optical coordinate axis cannot be defined by optical properties,but it can be determined with the aid of the piezoelectric properties. The positive directions of the optical axis do not need to be specified in the point groups 622,422,23, ˉ6m2, ˉ42m,andˉ43m.There are piezoelectric constantsdii(i=1, 2, or 3) in the point groups 32, 3m, 4, 6, ˉ6, and 3,respectively. Hence,the positive direction of the optical coordinate axis can be defined withdiiexhibiting positive values,as shown in Fig. 4. For point groups 3 and 3min the trigonal system,the direction of the piezoelectric constantd33→+is the positive direction ofnc, and the direction ofd22→+is the positive direction ofnacin point group 3m. For point group 32, the direction ofd11→+ is the positive direction ofna. For point groups 4mmand 4 in the tetragonal system,the direction ofd33→+ is the positive direction ofnc. For point group ˉ4, the direction ofd31→+ is the positive directionnc. For point groups 6 and 6mmin the hexagonal system,the direction ofd33→+is the positive directionnc. The coordinate axes, which have not been defined above, should obey the right-hand rule.
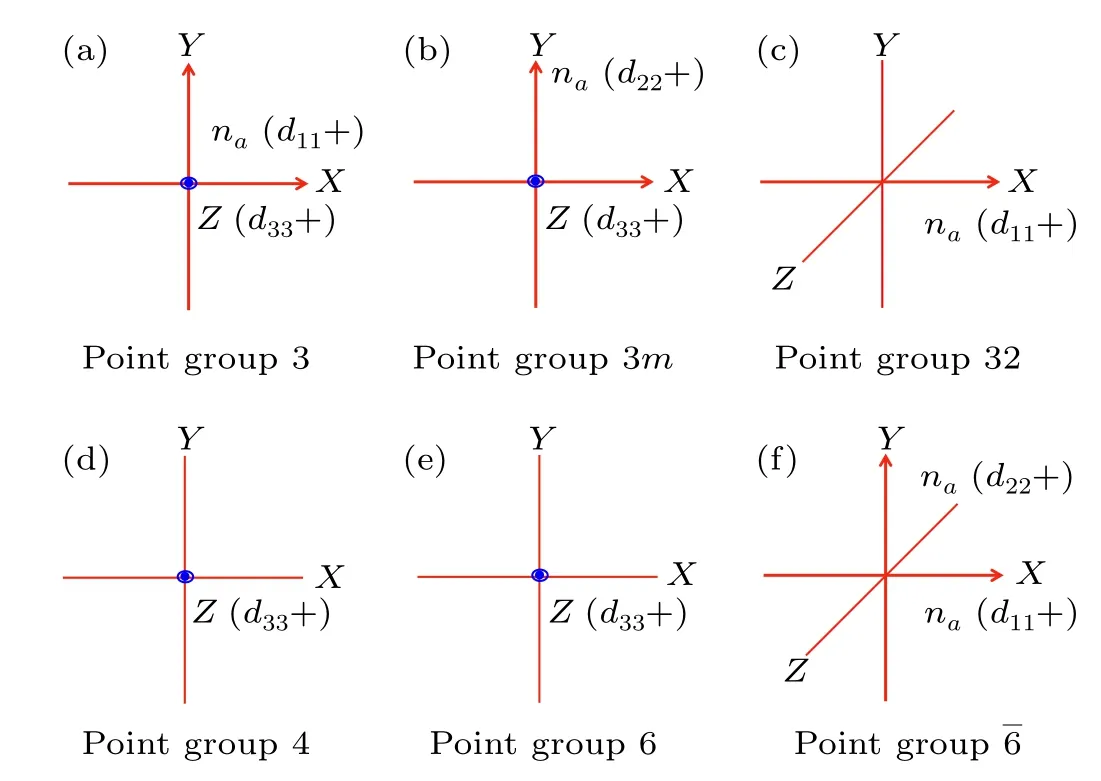
Fig.4. Positive direction definitions of the optical coordinate axis in different point groups: (a) point group 3; (b) point group 3m; (c) point group 32; (d)point group 4;(e)point group 6;(f)point group ˉ6.
4. Conclusion and perspectives
In conclusion,the sign changes of physical properties described by second-order,third-order,and fourth-order tensors of uniaxial crystals are given in space. The physical constant distributions of special point groups in uniaxial crystals show non-symmetry in adjacent quadrants. The difference between the crystallographic and physical coordinate systems and the lack of crystal symmetry operations are considered to be the origins of the non-symmetry.The lack of the positive direction of the optical coordinate axis makes research and application of optical characteristics ambiguous and difficult. Therefore,we proposed the use of piezoelectric properties to define the positive directions of the optical coordinate axis prior to the research and applications of optical properties.
Acknowledgments
Project supported by the National Natural Science Foundation of China (Grant Nos. 51772170, 51572155, and 11504389),the National Key Research and Development Program of China(Grant No.2016YFB1102201),and the Young Scholars Program(Grant No.2018WLJH67).
- Chinese Physics B的其它文章
- Erratum to“Accurate determination of film thickness by low-angle x-ray reflection”
- Anionic redox reaction mechanism in Na-ion batteries
- X-ray phase-sensitive microscope imaging with a grating interferometer: Theory and simulation
- Regulation of the intermittent release of giant unilamellar vesicles under osmotic pressure
- Bioinspired tactile perception platform with information encryption function
- Quantum oscillations in a hexagonal boron nitride-supported single crystalline InSb nanosheet

