基于加權L1 范數最小化算法的地震數據重建方法研究
梁 爽,武召祺,彭 清
(東華理工大學,江西 南昌 330013)
引言
自工業革命開始,化石能源日益成為社會經濟發展的動力源泉,并為人類的生存和發展提供了堅實的物質基礎,同時經濟發展也會進一步促進能源的勘探、開采和利用,可見社會經濟發展和化石能源之間有著密切關聯。目前,我國經濟正處于快速發展階段,對煤、石油、天然氣等資源需求量不斷增大,資源勘探也就成了經濟發展的重中之重[1]。地震勘探可以利用人工激發的地震波獲取地下礦藏信息,是一種高效的油氣勘探方法,在資源勘探當中被廣泛應用,為我國煤炭、石油等行業發展做出了巨大貢獻。
基于大部分信號具有稀疏性的特點,2004 年Donoho 提出壓縮感知理論將地震數據重建問題轉化為簡單的去噪問題,實現利用較少采集數據獲得近似完整的地震勘探效果[2]。該理論具有采樣速度快、存儲空間小、經濟成本低的優點[3]。重建算法是壓縮感知理論的核心問題,通常將壓縮感知理論重建算法分為3大類:第一類為貪婪算法,包括匹配追蹤算法、正交匹配追蹤算法等;第二類為組合算法,包括傅立葉采樣、鏈式追蹤及HHS 追蹤等;第三類為凸優化算法,包括域值迭代法、投影梯度算法等[4-5]。L1 范數譜投影梯度算法具有操作簡單、適用處理海量數據的特點。但該方法在數據重建過程中相鄰切片是獨立重建的,忽略了地震數據有效波具有連續性的特點,為此本研究提出一種基于加權L1 范數最小化算法的地震數據重建方法,該方法以壓縮感知理論為基礎,以曲波變換為稀疏基,用不同時間切片有效波曲波系數的相關性作為先驗信息,從而提出加權L1 范數約束條件,選取相鄰切片的有效數據進行重建,使重建后的地震數據同相軸更為連續,在實現高精度地震數據重建同時也進一步提升抗噪能力。將本研究方法應用于處理實際野外采集數據,實驗結果驗證了本研究提出方法的實用性與有效性。
1 數據重建原理
1.1 壓縮感知理論
壓縮感知原理充分利用信號具有稀疏性的特點,解決了尼奎斯特理論采樣頻率必須大于信號最高頻率2 倍的要求,僅用少量數據就可以恢復出近似完整原始數據f?RN。

式中,ψ 為隨機采樣矩陣,y?R M(M?N)為缺失數據,因此在 ψ和y 已知的前提條件下,可以通過地震數據重建恢復出近似完整的地震數據f。由于地震數據在時間域內不具有稀疏性,本研究以曲波變換φ為稀疏基,使f 在變換域 φ內進行稀疏表示,則

式中,α 為稀疏系數,H 為共軛轉置矩陣,則公式(1)可寫為

當 ψ滿足限制等距特性時,可以通過L1 范數最小化算法不斷促進求解最優稀疏系數,即
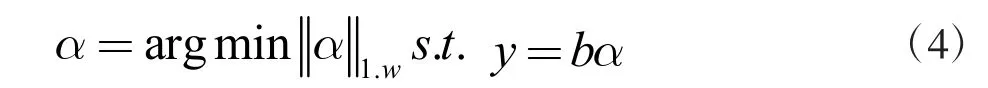
1.2 加權L1 范數最小化算法
地震數據的物理屬性具有連續性,因此可以對地震數據進行加窗處理,把地震數據轉化成時間切片,利用相鄰切片之間的高度相關性促進稀疏系數α 的恢復,但標準L1 范數最小化方法并沒有考慮到這種情況,因此本研究用加權L1 范數最小化算法代替標準L1 范數最小化,將公式(4)改為:


經過實測分析,當γ=0.3 時加權L1 范數最小化算法重建后信噪比值最大,重建效果最佳,因此在后續實驗當中參數γ 均取值為0.3。
2 實測數據處理

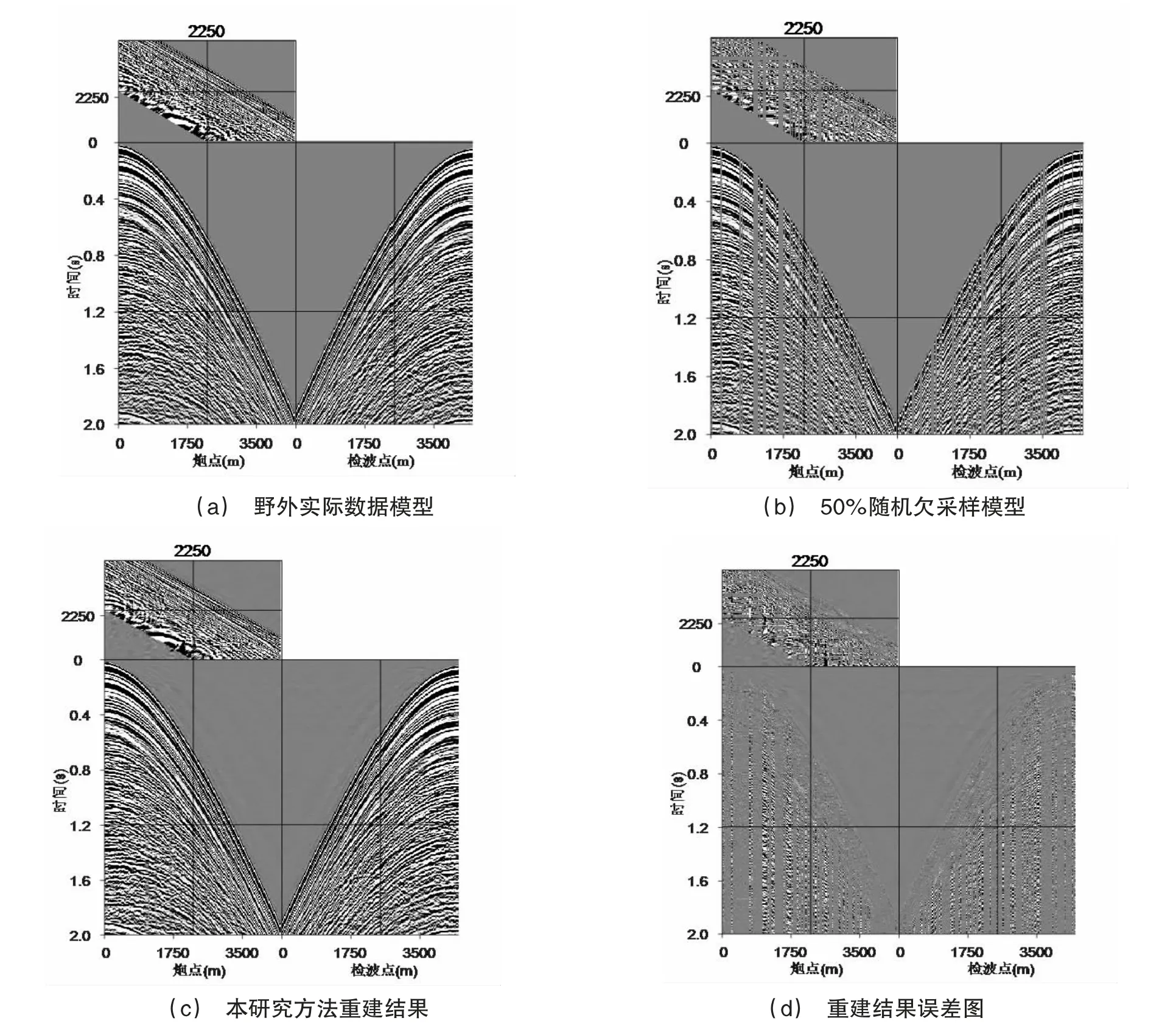
圖1 野外地震數據模型及重建結果
為進一步驗證文本方法兼具實用性與有效性,還采用標準L1 范數最小化算法對50%隨機缺失數據進行重建,兩種算法在不同迭代次數下的信噪比關系圖見圖2,由圖2 可知,起初隨著迭代次數增加,兩種算法重建后信噪比均有效增長,但當迭代次數超出某一數值后,信噪比數值將趨于穩定,此時加權L1 范數最小化算法的重建結果要明顯優于標準L1 范數最小化算法。綜上所述可以得出,在處理野外實際數據中,本研究方法可以實現高精度的地震數據重建。

圖2 不同迭代次數與信噪比關系曲線圖
3 結論
(1) 為了提高地震數據重建精度,本研究在標準L1 范數最小化算法的基礎上,依據地震數據有效波具有連續性的特點,提出加權L1 范數最小化重建算法。對比這兩種算法可以得出,本研究方法重建后信噪比數值更大,重建效果更佳。
(2) 實驗結果表明,對于處理野外采集的缺失地震數據,本研究方法具有重建誤差小,魯棒性好和抗噪能力強的優點。因此資金成本,重建精度這兩方面方面考慮,本研究所提出的方法具有可行性和實用性。

