動態機車工況下質子交換膜燃料電池電堆衰退性能分析

張雪霞 黃 平 蔣 宇 陳維榮

動態機車工況下質子交換膜燃料電池電堆衰退性能分析

張雪霞 黃 平 蔣 宇 陳維榮

（西南交通大學電氣工程學院 成都 611756）

為探究質子交換膜燃料電池（PEMFC）電堆在動態機車工況下的衰退性能，該文結合極化曲線、等效電路模型（ECM）方法和弛豫時間分布（DRT）方法對電池進行分析。針對5kW電堆，測量了機車工況下運行0h、110h、220h及330h后，第1、20和40片電池的極化曲線和電化學阻抗譜（EIS）。建立PEMFC三階等效電路模型，根據模型參數分析PEMFC內部變化。計算EIS相應的DRT，根據不同波峰解釋PEMFC各極化過程的變化。結果表明：該電堆不同單片的主要損耗都發生在氧氣還原反應過程和質量傳輸過程中，但動態工況下不同單片的衰退趨勢不一致。電堆入口的電池1在110～220h期間衰退速率最快，電堆中間的電池20衰退速率隨時間逐漸加快，電堆出口電池40在220～330h期間衰退速率最快。且由于電池40在0h未活化完全，導致其在0～110h期間出現性能提升。

動態機車工況 質子交換膜燃料電池 電堆衰退 電化學阻抗譜 不一致性

0 引言

隨著我國鐵路技術的快速發展，電氣化率逐年增長。然而，環境污染和能源危機成為我國鐵路發展的一大挑戰，亟需尋找可替代的清潔能源[1]。質子交換膜燃料電池（Proton Exchange Membrane Fuel Cell, PEMFC）是一種將氫能轉化為電能的一種裝置，其具有高效率、低排放和啟動快等特性，已得到廣泛的應用。與傳統機車（內燃機車和電力機車）相比，以PEMFC為動力的機車不僅無需傳統的牽引供電系統，也可以解決軌道交通所產生的污染和能源問題[2-3]。然而，PEMFC的耐久性仍制約著其在軌道交通領域的大規模應用[4-6]。

PEMFC在不同工況（穩態工況或動態工況）下的壽命通常不同。運行在恒電流的穩態工況下，電池壽命最高能達到5 000h以上，而動態工況下的壽命將大幅度縮短[7]。對于機車應用，PEMFC主要運行在動態循環工況下。動態工況包含啟停、怠速、加減載等階段。動態工況下快速變化的負載，及易出現的欠氣和局部熱點等故障都會加速PEMFC的衰退[8]。同時，電堆不同位置處電池的性能不一致性也會對PEMFC的壽命產生影響。因此，分析動態機車工況下PEMFC電堆的衰退性能具有必要性[9-10]。

目前，表征PEMFC的性能可通過透射電子顯微鏡、掃描電子顯微鏡、X射線衍射、循環伏安法、極化曲線及電化學阻抗譜（Electrochemical Impedance Spectroscopy, EIS）等[11-15]。其中，EIS方法有助于分析PEMFC的內部變化及發生的極化過程。為關聯EIS與PEMFC各部件的狀態，通常建立等效電路模型（Equivalent Circuit Model, ECM）來擬合EIS數據[16-17]。文獻[18]采用RandlesECM擬合EIS，并根據模型中的三個電阻參數來檢測膜電極的水含量。文獻[19]建立PEMFC的ECM并使用電壓估計ECM的參數，再根據參數分析PEMFC退化的原因。文獻[20]根據EIS的高頻、中頻和低頻特性，建立了PEMFC完整的ECM，并根據該模型預測了不同操作條件下的阻抗。上述文獻為建立適當的ECM，通常需要對PEMFC的各反應動力學過程深入理解。然而由于所測試電池的性質和人為選擇的不同，建立的ECM也不同。甚至對于不同的操作條件，所需的ECM也不同。不同情況下，可以用不同的ECM描述同一個EIS，而他們的物理意義可能完全不 同[21]。這些都使ECM方法使用困難。

弛豫時間分布（Distribution of Relaxation Time, DRT）分析是另一種分析EIS的方法[22]。與ECM不同，DRT分析無需根據所測EIS建立相應的模型。其將PEMFC等效為無窮個RC（電阻與電容并聯）元件的串聯，并以RC元件表征各極化過程。通過求解DRT，可以確定PEMFC的各極化過程的時間常數及其分布[23]。文獻[24]首先對固體氧化物燃料電池的EIS進行去卷積，以獲得不同時間尺度下的極化過程分布。該方法最多可以分離三個物理上的不同過程。其后，文獻[25]首次將DRT應用在高溫質子交換膜燃料電池的性能分析中。設計了不同的實驗條件，并以此識別了DRT不同峰值所對應的極化過程。文獻[26]以PEMFC為對象，實驗過程中同時對陰陽極通入氫氣，揭示了陰極極化占總極化的96%。上述研究表明DRT分析在無特定的ECM的情況下，可以準確地分析PEMFC不同的極化過程。然而，目前尚無文獻借助DRT分析進行機車工況下PEMFC的性能衰退研究。相對于傳統分析工具，DRT分析可作為一種有效補充手段。

本文以動態機車工況下的PEMFC為對象，探究其運行不同時間后的性能；首先，采用極化曲線分析PEMFC的輸出性能。其次，根據所測EIS建立相應的ECM，并根據模型參數定量分析PEMFC的內部特性；最后，根據DRT分析PEMFC不同極化過程的變化。

1 PEMFC測試系統

PEMFC測試系統如圖1所示，該系統包括PEMFC、燃料電池測試臺和EIS分析儀。

圖1 PEMFC測試系統

本文測試對象為弗爾賽能源RDZ3-5K/25-V040燃料電池堆。該電堆由40片電池構成，每片電池活性面積為250cm2，額定電流為200A，額定功率5kW，最高運行溫度為65℃。本文采用了銳格RG- FCTS-15大功率燃料電池測試臺，該測試臺可控制PEMFC的負載電流、循環水溫度、氣體流量和吹掃周期等操作條件，可以設定所需循環工況并自動運行。采用FuelCon公司TrueData-EIS阻抗譜分析儀測量PEMFC的EIS，該分析儀可以測量不同負載下，寬頻率范圍的阻抗。

2 分析方法

本文針對PEMFC的EIS，建立相應的等效電路模型，根據模型參數對PEMFC的性能進行定量分析；對EIS數據進行DRT分析，用以對PEMFC的性質進行進一步分析。

2.1 電化學阻抗譜等效電路模型

對于不同的PEMFC，其所測得的EIS通常具有不同的形狀，但其組成部分相似。圖2為本文所研究PEMFC的一個典型EIS。

圖2 電化學阻抗譜

EIS由高頻弧、中頻弧及低頻弧組成。其中，高頻弧與質子傳輸過程有關，中頻弧與陰極活化過程有關，低頻弧與質量傳輸過程有關[27]。基于此，建立如圖3所示的3階ECM以表征PEMFC的EIS。

圖3阻抗可表示為

圖3 等效電路模型

式中，為電池的總阻抗；O、I、C和M分別為歐姆電阻、質子傳輸極化電阻、氧氣電荷傳輸極化電阻和質量傳輸極化電阻；Q1、Q2和Q3為常相角元件；Q1、Q2和Q3分別為對應的阻抗。I、C和M越大，表明其所對應的半圓弧的半徑越大。其中，常相角元件的阻抗可表示為[28]

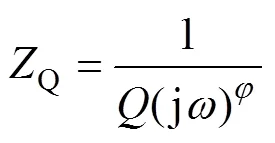
式中，為比例因子；為角頻率；為相角指數。

2.2 弛豫時間分布

文獻[24]首次通過DRT方法對固體氧化物燃料電池的EIS進行去卷積，以此分離出不同時間常數下的極化過程。EIS與DRT的關系可表示為[24]

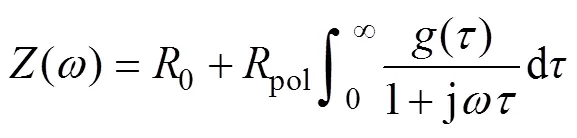
式中，()為阻抗數據；0為阻抗的歐姆部分；pol為阻抗的極化部分；()為各極化在總極化中的占比；為時間常數。

通常，對式（3）進行離散化處理，離散化公式為

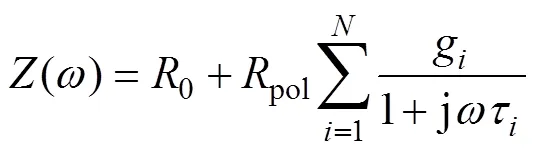
式（4）可將EIS視為一個電阻與無窮個RC（電阻與電容并聯）元件的組合，如圖4所示。其中，ti=RiCi。

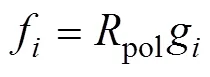
由于所測量的阻抗僅包含部分頻率，式（4）無法求出精確的解析解，通常采用正則化方法求其數值解。本文采用文獻[29]中提供的工具計算DRT。圖2對應的DRT如圖5所示。由圖5可知，DRT曲線主要由4個波峰（P1、P2、P3和P4）組成。袁浩等[23]分析了不同陰極/陽極過量系數，不同陰極/陽極進氣濕度對PEMFC各波峰的影響。陰極過量系數減小時，P1峰值增加明顯，陰極過量系數增加時，P2峰值減小明顯。而陽極過量系數改變時，P1和P2峰值變化都較小。陰極過量系數較低時，氧氣傳輸限制增加，陰極過量系數較高時，會導致反應物濃度較高，進而減小傳荷內阻。這表明P1與質量傳輸過程有關，P2與氧氣還原反應過程有關。陰極濕度較大時，P3和P4峰值有明顯下降，而陽極濕度改變時，P3和P4變化不明顯。顯然，濕度較大時，質子的傳導率增加。這表明P3和P4與陰極側的質子傳輸過程有關。由圖5可知，DRT方法可以獲得不同極化過程在頻率上的分布，且不需要事先掌握PEMFC的內在過程，無須對EIS建立等效電路模型。DRT方法可進一步解析高頻弧的極化過程，而ECM方法對高頻弧的細致分析往往存在困難。

3 實驗結果及分析

3.1 動態機車工況下老化實驗設計

本文旨在研究動態機車工況下，PEMFC性能的變化規律。操作條件設置為：電堆溫度60℃，陽極過量系數1.5，陰極過量系數3，陽極相對濕度0%，陰極相對濕度100%，吹掃周期10s。本文基于土耳其地鐵的實際工況，并簡化設計了如圖6所示的變電流循環工況。

一次循環中，20A持續48s，35A持續6s，80A持續52s，其余時間為0A，共持續200s。在實際測試中，電堆電流從0A直接拉升到80A時，氣體供應無法快速跟上，出現欠氣狀況，導致測試臺停機。為保證循環實驗能夠正常進行，在0～80A之間增加兩個電流階梯。

本文以2 000次循環（約110h）為一周期，進行性能測試。每2 000次循環后，分別測量了第1（電堆前端）、20（電堆中部）和40（電堆出口）片電池的極化曲線及相應的EIS。測試EIS時，負載電流設置為50A，以保證電池工作在歐姆區。所測EIS的頻率范圍為0.1Hz～10kHz，以指數形式采集50個頻率下的阻抗。

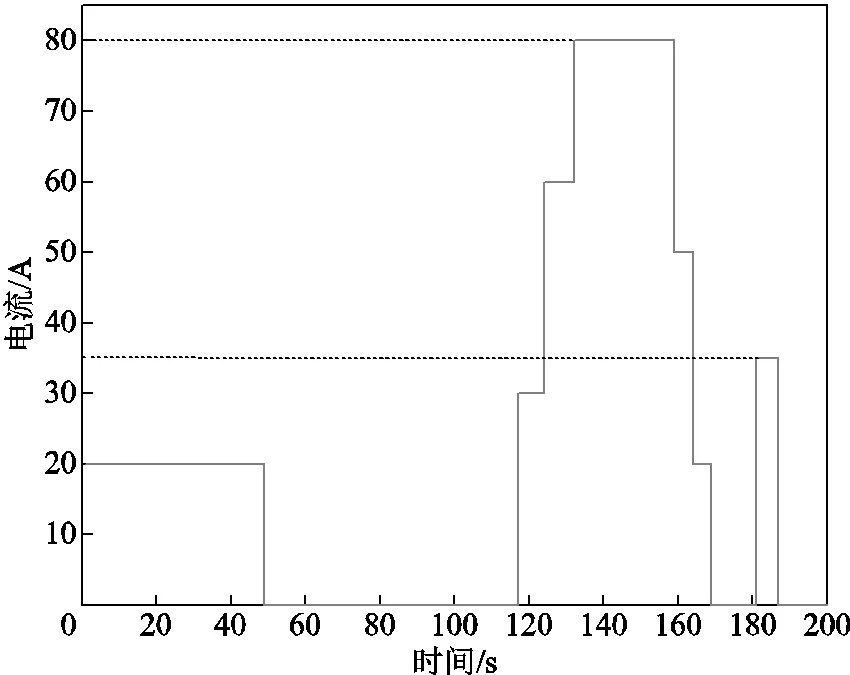
圖6 負載電流變化

3.2 不同單片電池極化曲線分析

初始狀態及固定間隔（0h、110h、220h、330h）后測量的極化曲線如圖7所示。為與EIS分析一致，下面以50A電流下各片電池電壓進行討論。

由圖7a可知，電池1隨著循環進行，性能不斷下降。0～110h、110～220h和220～330h期間的電壓衰減率分別為0.082mV/h、0.327mV/h和0.227mV/h。這表明電池1在0～110h期間的性能衰退較小，110～220h期間的性能衰退最嚴重。

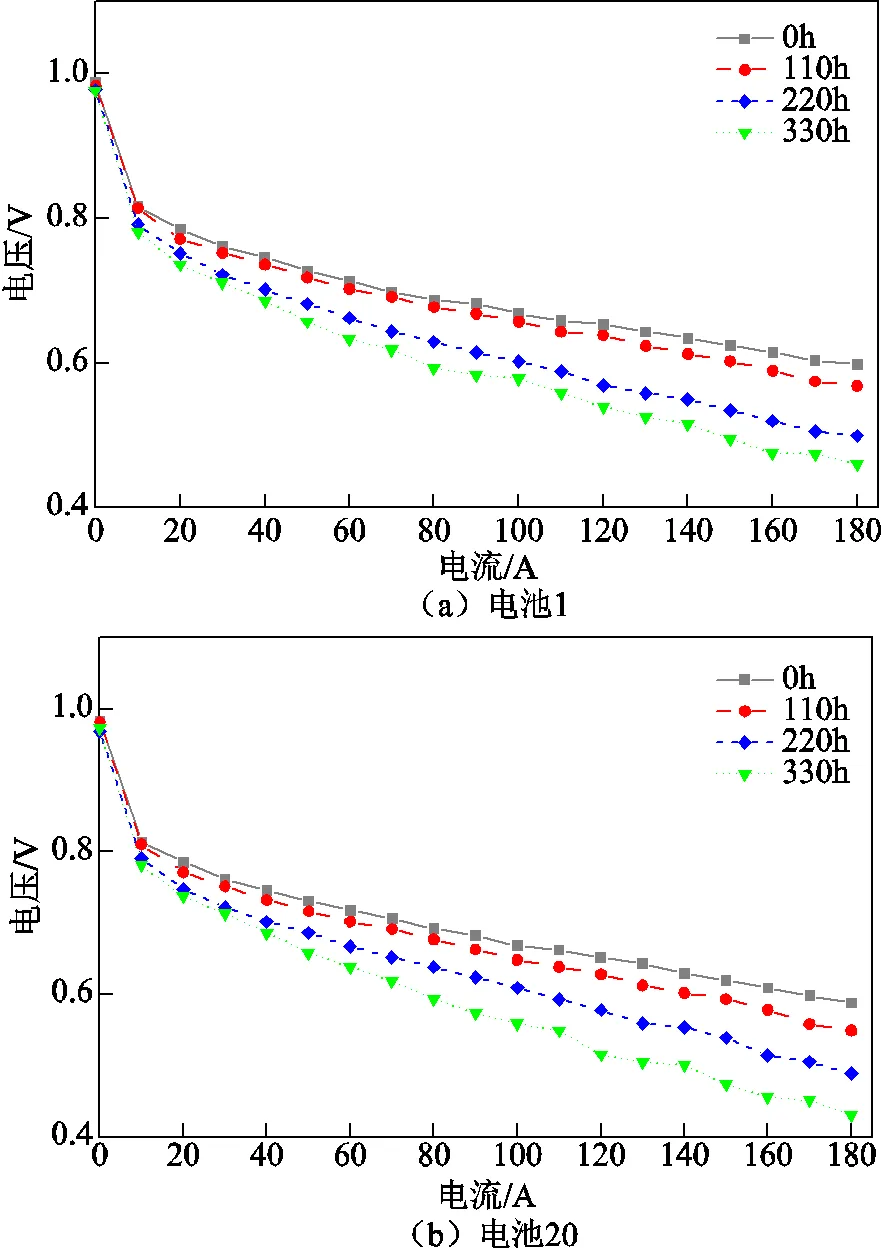
圖7 不同時間下電池1、電池20和電池40的極化曲線

Fig.7 Polarization curves of cell1, cell20 and cell40 at different time

由圖7b可知，電池20同樣隨著循環進行，性能不斷下降。該電池各階段的電壓衰減率分別為0.136mV/h、0.273mV/h和0.255mV/h。這表明電池20在0～110h期間的性能衰退最小，110～220h和220～330h期間的性能衰退接近。

由圖7c可知，電池40的性能并沒有隨循環的進行不斷下降，而在110h時的性能相較于0h有提升。該電池各階段的電壓衰減率分別為-0.064mV/h、0.191mV/h和0.273mV/h。這表明電池40在0～110h期間性能提升，220～330h期間的性能衰退最嚴重。由極化曲線可知，該電池在活化區0h的電壓降要大于110h。這可能是由于電池40位于電堆出口，初始測試時電池未活化完全。因此電流在0～180A間，0h的輸出性能差于110h。然而極化曲線的歐姆區內，110h的斜率絕對值要大于0h。可以預見，更大電流下110h的性能要差于0h。

3.3 不同單片電池電化學阻抗譜分析

圖8為3片電池的EIS及等效電路擬合曲線，可以看出三片電池總的EIS弧都隨時間增大。

由圖8a可知，電池1的EIS弧在110～220h期間的增長最大，表明該段時間電池性能衰退最嚴重。在0～110h及220～330h期間EIS弧的增長都小于110～220h。

由圖8b可知，電池20的EIS在0～110h期間增長最小，110～220h及220～330h期間EIS弧的增加相差較小。

由圖8c可知，電池40的EIS在0～220h期間的衰減較小，與該電池未活化完全有關。220～330h期間的增長最大，表明該段時間電池性能衰退最嚴重。上述各片電池EIS弧的變化趨勢與圖7中各自極化曲線對應。然而，僅通過EIS弧只能定性分析PEMFC性能的變化。為定量分析EIS弧的變化，對電池的等效電路模型參數進行分析。由2.1節等效電路模型擬合EIS數據，相應的等效電路參數如圖9所示。由圖9可知，三片電池的C占主導，且隨著循環進行，C不斷增加。

由圖9a可知，電池1的C從110h的0.374mW·cm2增加到220h的0.570mW·cm2，在0～110h及220～330h期間的增量較小。這表明該電池在110～220h期間產生的衰退最嚴重。220h后，I明顯增大，表明質子傳輸阻礙增大。由圖8a可知，220h后高頻環出現明顯的小圓弧。

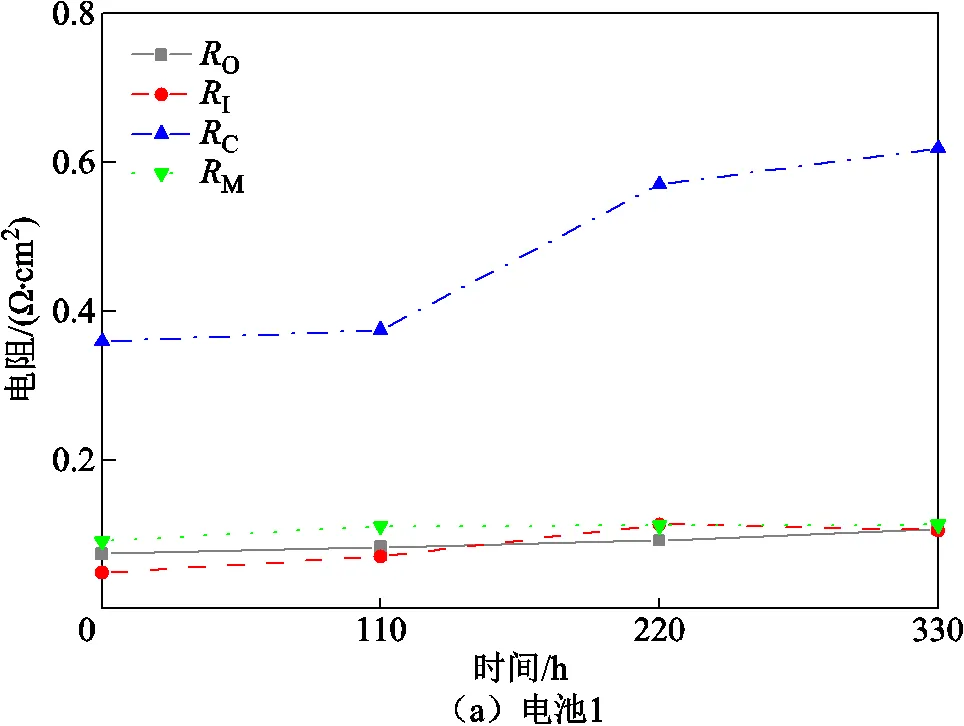
由圖9b可知，電池20的C在0～110h期間增長了0.020mW·cm2，110～220h期間增長了0.083mW·cm2，220～330h期間增長了0.197mW·cm2。該增長表明電池的衰退速率逐步加快。與電池1類似，該電池的I由110h的0.058mW·cm2增加到了220h的0.104mW·cm2。這表明該電池在該階段質子傳輸阻礙增大，且在圖8b中表現為高頻區域在220h后出現明顯的小圓弧。

由圖9c可知，電池40的C在220～330h期間增長最多，達到了0.205mW·cm2。這表明電池40在220～330h期間的衰退最嚴重。0h的I大于110h的，表明0h的質子傳輸阻礙大于110h的，該結果與極化曲線相對應。

3.4 不同單片電池弛豫時間分布分析

考慮到實測EIS有干擾數據，采用3.3節中擬合EIS來求解其DRT，相應的DRT曲線如圖10所示。由圖10可知，3片電池的DRT曲線的4個波峰P1、P2、P3和P4的峰值分別出現在10Hz、100Hz、1kHz和10kHz附近。其中，P1和P2峰值遠大于P3和P4，表明電池的質量傳輸和氧氣還原反應的極化過程為主要極化過程。

圖10 不同時間下電池1、20和電池40的DRT

由圖10a可知，電池1的P1峰值在0～220h期間逐漸增大，表明氧氣的傳輸阻礙逐漸增加。330h時，P1峰值減小，表明此時傳質阻礙減小。該現象可能與氣體擴散層衰退導致的孔隙率增加有關。P2峰值隨著時間的增加而增大，表明氧氣還原過程的阻礙增加，這與催化劑的衰退有關。

由圖10b可知，電池20的P1峰值變化與電池1相同。且由圖9b可知，電池20的M從220h的0.093mW·cm2減少到了330h的0.038mW·cm2。該變化與DRT的P1峰值變化相吻合。P2峰值逐漸增加，表明氧氣還原反應阻礙增加，與其C的變化相吻合。P3峰值在0～220h期間逐漸增大，330h時有減小。相應地，由圖9b可知，I從220h的0.104mW·cm2減少到了330h的0.102mW·cm2。

由圖10c可知，電池40的P1峰值在110h和330h時大于0h和220h，這可能與電池未完全活化有關。P2峰值隨著時間增加而增大，表明其氧氣還原反應阻礙增加。330h的P3峰值顯著大于之前，與I從220h的0.061mW·cm2增加到了330h的0.125mW·cm2相對應。

3片電池的P3和P4峰值整體上呈現增加的趨勢，表明電池的質子傳輸阻礙逐漸增加。相對于ECM方法，DRT分析將高頻過程更細致地分為P3及P4，有助于理解EIS中易被覆蓋的高頻過程。然而，氧氣還原反應的電荷轉移動力學與電極中質子傳輸的耦合，以及氧氣還原反應的復雜機制都可能會對P3和P4峰值產生影響[30]。因此，對高頻極化過程還需進一步研究。

4 結論

本文結合極化曲線、ECM和DRT方法，對動態機車工況下PEMFC電堆第1、20、40片電池在0h、110h、220h及330h的性能進行分析。結果表明，電堆各單片電池的陰極極化過程為主要極化過程，但電堆不同位置電池的衰退趨勢呈現明顯的不一致性。電堆入口的電池1在110～220h期間衰退速率最快，電堆中部的電池20衰退速率逐漸加快，電堆出口電池40在220～330h期間衰退速率最快。特別地，由于電堆出口可能的供氣不足，導致電池40在初始時未完全活化，活化損耗較大。從極化曲線可以看到，該電池在歐姆區110h的輸出性能好于220h的性能。通過三種方法對PEMFC電堆進行衰退性能分析，能全面地分析其衰退趨勢，為PEMFC的健康狀態管理及壽命預測提供依據。

[1] 陳維榮, 錢清泉, 李奇. 燃料電池混合動力列車的研究現狀與發展趨勢[J]. 西南交通大學學報, 2009, 44(1): 1-6.

Chen Weirong, QianQingquan, Li Qi. Investigation status and development trend of hybrid power train based on fuel cell[J]. Journal of Southwest Jiaotong University, 2009, 44(1): 1-6.

[2] 肖麗, 高峰, 侯淑萍, 等. 新能源汽車驅動系統速度傳感器故障檢測與容錯控制法[J]. 電工技術學報, 2020, 35(24): 5075-5086.

Xiao Li, Gao Feng, Hou Shuping, et al. Speed sensor fault detection and tolerant control for new energy vehicle drive system[J]. Transactions of China Elec- trotechnical Society, 2020, 35(24): 5075-5086.

[3] 潘光勝, 顧偉, 張會巖, 等. 面向高比例可再生能源消納的電氫能源系統[J]. 電力系統自動化, 2020, 44(23): 1-10.

Pan Guangsheng, Gu Wei, Zhang Huiyan, et al. Electricity and hydrogen energy system towards accomodation of high proportion of renewable energy[J]. Automation of Electric Power Systems, 2020, 44(23): 1-10.

[4] Chen Huicui, Pei Pucheng, Song Mancun. Lifetime prediction and the economic lifetime of Proton Exchange Membrane fuel cells[J]. Applied Energy, 2015, 142: 154-163.

[5] 李爭, 張蕊, 孫鶴旭, 等. 可再生能源多能互補制-儲-運氫關鍵技術綜述[J]. 電工技術學報, 2021, 36(3): 446-462.

Li Zheng, Zhang Rui, Sun Hexu, et al. Review on key technologies of hydrogen generation, storage and transportation based on multi-energy complementary renewable energy[J]. Transactions of China Electro- technical Society, 2021, 36(3): 446-462.

[6] 戚志東, 裴進, 胡迪. 基于分數階PID控制的質子交換膜燃料電池前級功率變換器[J]. 電工技術學報, 2019, 34(增刊1): 235-243.

Qi Zhidong, Pei Jin, Hu Di. Pre-stage power converter of proton exchange membrane fuel cell based on fractional order PID controller[J]. Transactions of China Electrotechnical Society, 2019, 34(S1): 235- 243.

[7] Lin R, Li B, Hou Y P, et al. Investigation of dynamic driving cycle effect on performance degradation and micro-structure change of PEM fuel cell[J]. Inter- national Journal of Hydrogen Energy, 2009, 34(5): 2369-2376.

[8] Schmittinger W, Vahidi A. A review of the main parameters influencing long-term performance and durability of PEM fuel cells[J]. Journal of Power Sources, 2008, 180(1): 1-14.

[9] Meyer Q, Ronaszegi K, Robinson J B, et al. Com- bined Current and temperature mapping in an air- cooled, open-cathode polymer electrolyte fuel cell under steady-state and dynamic conditions[J]. Journal of Power Sources, 2015, 297: 315-322.

[10] Mezzi R, Yousfi-Steiner N, Péra M C, et al. An Echo State Network for fuel cell lifetime prediction under a dynamic micro-cogeneration load profile[J]. Applied Energy, 2021, 283: 116297.

[11] Tian Xinlong, Luo Junming, Nan Haoxiong, et al. Transition metal nitride coated with atomic layers of Pt as a low-cost, highly stable electrocatalyst for the oxygen reduction reaction[J]. Journal of the American Chemical Society, 2016, 138(5): 1575-1583.

[12] Galeano C, Meier J C, Peinecke V, et al. Toward highly stable electrocatalysts via nanoparticle pore confinement[J]. Journal of the American Chemical Society, 2012, 134(50): 20457-20465.

[13] Jayasayee K, Veen J A R V, Manivasagam T G, et al. Oxygen reduction reaction (ORR) activity and dura- bility of carbon supported PtM (Co, Ni, Cu) alloys: influence of particle size and non-noble metals[J]. Applied Catalysis B: Environmental, 2012, 111/112: 515-526.

[14] Liu Yongfeng, Fan Lei, Pei Pucheng, et al. Asympto- tic analysis for the inlet relative humidity effects on the performance of proton exchange membrane fuel cell[J]. Applied Energy, 2018, 213: 573-584.

[15] 張雪霞, 蔣宇, 黃平, 等. 質子交換膜燃料電池容錯控制方法綜述[J]. 中國電機工程學報, 2021, 41(4): 1431-1444.

Zhang Xuexia, Jiang Yu, Huang Ping, et al. A review of fault-tolerant control methodology on proton exchange membrane fuel cell[J]. Proceedings of the CSEE, 2021, 41(4): 1431-1444.

[16] Rezaei Niya S M, Hoorfar M. Study of proton exchange membrane fuel cells using electrochemical impedance spectroscopy technique-a review[J]. Journal of Power Sources, 2013, 240: 281-293.

[17] 吳健, 尹澤, 李豪, 等. 基于分數階理論的鋰離子電池高頻等效電路模型[J]. 電工技術學報, 2021, 36(18): 3902-3910.

Wu Jian, Yin Ze, Li Hao, et al. High-frequency equivalent circuit model of lithium-ion battery based on fractional order theory[J]. Transactions of China Electrotechnical Society, 2021, 36(18): 3902-3910.

[18] Fouquet N, Doulet C, Nouillant C, et al. Model based PEM fuel cell state-of-health monitoring via AC impedance measurements[J]. Journal of Power Sources, 2006, 159(2): 905-913.

[19] Kim T, Oh H, Kim H, et al. An online-applicable model for predicting health degradation of PEM fuel cells with root cause analysis[J]. IEEE Transactions on Industrial Electronics, 2016, 63(11): 7094-7103.

[20] Rezaei Niya S M, Hoorfar M. Process modeling of electrodes in proton exchange membrane fuel cells[J]. Journal of Electroanalytical Chemistry, 2015, 747: 112-122.

[21] 曹楚南, 張鑒清. 電化學阻抗譜導論[M]. 北京: 科學出版社, 2002.

[22] 王佳, 黃秋安, 李偉恒, 等. 電化學阻抗譜弛豫時間分布基礎[J]. 電化學, 2020, 26(5): 607-627.

Wang Jia, Huang Qiuan, Li Weiheng, et al. Funda- mentals of distribution of relaxation times for elec- trochemical impedance spectroscopy[J]. Journal of Electrochemistry, 2020, 26(5): 607-627.

[23] 袁浩, 戴海峰, 杜潤本, 等. 質子交換膜燃料電池電化學阻抗譜弛豫時間分布研究[J]. 機械工程學報, 2020, 56(22): 120-130.

Yuan Hao, Dai Haifeng, Du Runben, et al. Dis- tribution of relaxation times analysis of proton exchange membrane fuel cell electrochemical impedance spectra[J]. Journal of Mechanical Engineering, 2020, 56(22): 120-130.

[24] Schichlein H, Müller A, Voigts M, et al. Decon- volution of electrochemical impedance spectra for the identification of electrode reaction mechanisms in solid oxide fuel cells[J]. Journal of Applied Elec- trochemistry, 2002, 32: 875-882.

[25] Wei? A, Schindler S, Galbiati S, et al. Distribution of relaxation times analysis of high-temperature PEM fuel cell impedance spectra[J]. Electrochimica Acta, 2017, 230: 391-398.

[26] Heinzmann M, Weber A, Ivers-Tiffée E. Advanced impedance study of polymer electrolyte membrane single cells by means of distribution of relaxation times[J]. Journal of Power Sources, 2018, 402: 24- 33.

[27] Dhirde A M, Dale N V, Salehfar H, et al. Equivalent electric circuit modeling and performance analysis of a PEM fuel cell stack using impedance spectroscopy[J]. IEEE Transactions on Energy Conversion, 2010, 25(3): 778-786.

[28] Yuan Xiaozi, Wang Haijiang, Sun J C, et al. AC impedance technique in PEM fuel cell diagnosis-a review[J]. International Journal of Hydrogen Energy, 2007, 32(17): 4365-4380.

[29] Wan Tinghei, Saccoccio M, Chen Chi, et al. Influence of the discretization methods on the distribution of relaxation times deconvolution: implementing radial basis functions with DRT tools[J]. Electrochimica Acta, 2015, 184: 483-499.

[30] Liu Yuxiu, Murphy M W, Baker D R, et al. Proton conduction and oxygen reduction kinetics in PEM fuel cell cathodes: effects of ionomer-to-carbon ratio and relative humidity[J]. Journal of the Electro- chemical Society, 2009, 156(8): B970.

Degradation Performance Analysis of Proton Exchange Membrane Fuel Cell Stack under Dynamic Locomotive Conditions

（School of Electrical Engineering Southwest Jiaotong University Chengdu 611756 China）

To explore the degradation performance of proton exchange membrane fuel cell (PEMFC) stack under dynamic locomotive conditions, polarization curve, equivalent circuit model (ECM) method, and distribution of relaxation time (DRT) method are combined to analyze the performance of PEMFC. For the 5kW stack, the polarization curves and electrochemical impedance spectroscopy (EIS) of the 1st, 20th, and 40th cells after 0h, 110h, 220h, and 330h of locomotive operation are measured. The third-order equivalent circuit model of PEMFC is established, and the internal changes of PEMFC are analyzed according to the model parameters. The DRT corresponding to EIS is calculated to explain the changes of the polarization process of PEMFC according to different peaks. The results show that the main losses of different cells occur in the oxygen reduction reaction process and mass transfer process, while the degradation trends of different cells are inconsistent under dynamic conditions. Cell 1 at the stack inlet degrades the fastest during 110～220h. The degradation rate of cell 20 increases with time. Cell 40 at stack outlet degrades the fastest during 220～330h. Due to cell 40 is not fully activated at 0h, its performance is improved during 0～110h.

Dynamic locomotive conditions, proton exchange membrane fuel cell, stack degradation, electrochemical impedance spectroscopy, inconsistency

10.19595/j.cnki.1000-6753.tces.211132

TM911.4

國家自然科學基金青年科學基金（51607149）、四川省重點研究開發計劃（22ZDYF3375）、四川省科技計劃項目應用基礎研究（2019YJ0236）、磁浮技術與磁浮列車教育部重點實驗室2018年度開放課題、2022年度西南交通大學基礎研究培育支持計劃項目學科交叉專項（2682022ZTPY024）、2021年度成都西南交通大學國家軌道交通電氣化與自動化工程技術研究中心開放課題基金（面上）計劃（NEEC-2022-B010）資助。

2021-07-23

2021-09-22

張雪霞 女，1979年生，副教授，博士生導師，研究方向為電力系統及其自動化、燃料電池技術與應用和智能優化算法。E-mail: survival_zxx@sina.com（通信作者）

黃 平 男，1996年生，碩士研究生，研究方向為燃料電池技術與應用。E-mail: huangping@my.swjtu.edu.cn

（編輯 郭麗軍）