具有時(shí)滯效應(yīng)的SIS模型的動(dòng)力學(xué)分析①
劉志華, 曹慧, 徐河苗
1.陜西科技大學(xué) 數(shù)學(xué)與數(shù)據(jù)科學(xué)學(xué)院,西安 710029; 2.長(zhǎng)治學(xué)院 數(shù)學(xué)系,山西 長(zhǎng)治 046011
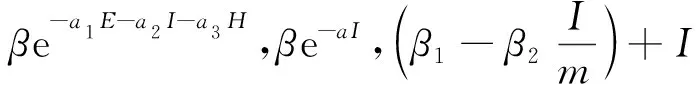
1 模型的建立
以流感背景,并基于經(jīng)典的SIS傳染病模型,將媒體報(bào)道的染病人數(shù)對(duì)疾病發(fā)生率的影響用函數(shù)e-αI(t-τ)來(lái)刻畫,建立如下的模型:
(1)
其中:S(t)和I(t)分別表示t時(shí)刻的易感染者和染病者人數(shù),Λ表示易感者的常數(shù)輸入率,μ表示自然死亡率,γ表示染病者的恢復(fù)率.
2 模型的適定性與平衡點(diǎn)
在本節(jié)中,我們將先分析模型(1)的解的非負(fù)性和有界性,再借助極限系統(tǒng)理論給出平衡點(diǎn)的存在性.

事實(shí)上,由模型(1)中的第二個(gè)方程直接計(jì)算可得
顯然,I(t)≥0,t∈(0,τ]. 進(jìn)而,類似計(jì)算得
以上分析說(shuō)明,對(duì)于任意非負(fù)初值,必有I(t)≥0,t≥0成立.
下面說(shuō)明S(t)≥0,t≥0成立. 假設(shè)?t1>0,使得S(t)>0,t∈(0,t1),S(t1)=0,且S(t)>0,t>t1. 則有
與S(t)<0,t>t1矛盾. 也就是假設(shè)不成立. 即S(t)≥0,t≥0成立.
以上分析說(shuō)明,模型(1)中任意具有非負(fù)初值的解一定是非負(fù)的. 下面來(lái)說(shuō)明模型(1)解的有界性.將模型(1)中的兩個(gè)方程相加可得

(2)
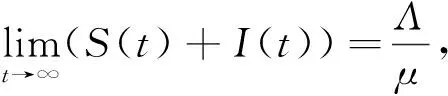
另外,利用再生矩陣的辦法[15]可以得到模型(1)的基本再生數(shù)為
將S(t)=N*-I(t)代入模型(1),可得模型(1)的極限模型
(3)
利用極限系統(tǒng)理論可知[16],模型(3)與模型(1)有相同的動(dòng)力學(xué)性態(tài). 接下來(lái)的研究將借助模型(3)來(lái)分析模型(1)的動(dòng)力學(xué)性態(tài).
(4)
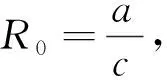
顯然,模型(4)始終有零平衡點(diǎn)X0=0. 為了找到模型(4)的正平衡點(diǎn)X*,令
f(X)=ae-bX(1-X) ,X∈[0, 1]
通過(guò)直接計(jì)算可得:f(0)=a,f(1)=0,且f′(X)<0,這說(shuō)明a>c時(shí),也就是,當(dāng)R0>1時(shí),模型(4)存在唯一的正平衡點(diǎn)X*,滿足ae-bX*(1-X*)=c.即下面的定理成立:
定理1模型(4)始終存在零平衡點(diǎn)X0=0,并且當(dāng)R0>1時(shí),模型(4)還存在唯一的正平衡點(diǎn)X*,滿足ae-bX*(1-X*)=c.
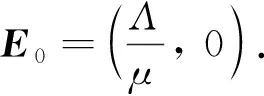
下面研究模型(4)的零平衡點(diǎn)和正平衡點(diǎn)的穩(wěn)定性.
定理2如果R0<1,模型(4)的零平衡點(diǎn)X0是全局漸近穩(wěn)定的; 如果R0>1,X0是不穩(wěn)定的.
證直接計(jì)算可得,模型(4)在X0=0處的特征方程為
λ-a+c=0
(5)
即λ=c(R0-1). 由Hurwitz判據(jù)可知,若R0<1,有λ<0,即模型(4)的零平衡點(diǎn)是局部漸近穩(wěn)定的.若R0>1,則λ>0,這說(shuō)明模型(4)的零平衡點(diǎn)是不穩(wěn)定的.
下面來(lái)證明零平衡點(diǎn)的全局穩(wěn)定性. 記V1(t)=X(t),則
(6)
顯然,當(dāng)R0<1時(shí),V′1|(4)<0,故模型(4)的零平衡點(diǎn)是全局漸近穩(wěn)定的. 證畢.
定理3如果R0>1,τ=0,那么模型(4)的正平衡點(diǎn)X*是全局漸近穩(wěn)定的.
證直接計(jì)算可知,模型(4)在X=X*處的特征方程為
(7)
當(dāng)τ=0時(shí),特征方程(7)可重新寫為
(8)
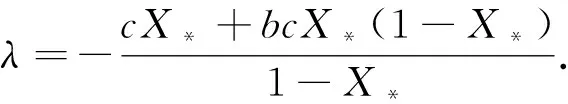
(9)
由于y=e-bX是一個(gè)遞減函數(shù),因此,有(X-X*)(e-bX-e-bX*)<0成立. 也就是,V′2|(4)≤0. 另外,當(dāng)且僅當(dāng)X=X*時(shí),V′2|(4)=0. 這說(shuō)明M={X|V′2(x)=0}={X*},也就是,模型(4)在M上的最大不變集就是{X*}.根據(jù)LaSsalle不變集原理可知,當(dāng)R0>1時(shí),模型(4)的正平衡點(diǎn)X*是全局漸近穩(wěn)定的. 證畢.
由定理2和定理3可知,當(dāng)R0<1時(shí),模型(1)的無(wú)病平衡點(diǎn)E0和地方病平衡點(diǎn)E*是全局漸近穩(wěn)定的.
3 Hopf分支
在本小節(jié)中將討論τ>0時(shí),模型(4)可能發(fā)生的Hopf分支. 為此,假設(shè)λ=iω,ω>0,代入方程(7)可得
(10)
進(jìn)而有
(11)
也即
(12)
如果方程(12)有一個(gè)正根ω0,則正平衡點(diǎn)X*的穩(wěn)定性可能會(huì)隨著τ的改變而改變. 為此,記c*=e-bX*,則當(dāng)b>1且c*>e1-b時(shí),方程(12)存在一個(gè)正根
(13)
進(jìn)而可得
(14)
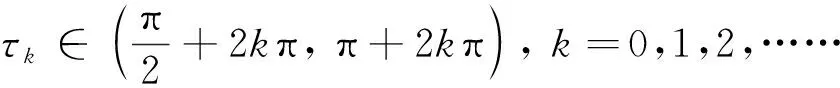
因此,
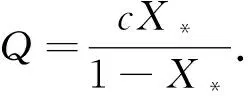
(15)
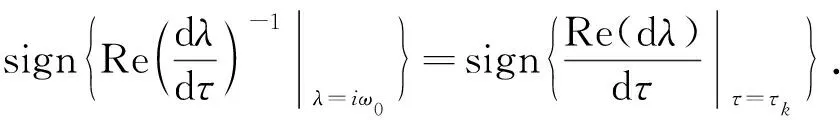
利用泛函微分方程的Hopf分支理論[17],得到下面的結(jié)論.
定理4假設(shè)R0>1,
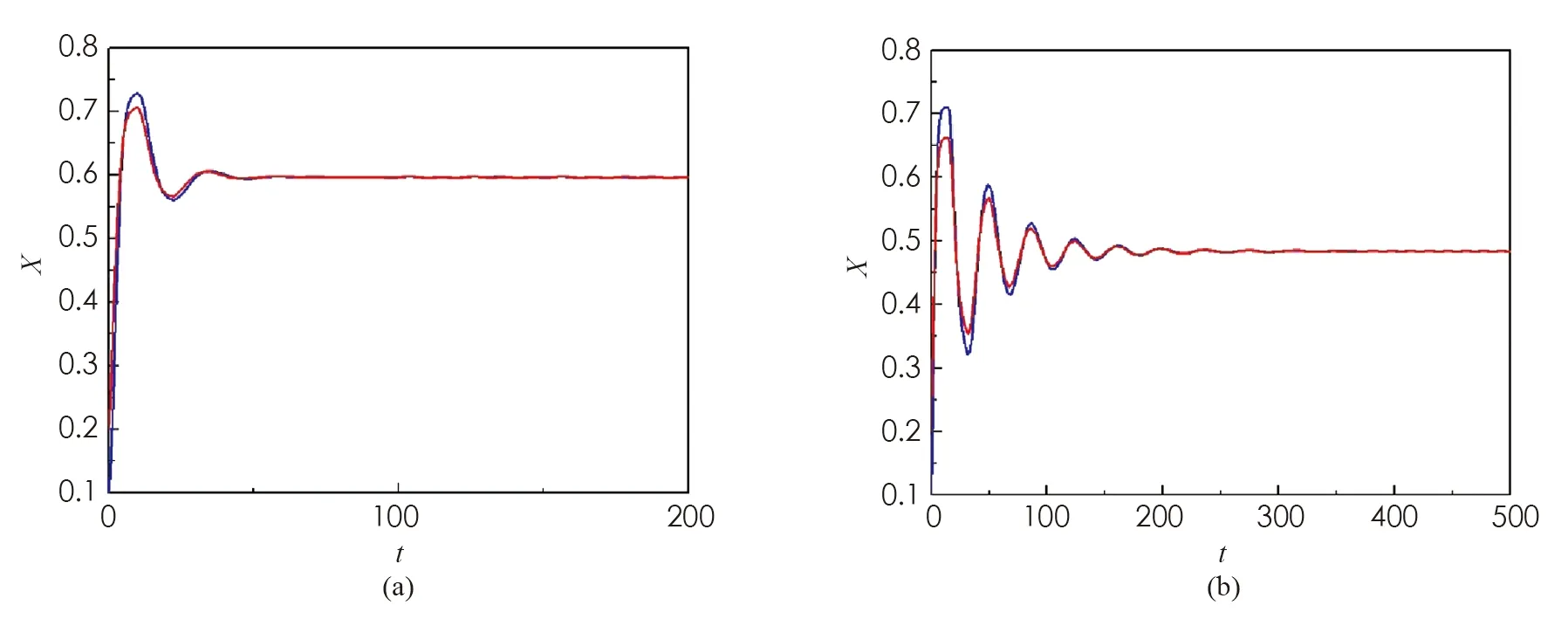
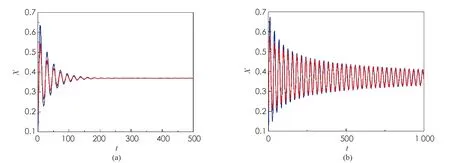
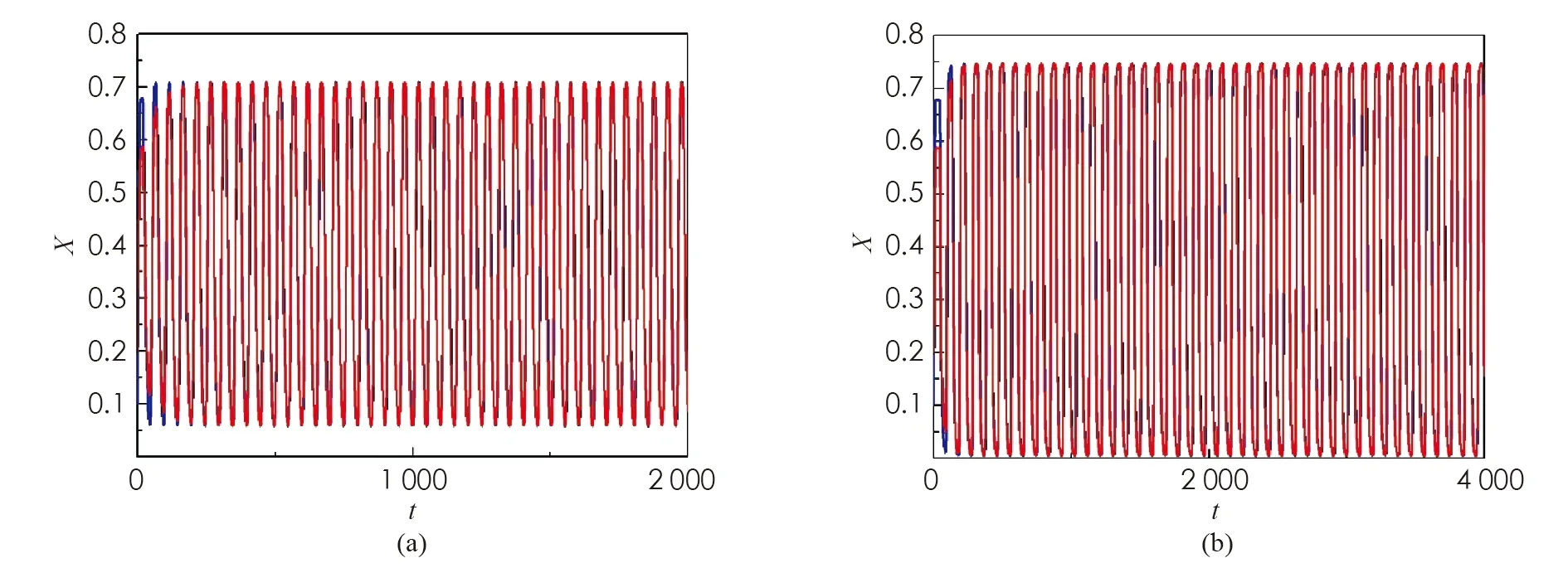
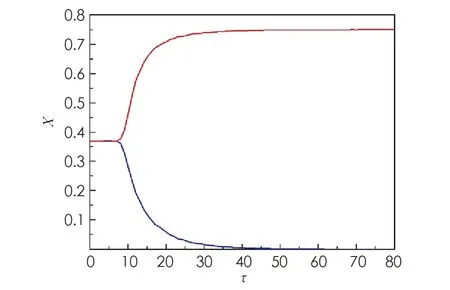
(1) 若0 (2) 若b>1,c*≤e1-b,則對(duì)任意τ≥0,模型(4)的正平衡點(diǎn)X*是漸近穩(wěn)定的; (3) 若b>1,c*>e1-b,則對(duì)任意τ∈[0,τ0],模型(4)的正平衡點(diǎn)X*是漸近穩(wěn)定的; (4) 若b>1,c*>e1-b,則對(duì)任意τ≥τ0,正平衡點(diǎn)X*是漸近穩(wěn)定的; 且在τ=τk,k=0,1,2…時(shí),模型(4)會(huì)在X*處發(fā)生Hopf分支. 在本小節(jié)中,將利用文獻(xiàn)[18-19]中的全局Hopf分支理論來(lái)討論模型(4)產(chǎn)生的局部Hopf分支的全局延拓問(wèn)題. 為此,引入變換y(t)=x(τt),模型(4)可被改寫為 y′(t)=F(yt,τ,T)F(yt,τ,T)∈X×R×R+ (16) 這里yt(θ)=y(t+θ),θ∈[-1,0],yt∈X,X=C([-1,0],T),并且 y′(t)=τae-by(t-1)(1-y(t))y(t)-τcy(t) (17) 引入下面的記號(hào): ∑=Cl{(y,τ,T):y是方程(17)的T周期解}∈X×R×R+ 引理1方程(17)的所有周期解是一致有界的. 證設(shè)y(t)是方程(17)的一個(gè)非平凡的周期解,且令y(t1)=N和y(t2)=n分別為其最大值和最小值,滿足0 ((1-N)ae-by(t1-1)-c)N=0 (18) ((1-n)ae-by(t2-1)-c)n=0 (19) 引理2如果b>1,且c*>e1-b滿足,方程(17)沒(méi)有周期為1或2的周期解[19]. 證方程(17)的任意非平凡的周期為1周期解為u(t),且為如下常微分方程的非平凡周期解: u′(t)=τ(ae-bu(1-u-c))u (20) 由于一階純量常微分方程不存在非平凡周期解,故(20)式不存在周期解. 若(17)式有周期為2的非平凡周期解u(t),則u1(t)=u(t),u2(t)=u(t-1),并且滿足 (21) 由(21)式與y(t)相對(duì)應(yīng)的周期軌道包含在如下區(qū)域: 則對(duì)所有的(u1,u2)∈G1總存在 因此由Bendixson周期解不存在準(zhǔn)則[20]知(21)式?jīng)]有平凡周期解. 證畢. 證設(shè)y(t)為方程(17)的周期為4的周期解,并令ui(t)=y(t-i+1),i=1,2,3,4. 于是u(t)=(u1(t),u2(t),u3(t),u4(t))是下述常微分方程的周期: (22) 由引理1可知(22)式與y(t)相對(duì)應(yīng)的周期軌道包含在如下區(qū)域: (23) 解的一致有界性表明所有周期解均位于G2內(nèi),為了說(shuō)明方程(17)沒(méi)有4的周期解,只需證明方程(17)在區(qū)域G2中不存在周期解即可. 那么為證明方程(17)在區(qū)域G2中不存在周期解,我們將應(yīng)用高維常微分方程Bendixson準(zhǔn)則[20]得到方程(22)右端的Jacobi矩陣為 (24) 這里記Ai=c-a(1-2ui)e-bui+1,Bi=abui(1-ui)e-bui+1,u5=u1,i=1,2,3,4. 下面對(duì)R6選取向量模: 其中(i,j)∈{(1,4),(2,1),(3,2),(4,3)},(p,q)∈{(1,3),(2,4)}. 要使μ(J[2](u))<0,當(dāng)且僅當(dāng)對(duì)所有u∈G2,使得 (25) (26) 進(jìn)一步有 因此,應(yīng)用文獻(xiàn)[20]中的推論3.5可得方程組(22)不存在周期為4的周期解. 證畢. 定理51) 如果R0>1,b>1,且c*>e1-b,則對(duì)任意τ>τ1,方程(17)至少有一個(gè)非平凡的周期解. 對(duì)τ∈[τk-δk,τk+δk]成立,且 Ωεk={(u,T)|0 所以, 在本小節(jié)中,將借助數(shù)值模擬來(lái)驗(yàn)證所得理論結(jié)果的合理性. 為此,令a=1.2,c=0.3. 下面分情況討論. 當(dāng)b=0.8<1,τ=10時(shí),如圖1(a)所示,模型(4)從不同初值出發(fā)的解最終都趨近于正平衡點(diǎn)X*,這說(shuō)明X*是穩(wěn)定的. 當(dāng)b=1.5>1時(shí),直接計(jì)算得e1-b=0.606 5>c*. 令τ=15,則X*仍是穩(wěn)定的,見(jiàn)圖1(b). 圖1 b=0.8,τ=10時(shí)模型(4)平衡點(diǎn)X*的穩(wěn)定性 當(dāng)b=2.5>1時(shí),e1-b=0.223 1 圖2 b=2.5,τ=8時(shí)模型(4)平衡點(diǎn)X*的穩(wěn)定性 下面展示平衡點(diǎn)X*處的Hopf分支的全局延拓性. 此時(shí)令a=1.2,b=2.5,c=0.3,相應(yīng)地,平衡點(diǎn)X*=0.369 8,R0=4>1,c*=0.396 7.通過(guò)(13)和(14)式計(jì)算得τ0=8.517 9,τ1=37.833 8. 當(dāng)b=2.5,并且分別滿足定理5的條件1)和2)時(shí),各自選取τ=40>τ1,τ=20>τ0,如圖3(a),(b)所示,兩張圖都展示了在平衡點(diǎn)X*附近從τ0分支出的周期解是大范圍存在的. 圖3 模型(4)在平衡點(diǎn)X*處的大范圍周期解 相應(yīng)地, 隨著時(shí)滯τ的不斷增加,模型(4)在平衡點(diǎn)X*處展現(xiàn)出了Hopf分支(圖4). 圖4 系統(tǒng)(4)在平衡點(diǎn)X*處的Hopf分支圖 在本小節(jié)中,主要研究了媒體報(bào)道的染病者數(shù)量對(duì)SIS模型動(dòng)力學(xué)性態(tài)的影響. 給出了模型(1)的基本再生數(shù),借助極限系統(tǒng),討論了系統(tǒng)(4)平衡點(diǎn)的存在性、穩(wěn)定性,以及平衡點(diǎn)不穩(wěn)定時(shí)可能發(fā)生的Hopf分支. 當(dāng)R0<1時(shí),模型(1)存在全局漸近穩(wěn)定的無(wú)病平衡點(diǎn); 而當(dāng)R0>1時(shí),模型(1)存在唯一的地方病平衡點(diǎn), 并且地方病平衡點(diǎn)的穩(wěn)定性會(huì)隨著時(shí)滯τ的增加而發(fā)生改變,即:在τ=0的情況下,地方病平衡點(diǎn)是全局漸近穩(wěn)定的; 當(dāng)τ>τ0時(shí),地方病平衡點(diǎn)不再穩(wěn)定,并會(huì)發(fā)生全局延拓的Hopf分支.我們也給出了發(fā)生全局Hopf分支延拓的條件. 系統(tǒng)(4)中的參數(shù)b=αN*,通過(guò)改變b的參數(shù)值大小,可以明顯看出b值對(duì)平衡點(diǎn)的影響.也就是說(shuō), 由媒體報(bào)道的染病者數(shù)量所引起的時(shí)滯效應(yīng)會(huì)使得模型的動(dòng)力學(xué)性態(tài)更加豐富. 即媒體報(bào)道引起的時(shí)滯效應(yīng)會(huì)改變地方病平衡點(diǎn)的穩(wěn)定性,產(chǎn)生全局Hopf分支.3.1 全局Hopf分支的存在性
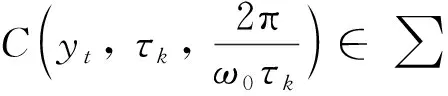
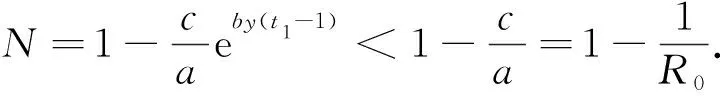
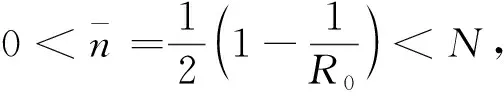
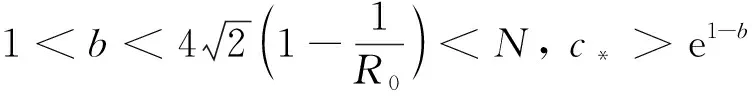
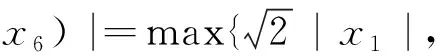
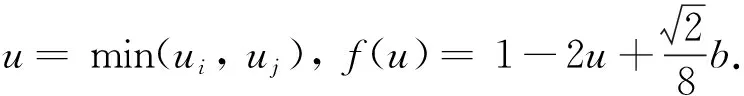
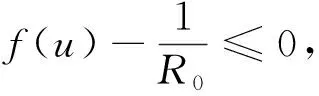
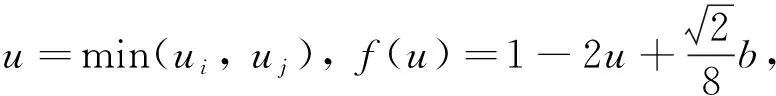
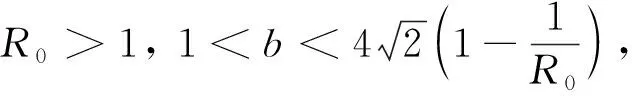
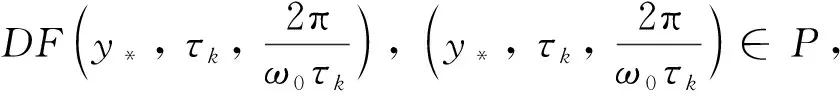

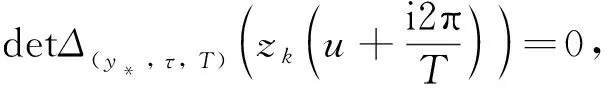
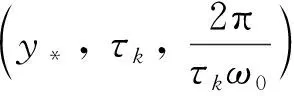
4 數(shù)值模擬
5 總結(jié)

