水準網線性混合效應模型建立與參數估計研究

陳軍紅，王炳燕

(1.西安建筑科技大學華清學院 土工程學院，陜西 西安 710043；2.海南靈宇地理信息有限公司，海南 571138)

0 引言

隨著各地城市建設加快發展，城市規模不斷擴大，中高層建筑越來越多。在這種發展形勢下，樓層的增加、荷重的增大，引起建筑物發生沉降變形的可能風險也加大。在建造與運營過程中，沉降測量發揮主要監測與保障作用，減少安全隱患發生[1]。在建筑物沉降監測方法中，水準測量是最常規，使用最頻繁的方法[2]。文獻[3]～[6]均表明，到目前為止，利用精密電子儀器，采用水準測量技術，依據工程作業規范，對建筑物實施沉降監測是工程實踐中的普遍做法，被應用于不同類型的中高層建筑物的沉降監測。但由于受工程施工、外業觀測保障措施不到位以及數據優化處理方法欠佳等諸多因素的影響，導致數據信息精度與可信度較低。根據沉降測量高精度監測要求，觀測數據不能準確反映建筑物的沉降量實際情況。本文主要對現有水準測量數據平差處理中存在的不足，進行改進處理，提高沉降觀測數據的精度。

在水準網測量數據處理環節中，針對測量誤差，正確定權是參數估計的重要一步。一般做法，依靠水準路線長度、測站數以及定權數學模型。實踐中發現，不同定權方法對估計結果影響很大，結果之間存在較大差異性。文獻[7]以實例說明，水準控制網的觀測數據按照測段距離與按測站數定權平差存在差異。且對建筑沉降觀測而言，按照測段距離定權平差并不合適，而按照測站數定權平差計算，既有失權比之間的準確性，又嚴重影響參數估值的精確性。針對此問題，本文摒棄定權的常規思維，另辟蹊徑，從水準網誤差方程出發，對路線長度與高程兩變量之間的函數關系重新研究。嘗試基于微分思想與中值定理，建立水準網線性混合效應模型，使用最小二乘法統一理論進行參數估計。經過模擬試驗以及工程案例分析，結果表明，水準網利用線性混合效應模型進行平差計算較傳統間接平差具有無需定權、參數估計精度高、沉降趨勢特征明顯等優勢，為其應用與推廣奠定理論基礎。

1 模型建立與參數估計

1.1 模型建立

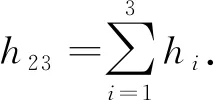
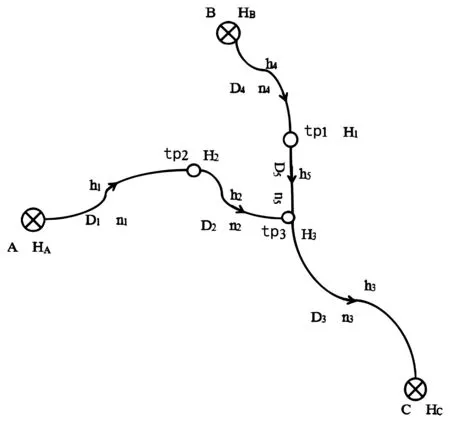
圖1a 水準網示意圖

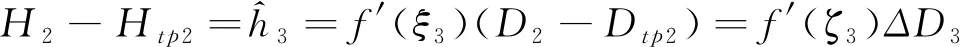
(1)

依照微分中值定理的幾何意義可知，f′(ζ1)為切線斜率，如圖1b所示，ζ1處切線e′f′與直線mn平行。但若測量數據含有誤差，導致切斜e′f′有θ1角偏轉，切線e′f′旋轉到ef處。記直線ef傾斜角α1，則改正后切線e′f′傾斜角α1-θ1，斜率tan(α1-θ1)。則利用三角函數和差角公式與泰勒公式，可得(2)式。

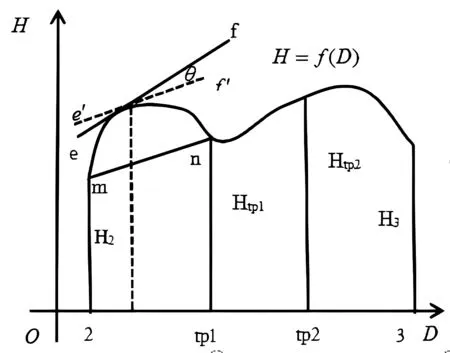
圖1b 水準網測段D-H函數關系

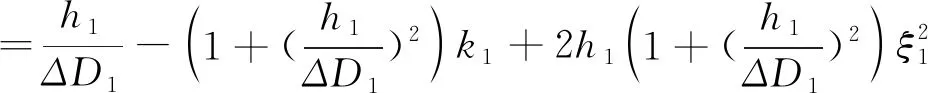
(2)

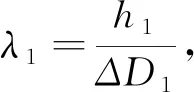
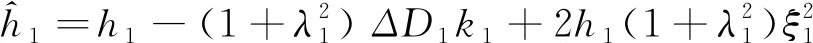
(3)

同理。第二、三測站改正高差

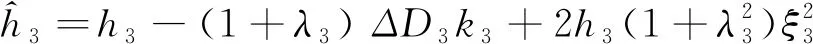
(4)

將第一、二、三個測站高差求和，則測段2-3的改正高差

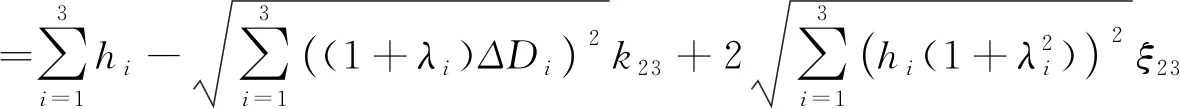
(5)

(6)

寫出水準網所有測段A-2、2-3、B-1、1-3、3-C的改正高差

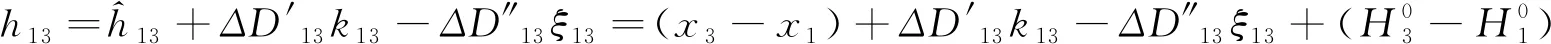
(7)

寫成矩陣形式：

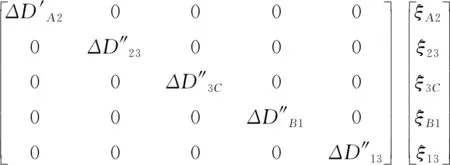
(8)

從而，概括水準網線性混合效應模型，可用(9)表示：

y=Ax+Bk+Cε

(9)

其中，y為觀測量Y與待定高程近似值的差值，x為固定效應，k、ε為隨機效應，假定滿足正態分布，均值E(k)=0，E(ξ)=E(k2)≈σ2[1,1,…,1]T，σ2一般是10-6左右(參照模擬算例)，可近似看成0，E(y)=Ax.k、ε具有相關性，聯合方差

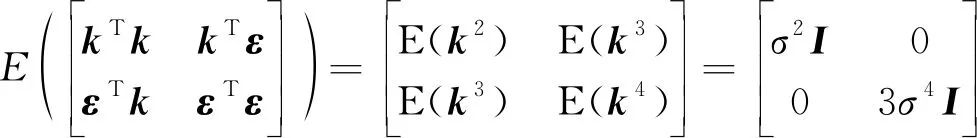
(10)

即

(11)

1.2 待定點高程估值與w權重的確定

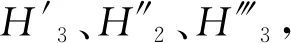
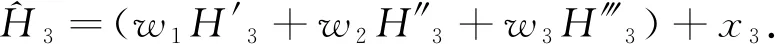
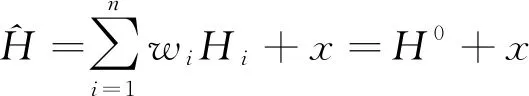
(12)

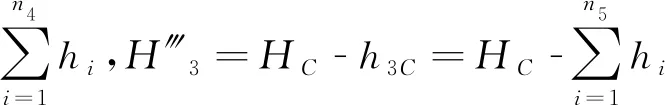
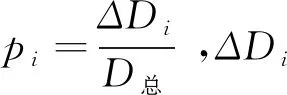
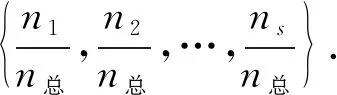
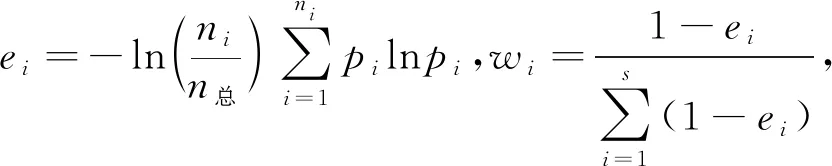
(13)

1.3 參數估計

1.3.1 固定效應的最小二乘估計 對于水準網線性混合模型y=Ax+Bk+Cξ，令V=y-Ax=Bk+Cξ，V～N(0,∑),則

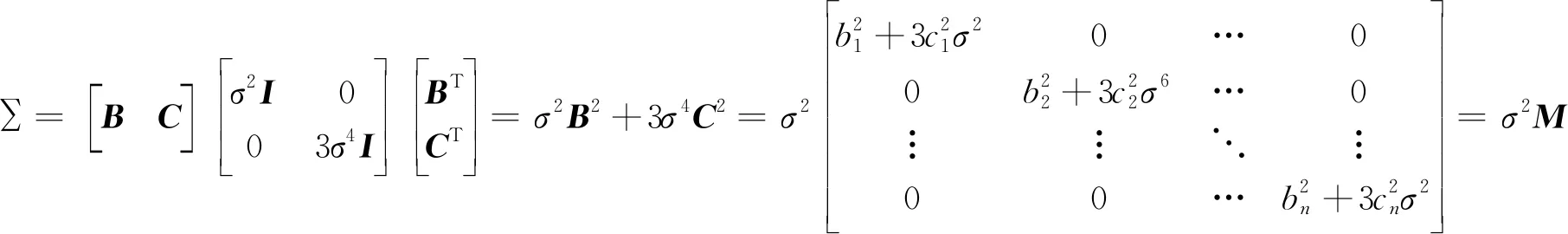
(14)

一般情況下，M是正定矩陣[9]，即

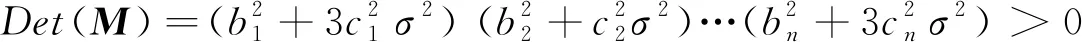
(15)

依據最小二乘法統一理論，可構造Q(x,σ)函數，

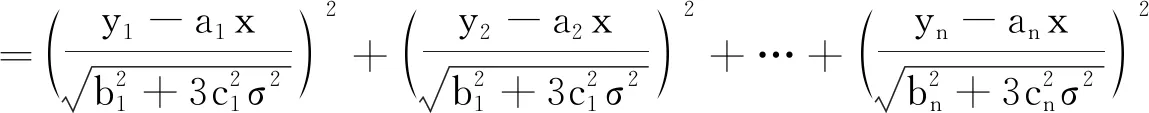
(16)

進行如下線性變換

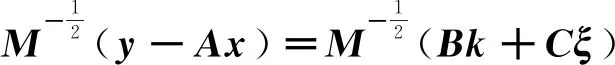
(17)

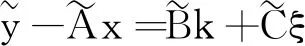
(18)

根據普通最小二乘法原理，得到LS解

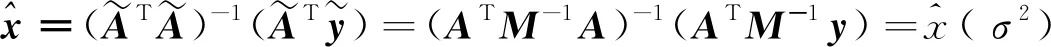
(19)

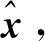
所以

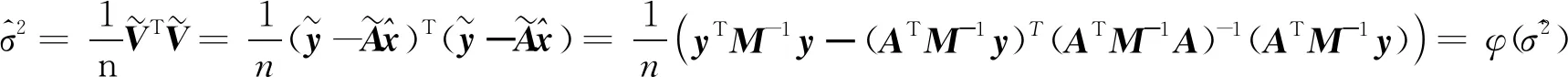
(20)

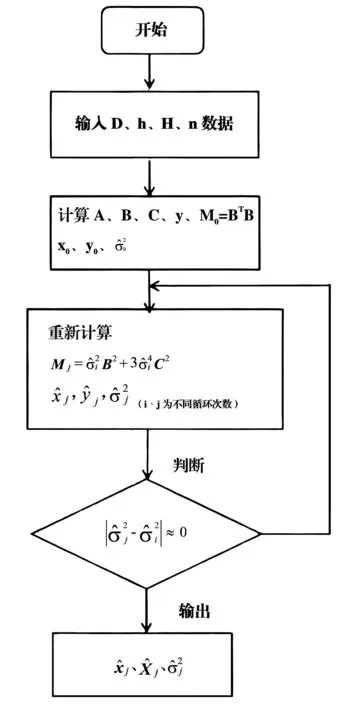
圖估計算法流程圖

2 模擬試驗

為檢驗水準網混合效應模型的平差計算有效性與優勢，本文模擬實際施工現場，在室內進行試驗，將試驗結果與傳統算法進行比較。試驗設計過程如下：

1)采用某沉降監測工程中某條單一閉合水準路線，除觀測高差h以外其他數據不變，包括起算數據HA、測站數ni與測站視距Di(i=1,2,…,50)，具體數據如表1.

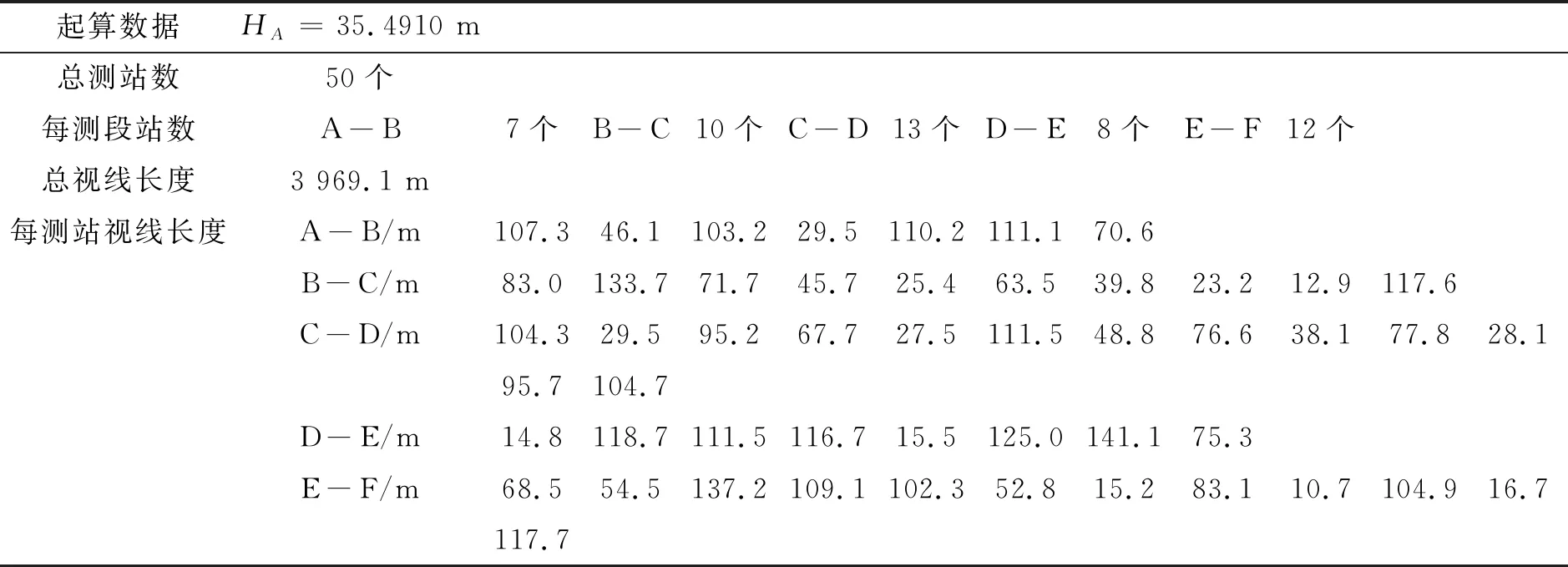
表1 模擬試驗起算數據與其他數據

2)利用函數H=HA+A*sin(2π*Di/D總)，A=0.003(D總為水準路線總長)插入50個高程點，計算出每個點的高程真值Hi，包括模擬沉降觀測點HB=37.4979m、HC=37.6849m、HD=33.7414m、HE=32.0109m.利用相鄰兩點高程真值求得每測站高差真值hij=Hj-Hi(i≠j).

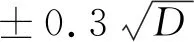
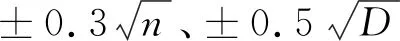
4)采用模擬觀測數據，建立線性混合效應數學模型，按照最小二乘算法對模型參數進行估計，結合參數值，計算出B、C、D、E四個點高程估計值。

5)B、C、D、E四個點高程估計值與真值比較，算出之間的不符值VB、VC、VD、VE，

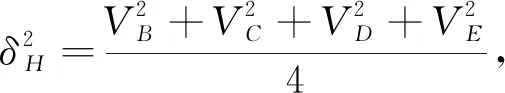
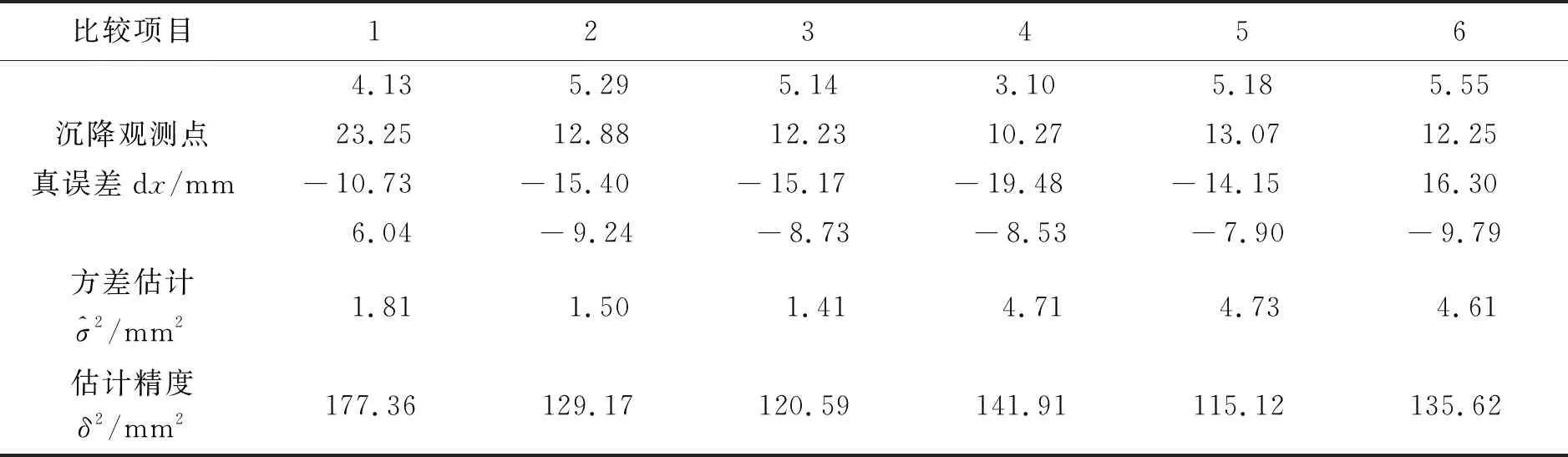
表2 試驗結果比較(間接平差)

從表2與表3、圖3(為突出數據差異性與數字表示清晰，圖3a數據擴大1 000倍，取一位小數)對比可看出，水準網采用線性混合效應模型平差計算，結果更優。第一，殘差方差估計值更小。傳統算法的方差估值處于1.41～4.73 mm2之間,而線性混合效應模型則在0.05(10-6)～7.45(10-6) mm2之間。第二，在同一種觀測條件下，線性混合效應模型平差結果相比較真值，誤差更小，估值精度高，即沉降觀測點的高程估值更接近真實值。比如在編號6的觀測條件下，線性混合效應模型估計精度為2.22 mm2，而傳統算法為115.12 mm2.第三，在非相同觀測條件下，觀測精度越高，線性混合效應模型的估計精度越高，優勢越明顯。比如，編號4比編號5的估計精度多了6.66 mm2.第四、傳統平差方法平差結果受距離或測站定權的因素影響，估計精度表現出差異性。而線性混合效應模型無需定權，完全避免這種因素影響，估值只與外業觀測條件有關。總之，對于精密水準測量(尤其沉降觀測工作)來說，采用線性混合效應模型進行平差計算更為合適。

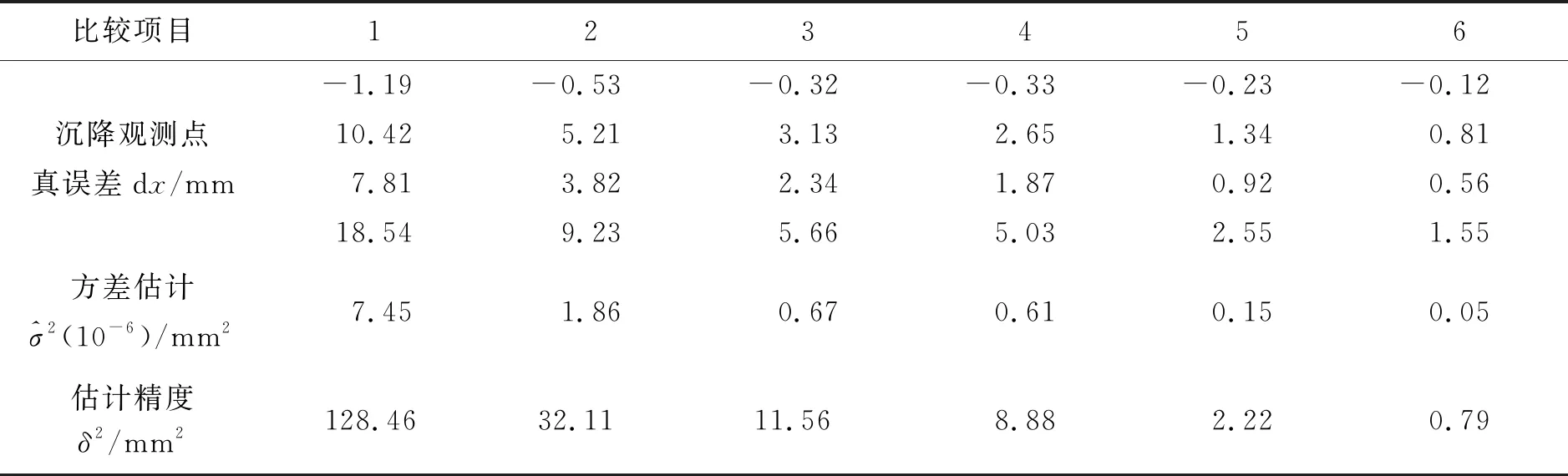
表3 試驗結果(線性混合效應模型)

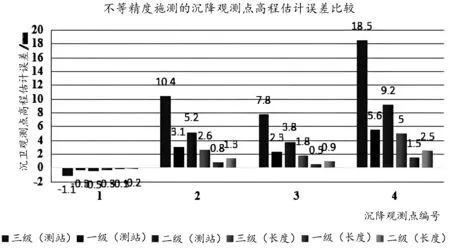
圖3a 參數估計真誤差對比

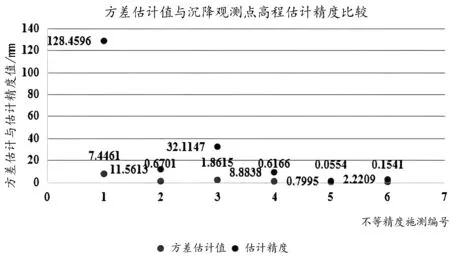
圖3b 殘差方差估計與參數估計精度對比

3 建筑物沉降觀測數據處理與分析

3.1 工程概況與施測工作

該建筑物位于新疆地區某路人群密集地段，占地5萬平方米，建筑面積8 453平方米，為地上6層、鋼筋混凝土框架結構。因管線跑水造成地基下沉，建筑物中部以及西部墻體多處出現裂縫。現需通過監測建筑物底部各結構點的沉降量、沉降差值及沉降速度，預測沉降發展趨勢。根據現場實際情況與規范要求，5個基準點均布設在建筑物的沉降區域之外的安全地點。監測點的埋設采用深埋加基礎底盤現澆的方法，深度約為15～20 cm.根據建筑物特點，在其上共布設18個觀測點(編號從J1～J18)，均布設在距離地面0.5 m高左右的墻柱上。基準點與觀測點分布情況詳見圖4.

圖4 基準點及沉降觀測點布置圖

監測網按照一等水準規范要求施測，5個監測點組成一條閉合的環形線路，基準0點為起始高程點，H0=835.3705 m.沉降觀測點的施測組成環形線路，按規范二等水準技術要求進行施測。15天一周期，共測40 個周期，測量成果各項限差均符合技術要求。

3.2 數據處理方法與結果對比分析

每期數據都采用間接平差與線性混合效應模型進行平差處理，求得每期J1～J18沉降觀測點的高程估值。根據相鄰兩期高程估值的變化，計算沉降量、累計沉降量、沉降速率等數值，依據數據繪出累計沉降量圖(圖5a)、沉降累積量與時間關系圖(圖5b)、沉降觀測點速率變化圖(圖6)。通過對圖5b觀察，發現沉降觀測點表現出明顯直線下降趨勢，于是對沉降累積量最大的J11點，通過一元線性回歸方程進行擬合，求出沉降預測方程。

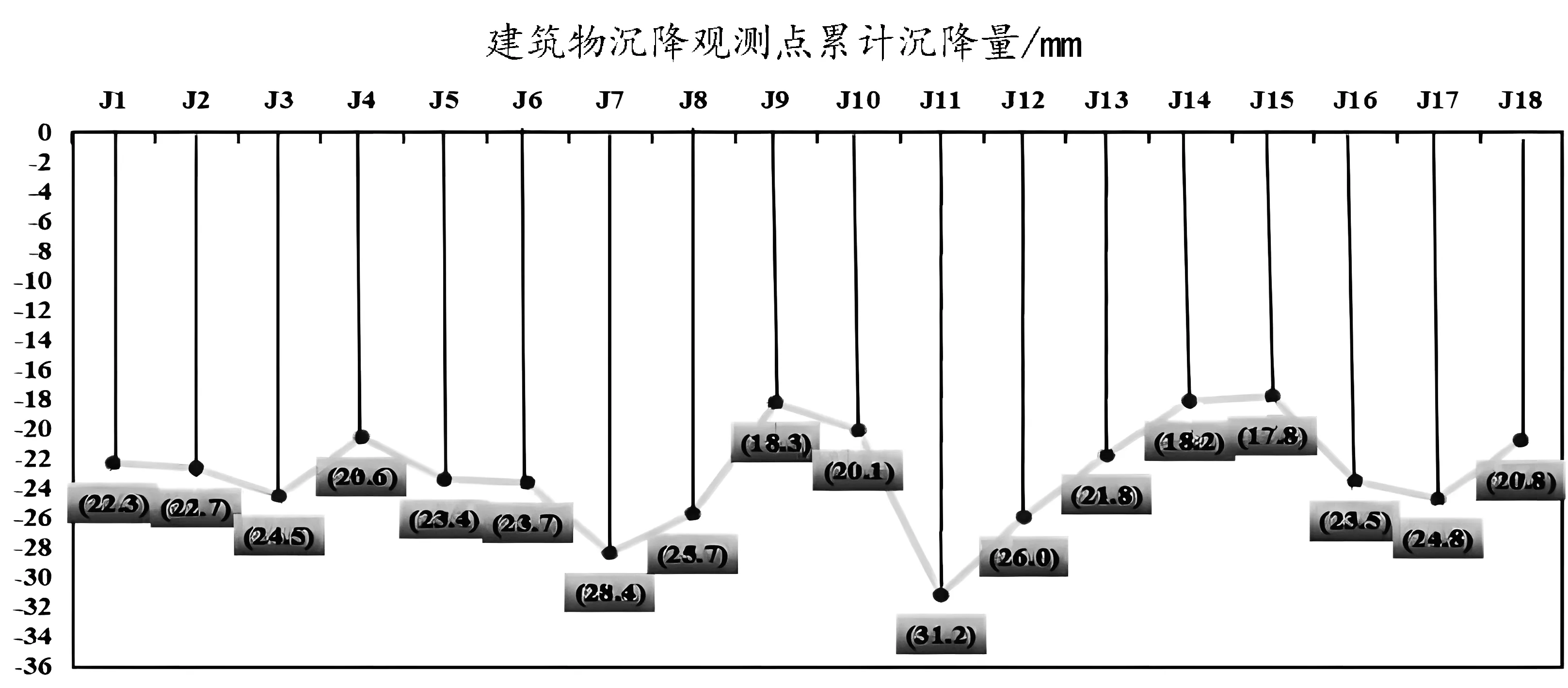
間接平差模型

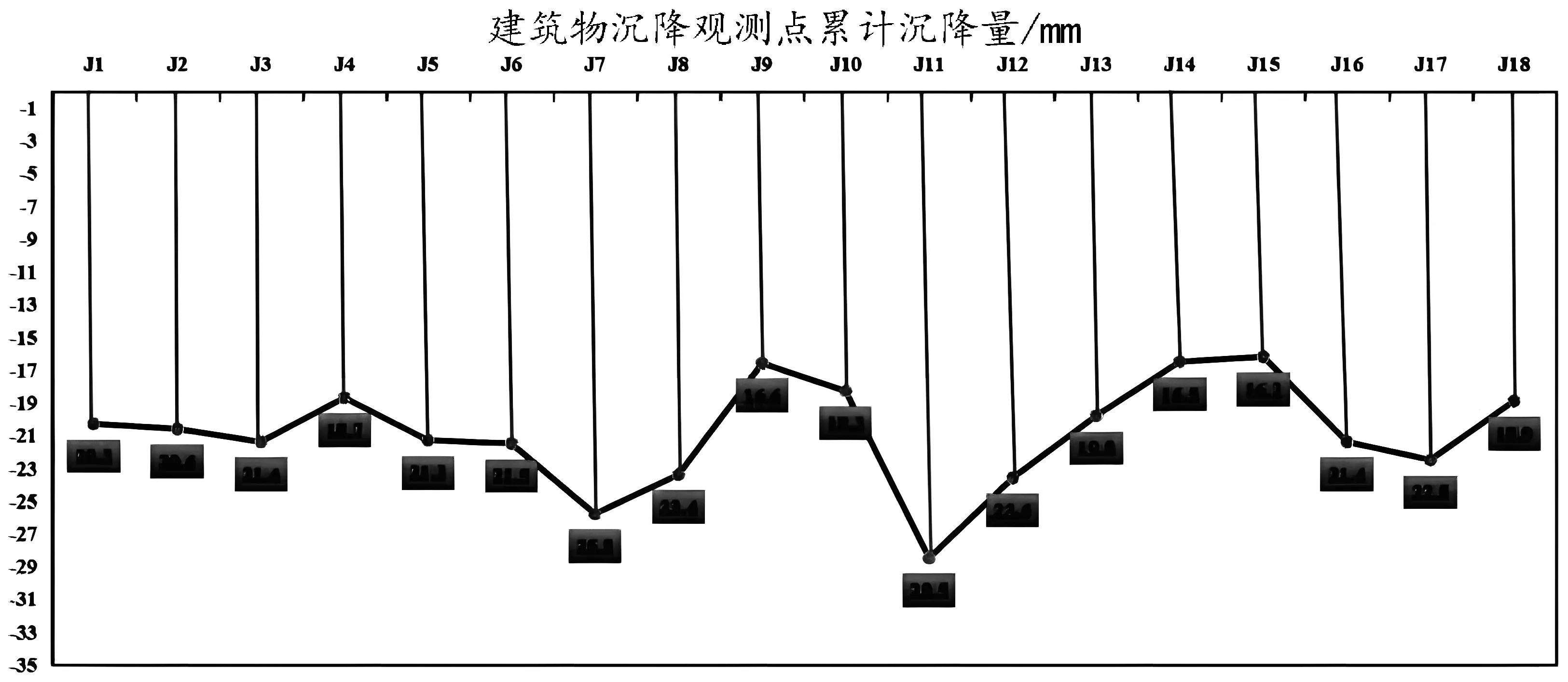
線性混合效應模型

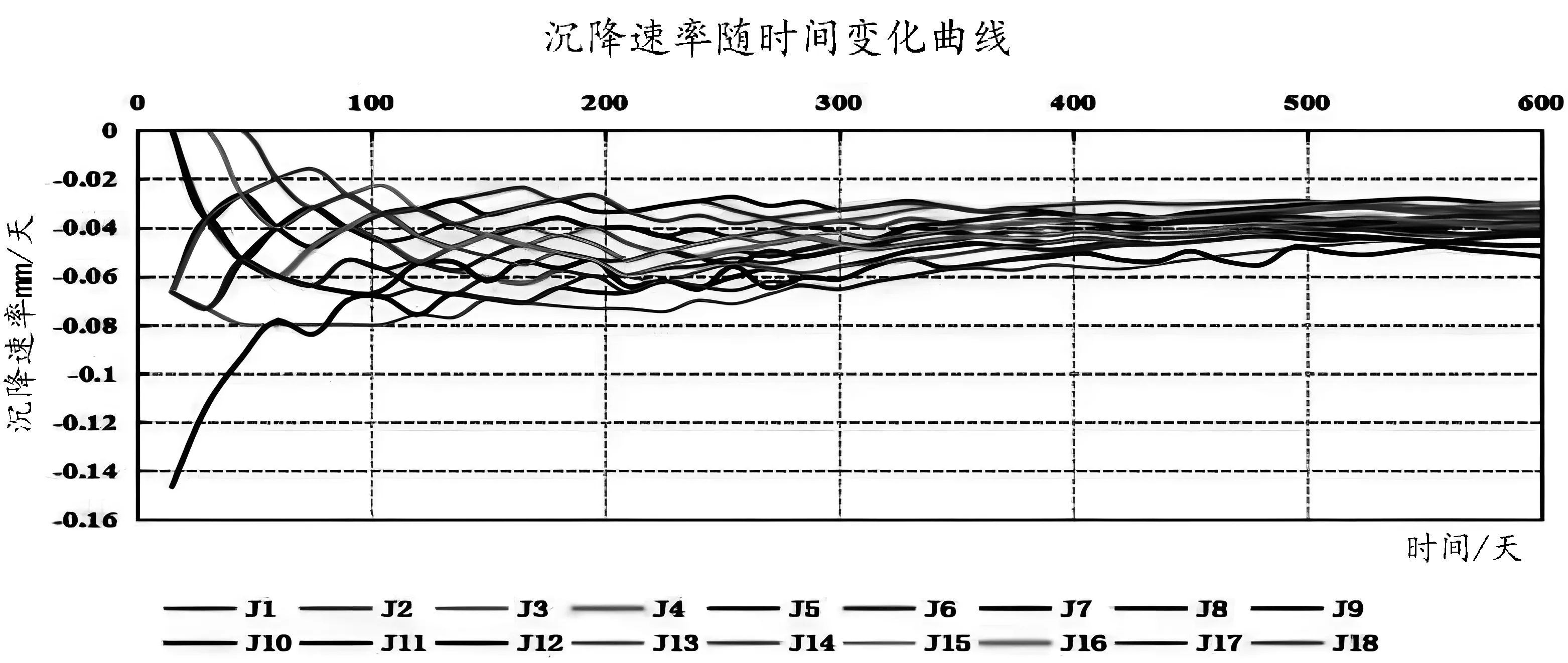
圖6 沉降點速率變化(間接平差模型(左)/線性混合效應模型(右))

從圖5、圖6、圖7比較可以看出，采用上述兩種方法平差計算，1)沉降觀測點高程估計存在一定的差異性，而且這種差異會引起沉降量、沉降累積量、沉降速率等計算量的不同。2)與傳統算法相比較，通過線性混合效應模型計算的沉降觀測點高程估值以及用估值計算的沉降量、累計沉降量與沉降速率，受誤差影響較小，沉降趨勢特征明顯。3)通過兩種方法計算的觀測高程估值，雖然存在一定程度的差異，但不影響建筑物下降趨勢特征的判斷。但是會影響到預測方程以及預測結果，比如，預計J11點在615天的累計沉降量，傳統算法結果為31.18 mm，新算法為28.87 mm，之間有2.31 mm的差別。這點差別不容小覷，因為時間越長，這種差別更大，最終會影響建筑物倒塌臨界點的判斷，應予重視。

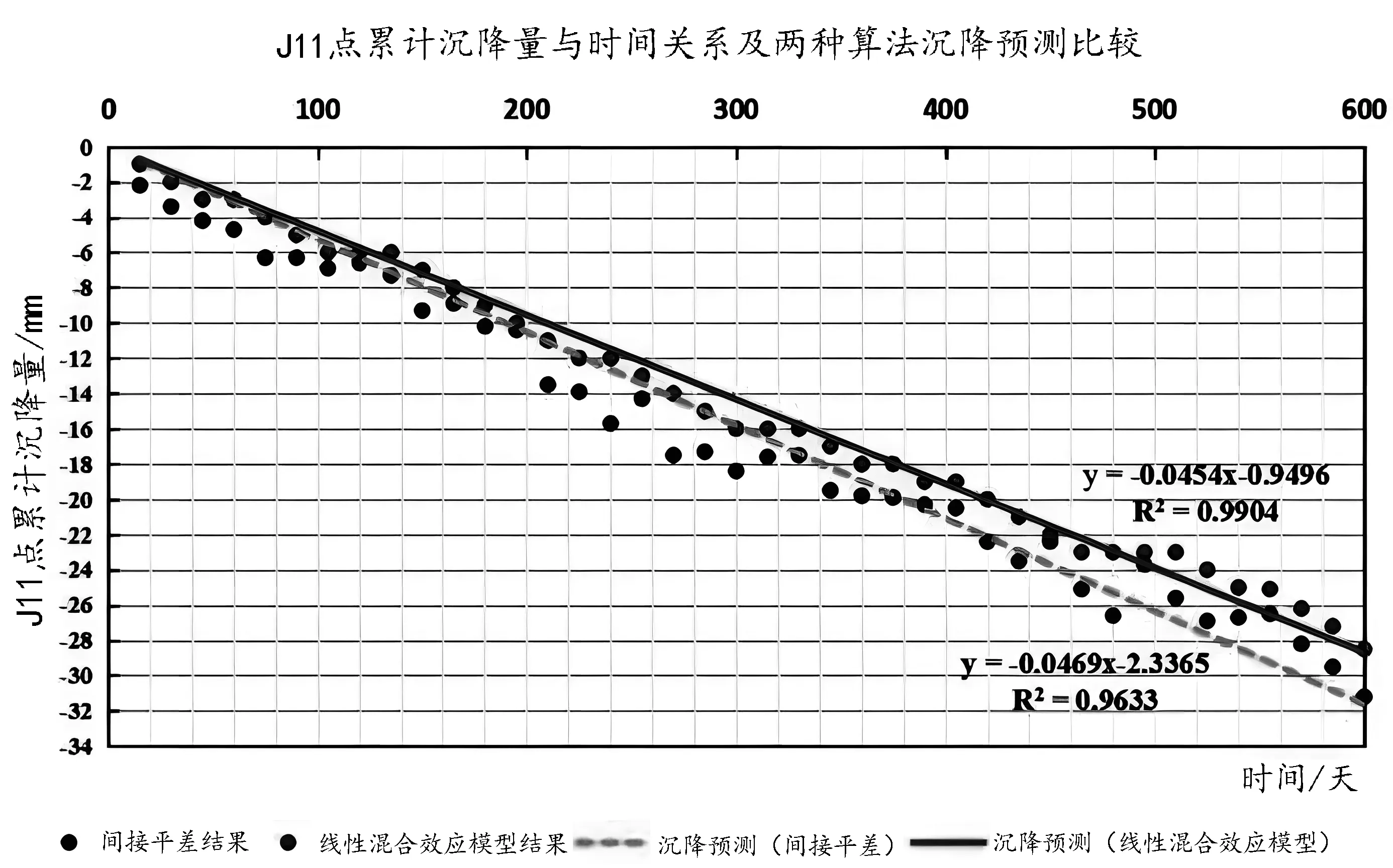
圖7 兩種方法沉降預測差異對比

4 結束語

本文提出的線性混合效應模型以及參數的確定方法為水準網平差計算增加了一條新的途徑。本文通過模擬試驗以及沉降監測數據處理與分析表明，水準網線性混合效應模型較傳統間接平差模型具有無需定權、參數估計精度高、沉降趨勢特征明顯等優勢。另外，二維、三維空間是否也存在線性混合效應模型，有待進一步探討與研究[11,12]。