基于能量距離法的多維分類變量的分布差異檢驗
彭東海,張留偉
(1.中山職業技術學院數學教研室,廣東 中山 528404;2.中山大學測繪學院,廣東 珠海 519082)
0 引言
分類數據又稱定性數據,它是反映對象的屬性特征,是非量化的數據。例如,社會調查數據中的性別、職業、學歷、婚姻狀況等;醫學研究數據中病人的血型、吸煙與否、采取的治療方案的類別、檢測結果的陽性與陰性等。可見,分類數據是我們實際生活中廣泛存在的一類數據類型,因而比較兩組分類數據的分布差異也就成了我們經常遇到的問題。例如,比較兩個不同行業從業人員的學歷結構差異,或比較不同性別職業分布差異等。這類問題概括來說,就是要比較兩個獨立的分類變量的分布差異,用數學語言表述如下:
假設X與Y是兩個獨立的離散型隨機變量,概率分布列分別為:
P(X=ai)=pi,i=1,2,…,r,
與
P(Y=ai)=qi,i=1,2,…,r.
其中,pi≥0,qi≥0, ∑ipi=1,∑iqi=1.它們對應的分布函數分別為F與G,考慮檢驗問題:
H0∶F=G
(1)
即
H0∶pi=qi,?i=1,2,…,r.
(2)
假設X1,X2,…,Xm是來自X的簡單隨機樣本,Y1,Y2,…,Yn是來自Y的簡單隨機樣本。對各樣本進行匯總后,可得頻數分布如表1、2:

表1 X的樣本頻數分布表
檢驗問題(1)的經典方法為卡方檢驗,卡方檢驗將X的樣本X1,X2,…,Xm與Y的樣本Y1,Y2,…,Yn進行合并,并對每個樣本添加標簽,標注它是來自X的樣本還是來自Y的樣本。因此,檢驗X與Y是否同分布等價于檢驗標簽變量與分類值是否相互獨立,從而,我們可將表1的X的樣本頻數分布表與表2的Y的樣本頻數分布表合并成一個新的如表3所示的列聯表:

表2 Y的樣本頻數分布表

表3 X與Y的樣本的頻數列聯表
基于此表,可構造卡方檢驗統計量:

眾所周知,卡方檢驗僅適用于大樣本情形,它要求列聯表中小于5的理論次數不能多于20%.因此,當X與Y取值的類別比較多,而樣本量又不夠大時,容易出現列聯表中很多單元格頻數小于5,甚至為0.此時,如果我們仍采用卡方檢驗來檢驗兩個分布的差異,則可能會得到錯誤的結論。在此情形下,可參考文獻[1]關于卡方檢驗的一些傳統的修正方法。
能量距離 (Energy distance,ED)的概念由Székely 與Rizzo 在文獻 [2]中提出,它是由兩個獨立隨機向量的特征函數之差的模構造的,在選取一個特殊的權重函數進行積分之后,它可以表示成距離函數的期望形式。ED等于0當且僅當兩個分布相同,因此,ED是度量兩個獨立隨機向量分布差異的一個很好的測度。而樣本的ED只涉及兩點之間的距離的計算,它可以用來檢驗兩個獨立樣本是否同分布,它檢驗的對象可以是任意有限維數的隨機向量,只須滿足有限一階矩的條件即可,并且檢驗方法具有一致性。Székely 與Rizzo 在文獻[3~8]中分別展示了將ED用于處理諸如獨立樣本同分檢驗、單樣本分布檢驗、聚類分析等一系列經典統計問題的結果。這些研究結果表明,相比傳統的方法,ED方法計算簡便、適用于更廣泛分布類型的數據,且能處理多變量情況。近年來,ED方法引起了國內不少學者的關注。文獻[9]討論了基于ED推廣的Ward聚類算法研究,文獻[10]對ED做了幾點補充討論,文獻[11]則將ED用于二維列聯表的獨立性檢驗問題中,得到了一個比傳統卡方檢驗計算更簡便、在小樣本情形下具有更功效的檢驗統計量。
本文受文獻[1]啟發,基于獨立變量的ED概念,通過引入虛擬向量的方式,給出了兩個分類變量的ED的總體形式與樣本估計,基于該樣本估計,我們得到了一種新的檢驗方法,并采用置換程序計算該方法的檢驗p值。數值模擬顯示,相比傳統的卡方檢驗法,我們的方法不受列聯表中單元格的頻數影響,因此,大部分時候具有更高的功效。最后,我們將方法應用于一份涉及兩個多維分類向量的分布差異檢驗的數據中。
1 能量距離(ED)方法簡介
我們先回顧一下文獻[1]提出的兩個獨立的隨機變量的能量距離(ED)的定義及主要結果。
定義1[1]設X、Y為取值于d的兩個獨立的隨機向量,并且E|X|+E|Y|<∞,則X與Y的能量距離(ED)定義為:
ε(X,Y)∶=2E|X-Y|-E|X-X′|-E|Y-Y′|
其中|.|表示歐氏距離,X′是與X獨立同分布的隨機變量,Y′是與Y獨立同分布的隨機變量。

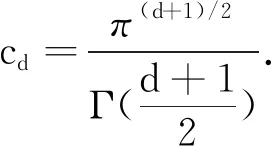
假設X1,X2,…,Xm是來自X的簡單隨機樣本,Y1,Y2,…,Yn是來自Y的簡單隨機樣本,則ε(X,Y)的樣本估計為

(7)
文獻[1]證明了εm,n(X,Y)如下的大樣本性質:

定理2[1]設X與Y為取值于d的兩個獨立的隨機變量,X,Y分別有分布函數F,G,且E|X|+E|Y|<∞.則當X與Y的分布相同時,有

(8)


步驟1:由原始樣本{X1,X2,…,Xm}和{Y1,Y2,…,Yn}計算檢驗統計量Tm,n;
步驟2:對聯合樣本{Z1,Z2,…,Zm,Zm+1,…,Zm+n}={X1,X2,…,Xm,Y1,Y2,…,Yn}隨機地重新排列得
{Zπ(1),Zπ(2),…,Zπ(m),Zπ(m+1),…,Zπ(m+n)}
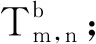


(9)
2 分類變量的能量距離
定義1中給出的能量距離的概念針對的兩個隨機向量X、Y要求為數值型變量,若X與Y為分類變量(向量),我們無法直接用(8)式給出的Tm,n統計量來檢驗X與Y的分布差異。為此,我們首先對X與Y構造相應的虛擬變量,將X與Y的分布差異檢驗問題等價地轉換成對兩個虛擬向量的分布差異的檢驗。具體地,記ei,i=1,2,…,r為r空間中第i個分量元素為1,其他位置元素均為0的單位向量,引入虛擬向量eX與eY如下:
eX=ei,若X=ai,i=1,2,…,r,
及
eY=ei,若Y=ai,i=1,2,…,r.
顯然,P(eX=ei)=P(X=ai)=pi及P(eY=ei)=P(Y=ai)=qi,i=1,2,…,r.因此,檢驗X與Y是否同分布等價于檢驗eX與eY是否同分布。即我們將分類變量X與Y的分布差異檢驗問題等價地轉換成了Rr空間中兩個隨機向量的eX與eY的分布差異的檢驗問題。此時,eX與eY的能量距離有表達式:
ε(eX,eY)=2E|eX-eY|-E|eX-eX′|-E|eY-eY′|
其中,eX′是與eX獨立同分布的隨機向量,eY′是與eY獨立同分布的隨機向量。ε(eX,eY)的樣本估計相應為:

3 數值模擬
在這一節中,我們利用R軟件通過幾個簡單的模擬實驗來比較本文提出的方法與傳統的卡方檢驗的表現。考慮以下6個例子:

例3:X與Y獨立,均以q,q2,…,qr-1, 1-(q+q2+…+qr-1) 的概率分別取a1,a2,…,ar,其中
q=1/2;

1-(q+q2+…+qr-1)的概率分別取a1,a2,…,ar,其中q=1/2;

顯然,上面例子中,例1至例3為X與Y同分布的情形,而例4至例6為X與Y不同分類的情形。類別個數考慮r=3, 5, 10, 20, 40五種情況,設定顯著性水平α=0.05,Tm,n通過499次置換計算p值,樣本容量考慮:1)m=30,n=50; 2)m=50,n=80; 3)m=80,n=100; 4)m=100,n=100; 5)m=100,n=150五種情況。所有的模擬都通過1 000次重復試驗來近似相應的第一類錯誤與功效。表4給出了各種情形下卡方檢驗與Tm,n的模擬結果。
從表4中我們可以看到,對于例1至例3,Tm,n在各種情形下都能將第一類錯誤很好地控制在名義水平0.05附近,而卡方檢驗在r=20與r=40的情形下,當樣本量較小(如m=30,n=50與m=50,n=80)的時候,第一類錯誤遠小于名義水平0.05.這是因為,當分類的類別個數較多,而樣本量較小時,列聯表中可能會出現很多單元格的期望頻數小于5,從而導致卡方檢驗統計量近似卡方分布的效果不好,因此第一類錯誤不準確。很明顯,在樣本量增大的過程中,這種情況稍微得到了改善,卡方檢驗的第一類錯誤逐漸靠近名義水平。對于例4至例6,在類別個數r≤10,且樣本量較大(如m=80,n=100及以上)時,大部分時候卡方檢驗的功效稍微高于Tm,n,但在樣本量較小(如m=30,n=50)時,或類別個數較多(如r=40)時,卡方檢驗的功效均不如Tm,n.總的來說,我們的方法Tm,n在小樣本或類別個數較多時相比卡方檢驗更有優勢。

表4 6個例子在不同樣本容量下卡方檢驗與Tm,n檢驗法的第一類錯誤與功效比較(α=0.05)
4 實例分析
本小節中,我們利用本文提出的方法來分析一份實際數據。數據來源于R軟件的MASS包中的birthwt數據集,該數據集記錄了1986年在馬薩諸塞州斯普林菲爾德的Baystate醫療中心產婦與新生兒的信息,共189條觀測與10個變量。各變量的意義及取值如表5所示。
我們提取其中的race、smoke、ht、ui、ftv這5個分類變量與離散變量來做分析,看看低體重產兒(low=0)的母親與正常產兒(low=1)的母親的這些指標之間是否存在差異。下面的圖1至圖5分別給出了兩組產婦之間的這5個指標的分布差異對比圖。從這些圖中,我們可以看到,低體重產兒的產婦與正常產兒的產婦之間的這些指標的分布有明顯的差異。比如,相比正常產兒的母親,低產兒母親中黑人比例、吸煙比例、有高血壓史的比例、存在子宮刺激的比例以及在懷孕前三個月未看過醫生的比例都偏高。下面我們采用本文提出的方法與經典的卡方檢驗來檢驗兩組樣本的這5個分類變量的聯合分布的差異。

表5 birthwt數據集中各變量名稱及其意義與取值
顯然,兩組的race、smoke、ht、ui與ftv這5個變量的聯合分布都是取值在3×2×2×2×7=168個類別上的離散分布,理論上的聯合列聯表為2×168的二維表,但由于單元格中大部分元素為0,去掉整行或整列為0的行或列后,只剩下2×46的列聯表。此時,我們采用卡方檢驗對此列聯表做獨立性檢驗,可得卡方統計量的值為54.688, 相應的p值為0.1527.這說明,卡方檢驗結果顯示,低體重產兒的產婦與正常產兒的產婦之間的這5個分類指標的聯合分布沒有明顯的差異。接下來,我們采用本文提出的Tm,n重新對兩組的5個分類指標的聯合分布做差異性檢驗,可得統計量的值為 28 447.99,在499次置換樣本的情況下,得到相應的p值為0.024.因此,我們的方法說明,低體重產兒的產婦與正常產兒的產婦之間的這5個分類指標的聯合分布是有明顯的差異的,這跟圖1至圖5展示的結果是一致的。

圖1 低體重產兒與正常產兒的產婦的種族分布對比圖

圖2 低體重產兒與正常產兒的產婦是否吸煙的分布對比圖


圖5 低體重產兒與正常產兒的產婦是在懷孕前三個月看醫生次數的分布對比圖
5 總結
本文基于獨立隨機向量的能量距離(ED)的概念給出了分類變量(向量)的能量距離(ED)的定義,由此給出了一種新的檢驗兩個分類變量(向量)的分布差異的檢驗統計量。該檢驗方法的檢驗統計量只涉及兩組樣本頻數的差距,因此計算非常簡便,且適用于任意有限維的分類的隨機向量。數值模擬結果說明,在小樣本或類別變量較多的情形下,該方法比經典的卡方檢驗法能更好地控制第一類錯誤,同時具有更高的功效。

