基于多環拼裝模型的盾構管片非線性承載性能及加固效應研究

成全，王 震，丁 智

(1. 浙江交通職業技術學院, 浙江 杭州 311112；2. 浙大城市學院，浙江 杭州 310015；3. 浙江省城市盾構隧道安全建造與智能養護重點實驗室, 浙江 杭州 310015)

0 引言

襯砌管片結構廣泛應用于城市地下盾構隧道工程領域[1-2]。作為隧道外部圍護支撐結構體系，襯砌管片在外部圍壓作用下的力學承載性能及破壞模式對于隧道的整體安全保障至關重要[3-5]。

國內外對于隧道盾構管片的力學承載性能及破壞模式已有一些相關研究[6-9]。王士民等[6]采用相似模型試驗，對不同拼裝方式下襯砌管片的受力承載性能和破壞特征規律進行了研究，表明通縫拼裝比錯縫拼裝的整體剛度小。汪亦顯等[7]采用局部剛度折減和接頭張合相結合的力學模型，對管片接頭連接螺栓的內力和變形分布規律進行了研究。楊文波等[8]對列車振動荷載作用下，管片接縫對襯砌管片結構及周圍土層動力響應進行了數值模擬和模型試驗研究，表明接縫對管片環所受軸力有明顯影響。

然而，這些研究主要集中于襯砌管片在圍壓作用下的內力和變形特性、接頭剛度和錯縫拼接方式及其影響等。當在某些極端條件工況下，襯砌管片由于整體結構的過大變形及失穩破壞往往也會成為影響其使用和承載的重要因素[10]。因而，按概率極限狀態方法進行管片整體結構性能設計，并考慮其在極端工況條件下的非線性極限穩定承載性能就顯得尤為重要。國內外關于這方面的相關研究文獻相對較少[10-11]。朱瑤宏等[11]采用足尺模型試驗，對通用環拼裝襯砌管片的極限承載能力和破壞機理進行了研究，表明荷載-位移曲線呈彈塑性變化。

襯砌管片由于破損等缺陷往往需要進行后期加固處理，目前主要采用粘貼纖維布加固法[12-13]和鋼板襯加固法[14-15]。然而，前者對于管片側部受彎區加固效果差，后者重量大且易腐蝕。高性能復合砂漿鋼筋網加固法(HPF法)是一種應用較廣的混凝土加固方法，目前國內外學者對其加固性能已有較多研究[16-17]。然而將其應用于隧道領域并不多見，至于該加固方式對管片極限承載的性能影響則尚無相關文獻，有必要進行深入的研究。

本研究針對盾構隧道管片襯砌結構，首先給出了基于殼-彈簧模擬和外部圍壓加載模式的計算理論；接著建立了15環精細管片結構三維有限元模型，并對正常使用工況下管片的應力和變形分布規律進行了分析；然后針對極端荷載工況下，對管片的線性屈曲模態和非線性極限穩定承載性能進行了研究；最后分別考慮全部環加固和間隔環加固2種方式，針對高性能復合砂漿鋼筋網加固對襯砌管片極限承載性能的影響進行初步探討。

值得指出的是，以往研究中一般采用單環或三環模型進行承載和加固分析[15]，而無法考慮實際為多環情況下的整體效應，本研究采用15環的殼-彈簧精細化管片結構模型進行研究，充分考慮了接頭彈簧、接地彈簧以及非線性材料因素，分析結果更具準確性，也是本研究與以往研究最大的不同，對管片實際施工具有一定的工程指導意義。

1 計算理論

1.1 結構模型

襯砌管片結構是由一系列弧形管片單體通過環向、縱向螺栓拼接而成的隧道外圍護多環支撐結構。為真實模擬襯砌管片在外部圍壓作用下的力學承載性能，采用15環精細管片結構模型進行分析，各相鄰單環之間為錯縫拼接形式，見圖1。

圖1 15環精細管片結構模型Fig.1 Refined 15-ring segment structure model

采用殼-彈簧模型進行模擬，其中管片為殼單元，管片環向接頭、縱向接頭為轉動彈簧單元，見圖2。環向、縱向接頭彈簧單元分別沿管片縱縫、環縫布置在重合節點對上。土體抗力采用僅受壓的雙向接地彈簧單元模擬，假定土體抗力彈簧單元沿管片為整環布置。

圖2 殼-彈簧模型和加載模式Fig.2 Shell-spring model and loading mode

襯砌管片為鋼筋混凝土材料，采用非線性的Hongnestad本構模型，應力-應變關系式如下：

(1)

式中，fc為峰值壓應力；ε0=0.002為對應峰值壓應力的壓應變；εu=0.003 3為極限壓應變。

1.2 圍壓荷載

襯砌管片外部圍壓荷載包括管片頂部土壓力p1，底部土壓力p2，側向土壓力(q1，q2)和土體抗力q，管片自重為G，其中側向土壓力為梯形分布，加載模式見圖2。

頂部土壓力p1由實際埋深土壓力和地面超載換算埋深土壓力組成，即：

p1=r1h0=r1(h1+p/r1)，

(2)

式中，p為地面超載；r1為土體平均重度；h1為頂部實際埋深；h0為頂部計算總埋深。

底部土壓力p2由頂部土壓力和管片自重換算壓力組成，即：

p2=p1+r2t，

(3)

式中，r2為管片重度；t為管片厚度。

側向土壓力根據埋深處土壓力與土體側壓力系數的乘積獲得，即頂部、底部埋深處側向土壓力q1，q2分別為：

(4)

式中，μ為土體側壓力系數；D1為管片外直徑。

土體抗力q采用m值法計算，假定土體抗力與土體變形為僅單向受壓的線性關系，即：

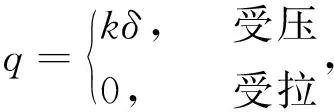
(5)

式中，k為土體抗力系數；δ為節點變形。

2 非線性有限元分析

2.1 有限元模型的建立

以長三角地區某地鐵隧道標準盾構襯砌管片結構為例，結構示意圖見圖3，管片結構承載相關的具體參數詳見表1。管片單環沿環向由1塊封頂塊、2塊鄰接塊和3塊標準塊組成，相鄰單環為錯縫拼裝；管片材料為混凝土，采用非線性Hongnestad本構模型；管片接頭采用線性轉動彈簧模擬，考慮長三角地區的中厚軟黏土。有限元分析模型見圖4。

圖4 有限元分析模型Fig.4 Finite element analysis model

表1 管片結構承載相關的參數Tab.1 Parameters related to bearing capacity of segment structure

圖3 標準襯砌管片結構Fig.3 Standard lining segment structure

2.2 應力和變形結果

在正常使用工況的外部圍壓加載下，圖5為襯砌管片的Von Mises應力分布云圖，圖6為襯砌管片的全位移分布云圖。由圖5和圖6可知，正常使用圍壓加載時，襯砌管片主要呈現為類似于扁橢圓的橫向整體變形形式，其中上、下側為向內凹進，左、右側為向外突出。這主要是由于土壓力一般要比側向土壓力大所導致的。

圖5 Von Mises應力分布云圖(單位：Pa，變形放大50倍)Fig.5 Nephograms of Von Mises stress distribution (unit: Pa, 50 times deformation magnification)

圖6 全位移分布云圖(單位：m，變形放大50倍)Fig.6 Nephograms of full displacement distribution (unit: m, 50 times deformation magnification)

由圖5可知，最大Mises應力出現在襯砌管片的左、右側中心附近區域和上、下側中心附近區域；最大Mises應力為13.5 MPa，約為單軸抗壓強度fc的0.585倍，因而襯砌管片具有較好的承載性能和安全余量。由于管片單體之間為轉動彈簧螺栓連接，可以明顯觀察到接縫附近區域的Mises應力分布具有不連續性，相鄰環的最大Mises應力位置并不一致，存在鋸齒狀分布。

由圖6可知，最大全位移出現在襯砌管片的左、右側中心附近區域和上、下側中心附近區域，最大位移為6.248 mm。在隧道結構中，管片橢圓度e是衡量其變形的一個重要指標，規范《盾構法隧道施工及驗收規范》(GB50446—2017)[18]中定義管片橢圓度e為：

e=2(a-b)/D1,

(6)

式中，a、b為橢圓長半軸長、短半軸長;D1為管片外直徑。

因而，管片最大位移對應的管片變形橢圓度e為4.03‰，小于6‰規范限值，符合正常使用要求。在接縫附近區域，相鄰環的最大位移分布也不完全一致，存在較小的鋸齒狀分布。

本研究采用基于非線性的Hongnestad本構模型進行分析，考慮了混凝土材料的非線性彈塑性效應，其應力應變結果更符合實際情況。

3 極限承載分析

管片結構的整體變形破壞(如橢圓度變形)是結構極限承載和變形的一個重要指標。本研究采用15環殼-彈簧精細化結構模型進行分析，主要是從整體角度上對管片的極限承載性能進行考察，具有較好的工程參考意義。值得指出的是，在進行整體分析時，出于計算量和計算效率的考慮，忽略了管片接頭壓碎、螺栓塑性破壞等局部破壞效應，關于局部破壞有待后續進一步深入研究。

3.1 線性屈曲分析

線性屈曲分析概念簡單，有利于初步掌握管片的整體穩定性能。取初始切線模量E0為彈性模量進行分析。表2為前10階線性屈曲荷載系數，圖7為前5階和第10階屈曲模態的變形模式。

表2 前10階線性極限荷載系數Tab.2 First 10-order linear ultimate load coefficients

圖7 屈曲模態變形Fig.7 Buckling mode deformation

由表2可知，襯砌管片的首階線性屈曲荷載系數為47.017，具有較好的穩定極限承載性能。由圖7可知，低階模態主要呈現為整體變形模式，高階模態開始出現多波形的局部屈曲變形模式。

3.2 非線性極限承載分析

非線性極限承載分析是通過跟蹤結構荷載-位移曲線以獲得平衡路徑，屬于極值點穩定問題，本節同時考慮材料、幾何雙重非線性進行非線性極限承載性能分析。材料非線性是指采用2.1節給出的非線性Hongnestad本構模型，幾何非線性是指計算時打開了有限元軟件的大變形開關。本研究主要考察了實際工程中出現較多的對稱圍壓荷載工況作用下，管片結構的極限承載性能。由第3.2節可知，管片頂部中心節點的豎向位移最大，因而文中均采用管片頂部中心節點的荷載-位移曲線進行非線性極限承載分析。根據結構屈曲特性，極限荷載一般取為荷載-位移曲線的收斂極值點或突變極值點。

圖8為襯砌管片頂部中心節點的荷載系數-豎向位移變化曲線。可知，荷載系數a隨著豎向位移u增大的變化趨勢為線性迅速增大、非線性平緩增大和趨于平緩收斂的變化過程。結構穩定的極限承載力取為收斂極值點的對應荷載，即有極限荷載系數a0為3.522，具有較好的非線性穩定承載性能。對應極限承載時的豎向位移為55.27 mm，對應管片變形橢圓度e為17.83‰。

圖8 荷載系數-豎向位移變化曲線Fig.8 Curve of load coefficient vs. vertical displacement

由于本研究所用精細化管片模型在以往研究中并未出現過，考慮將其極限承載時的豎向位移與文獻[19]中模型試驗位移(80～120 mm)進行間接對比，表明處于同一數量級，在一定程度上驗證了本研究模擬方法的合理性和有效性。

圖9為荷載系數的斜率變化-豎向位移變化曲線?？芍?，斜率變化隨著豎向位移u的增大逐漸減小，也即對應圖8中荷載系數a的變化趨于平緩并最終收斂的過程。

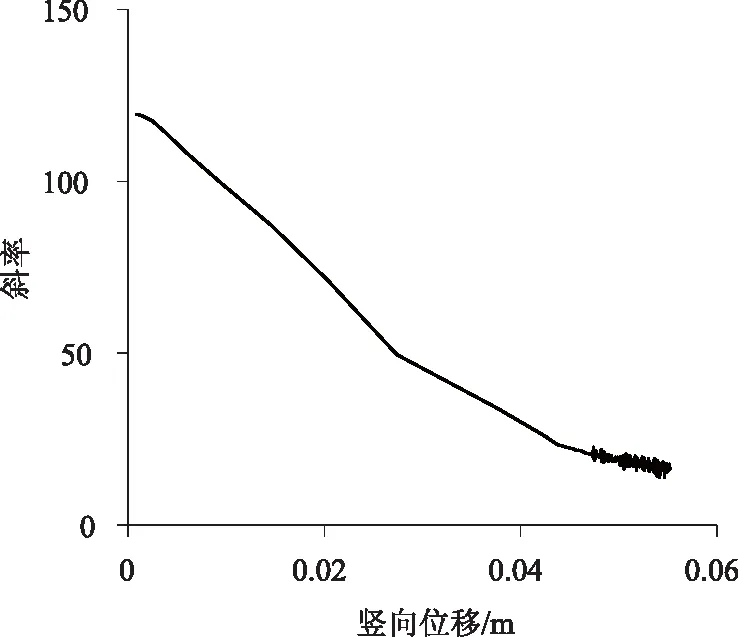
圖9 斜率-豎向位移變化曲線Fig.9 Curve of slope vs. vertical displacement

4 局部加固影響分析

高性能復合砂漿鋼筋網加固(HPF)是一種簡單高效的管片加固方式。本節僅為研究HPF加固后的管片極限承載性能，HPF加固區域按局部加厚的襯砌管片進行簡化處理。加固方式考慮間隔環加固和全部環加固兩種，加固層砂漿厚度為0.04 m，加固層寬度為0.8 m，每環居中內襯加固布置，結構模型見圖10。

圖10 襯砌管片加固模型Fig.10 Lining segment reinforcement models

有限元軟件中，對每個單環幅寬1.2 m范圍進行切割，劃分為中部區域(0.8 m)和兩側區域(0.2 m)；間隔環、全部環加固時，僅設置涉及加固環的中部區域(0.8 m)內單元為加厚殼單元，兩側區域(0.2 m)殼單元厚度不變。

圖11為未加固、間隔環加固和全部環加固的襯砌管片頂部中心節點的荷載系數-豎向位移變化曲線比較?？芍醇庸獭㈤g隔環加固和全部環加固的極限荷載系數分別為3.522，3.813和4.149，對應豎向位移分別為55.27，60.73 mm和72.73 mm。間隔環加固、全部環加固后管片的極限承載力相對未加固時分別提高了約8.26%，17.80%；HPF加固可有效提高管片的極限承載力，且后者加固效果更為顯著。

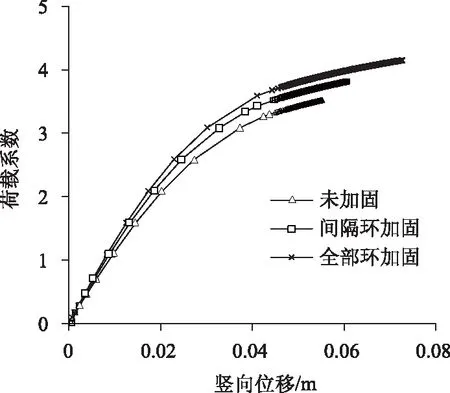
圖11 荷載系數-豎向位移變化曲線比較Fig.11 Comparison of curves of load coefficient vs. vertical displacement

值得指出的是，由于本節主要考慮HPF加固對盾構管片結構整體極限承載力的影響，并未涉及細部構造問題，因而采用局部加厚的簡化處理方式是具有一定參考價值的，且計算便捷快速。至于更為精細的砂漿鋼筋網加固模擬及其與管片-界面黏結效果的影響，有待后續進一步的研究。

5 結論

本研究采用15環殼-彈簧精細結構模型，對其應力應變和極限承載性能進行了研究，獲得以下主要結論：

(1)外部圍壓作用下，襯砌管片主要呈現為類似于扁橢圓的橫向整體變形形式，其中上、下側為向內凹進，左、右側為向外突出。這主要是由于土壓力一般要比側向土壓力大所導致的。

(2)正常使用工況的外部圍壓加載下，襯砌管片的最大Mises應力、最大全位移均出現在左右側和上下側的中心附近區域；最大Mises應力為13.5 MPa，約為單軸抗壓強度的0.585倍，具有較好的承載性能和安全余量；最大全位移為6.248 mm，對應整體變形橢圓度為4.03‰，符合規范小于6‰限值要求。

(3)極端工況的外部圍壓加載下，荷載系數隨著豎向位移增大的變化趨勢為線性迅速增大、非線性平緩增大和趨于平緩收斂的變化過程。管片結構的極限穩定荷載系數為3.522，具有較好的非線性穩定承載性能。

(4)HPF加固可有效提高管片的非線性極限承載力，間隔環加固、全部環加固后管片的非線性極限承載力相對未加固時分別提高了約8.26%，17.80%，具有較好的加固效果，且后者更為顯著。