孔底抵抗線對VCR爆破的影響研究
王文洋,羅志華,張宗國
(1.深圳市中金嶺南有色金屬股份有限公司 凡口鉛鋅礦, 廣東 韶關市 512000;2.中南大學 資源與安全工程學院, 湖南 長沙 410083)
0 引言
在開采過程中,由于孔底抵抗線過大或過小,使得爆炸能量過多的浪費,容易出現塊度分布不均勻的爆破效果與造成堵孔沖孔等爆破危害(見圖1(c))。為了最大化合理利用爆炸能量以提高爆破效果,改善礦山經濟效益,研究孔底抵抗線以控制爆炸效果對現場生產有很大的實踐意義。許多學者對爆破抵抗線進行了分析研究,如:姜永恒等[2]針對某金礦大塊率高的問題,運用數值模擬軟件對采場扇形孔進行模擬,分析了巖體內部質點的有效應力峰值,確定了中深孔爆破最優抵抗線和孔底距;何闖等[3]研究抵抗線與自由面對爆破振動的影響,得出爆破振動受自由面與最小抵抗線的共同影響;沈慧明等[4]采用理論分析的方式,得出適當調整抵抗線可以改善爆破效果;何士靄[5]通過合理的裝藥設計,使得爆破塊度、爆堆位移在合理范圍之內;李育等[6]采用減小前排裝藥抵抗線來控制爆破振動;魏兆云等[7]通過理論計算的方式確定爆破中抵抗線參數來控制爆破效果。綜上可知,多數研究均采用數值模擬的手段研究抵抗線,為了研究大直徑深孔爆破中孔底抵抗線對爆破效果的影響,本文采用數值模擬方法,對不同孔底抵抗線下的等效漏斗半徑與等效漏斗體積進行對比分析,優選合理的孔底抵抗線以改善現場爆破效果。
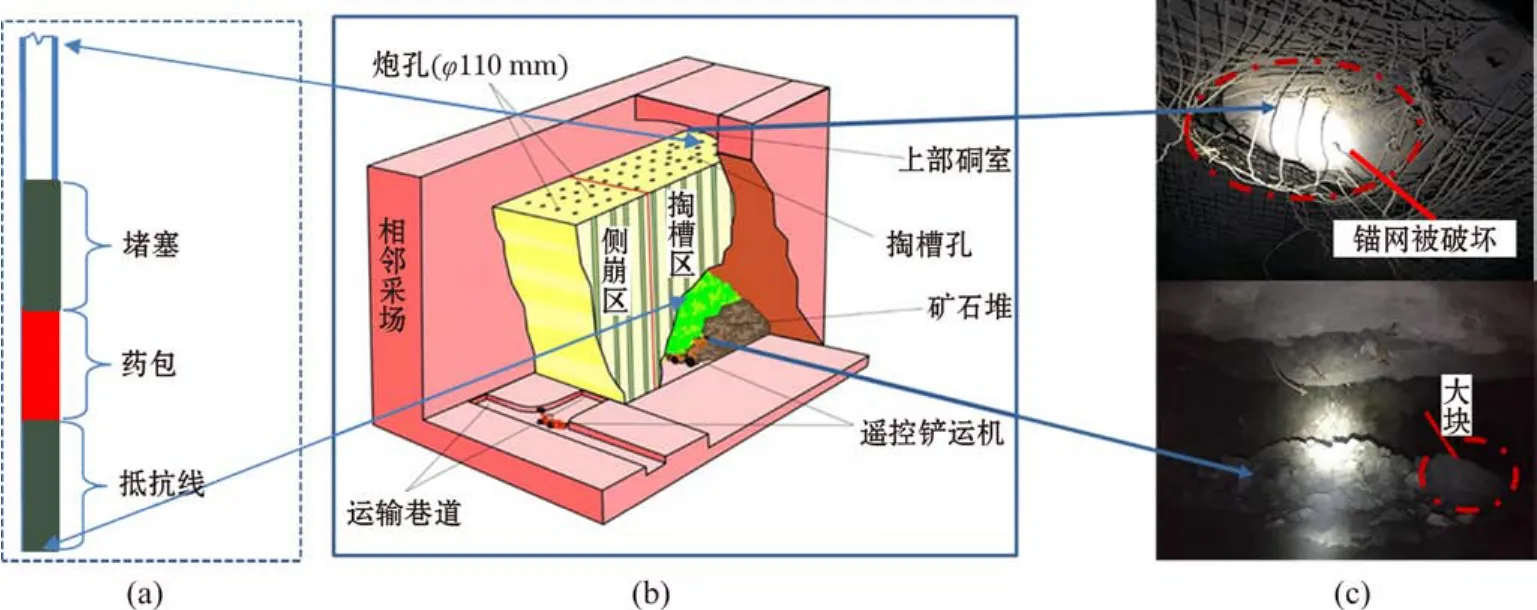
圖1 采礦工藝
1 數值模擬
1.1 模型建立
為了研究孔底抵抗線對爆破效果的影響,采用數值模擬方法分析爆炸過程中試塊內部應力變化情況,數值模擬中的炸藥、模型材料等與現場實際基本一致,模擬抵抗線為變量。本文的主要研究對象為抵抗線,為了方便劃分網格,數值模擬中將原藥包長度為0.6 m通過幾何相似比例縮放為3 cm,相似系數為20,模擬共分為5組,孔底抵抗線分別為3 cm、4 cm、5 cm、6 cm、7 cm。
如圖2所示,模型長、寬、高分別為40 cm、40 cm、30 cm,炸藥直徑為8 mm,長度為3 cm;其中孔底抵抗線大小為變量,其中藥包上下層均為堵塞物,模型中ALE空間的直徑為5倍炮孔直徑,ALE與部分石塊單元重合。模型中忽略重力的影響。巖石模型單元大小為5 mm×5 mm,炸藥、堵塞、ALE采用漸變網格。

圖2 四分之一模型示意
1.2 材料參數選取
1.2.1 炸藥的材料模型與其狀態方程
在LS-DYNA程序之中,炸藥材料模型采用8號材料模型,炸藥的狀態方程為“*EOS_JWL”,此方程忽略炸藥的化學反應方式而只考慮爆轟,經過大量試驗數據修正,JWL狀態方程如下[8-10]:
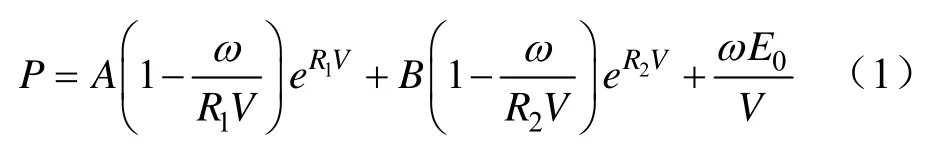
式中,P為爆轟壓力,Pa;E0為單元最大面積,m2;V為爆轟產物相對體積,m3;ω為格林愛森參數;A、B、R1、R2均為表征炸藥物理特性的常數。
1.2.2 混凝土RHT材料模型
本文數值模擬采用混凝土 RHT本構模型[12],該模型中的彈性極限面方程、最大失效面方程和殘余強度方程可用于描述混凝土在爆炸沖擊荷載作用下的初始屈服強度、失效強度和殘余強度的變化規律。
1.2.3 炮泥材料模型
卷積神經網絡可以用來處理并且分析多種多樣的圖像,卷積神經網絡本身建立于深度學習技術的前提下。具體在交通運用中,針對卷積神經網絡有必要明晰其中的多層次網絡架構,從而將其轉變成矩陣表示的完整神經網絡。在此基礎上,對于相應的原始圖像予以輸入處理,然后矩陣系統即可憑借當前輸入的各項信息來判定整個矩陣形態,從而選擇不同顏色來表示各個相應的圖片信息。針對輸出類別而言,對此設置了1000的默認值。在現實運用中,如果能靈活運用上述圖像處理,則可以運用圖片預測的方式來實現針對雨雪天氣的精確預測。
本文中炮孔采用炮泥進行堵塞,選用土壤和泡沫材料模型(*MAT_SOLI_AND_FOAM)。相關參數見表1至表4。

表1 炸藥參數

表2 炸藥狀態方程參數
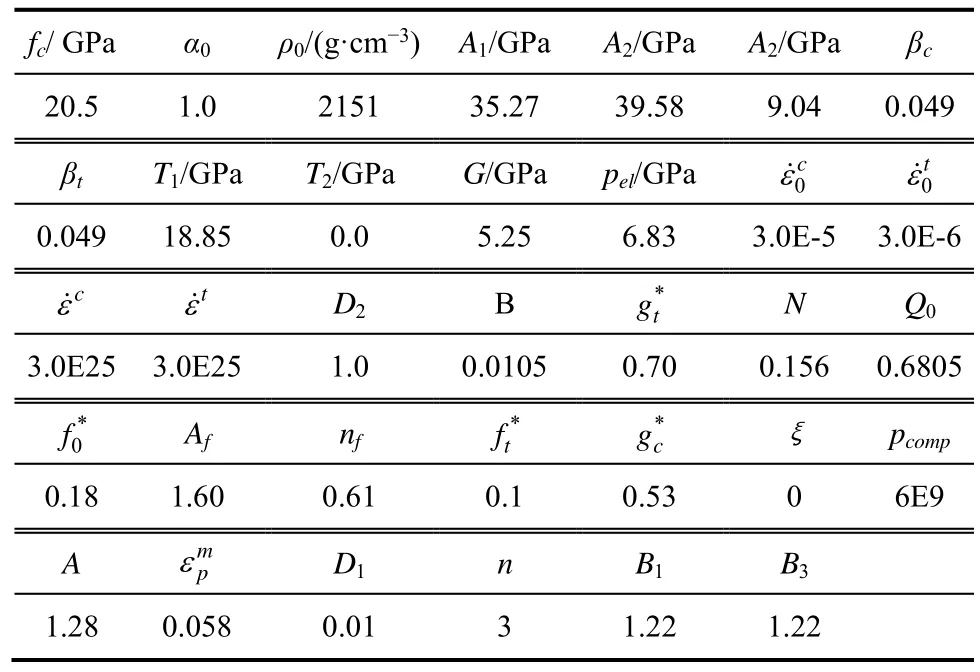
表3 試塊RHT材料模型的計算參數
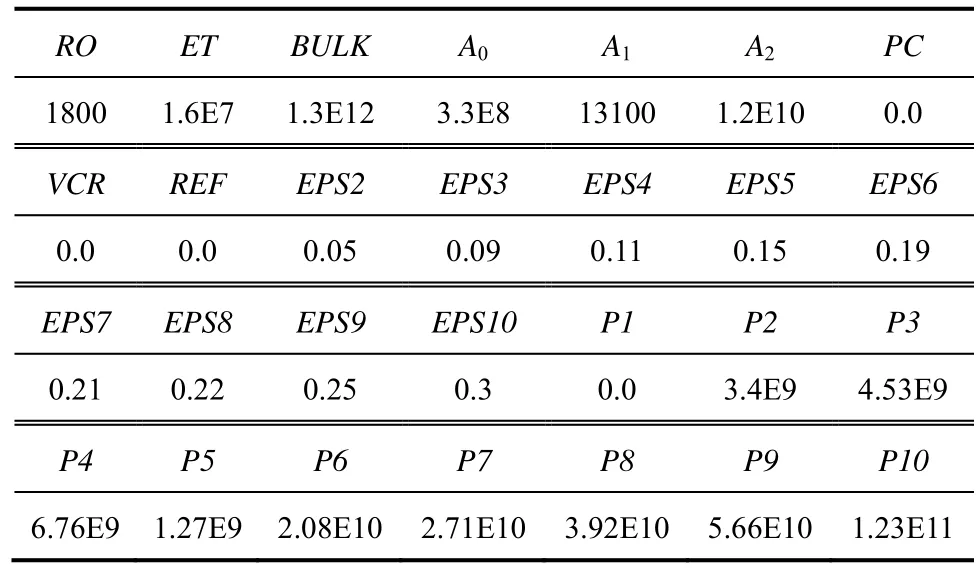
表4 炮泥材料模型的計算參數
1.3 爆破過程
在后處理軟件(LS-PREPOST)中進行分析,當損傷值達到0.7時,巖石發生破壞,因此,模擬模型損傷值下線為 0.7,為了模擬爆炸整個過程,以孔底抵抗線為4 cm試驗為例,模型內部損傷云圖演化過程如圖3所示。同時,為方便觀看漏斗形狀,將模型沿XZ面旋轉90°。
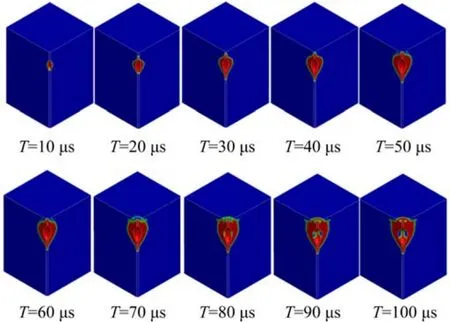
圖3 模型失效演化云圖
由圖3可知,在數值模擬過程中,藥包在10 μs時完全響應,爆炸應力波繼續往模型四周傳遞,藥包周圍發生破壞;10~40 μs時,損傷范圍逐漸沿著炮孔向自由面發展,模型內部形成破碎圈;40~60 μs時,損傷范圍發展至模型下表面(自由面),爆破漏斗初步形成,漏斗半徑較小,有待進一步擴展;60~90 μs時,該時期為漏斗半徑擴展時期,應力波的反射拉伸導致爆生氣體膨脹快速排出孔外,致使爆破漏斗半徑進一步擴大并達到峰值。90~100 μs時,很明顯可以看出,該時期漏斗直徑基本沒有變化,模型表面的損傷區域增大是由于模擬過程中應力波在模型中無法完全消耗,導致應力波在模型面不斷發生反射,導致損傷區域較大。綜上,將100 μs看作試驗中爆炸過程的終止時間點。
1.4 不同抵抗線下爆破效果分析
通過對堵塞長度為2 cm,孔底抵抗線大小為3 cm、4 cm、5 cm、6 cm和7 cm時進行數值模擬計算,并對其形成的爆破漏斗進行分析。圖4中依次為3~7 cm堵塞長度下等效爆破漏斗模型。
由圖4可知,在孔底抵抗線為7 cm時,爆炸沒有形成爆破漏斗,模型表面基本沒有破壞,而孔底抵抗線為4 cm時,爆炸形成的爆破漏斗半徑最大,爆破漏斗的半徑隨孔底抵抗線的增大先增大后減小。以上結果說明,抵抗線能改變藥包爆炸能量的作用范圍,適當的抵抗線能有效減小能量在炮孔中的流失,最大化利用爆炸能量,進而改善爆破效果。為定量描述爆破效果與孔底抵抗線之間的關系,將各方案形成的等效爆破漏斗半徑與等效漏斗體積進行統計(D0>0.7的單元),如圖4所示。
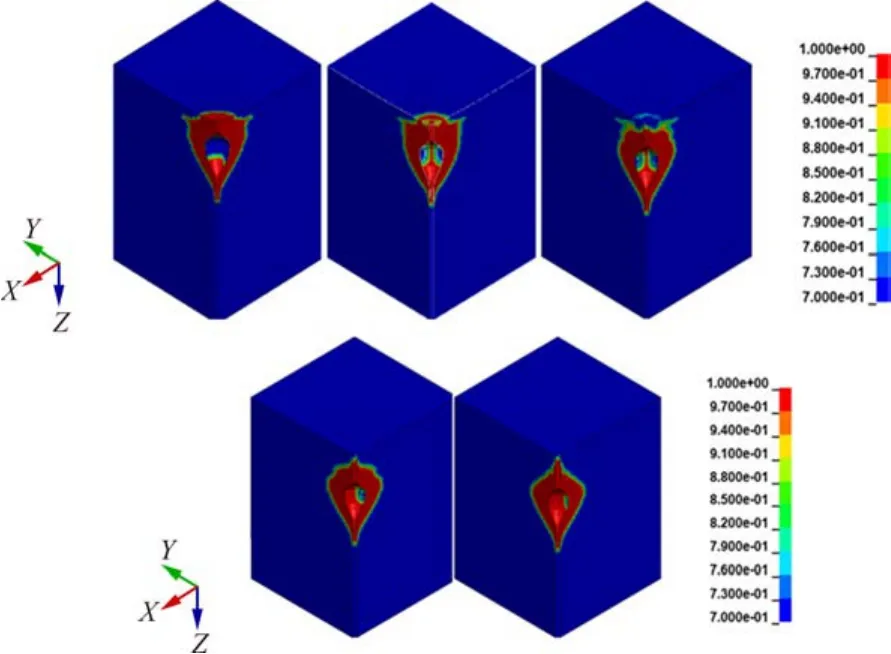
圖4 不同孔底抵抗線下爆破漏斗損傷模型
由圖5可知,孔底抵抗線較小時,大量的爆生氣體快速的從下部孔口沖出,導致炸藥能量作用于巖石的比例減小,造成了炸藥能量的損失浪費。隨著抵抗線的增大,爆破漏斗的半徑與體積相應的增大,但當抵抗線大于4 cm時,爆破漏斗的半徑出現拐點,當抵抗線大于5 cm時,爆破漏斗的體積也開始出現下滑。說明抵抗線的增大提高了藥包的作用深度,合理的抵抗線能夠有效改善爆破效果。

圖5 不同抵抗線下爆破漏斗半徑與損傷體積
1.5 不同測點應變對比
在數值模擬中,各測點按照模型試驗中的應變監測點布置,提取各監測點的應變進行分析,如圖6、圖7所示。
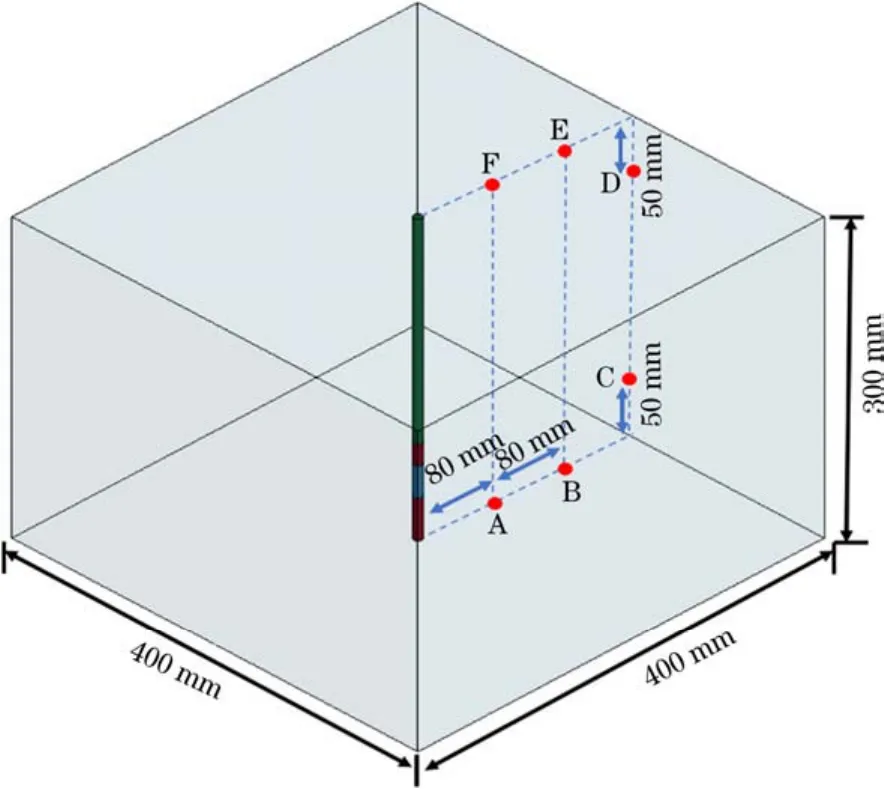
圖6 測點布置
由圖7可知,各監測點在2.5 ms時,有效塑性應變值趨向穩定,監測點 A、B、C的有效塑性應變值與初始應變率也較高,遠遠高于其他監測點。監測點D、E、F的應變值變化較小,且時間短暫,其有效應變數值大小排序為:A>B>C>F>E>D,爆破出現漏斗,炸藥主體能量沿炮孔向下表面傳遞,模型下表面的應變值遠遠高于其他表面質點的應變值。研究表明,應變值與初始應變率隨著炸藥的距離增大而減小。
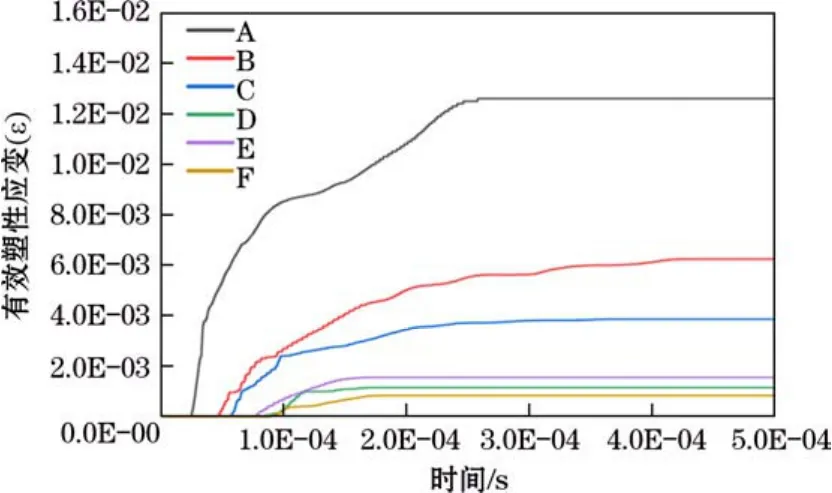
圖7 測點有效塑性應變
2 工程實例
由模擬結果可知,孔底抵抗線抵抗線為 5 cm時,其爆破效果較好,為了更好地驗證模擬成果,通過相似試驗,相似系數為20,現場試驗對應的孔底抵抗線為1 m,其裝藥結構如圖1(a)所示,采場爆破效果如圖8所示。圖8(a)中,采場上部硐室頂板錨網沒有出現明顯的破壞,圖8(b)中,下部硐室爆堆整體塊度較為均勻,達到生產過程中塊度破碎要求。試驗表明,該孔底抵抗線條件下能較好地改善現場爆破效果。

圖8 現場試驗爆破效果示意
3 結論
(1)通過數值模擬相似模擬試驗可知,隨著孔底抵抗線由3 cm增大至7 cm,模擬結果表明,其等效漏斗半徑與體積均呈先增大后減小,其中孔底抵抗線為 5 cm,等效漏斗體積最大,爆破效果最好。
(2)通過分析自由面上各監測點有效塑性應變可知,應變值與初始應變率隨著炸藥距離的增大而減小。
(3)將研究成果應用于礦山采場爆破,現場爆破效果能較好地滿足生產需求,降低沖孔,改善爆破塊度,表明通過調整 ⅤCR爆破孔底抵抗線來優化爆破效果具有一定現場指導意義。

