石墨烯莫爾超晶格的晶格弛豫與襯底效應*

詹真 張亞磊 袁聲軍2)?

1) (武漢大學物理科學與技術學院,武漢 430072)

2) (武漢量子技術研究院,武漢 430206)

當兩個晶格常數不同或具有相對轉角的二維材料疊加在一起時,可形成莫爾超晶格結構,其電學性質對層間堆垛方式、旋轉角度和襯底具有很強的依賴性.例如,雙層石墨烯的旋轉角度減小到一系列特定的值(魔角)時,體系的費米面附近出現平帶,電子-電子相互作用顯著增強,出現莫特絕緣體和非常規(guī)超導量子物態(tài).對于具有長周期性的莫爾超晶格體系,層間相互作用所引起的晶格弛豫會使原子偏離其平衡位置而發(fā)生重構.本文主要圍繞晶格自發(fā)弛豫和襯底對石墨烯莫爾超晶格物性的影響展開綜述.從理論和實驗的角度出發(fā),闡述旋轉雙層石墨烯、旋轉三層石墨烯、以及石墨烯與六方氮化硼堆垛異質結等體系中自發(fā)弛豫對其能帶結構和物理性質的影響.最后,對二維莫爾超晶格體系的研究現狀進行總結和展望.

1 引言

過去十多年,低維量子體系由于獨特的結構和極強的可調性等特點,成為凝聚態(tài)物理和材料科學研究的熱點[1,2].石墨烯是第一個由實驗制備的穩(wěn)定層狀二維材料[3].將兩層石墨烯以不同角度堆疊可形成莫爾超晶格結構,其性質對層數、層間的堆垛方式和襯底有極強依賴性[4,5].兩層石墨烯堆疊并旋轉一定角度,當轉角減小到1.1°附近(此角度稱為魔角),體系的費米面附近出現平坦能帶[4].在平帶中,電子的運動速度趨于零,具有極小的動能,滿足出現強關聯的基本條件.2018 年,實驗研究人員在魔角石墨烯中觀察到強電子-電子相互作用導致的莫特絕緣體和非常規(guī)超導態(tài)這兩種關聯量子物態(tài)[6,7].隨后,通過門電壓、轉角、應變、垂直電場和外磁場等調控方式,在石墨烯莫爾超晶格中實現了拓撲絕緣體[8,9]、超導[10]、鐵電[11]、鐵磁[12]以及量子反常霍爾 (quantum anomalous Hall,QAH)效應[13]等物理現象.這些新奇現象迅速吸引了大批研究者的目光,并發(fā)展出了一門新的科學分支,即轉角電子學 (twistronics)[14].

最近實驗和理論研究表明[15-18],當旋轉雙層石墨烯(twisted bilayer graphene,TBG)的轉角小于1.2°時,體系的晶格結構和電學性質發(fā)生明顯的重構,出現巨大的贗磁場[19].隨著轉角逐漸減小,晶格重構效應會進一步增強,在極小角度的TBG中出現三角網格結構和一維拓撲態(tài)[20].通常情況下,將石墨烯放置在六方氮化硼(hexagonal boron nitride,hBN) 襯底上,當二者晶向一致時,會形成石墨烯/hBN 莫爾超晶格.研究發(fā)現hBN 襯底會抑制魔角石墨烯中超導態(tài)的產生[12,13,21].前期研究表明,魔角石墨烯中超導態(tài)和絕緣態(tài)存在共生關系,但在魔角石墨烯上疊加一層WSe2時,超導相和絕緣相由共生關系變成競爭關系,且超導態(tài)能夠在更小的轉角下存在[22].綜上所述,晶格弛豫和襯底會顯著改變石墨烯莫爾超晶格的晶格結構和電子性質,出現很多新的物理現象.

本文將圍繞晶格弛豫和襯底對石墨烯莫爾超晶格性質調控的近期研究展開綜述,內容包括晶格弛豫對魔角TBG 和魔角旋轉三層石墨烯(twisted trilayer graphene,tTLG)的晶格結構和電學性質影響,石墨烯和氮化硼莫爾超晶格中的能隙、超晶格狄拉克點的出現和反演對稱性打破等現象.

2 理論模型與方法

2.1 石墨烯莫爾超晶格的晶格結構

當單層石墨烯與另外一層石墨烯或其他層狀二維材料以范德瓦耳斯力堆垛時,在特定條件下會形成長周期的莫爾條紋(moiré pattern).莫爾條紋的長度由兩層材料的晶格失配和彼此之間形成的旋轉角度θ決定.具有嚴格實空間周期性的超晶格結構只存在于某些特定角度,即所謂的“可公度”(commensurate)角度.假設兩層晶格結構的基矢分別為(at1,at2)和(ab1,ab2),其對應倒格子基矢分別為(kt1,kt2)和(kb1,kb2).這些基矢可以寫成Park-Madden 矩陣的形式[23]:

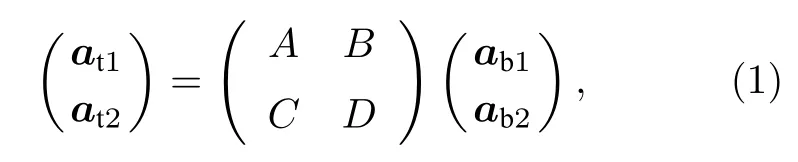
其中,為了滿足可公約條件,A,B,C,D均為有理數,由莫爾條紋長度決定.通常情況下,樣品的莫爾條紋可由掃描隧道顯微鏡(scanning tunneling microscope,STM)清晰地觀測到.為了精確求解(1)式中的矩陣元,需要將超晶格結構的STM 圖進行(快速)傅里葉變換,并定義莫爾超晶格的倒格子基矢為(km1,km2),則可公度性可用公度參數(i,j,k,l,m,n,q,r)描述為

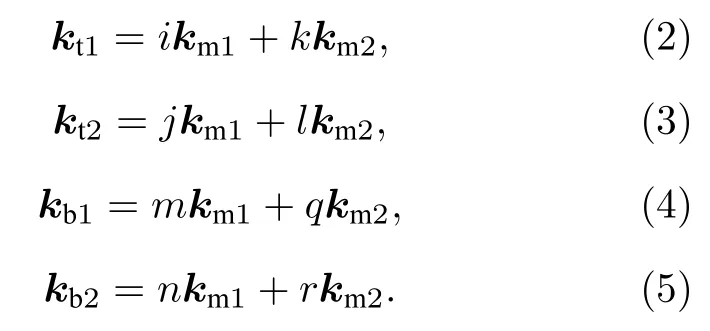
由(1)式—(5)式可得:

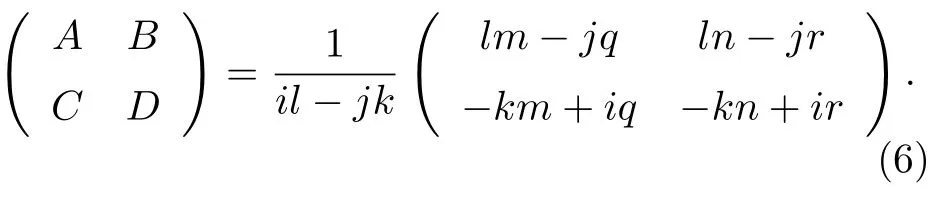
一旦莫爾條紋的周期(STM 圖中兩個亮點間的距離,如圖2(a)所示)確定,即可通過(2)式—(5)式求得一組公度參數,且其解具有唯一性,可進一步確定超晶格結構的應變ε和旋轉角度θ.對于由兩層六角蜂窩狀晶格組成的超晶格結構,假設兩層的晶格矢量之比分別為,并且第二層相對于第一層的旋轉角度分別為θ1=(at1,ab1)和θ2=(at2,ab2).則兩層的晶格矢量可由推廣的伍德記號(extended Wood’s notation)描述[24]:

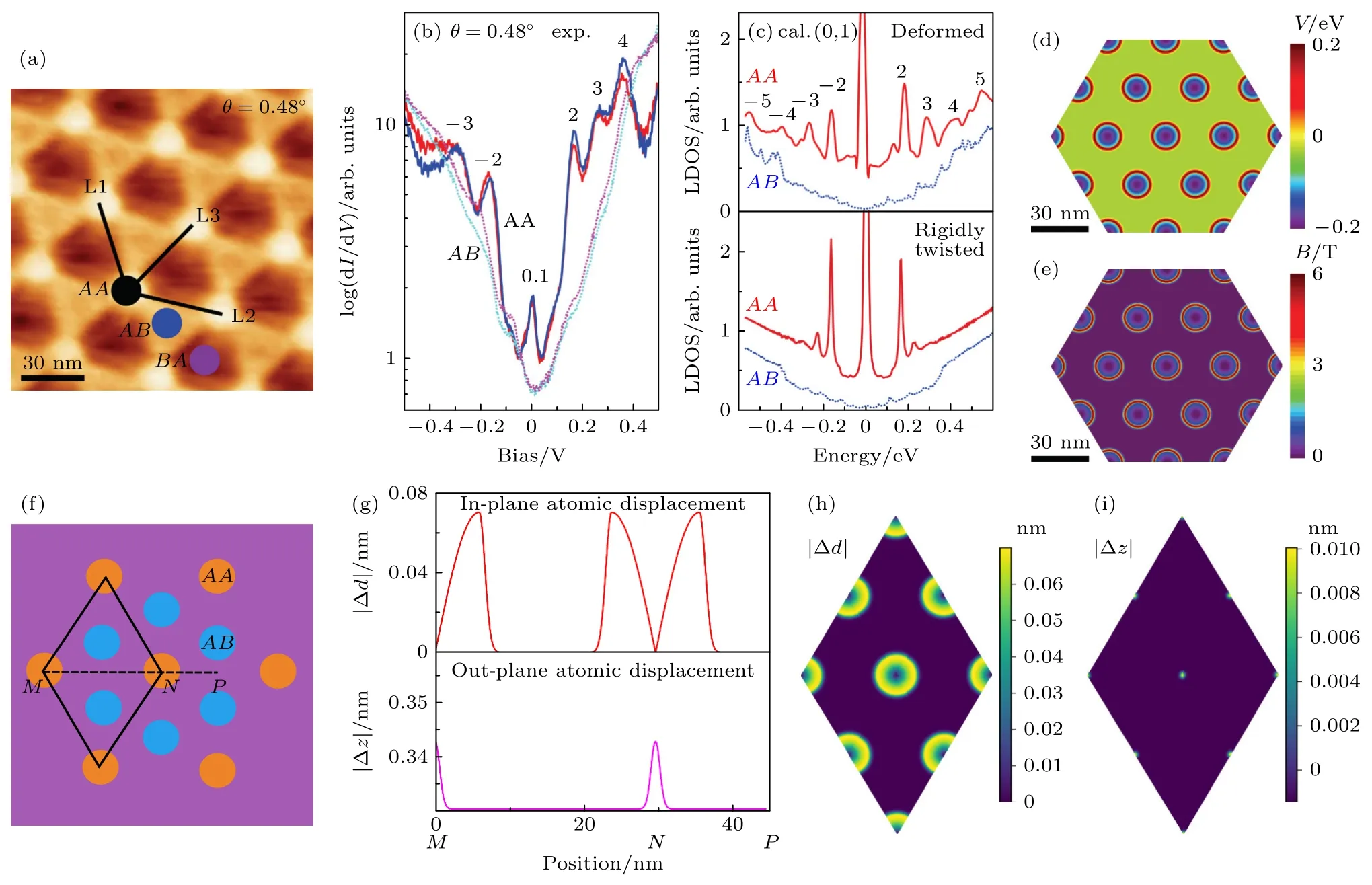
圖2 (a) θ=0.48° 的TBG 的STM 形貌圖 (100 nm ×100 nm,超晶格格矢 L1≈L2≈L3≈29.6 nm,STM 圖在V=100 mV 和It=1.0 nA 下采集);(b) 超晶格結構中AA 和AB 區(qū)域的STS,兩條實(虛)線表示探測不同AA (AB)位置的STS,證明實驗數據的可重復性;(c) TBG 非弛豫結構(上)和弛豫結構(下)中AA 和AB 區(qū)域的LDOS;(d) 形變勢能V 的分布;(e) 贗磁場B 的分布;(f) θ=0.48° 的TBG 理論計算模型圖;(g) 路徑M-N-P 上原子在平面內(|Δd|)和z 方向上(|Δz|)的位移;(h),(i) 原子分別在平面內(h)和z 方向上(i)位移的實空間分布圖[19]Fig.2.(a) STM topography image (100 nm × 100 nm) for TBG with θ=0.48° (The three moiré wavelengths are L1≈L2≈L3≈29.6 nm,sample bias V=100 mV,tunneling current It=1.0 nA);(b) logarithmic dI/dV spectra measured at AA and AB regions (The two solid/dashed lines were taken at different AA/AB regions to show reproducibility,and curves are vertically shifted for clarity);(c) calculated LDOS in the AA and AB regions for deformed (upper) and rigidly twisted (bottom) cases;(d) calculated local potential V;(e) calculated pseudo-magnetic fields B;(f) schematic model of the moiré pattern of TBG with θ=0.48°;(g) absolute magnitude of different in-plane atomic displacements and out-of-plane displacements for the deformed system along the path M-N-P;(h),(i) maps of the absolute magnitude of the in-plane atomic displacement |Δd| (h) and out-of-plane displacement |Δz| (i) in deformed systems[19].

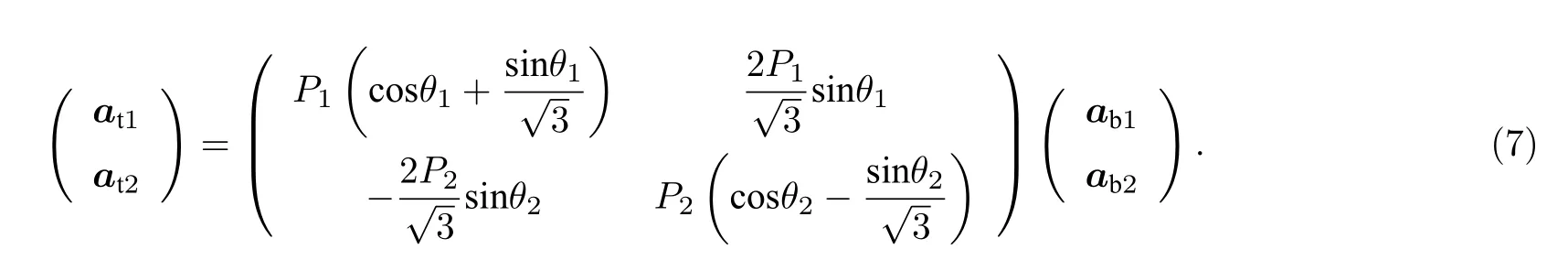
由(1)式和(7)式可求得參數P1,P2,θ1和θ2為

單軸異質應變(uniaxial heterostrain)和雙軸異質應變(biaxial heterostrain)分別為

超晶格的原胞可能包含一個或多個莫爾晶胞.若無特殊說明,本文討論的超晶胞原胞只包含一個莫爾晶胞.以旋轉角度為θ=6.01°的TBG 為例,圖1 為其結構示意圖,超晶胞的基矢am1和am2對應一組公度參數(i,j,k,l,m,n,q,r)=(11,5,—5,6,11,6,—6,5),推廣的伍德記號為(P1Rθ1×P2Rθ2)=(1R6.01×1R6.01)(R是伍德記號標準形式中的R,代表兩層材料中對應基矢的旋轉角度差,即文中θ1和θ2),一個原胞包含364 個原子.莫爾超晶格體系包含4 種高對稱結構,分別是AA堆垛、AB堆垛、BA堆垛和疇壁(domain wall,DW)堆垛.若TBG 體系中不存在應變,則莫爾條紋長度和轉角滿足簡單關系式am1/m2=a/[2sin(θ/2)],其中a是石墨烯的晶格常數.

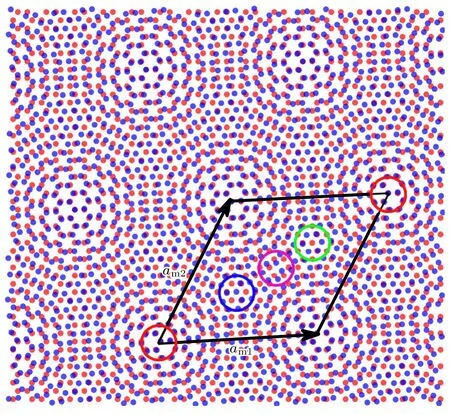
圖1 θ=6.01° 時TBG 結構示意圖(黑色實線框表示莫爾超晶格的原胞;圓圈表示4 種高對稱堆垛結構,分別為AA 堆垛(紅色)、AB 堆垛(藍色)、DW 堆垛(紫色)和BA堆垛(綠色))Fig.1.Schematics of the atomic configuration of TBG with θ=6.01°(The moiré supercell is outlined in black line.High-symmetry stacking regions of AA,AB,DW and BA are marked by the red,blue,purple and green circles,respectively).

2.2 低能有效模型

石墨烯莫爾超晶格的低能電子結構可由低能有效連續(xù)模型(low-energy effective continuum model)加以描述[4,25,26].首先考慮多層轉角石墨烯的層間躍遷項:

(16)式表明,當q長度大于倒格子基矢長度|kt1|時,動量空間躍遷振幅會快速衰減,故(15)式中有效的躍遷項只發(fā)生在第一層石墨烯中動量為k的態(tài)與第二層動量為k,k+km1和k+km1+km2的態(tài)之間,以及第二層石墨烯中動量為k的態(tài)與第一層動量為k,k-km1和k-km1-km2的態(tài)之間.

在長波近似下,雙層轉角石墨烯的低能能譜可用六個動量值的哈密頓量來描述,即第一層中的k,k-km1和k-km1-km2和第二層的k,k+km1和k+km1+km2.此時體系低能部分有效哈密頓量可約化為以(A,B,A′,B′) 為基矢的4×4 矩陣[26,27]:

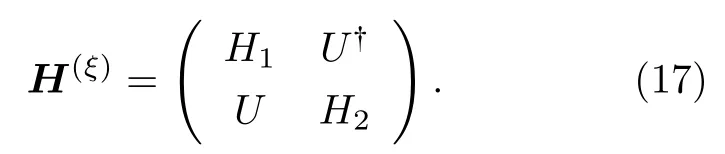
這里,Hl=1,2是l層內哈密頓量,由外爾方程給出:

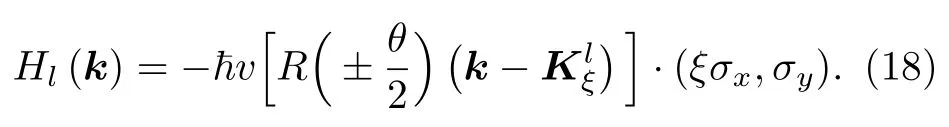
U是有效層間耦合,由三項層間耦合組成:

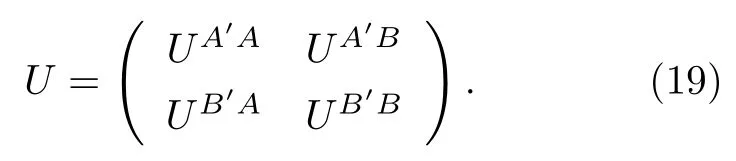
根據(17)式中的哈密頓量,可以得到TBG 的低能能帶色散關系.

在有效連續(xù)模型中,晶格弛豫和應變對電子結構的影響可通過對(17)式中矩陣元的調整加以研究.如文獻[27]中討論了石墨烯莫爾超晶格層間結構弛豫的影響,由于石墨烯莫爾超晶格AA堆垛區(qū)域的層間結合能較AB和BA堆垛區(qū)域更高[28-30],莫爾超晶格自發(fā)弛豫后AA堆垛區(qū)域的層間距更大,從而使(19)式中子晶格間的躍遷振幅不再相等來調整能帶結構.

2.3 緊束縛模型與大尺度計算方法

緊束縛模型(tight-binding model)是凝聚態(tài)物理中廣泛應用的理論模型,對于周期性比較小的體系可以得到直觀的電子結構,同時也可以處理周期性很大或沒有周期性的超大體系.單電子近似下,緊束縛模型的哈密頓量可以表示為

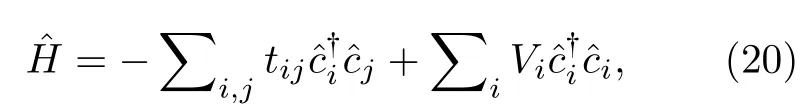
其中tij表示i,j軌道間的躍遷振幅;Vi表示第i個軌道的占位能;為第i個軌道上的產生、湮滅算符.對于石墨烯體系,為了研究結構弛豫對電子結構的影響,可使用Slater-Koster 近似計算軌道間的躍遷振幅[31]:

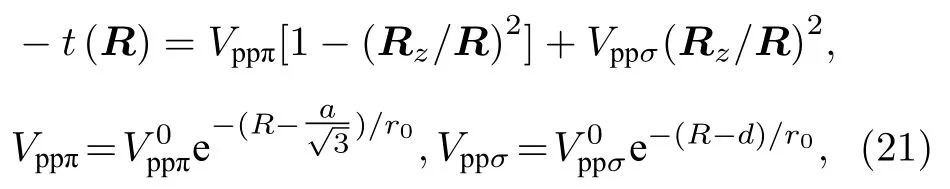
其中,R為軌道間距離,Rz為z方向的分量;r0是躍遷衰減長度;是單層材料中最近鄰軌道間躍遷能;是層間垂直方向上兩個軌道的躍遷能[32].

由于莫爾超晶格的晶胞包含原子數目過多,使用對角化方法求其本征態(tài)在數值上會遇到較大的困難.針對復雜的大尺度體系,可采用基于含時薛定諤方程的緊束縛傳播方法(tight-binding propagation method,TBPM)繞開對本征態(tài)的計算[19,33-35].TBPM 是建立在對含時薛定諤方程的精確數值求解之上,不對體系進行任何對角化處理,可以對體系的各種物理性質進行快速而準確地計算,且計算消耗和體系大小呈線性關系.如運用Chebyshev多項式展開的方法,可以從一個初始波函數直接準確地計算出其他任意時刻的波函數.首先介紹在TBPM 中對時間演化的處理方法.根據含時薛定諤方程,對于隨機選取的初始態(tài)波函數|ψ0〉=,其時間演化態(tài)為

在數值計算中,使用有限大小的固定時間步長 Δt,通過Chebyshev 多項式對時間演化算符進行展開可得到[33]

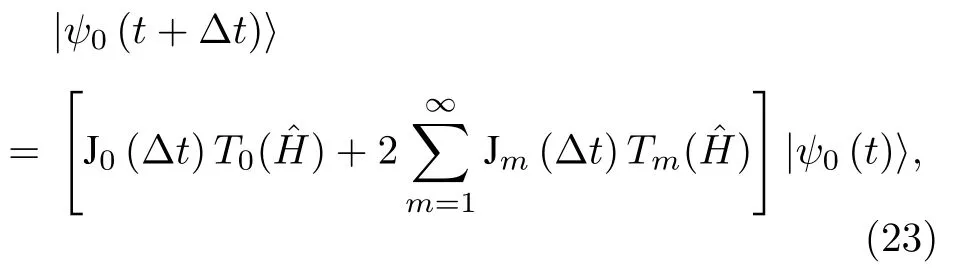
其中,Jm為m階第一類貝塞爾函數;Tm為m階切比雪夫多項式,可通過遞推關系迭代求得,即

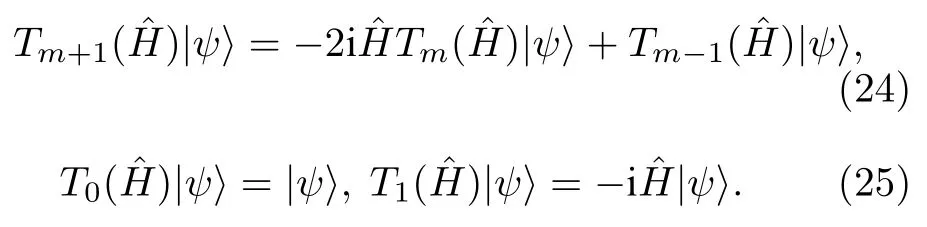
通過(23)式,可求得一系列基于同一個初始態(tài)的時間演化波函數.體系的電學、光學、輸運和等離激元性質可以進一步通過波函數的含時演化得到.下面以電子態(tài)密度(density of state,DOS)為例介紹如何通過時間演化方法計算體系物理性質:

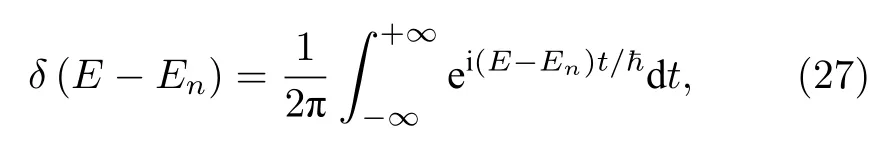
通過對含時演化態(tài)與初始態(tài)的內積進行傅里葉變換,并對基于不同的隨機初始波函數的結果進行統(tǒng)計平均[36],便可得到DOS:

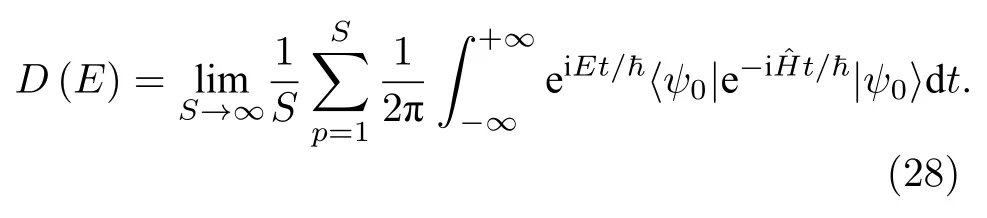
類似地,通過對不同時間的波函數本身進行傅里葉變換,可以得到特定能量的準本征態(tài)(quasieigenstates):

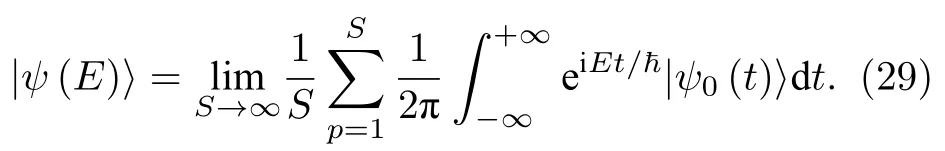
目前,TBPM 方法已集成在開源軟件TBPLaS(Tight-Binding Package for Large-scale Simulation)[37]中.這是一款通用的大型緊束縛模型計算軟件,不僅可以完成能帶計算,還可以應用到超大體系的各種電學、光學、輸運和等離激元性質計算,模擬體系的尺寸跨度達到近10 個數量級,可以模擬數十億個原子(格點)的復雜量子體系,非常適合莫爾超晶格體系的電學、光學、輸運和等離激元性質的計算.

3 石墨烯莫爾超晶格中的自發(fā)弛豫

旋轉角度作為新的自由度,可以有效調控旋轉石墨烯體系的電學性質,給石墨烯體系帶來許多新奇的物理現象.本節(jié)主要研究旋轉石墨烯體系的弛豫現象以及弛豫對不同轉角體系的晶格結構和電學性質的影響.

3.1 TBG 莫爾超晶格

在TBG 能帶圖中,K和K′點的中間位置有一個鞍點M,對應DOS 分布的極大值,稱為范霍夫奇點(van Hove singularity,VHS)[5,38,39].實驗和理論研究發(fā)現,TBG 的VHS 出現在低能部分,且其能量位置隨旋轉角度減小逐漸接近費米能級[5,38,39].例如,當旋轉角度減小到 1.16°時,VHS 離費米能級的距離只有6 meV.當旋轉角度接近 1.05°,體系在費米面附近出現平坦的能帶,對應的角度稱為第一魔角[4,39].魔角的定義主要有兩種: 一是超結構倒空間中K和K′點的費米速度降為0;二是體系在費米面附近的能帶帶寬最小,并且最低能量電子態(tài)距離高能量電子態(tài)的帶隙值最大[40].理論研究發(fā)現,TBG 有一系列魔轉角,且魔轉角之間滿足,其中=1.05°是第一魔角[4,39].由于理論模型和計算參數的差異,第一魔轉角的數值并不是定值,而是出現在1.0°—1.5°之間.2018 年,麻省理工學院Jarillo-Herrero 課題組[6,7]成功制備出魔角石墨烯,并在體系中觀察到強電子-電子相互作用導致的莫特絕緣體和非常規(guī)超導態(tài)這兩種關聯量子物態(tài).隨后,在這個強關聯體系中又發(fā)現了鐵電、鐵磁、拓撲、QAH 效應等一系列強關聯現象[8,11].

兩層石墨烯以AA堆垛并旋轉一定角度后,體系中存在AA,AB,BA和DW四種高對稱結構,如圖1 所示.其中AB和BA堆垛(又稱Bernal 堆垛)是能量最低的堆垛方式,DW堆垛能量次之,AA堆垛的結合能最高[15].一方面,不同堆垛的能量差異產生了面內應力,使原子偏離平衡位置,從而增加Bernal 堆垛區(qū)域的面積,減小層間相互作用能;另一方面,原子在面內移動產生的應力會阻止其進一步偏離原來位置.基于以上原因,莫爾超晶格中原子會偏離其原有位置,發(fā)生結構形變,因此,晶格重構是層間能量達到最小值和位移產生應力的競爭結果[15,41].理論研究發(fā)現,當TBG 的轉角小于1.2°時,體系發(fā)生明顯的晶格弛豫[15],影響小角度TBG 的晶格結構和電學性質[17,18,42].對于魔角石墨烯體系,晶格弛豫使平帶的帶寬由6 meV變?yōu)? meV,并且在Γ點打開帶隙,能隙值約為42 meV[43].Yoo 等[18]利用透射電子顯微鏡研究了小角度TBG 的結構,發(fā)現晶格弛豫使樣品重構成一系列三角形的AB和BA堆垛區(qū)域,同時,在AB和BA交界處產生疇壁,不同區(qū)域的疇壁形成一個三角網格.疇壁上存在無能隙的一維拓撲電子態(tài)[44],可以增強疇壁區(qū)域的光電導[45].結合STM 探測手段、掃描隧道譜(scanning tunnel spectrum,STS)技術和理論分析,目前已經確認TBG 中晶格弛豫會引起自發(fā)的贗磁場[19].

如圖2(a)所示,TBG 的STM 形貌圖展現出完美的六角對稱性,莫爾條紋長度通過測量亮點間距得到,分別為L1≈L2≈L3≈29.6 nm.隨后求解(1)式—(6)式得到一組公度參數(I,j,k,l,m,n,q,r)=(139,69,—69,70,139,70,—70,69),并求得其旋轉角度θ=0.48°.在莫爾條紋區(qū)域不同的位置進行STS 譜探測,如圖2(b)所示,AB堆垛區(qū)域的STS 譜沒有明顯的特征峰,呈現出AB堆垛雙層石墨烯的性質.另一方面,AA堆垛區(qū)域的STS 譜展現出一系列等能量間距的特征峰,與之前報道的結果截然不同[38].早先的理論與實驗研究表明,在角度 1.4°≤θ≤9.6°的TBG 樣品中,其STS譜在費米能級附近出現兩個VHS 峰,而不會出現一系列等能峰.

為了進一步探究STS 中等能量特征峰背后的物理起源,Shi 等[19]對這一結構進行計算分析.STS譜反映樣品表面的局域電子態(tài)密度(local density of states,LDOS).圖2(c)為采用緊束縛模型計算得到的LDOS.對于非弛豫結構的TBG,AA堆垛區(qū)域的LDOS 不存在等能量特征峰.隨后,通過在體系中加入晶格弛豫修正,新得到的理論結果與實驗十分相符.弛豫結構中原子在平面內和平面外的位移滿足如下公式[19]:

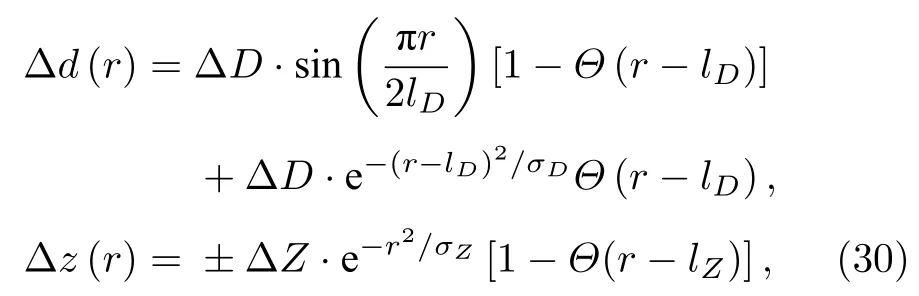
其中,r是x-y平面內弛豫原子距離最近鄰AA區(qū)域的長度;Θ是Heaviside 階躍函數; ΔD和 ΔZ分別是平面內和平面外最大位移量,其數值取決于旋轉角度θ[17];lD,σD,lZ和σD是常數.圖2(g)顯示的是原子沿路徑M-N-P的面內和面外位移,結果顯示AA堆垛區(qū)域的原子形變最大,與分子動力學弛豫結果一致[17].在旋轉石墨烯體系中,晶格弛豫在體系哈密頓矩陣中引入兩個勢參數,形變勢能V和贗矢勢A,其表達式為

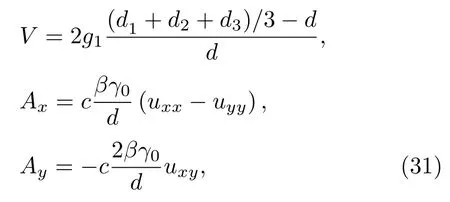
其中,石墨烯的形變勢能g1≈4 eV;d1,d2和d3是弛豫結構中最近鄰原子間距;石墨烯的碳-碳鍵長d=0.142 nm;常數因子c≈1,取決于具體模型中的化學鍵長;Grüneisen 參數β≈2;γ0是平面內最近鄰相互作用強度;uij是應變張量.形變勢能V以占位能的形式加入哈密頓矩陣,贗矢勢A通過改變原子軌道間的躍遷能來修正體系哈密頓量.對贗矢勢求旋度可得到贗磁場B=?×A,其絕對值近似為[41]

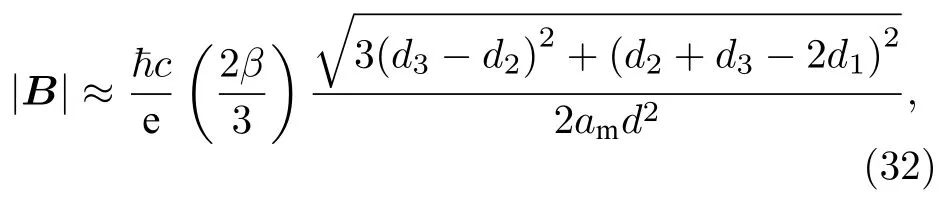
am是莫爾長度.圖2(d)和圖2(e)是采用(31)式和(32)式計算的形變勢能和贗磁場值.對于轉角θ=0.48°的TBG,晶格弛豫在體系中產生不均勻的形變勢能和贗磁場.其中形變勢能分布在AA堆垛區(qū)域,最大值是0.2 eV.類似地,非均勻的贗磁場以AA堆垛中心為原點,形成渦旋狀磁場,贗磁場最大值是6 T.AA堆垛區(qū)域的電子在贗磁場作用下出現了類似于真實磁場作用下的朗道量子化能級.但是,晶格弛豫產生的贗磁場沒有打破時間反演對稱性.值得注意的是,體系中的贗磁場是由于晶格自發(fā)弛豫產生的,并且隨著轉角減小,贗磁場值越大.下面進一步討論晶格弛豫對不同魔轉角體系的原子結構和電子性質的影響.

魔角石墨烯的特別之處是在費米面附近出現平坦的能帶[4],在平帶中電子的運動速度趨于零,具有極小的動能,滿足出現強關聯的基本條件.同時,平帶的電子態(tài)在實空間中高度局域在AA堆垛區(qū)域.目前,魔角雙層石墨烯的實驗和理論研究主要集中在第一魔角附近,更高階魔角的研究報道比較少.Huang 等[20]通過STM 觀察到旋轉角度為0.25° (第四魔角附近)的雙層石墨烯結構,并利用STS 探測到拓撲邊界態(tài).在小角度TBG 中,晶格弛豫使樣品重構成一系列AB和BA堆疊區(qū)域,并在AB-BA堆疊的交界處產生疇壁.在外加偏置電壓下,雙層石墨烯可在狄拉克點打開能隙并獲得非零的能谷陳數.疇壁兩側AB和BA兩種堆疊結構在某一特定能谷的能谷陳數符號相反,導致疇壁上存在無能隙的一維拓撲電子態(tài),并形成一維導電通道[20,46].Xu 等[47]觀察到電子在一維拓撲導電通道中產生的阿哈羅諾夫-玻姆效應(Aharonov-Bohm effect).同時,疇壁可以傳輸谷極化電流[48].晶格重構會調節(jié)材料中的振動和電子結構,導致電-聲耦合行為發(fā)生變化[42].Lu 等[49]在第二魔角附近觀察到一系列孤立的平帶,并通過強磁場下的輸運性質得到進一步證實.理論研究發(fā)現,隨著角度減小,由于晶格重構,AA堆疊區(qū)域急劇減小,從而導致高階魔角體系中不存在孤立的平帶[50].結合分子動力學模擬和緊束縛模型,在這里系統(tǒng)地闡述晶格弛豫對不同魔角石墨烯的結構、平帶以及平帶波函數在實空間分布的調控規(guī)律.

首先,利用分子動力學模擬軟件LAMMPS[51]對不同魔角體系進行晶格弛豫,然后采用(21)式將原子位移對層內和層間電子躍遷積分的修正加入緊束縛模型中.通過調節(jié)(21)式的緊束縛參數,將第一魔角對應的旋轉角度值定為θ=1.05°.在進行LAMMPS 弛豫時,層內相互作用和層間相互作用分別采用LCBOP[52]和Kolmogorov-Crespi[53]勢參數.若無特殊說明,本文均采用相同的層內層間勢參數對石墨烯莫爾超晶格進行晶格弛豫.這里主要研究三類魔角體系: 第一魔角(θ=1.05°)、第二魔角(θ=0.53°) 和第三魔角(θ=0.35°),對應公度參數(I,j,k,l,m,n,q,r)分別是(63,31,—31,32,63,32,—32,31),(125,62,—62,63,125,63,—63,62)和(189,94,—94,95,189,95,—95,94),相應晶胞所包含的原子數是11908,46876 和107164.由于這些魔角體系晶胞包含的原子數眾多,無論是基于密度泛函理論的第一性原理計算還是基于對角化的緊束縛模型計算都難以直接進行.因此,采用TBPM 方法來計算魔角石墨烯的LDOS 和DOS在實空間的分布.

圖3 是不同魔角體系中原子在平面內和平面外的弛豫結果.由于AA堆垛的結合能最高,因此AA區(qū)域的原子發(fā)生明顯偏移.原子在平面內圍繞著AA旋轉,形成“渦旋”結構,并且上下層原子旋轉方向相反.同時,TBG 在AA區(qū)域形成“突起”結構,即原子朝面外移動.因此,AA堆垛的層間距最大,AB堆垛的層間距最小.這些“突起”結構即STM 形貌圖觀察到的亮點.隨著角度減小,例如在高階魔角體系中,AA區(qū)域面積逐漸減小,AB和BA區(qū)域面積逐漸增大,同時AB區(qū)域由圓形變?yōu)槿切?并且在AB與BA區(qū)域間看到明顯的疇壁.特別是在第三魔角,體系主要由一維拓撲疇壁連接不同的AA堆垛區(qū)域,不同堆疊區(qū)域的疇壁形成一個三角網格,三角網格內是交錯排列的AB或BA堆垛結構.從圖3 可以明顯觀察到,由于晶格弛豫強度不同,高階魔角與第一魔角在結構上有顯著的變化.

圖3 (a)—(c) θ=1.05° (a),θ=0.53° (b) 和 θ=0.35° (c) 的面內應變張量 u(r) (白色箭頭表示原子在平面內的位移矢量;彩色條表示原子在面內的旋轉角度 Δθ=?×u,正值表示順時針旋轉;莫爾結構的晶胞由黑色邊框標記;3 個高對稱區(qū)域分別是AA,AB 和DW);(d)—(f) θ=1.05°(d),θ=0.53° (e)和 θ=0.35° (f)的層間距(ILS)在實空間的分布Fig.3.(a)—(c) In-plane strain u(r) in twisted bilayer graphene with (a) θ=1.05° ,(b) θ=0.53° and (c) θ=0.35° (The in-plane displacements are visualized with white arrows;the color data denotes the local value of the in-plane twist of the atoms with respect to their original position (Δθ=?×u),and the positive values indicate counterclockwise rotation.The moiré supercell is outlined in black,and the high-symmetry stacking regions of AA,AB and DW are illustrated);(d)—(f) the interlayer spacing of TBG with (d) θ=1.05°,(e) θ=0.53° and (f) θ=0.35°.

為進一步展示晶格弛豫對魔角體系電學性質的影響,利用緊束縛模型計算不同魔角體系的DOS和LDOS.如圖4 所示,晶格弛豫對魔角體系的電子性質有顯著影響.和晶格重構強度的變化規(guī)律類似,隨著角度減小,晶格弛豫對電子性質的影響越發(fā)明顯.首先,我們研究晶格弛豫對DOS 的影響.對于第一魔角,如圖4(a)所示,晶格弛豫導致費米面附近出現孤立的平帶,打開的帶隙值約為42 meV.對比非弛豫結構和弛豫結構在費米面附近的DOS 分布,發(fā)現晶格弛豫沒有明顯改變平帶能量態(tài)密度.理論上講,若第一魔角是θ=1.05°,則第二魔角出現在θ=1.05°/2=0.53°附近.隨后計算了轉角θ=0.53°體系的DOS (圖4(d)),發(fā)現在非弛豫情況下,費米面附近出現了兩個特征峰.體系弛豫后,費米面附近只存在一個峰,且峰的高度明顯降低.而第三魔角弛豫后的體系在費米面附近出現了一系列特征峰.同時,高階魔角體系的能量態(tài)密度中沒有出現能隙,說明這些低能部分的平帶都不是孤立的,這一現象與第一魔角截然不同.以上結果表明,隨著旋轉角度減小,體系電子性質受晶格弛豫影響會越發(fā)顯著.

接下來,考慮不同魔角體系中,晶格弛豫對AA,AB和DW三種高對稱區(qū)域LDOS 的影響.在魔角體系中,不同區(qū)域電子密度分布有顯著不同.例如,費米面附近的電子態(tài)主要局域在AA區(qū)域,只有少部分分布在疇壁上.對于高階魔角的理想結構(非弛豫),AA區(qū)域態(tài)密度在高能部分出現一系列特征峰.但是,在弛豫結構中,這些高能量的峰態(tài)幾乎消失,說明晶格弛豫減小了AA區(qū)域態(tài)密度對體系總態(tài)密度的貢獻.這些特征峰可以通過計算態(tài)密度在實空間的分布來進一步證實.圖4(b)和圖4(c)是不同特征峰電子態(tài)在實空間的分布.可以明顯發(fā)現,費米面附近平帶的電子態(tài)主要局域在AA區(qū)域.隨著角度減小,AA區(qū)域局域電子態(tài)面積逐漸減小,且晶格弛豫會進一步減小電子態(tài)局域面積.對比非弛豫結構和弛豫結構的結果可看出,晶格弛豫對電子態(tài)在實空間的分布有極大的影響.以上計算結果說明晶格弛豫對高階魔角的晶格構型和電學性質有更顯著的影響,這可能是實驗中仍未發(fā)現高階魔角超導特性的原因.

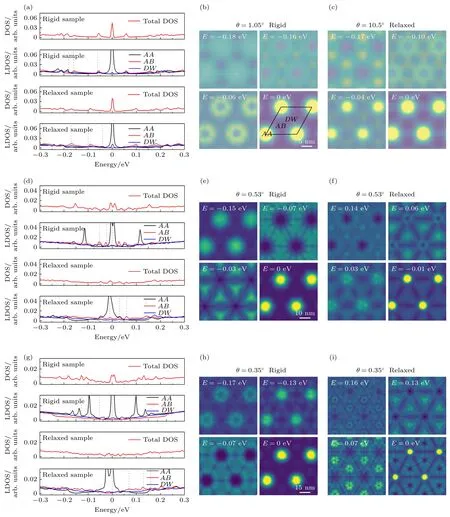
圖4 (a),(d),(g) 三類魔角的DOS 分布;(b),(e),(h) 三類魔角非弛豫體系中不同能量下LDOS 在實空間的分布;(c),(f),(i) 三類魔角弛豫體系中不同能量下LDOS 在實空間的分布.其中(a)—(c) θ=1.05°;(d)—(f) θ=0.53°;(g)—(i)θ=0.35°Fig.4.(a),(d),(g) DOS distributions of three types of magic angles;(b),(e),(h) LDOS distributions in real space at different energies in non-relaxation systems of three types of magic angle non-relaxation systems;(c),(f),(i) LDOS distributions in real space at different energies in relaxation systems of three types of magic angle.The rotation angle θ is 1.05° (a)—(c),0.53° (d)—(f),0.35°(g)—(i).

3.2 tTLG 莫爾超晶格

實驗和理論研究發(fā)現,除TBG 之外,ABC堆垛三層石墨烯[54-57]、tTLG[58-61]、雙層-雙層旋轉石墨烯[62,63]等結構同樣能在石墨烯體系中引入平帶,并且對這些平帶體系的研究中也發(fā)現了各種新奇的量子物態(tài).這一部分將重點介紹tTLG 的平帶以及這一平帶體系中觀察到的強關聯量子物態(tài).相比于TBG,tTLG 擁有更多可調節(jié)的自由度.首先,tTLG 有多種初始結構,例如AAA堆垛、AAB堆垛、ABA堆垛和ABC堆垛等.其次,tTLG 的性質可由兩個獨立旋轉角度θ1和θ2進行調控,其中θ1是第一層和第二層之間的旋轉角度,θ2是第二層和第三層之間的角度.Wu 等[64]研究了不同初始結構的tTLG,發(fā)現初始構型和旋轉層的選取對其電學性質影響顯著,并在A?A(初始結構是AAA堆垛,旋轉中間層)和?AB(初始結構是AAB堆垛,旋轉第一層) 兩種構型中觀察到了平坦能帶.Carr等[58]采用低能有效模型對tTLG-A?A這種垂直鏡對稱性“三明治”結構進行研究,在低能部分發(fā)現平帶和狄拉克錐共存的現象.Park 等[65]發(fā)現tTLG-A?A具備超導性能,當中間層相對于其他兩層以一定角度旋轉時,其超導性比雙層結構更穩(wěn)定.同時Cao 等[66]研究了這種超導現象的自旋特性,發(fā)現在高達10 T 的磁場下體系仍表現出超導性,是一種自旋三重態(tài).Hao 等[67]以“魔角”依次旋轉每層石墨烯來構建tTLG-A?A結構,觀察到具有位移場可調諧的超導性,其超導轉變溫度是2.1 K.值得一提的是,與傳統(tǒng)的超導材料不同,tTLG 中的超導性不是由常規(guī)的弱耦合Bardeen-Cooper-Schrieffer (BCS) 電子對機理引起的,而是強烈依賴于電子的強耦合.Zhang 等[68]研究了tTLG 的超莫爾晶格結構 (θ1=θ2),發(fā)現體系在極低的電子密度(低于兩個數量級)下仍表現出超導的傳輸特性.Turkei 等[69]使用STM 直接表征魔角tTLG-A?A的電子結構,觀察到體系具有基于莫爾晶格的強烈重構,引入了一系列局部扭轉角斷層.在非鏡像對稱堆疊結構中,例如tTLG-?AB,研究者觀察到了非對稱的關聯絕緣態(tài)、鐵磁態(tài)和類似超導的跡象[8,70,71].隨后,研究tTLG-A?A和tTLG-?AB兩種構型中晶格弛豫對平帶的影響.

如圖5(a)所示,tTLG-A?A構型的魔角θ=1.35°(tTLG-A?A-1.35 體系),是TBG 的倍[64].晶格弛豫后,體系仍保持雙重旋轉對稱性C2z.在AAA區(qū)域,上層和下層的原子分別往面外移動.從圖5(d) DOS 分布可以看出,弛豫的體系在費米面附近打開能隙,能隙值約為55.4 meV.平帶的電子態(tài)主要分布在AAA區(qū)域(圖5(e)和圖5(f)),且中間層的DOS 大于外層.tTLG-?AB可以看成由兩部分組成,下層是AB堆垛型雙層石墨烯,上層是相對于下層有一個轉角的單層石墨烯.因此,第一層原子在AAB區(qū)域的z方向位移最大.相比于tTLG-A?A結構,原子在z方向位移均有所減小.tTLG-?AB的魔角θ=1.05°(tTLG-?AB-1.05 體系),與TBG 的魔角一致.晶格弛豫后,體系在費米面附近打開能隙,約23.4 meV.從圖5(g)可以看出,晶格弛豫使平帶對應的DOS 降低.平帶的電子態(tài)主要分布在AAB堆垛的上層和中間層.以上結果表明,在tTLG 中,晶格弛豫對由不同初始結構和不同旋轉層構成體系的晶格結構和電子性質有不同的影響.

圖5 (a) tTLG-A?A-6.01 體系的側視圖(上)和俯視圖(下);(b),(c) 分別為tTLG-A?A-1.35 體系和tTLG-?AB-1.05 體系中原子在z 方向的位移Δz;(d)—(f) tTLG-A?A-1.35 體系中DOS (d)和不同能量點LDOS (e),(f)在實空間的分布;(g)—(i) tTLG?AB-1.05 體系中DOS (g)和不同能量點LDOS (h),(i)在實空間的分布[64]Fig.5.(a) Side (upper) and top (lower) views of tTLG-A?A-6.01;(b),(c) the displacement Δz of atoms in the z direction for tTLG-A?A-1.35 and tTLG-?AB-1.05,respectively;(d)—(f) distribution of DOS (d) and LDOS at different energy points in real space (e),(f) of tTLG-A?A-1.35.(g)—(i) distribution of DOS (g) and LDOS at different energy points in real space (h),(i) of tTLG?AB-1.05[64].

目前一些研究表明,壓強是調節(jié)旋轉石墨烯性質的一種有效手段.Yankowitz 等[10]通過靜水壓力改變層間間距,在旋轉角度為θ=1.27°的TBG中誘導超導態(tài),觀察到最大超導轉變溫度Tc約3 K.這里,通過具體計算闡述外部壓強對tTLG 物性的調控作用.如圖6(b)所示,tTLG-A?A-1.89本身不存在平帶,且費米面附近電子態(tài)主要分布在中間層[72].當對體系施加4 GPa 的壓強,增強的層間相互作用使每一層費米面附近的電子態(tài)向AAA區(qū)域聚集,從而誘導產生新的平帶.但是晶格弛豫后,體系只打開6 meV 的能隙,遠遠小于tTLG-A?A-1.35 的能隙.這個區(qū)別可由晶格弛豫后體系結構的不同重構來解釋.如圖6(c)所示,在4 GPa 壓強下,晶格弛豫并未改變原子在z方向的分量,仍類似于非弛豫結構,使得AA堆垛與AB堆垛的層間距相同,AA區(qū)域的層間相互作用ω0接近于AB的層間相互作用ω1.而對于tTLG-A?A-1.35,ω1/ω0比值遠大于1.能隙的大小決定于ω1與ω0的相對大小,具體來說,正比于ω1/ω0.因此,圖6(d)中tTLG-A?A-1.89 加壓后的能隙遠小于tTLG-A?A-1.35 的能隙.對于旋轉角度為1.89°的TBG,誘導產生平帶所需的強壓約為9 GPa,約為tTLG 的兩倍[73].上述結果進一步表明tTLG 相對于TBG 具有更加可調的晶體結構和電子性質.

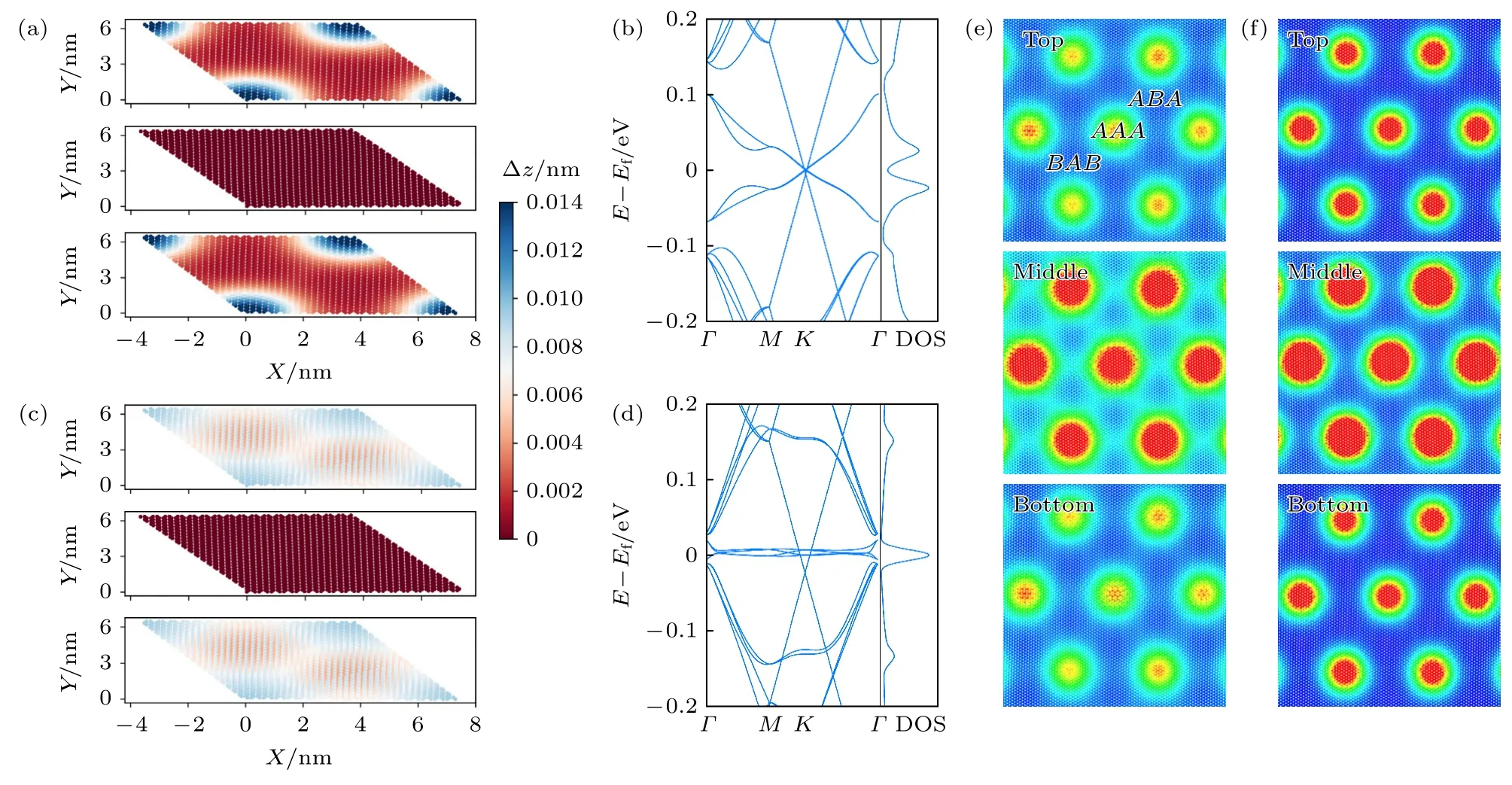
圖6 (a),(c) tTLG-A?A-1.89 體系分別在常壓和4 GPa 高壓條件下原子在z 方向的位移Δz;(b),(e) 體系在常壓條件下的能帶、DOS (b)和范霍夫奇點處LDOS 在實空間的分布(e);(d),(f) 體系在4 GPa 高壓條件下的能帶、DOS (d)和范霍夫奇點處LDOS 在實空間的分布(f)[72]Fig.6.(a),(c) Out-of-plane displacement Δz of relaxed tTLG-A?A-1.89 without and with 4 GPa vertical pressure,respectively;(b),(e) the band structure,DOS (b) and LDOS mappings of van Hove singularities (e) of tTLG-A?A-1.89 under ambient pressure;(d),(f) the band structure,DOS (d) and LDOS mappings of van Hove singularities (f) of tTLG-A?A-1.89 with 4 GPa pressure[72].

4 石墨烯-hBN 異質結構中的自發(fā)弛豫

石墨烯上具有很多優(yōu)異性能,其應用的難點之一是高效地制備出高質量樣品.早期石墨烯的生長制備主要在SiO2襯底表面,但是由于其平整度不高,制備的石墨烯樣品會出現褶皺[74].金屬襯底上制備的石墨烯樣品具有優(yōu)異的力學性能,但石墨烯低能部分的電子態(tài)會與襯底的金屬態(tài)發(fā)生雜化,從而影響樣品的電子結構[75].2010 年Dean 等[76]在hBN 襯底上制備了石墨烯樣品,顯著提高了樣品的力學和電學性能.hBN 的晶體結構與石墨烯類似,主要不同是hBN 由氮原子和硼原子分別占據一個子晶格構成,這種結構使其具有跟石墨烯完全不同的電子性質.hBN 具有原子級平整的表面,是一種絕緣體材料,具有較大的能隙,沒有懸掛鍵,光學聲子的能量較高,是目前制備高質量石墨烯樣品常用的襯底.

隨后,研究者發(fā)現石墨烯和hBN 會以范德瓦耳斯力堆垛形成異質結,其電子性質與二者之間的旋轉角度密切相關.當旋轉角度小于2°,石墨烯表面會形成較大周期的莫爾條紋[77-79].莫爾條紋可以視為施加在石墨烯上的周期勢,可對石墨烯的能帶進行調控.如在對石墨烯/hBN 異質結輸運性質的研究中,研究者發(fā)現了其莫爾超晶格能級隨著外界磁場的變化形成分形結構,實現了Hofstadter 提出的“霍夫斯塔特蝴蝶”(Hofstadter’s butterfly)能譜[80-83].氮化硼襯底對單層石墨烯的性質調控主要有: 1) 在石墨烯狄拉克點打開一個能隙;2) 在較高能量形成一系列超晶格狄拉克點.超晶格狄拉克點的出現源于石墨烯上的莫爾超晶格勢,而石墨烯同hBN 之間旋轉角度越小,超晶格狄拉克點同石墨烯狄拉克點的距離越近.氮化硼/石墨烯/氮化硼形成的超莫爾三明治結構中同樣存在超晶格狄拉克點[84-87].

hBN 的兩個子晶格分別由兩種類型的原子占據,當石墨烯與hBN 的晶向基本一致時,理論上可以通過hBN 的兩個子晶格來調節(jié)石墨烯子晶格的占位能,從而打破石墨烯平面內的反演對稱性,進而打開石墨烯的能隙.同時氮化硼襯底會使石墨烯發(fā)生晶格重構,可進一步提高能隙值[88].目前報道的石墨烯/氮化硼莫爾超晶格(石墨烯與氮化硼晶向一致)的能隙,不同的實驗測量得到的數值并不一致.例如,輸運測試中觀察到的帶隙值范圍是10—30 meV[82];磁光譜測得帶隙值約為40 meV[89];角分辨光電子能譜測得的帶隙值是160 meV[90];光電流譜測得的帶隙值是14 meV[91];而理論預測的能隙值范圍是2—14 meV[77,78,92].更有趣的是,當魔角雙層石墨烯與氮化硼對齊時,體系中出現本征QAH 效應[13].這里可能是因為強相互作用將電子極化為具有單自旋/能谷分辨的孤立小能帶,每個小能帶都有非零的陳數,從而驅動了QAH 效應的產生[93,94].同時,氮化硼襯底會影響魔角石墨烯中的超導態(tài)[21,95].綜上所述,當石墨烯與氮化硼晶向一致時,襯底對石墨烯體系的晶體結構和電子性質產生了顯著的影響.

石墨烯與氮化硼的晶格結構存在1.7%的晶格失配,可形成的最大莫爾條紋長度約為14 nm,對應的晶胞包含12322 個原子.大多數理論研究都是從低能有效模型出發(fā),將襯底的效應以莫爾超晶格勢的形式加入石墨烯的哈密頓量中,忽略了晶格弛豫對體系的影響[77,78],或只考慮面外原子位移的變化[88].低能有效模型可以有效解釋部分實驗現象,但是模型過于簡單,不能考慮原子真實的形變.接下來,我們結合半經典分子動力學和緊束縛模型,系統(tǒng)地闡述氮化硼襯底對單層石墨烯和魔角石墨烯晶格結構和電子性質的影響.

4.1 單層石墨烯-hBN 異質結構

2015 年,Slotman 等[41]利用分子動力學模擬軟件LAMMPS[51]對超晶格進行晶格弛豫,石墨烯層內相互作用采用經驗鍵序作用勢[96],層間相互作用采用Kolmogorov-Crespi 勢.對于石墨烯中碳原子與hBN 中氮原子和硼原子間相互作用,仍用Kolmogorov-Crespi 勢,但C—B 和C—N 之間相互作用分別是C—C 的0.6 倍和2 倍[41].為了模擬塊體襯底,hBN 原子結構保持不變.晶格弛豫會在體系中引入形變標勢VD和矢勢A,這些效應都可以加入石墨烯緊束縛模型的哈密頓量中[16].矢勢A通過Slater-Koster 近似改變原子間的躍遷振幅,標勢VD以占位能的形式加入,其表達式是

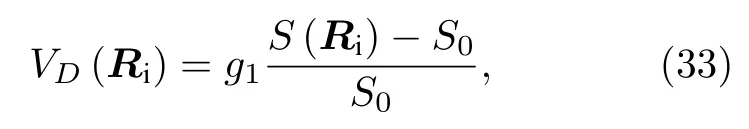
其中,S(Ri)是晶格弛豫后Ri位置處原子的有效面積,S0=是非弛豫結構中碳原子的有效面積,g1=4 eV 是石墨烯中屏蔽引入的形變勢[97].

圖7(a)和圖7(b)展示了轉角為θ=0°的石墨烯與氮化硼超晶格體系在結構弛豫后修正的緊束縛模型參數.隨后,利用緊束縛傳播方法計算體系的DOS 和準本征態(tài)在實空間的分布情況.在此部分計算中,體系哈密頓矩陣(20)式只考慮碳原子的躍遷能和占位能.如圖7(c)和圖7(d)所示,對于轉角θ=0°的體系,晶格弛豫后,導帶和價帶都出現了超晶格導致的新的狄拉克錐,這與實驗結果相符合[80-82,98,99].超晶格狄拉克點的位置取決于莫爾超晶格的倒格矢G,由ED=給出,其中vF為費米速度[100,101].因為倒格矢長度取決于θ,超晶格狄拉克點的位置會隨轉角θ而變化(圖7(d)).結構弛豫效應會隨θ的增加而減小,這意味著對于較大θ,超晶格狄拉克錐會消失.

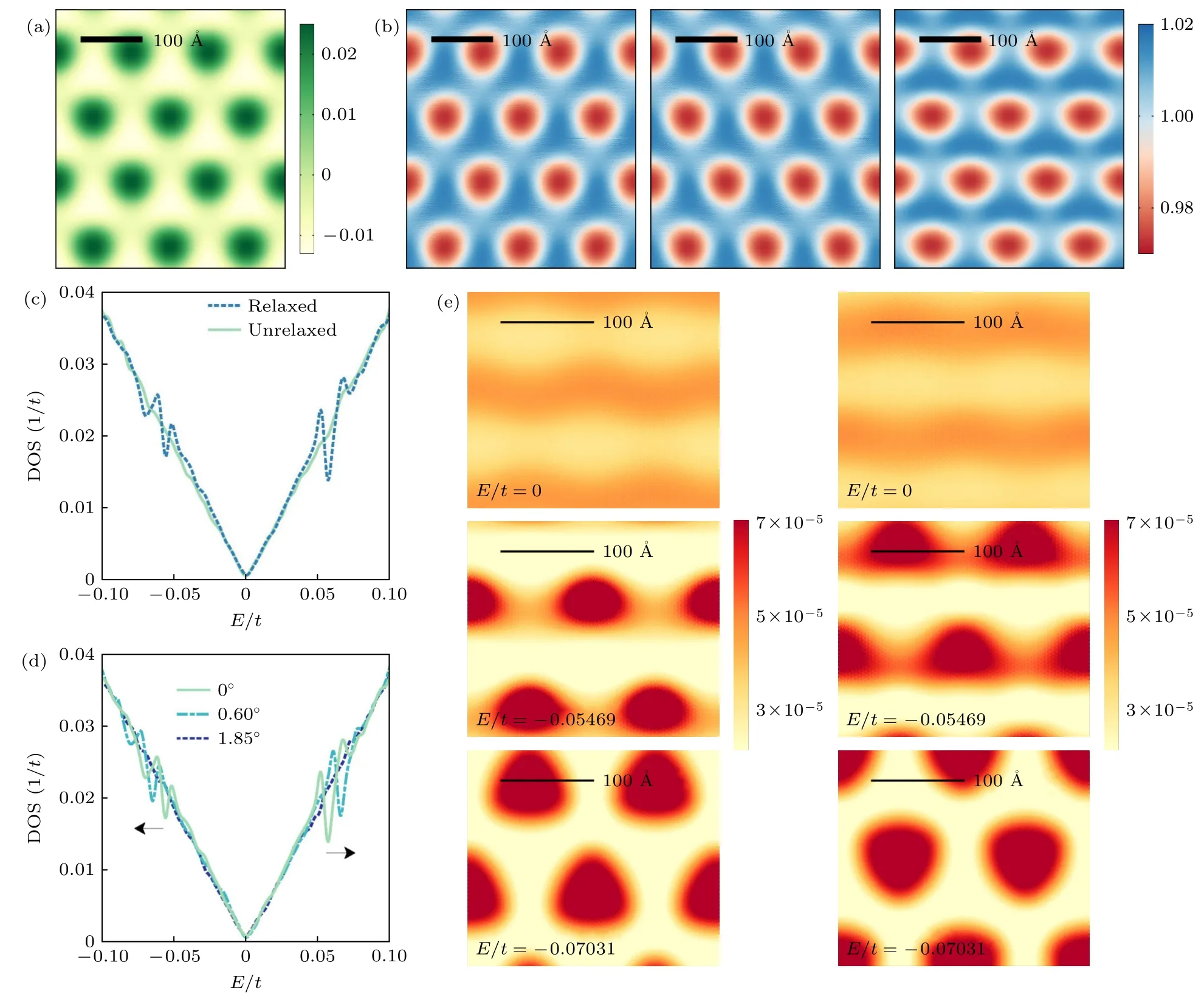
圖7 (a),(b) 石墨烯/氮化硼之間轉角 θ=0° 的體系在晶格弛豫后的緊束縛模型參數(λ=13.8 nm;從左到右分別為在位能VD和碳原子最近鄰的躍遷振幅t1,t2,t3,彩色條的單位是t=2.7 eV);(c) 非弛豫和弛豫結構石墨烯的DOS 分布;(d) 不同 θ 下的DOS (箭頭表示超晶格狄拉克點隨轉角的減小而向高能部分移動;當 θ=1.85°,超晶格狄拉克點消失;相應的莫爾長度分別為 λ=13.8,11.9,6.7 nm);(e) 轉角 θ=0° 時不同能量下的準本征態(tài)在實空間的分布 (左側和右側分別是A 子晶格和B 子晶格的準本征態(tài);對于接近超晶格狄拉克點的能量,可以形成一個清晰的莫爾條紋[41])Fig.7.(a),(b) Modified tight-binding parameters for a relaxed sample of graphene on hBN with θ=0° (λ=13.8 nm;from left to right,the on-site potential VD and the hopping parameters t1,t2,and t3.The color bars are in units of t=2.7 eV);(c) DOS distributions of unrelaxed and relaxed graphene;(d) DOS for different angles θ (As indicated by the arrows,superlattice Dirac point moves towards the high-energy part with the decreasing of the turning angle;the superlattice Dirac point disappears at θ=1.85° .The corresponding moiré lengths λ=13.8,11.9,6.7 nm,respectively);(e) amplitude of the quasi eigenstates for different energies in real space for θ=0° (The left-hand panels show sublattice A and the right-hand panels show sublattice B.For energies closer to the extra Dirac cones,a clear moiré pattern can be distinguished)[41].

圖7(e)展示了不同能量準本征態(tài)在實空間的振幅分布.由于hBN 襯底打破了石墨烯子晶格的子晶格對稱性,我們將兩套子晶格的振幅分布分別繪制.如圖7(e)所示,當準本征態(tài)遠離費米能量時,出現了空間局域性.對于能量接近費米能量的準本征態(tài),空間幅度的分布差異很小.而對于能量更接近超晶格狄拉克點的準本征態(tài),空間分布表現出清晰的莫爾條紋.DOS 中超晶格狄拉克點的出現和準本征態(tài)中的空間局域性特征表明單層石墨烯/hBN 的電子結構受到了結構弛豫的強烈影響.石墨烯在hBN 襯底上的直流電導率的實驗測量結果[80-82]表明,在空穴側和電子側的超晶格狄拉克點處,電導率出現不對稱的下降.空穴側電導率的降低更為顯著,其值甚至低于狄拉克點的最小電導率[80].

4.2 TBG-hBN 莫爾超晶格

為進一步研究氮化硼襯底對TBG 晶體結構和電學性質的影響,我們考慮TBG/hBN 和hBN/TBG/hBN 兩大類體系,并采用類似于石墨烯/hBN的勢參數對體系進行晶格弛豫[102].同時,在緊束縛模型(21)式中加入氮化硼貢獻的躍遷能和占位能,其中硼原子、氮原子和碳原子的占位能分別是VB=3.34 eV,VN=-1.4 eV 和VC=0,躍遷能由Slater-Koster 近似確定[77].

對于TBG/hBN 結構,如圖8 所示,當下層石墨烯與氮化硼襯底夾角小于2°時,襯底會顯著改變體系的晶體結構和電子性質[102].隨著轉角θbot增大,AAA堆垛區(qū)域的渦旋狀由三角形變?yōu)閳A形.晶格弛豫使下層石墨烯在ABC區(qū)域產生最大值約為60 meV 的形變勢能,在AAA區(qū)域產生最大值為18 T 的贗磁場.而上層石墨烯的形變勢能和贗磁場值都要小一個數量級.因此,在低能有效模型中通過在相鄰石墨烯中引入有效周期勢來考慮hBN襯底對TBG 的影響是合理的[103-105].TBG/hBN哈密頓矩陣的占位能來自于兩部分的貢獻: 第一部分是氮原子和硼原子的占位能之差,這種貢獻打破石墨烯平面內的反演對稱性,是體系能隙的主要來源;第二部分是由晶格弛豫引起的形變勢能,導致相鄰子晶格的勢能差,會在體系局部產生能隙,對體系能帶有微調作用.作用于K谷的贗磁場方向與K′谷相反,因此贗磁場沒有打破體系的時間反演對稱性.

如圖8(d)—(f),隨著θbot的增大,hBN 襯底對TBG 能帶影響減小,在θbot接近3°時,平帶之間仍打開能隙.當θbot=0.53°時,能隙值約為25—30 meV.對于無襯底的TBG,層自由度、自旋和谷自由度沒有相互耦合,費米面附近的平帶具有八重簡并.在TBG/hBN 體系中,hBN 襯底對下層石墨烯的影響更大,打破TBG 的層簡并度.同時,上層K谷映射到下層K′谷,如圖8(d)所示,帶邊的平帶出現分裂.不同谷的能帶可通過谷算子[106]來分辨:

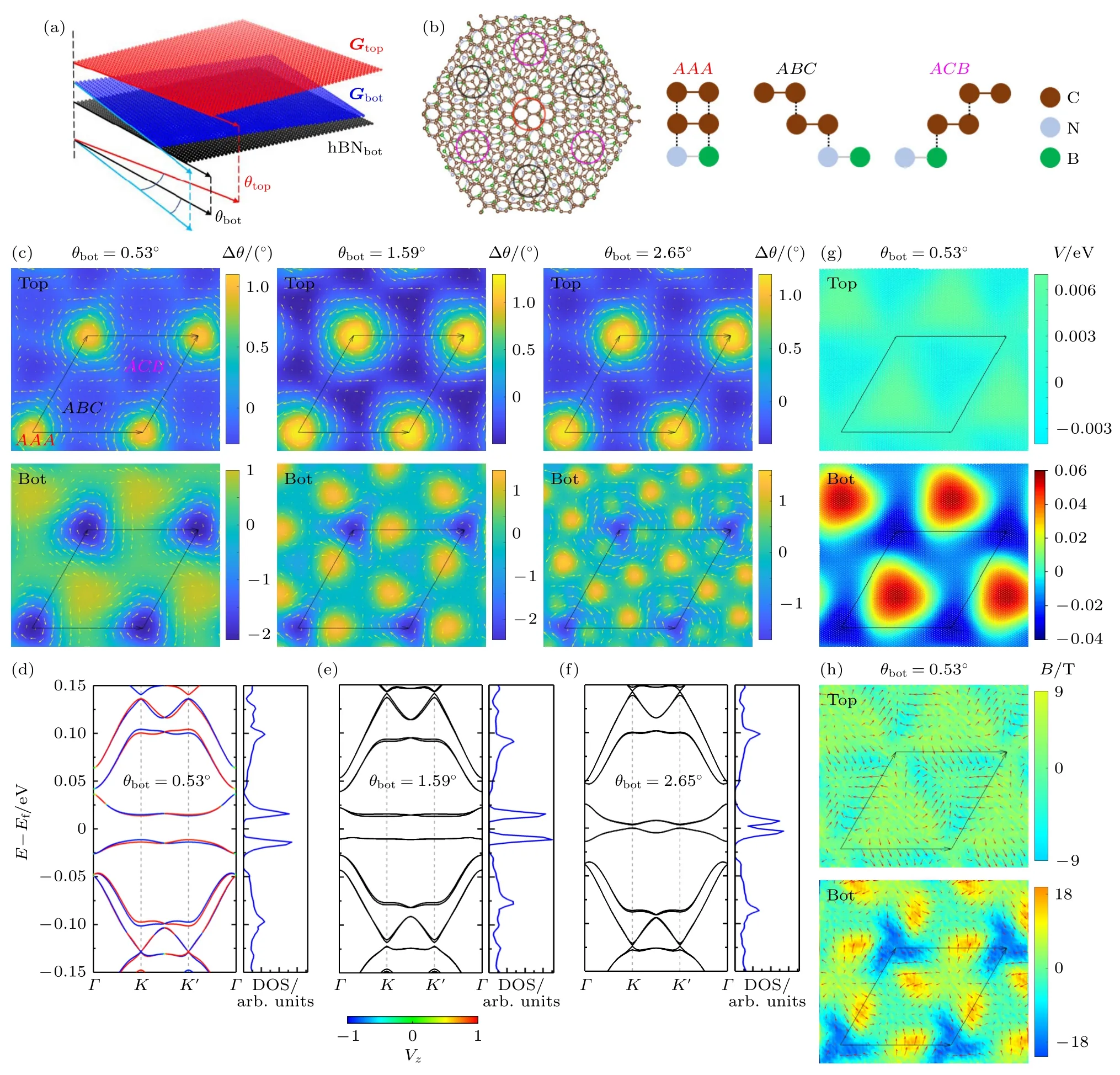
圖8 (a) TBG/hBN 的結構示意圖;(b) TBG/hBN 的俯視圖和高對稱堆垛結構;(c) 不同 θbot 體系的面內形變u(r)和面內轉角Δθ=?×u,白色箭頭是原子的面內位移;(d)—(f) 不同 θbot 體系的能帶圖和DOS (彩色條表示每個谷的帶,如果屬于K 谷狀態(tài)(紅色),則 ≈1,如果屬于K′谷狀態(tài)(藍色),則≈-1);(g),(h) 晶格重構引起的形變勢能 VD 與贗磁場B=?×A (紅色箭頭代表矢勢A(r),TBG 的轉角固定為 1.05° [102])Fig.8.(a) Schematic of the atomic configuration of TBG/hBN;(b) top view and high-symmetry stacking regions of the atomic configuration of TBG/hBN;(c) in-plane strain u(r) and in-plane rotation angle Δθ=?×u with varying θbot (The in-plane displacements are visualized with white arrows);(d)—(f) band structure and DOS of TBG/hBN with different θbot (The color bar denotes the band for each valley with ≈1 if a state belongs to valley K and ≈-1 if a state belongs to valley K′);(g) the deformation potential VD and (h) pseudo-magnetic field B=?×A induced by lattice relaxations in the TBG/hBN with θbot=0.53°(The vector field A(r) is visualized with red arrows in (h) TBG is fixed to θtbg=1.05° in all cases)[102].

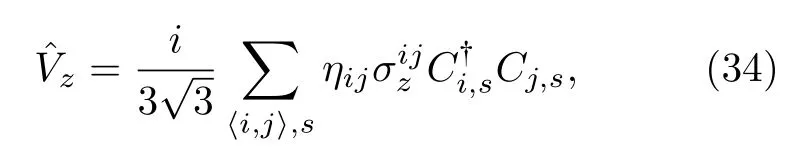
其中i,j表示對次近鄰位點求和;ηij=±1 分別表示順時針和逆時針躍遷;是定義在子晶格自由度的泡利矩陣.谷算子的期望值范圍從1 到 —1,分別對應K和K′谷.

接著在TBG/hBN 異質結表面再加另外一層氮化硼形成三明治結構,如圖9(a)所示,hBN/TBG/hBN 體系中引入一個新的自由度θtop[102].當θtop=θbot時,上層和下層hBN 晶格結構對齊,體系中的平帶打開約50 meV 能隙,對應贗磁場最大值約為36 T,同時,體系恢復八重簡并.由圖9 可以明顯看出,三明治結構的電學性質對hBN 旋轉角度高度敏感.

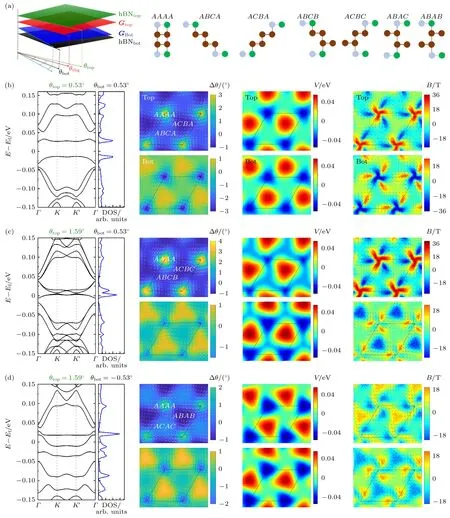
圖9 (a) 三明治結構hBN/TBG/hBN 的形貌圖和高對稱堆垛結構;(b)—(d) 不同 θtop 和 θbot 組成體系的(從左到右)能帶圖、面內轉角、形變勢能和贗磁場 (TBG 的轉角固定為 θtbg=1.05°)[102]Fig.9.(a) Schematic structure of the hBN/TBG/hBN system and the different high-symmetry stackings in the superlattice;(b)—(d) panels from left to right display the band structure,in-plane twist of the atoms with respect to their original position,scalar potential and pseudo-magnetic field of the systems with different θtop and θbot (TBG is fixed to 1.05°[102]).

5 總結與展望

目前,石墨烯莫爾超晶格的實驗和理論研究已取得一系列進展,出現了很多新奇現象,但還需要大量工作來揭示其背后的物理機制.例如在實驗和理論上,需要更加深入探究魔角石墨烯體系中超導和關聯絕緣態(tài)的機制.高階魔角體系中是否存在類似于第一魔角體系的物理現象? 旋轉多層石墨烯體系中是否有更豐富、更新的新奇性質? 此外,其他二維材料(如過渡金屬硫族化合物、氮化硼和黑磷等[2]) 所組成的莫爾超晶格引起了廣泛關注.如實驗和理論已在過渡金屬硫族化合物莫爾超晶格中發(fā)現了平坦能帶[107-109],并觀測到關聯絕緣態(tài)[110]、QAH 效應[111]、連續(xù)金屬絕緣體轉變[112]、奇異金屬態(tài)[113]和鐵電疇[114]等.相對于石墨烯構成的異質結,其他二維材料的莫爾超晶格研究正處于起步階段,期待出現更多新奇現象.與此同時,晶格弛豫和襯底效應將會對其他二維材料的莫爾超晶格產生重要影響,需要更多實驗和理論研究去闡明相關的物理類機制.