雙層石墨烯中的偶數分母分數量子霍爾態*
李慶鑫 黃焱 陳以威 朱雨劍 朱旺 宋珺威 安冬冬 甘祺康 王開元 王浩林? 麥志洪Andy Shen 郗傳英 張警蕾 于葛亮? 王雷??
1) (南京大學物理學院,固體微結構物理國家重點實驗室,南京 210093)
2) (南京大學,人工微結構科學與技術協同創新中心,南京 210093)
3) (中國科學院強磁場科學中心,合肥 230031)
4) (湖北九峰山實驗室,武漢 430206)
在半填充的朗道能級,復合費米子手征p 波配對的Moore-Read 態具有e/4 的分數激發,其中部分這種準粒子服從非阿貝爾統計,有望用于實現拓撲量子計算.雙層石墨烯由于其電子的SU(4)對稱性和電場對其性質的方便調控性,成為研究多分量量子霍爾態的理想平臺,是實現非阿貝爾統計的候選者.本文利用干法轉移技術制備了雙層石墨烯/氮化硼異質結,通過電學輸運測量展示了雙層石墨烯在調節外電場和磁場下的量子霍爾態行為.在強磁場下,觀測到了朗道能級填充因子為—5/2,—1/2,3/2 的伴隨著量子化霍爾電導的不可壓縮態.隨著磁場繼續增強,這些偶數分母量子霍爾態特征先增強再減弱,對應朗道能級波函數的極化.實驗結果暗示觀察到的這些偶數分母分數量子霍爾態屬于由Pffafian 波函數描述的拓撲態.
1 引言
二維電子系統中的多體關聯與非平庸拓撲導致了許多新奇的現象,例如分數量子霍爾效應(fractional quantum Hall effect,FQHE)[1].在強磁場下,高簡并度的朗道能級形成幾乎零色散的平帶,增強的庫侖作用(U~,磁長度lB=,h是普朗克常數,e是元電荷,B是磁感應強度)與規范不變性共同作用使電子與磁通形成復合費米子[2,3],表現出分數量子化的霍爾電導.當朗道能級被半填充時,復合費米子感受到的有效磁場變為零,從而形成可壓縮的復合費米子液體[4].這種費米液體同樣可能在復合費米子庫珀配對下失穩,被預言形成類似拓撲超導的Moore-Read 態,其激發是遵循非阿貝爾統計的馬約拉納模式[5,6].
在GaAs 量子阱朗道能級ν=5/2 處[7,8],人們首次觀測到半填充處的FQHE,但一些實驗結果與預言的Moore-Read 態行為并不完全一致[9-11],仍缺乏支持非阿貝爾統計的直接證據.最近在單層石墨烯N=0 朗道能級[12]與更高的朗道能級[13]中同樣出現了半填充處的不可壓縮態,而后者被解釋為可能的非阿貝爾態.與GaAs 體系不同,石墨烯中的低能電子具有自旋和能谷簡并構成的SU(4)對稱性[14],其朗道能級由多分量波函數描述.在部分填充的朗道能級,這些自由度的交換能與塞曼能對決定石墨烯的量子霍爾行為非常重要[15].然而單層石墨烯中的狄拉克點受C2z對稱性保護,谷間帶隙無法被外界打開,這大大限制了人們對單層石墨烯中量子霍爾態的調控能力.雙層石墨烯中,由于缺少C2z對稱性,可以通過調節垂直電場來控制兩個能谷間的能量差從而方便地調控量子霍爾態到可壓縮態的轉變[16-18],同時利用磁場適當地調節軌道波函數結構,雙層石墨烯中有可能出現Moore-Read 態[19-21].之前有相關報道用電容設備測量并展示了雙層石墨烯中的偶數分母分數量子霍爾態,但是由于測量方法的限制并沒有能得到像電輸運一樣能反映橫向電導平臺的數據[22].最近也有研究者在六方氮化硼封裝的雙層石墨烯中用電輸運的方法測到了一系列偶數分母分數量子霍爾態[23],但是在高于31 T 的強磁場下卻缺乏相關的研究,而一直以來偶數分母分數量子霍爾態在高場下的變化趨勢為猜測其是Pfaffian 或anti-Pfaffian 態的一個重要依據,因此十分重要[20].本文制備了高質量的雙層石墨烯雙柵器件,通過使用少層石墨代替傳統的合金接觸,獲得了原子級平整的接觸電極.在強磁場下,施加一定的電位移場調節谷塞曼能,觀測到了一系列魯棒的偶數分母分數量子霍爾態,為未來進行干涉實驗檢驗非阿貝爾統計性質提供了研究平臺.
2 實驗與討論
圖1(a)展示了器件的結構示意圖,通過“拾取法”轉移法[24]拾取六方氮化硼對雙層石墨烯進行封裝,這不僅為雙層石墨烯提供了平整的襯底還使其隔絕空氣環境,提高了器件遷移率.同時在雙層石墨烯的上下方使用石墨作為柵極,相比于金屬柵極減少了合金蒸鍍時引入的無序和缺陷.另外在雙層石墨烯的兩邊使用少層石墨與雙層石墨烯接觸,再用金屬電極與少層石墨完成邊緣電接觸,極大地降低了接觸電阻,提升了器件的質量.這種范德瓦耳斯層狀結構允許上下柵極的獨立使用,從而可以分別調控雙層石墨烯中的載流子濃度n和電位移場強度D.載流子濃度為n=(CTVT+CBVB)/e-n0,電位移場強度表示為D=(CTVT-CBVB)/2ε0-D0(CT和CB分別為上、下層電介質單位面積的電容,VT和VB分別為上、下層柵極所施加的電壓,n0和D0為剩余載流子濃度和剩余電位移場).圖1(d)給出了T=1.5 K 時,雙層石墨烯器件在電位移場強度D和磁場強度B都為 0 的情況下,縱向電阻Rxx隨載流子濃度n的變化關系.根據狄拉克峰的半峰寬可以估算出器件中缺陷和雜質的量級3.5×1010cm-2,遷移率為106cm2/(V·s).
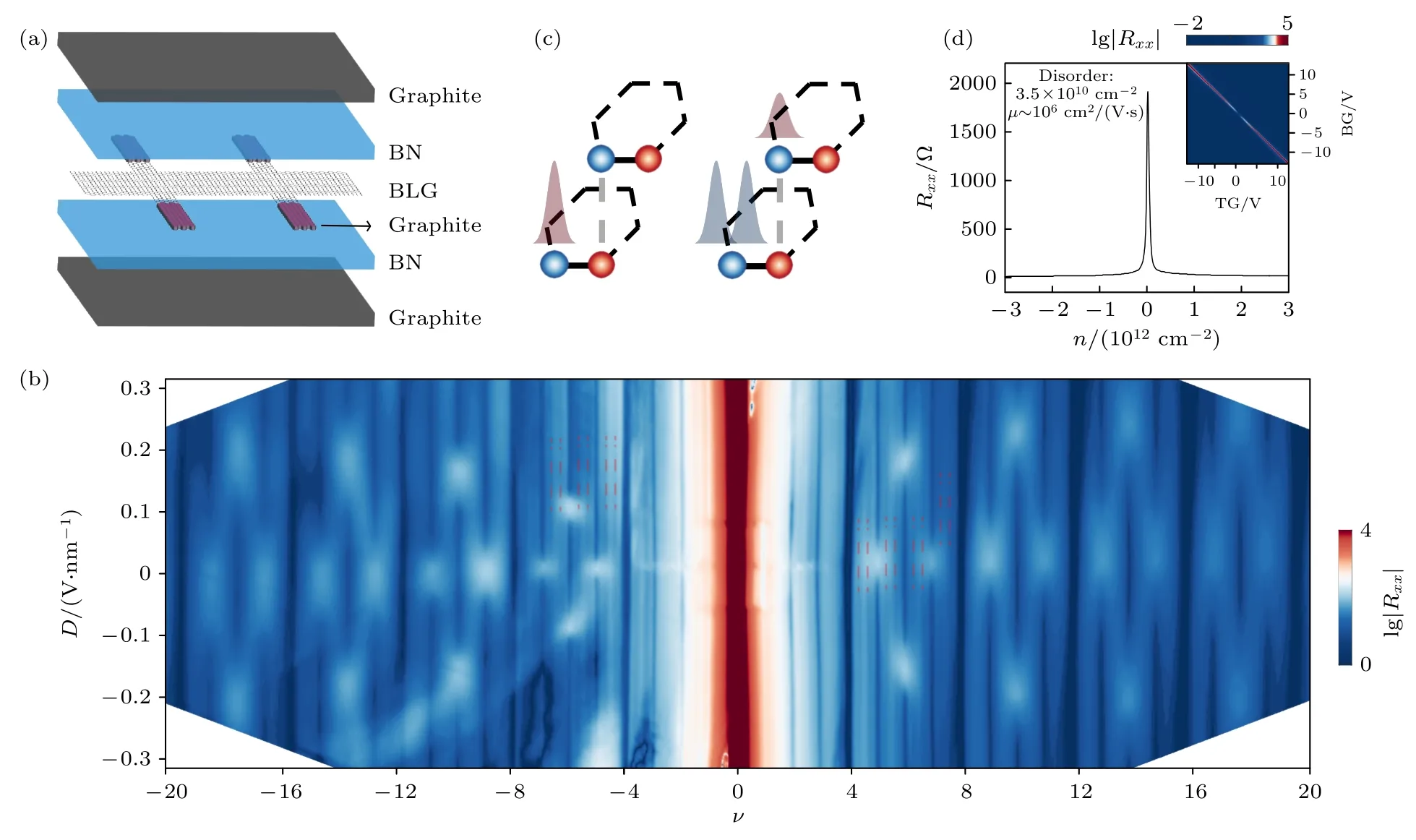
圖1 器件結構和雙層石墨烯里的分數量子霍爾態 (a) 器件結構圖;(b) 溫度T= 1.5 K 與磁場B= 8 T 時,縱向電阻Rxx 隨電位移場D 和填充因子ν 的變化圖(紅色虛線表示以3 為分母的分數態) (c) 雙層石墨烯N=0,1 朗道能級中四原子上波函數分布圖;(d) 溫度T=1.5 K,電位移場D= 0 V/nm 與磁場B= 0 T 時,縱向電阻Rxx 隨載流子濃度n 的變化Fig.1.Device structure and FQH states for in bilayer graphene (BLG): (a) Device schematic;(b) Rxx versus ν and D at B= 8 T and T= 1.5 K (The red dotted lines represent the fractional state with 3 as the denominator);(c) the schematic of wave function distribution on the four atomic sites of BLG for the N=0,1 Landau orbital states;(d) Rxx versus n at D= 0 V/nm,B= 0 T,and T= 1.5 K.
圖1(b)展示了T=1.5 K 時雙層石墨烯器件在固定垂直磁場下(B=8 T)縱向電阻Rxx隨朗道能級填充因子ν(ν=nh/(eB),n是載流子濃度)和電位移場強度D的變化關系.我們觀察到一系列在外場和庫侖相互作用下SU(4)對稱性破缺導致的整數量子霍爾態,對應于縱向電阻Rxx出現極小值.其次,在ν=—7 到—4 之間和ν=4—8 之間,觀察到以3 為分母的分數量子霍爾態(圖1(b)中用紅色虛線標識),這說明器件具有很高的質量.在|v|> 4 范圍內,同一朗道能級中填充因子為奇數的量子霍爾態出現在所有電位移場不為零的區域,而填充因子為偶數的量子霍爾態在有限的電位移場下消失,這是因為電位移場會改變單粒子谷塞曼能導致朗道能級出現交叉[16,17].而在|ν|≤4 區域內,ν=±1 處在D=0 V/nm 與有限大的電位移場時發生了壓縮態與不可壓縮態的轉變;ν=±2處,在電位移場十分接近零時發生相變;ν=±3 處的相變只發生在D=0 V/nm 處,這些現象源于雙層石墨烯特殊的朗道能級結構[18,25].與非狄拉克型色散的二維量子阱(例如GaAs 量子阱)不同,雙層石墨烯的N=0 與N=1 朗道能級是簡并的[26].圖1(c)展示了雙層石墨烯中K谷的零能朗道能級波函數,K′谷的波函數可同時改變層與子格占據位置獲得.其中N=0 軌道等同于非相對論粒子的n=0 朗道能級波函數,而N=1 軌道則是n=0與n=1 波函數的組合.增加磁場不僅會解除軌道的簡并,還會改變N=1 軌道中兩種態的占據權重,特別是,非阿貝爾的 Pfaffian 態被預言出現在n=1 軌道上[5].另外軌道的簡并性在雙層石墨烯中也引入了不可忽略的朗道能級散射,這對穩定可能出現的拓撲相非常重要[19,27,28].
在更高的磁場下,我們在雙層石墨烯中進一步觀測到了更多奇數分母的分數量子霍爾態以及出現在半填充處的分數量子霍爾態(圖2—圖4).圖2(a)展示了當電位移場為D=—0.12 V/nm,填充因子ν=1—2 時,縱向電阻Rxx隨填充因子ν和磁場B變化的二維圖.與圖1(b)相比,可以看到在1+1/5,1+2/5,1+3/7 及其共軛處和1+1/2處出現了一系列新的不可壓縮態.為分析這些分數態,固定磁場在33.75 T,作出了縱向電阻Rxx和橫向電導σxy隨填充因子ν的變化圖(圖2(b)).可以看到在1<ν<2 內,當朗道能級處于上述分數填充時,橫向電導以e2/h為單位產生量子化的平臺,其平臺值為σxy=νe2/h.出現這些特征的分數態大致上可分為兩類: 一類是可以由Jain 波函數描述的復合費米子態.根據復合費米子理論,每個復合費米子由一個電子攜帶2p個量子磁通 (?0=h/e)組成,且這些復合費米子[2]感受到有效磁場為B*=B-2pn?0,形成等效的“朗道能級”,有效填充因子ν*=nh/(eB*),因此這類分數態的填充因子可以描述為ν=1+ν*/(2pν*±1) (1<ν<2),其中p是整數.另一類是復合費米子無法描述的偶數分母分數量子霍爾態(ν=3/2 態),與GaAs 體系中被預測為anti-Pfaffian 態的ν=5/2 態[27,29]不同的是,本文結果表明復合費米子態在3/2 附近是粒子空穴對稱的,并且最近研究報道ν=3/2 這類態可能為Pfaffian 態[22].
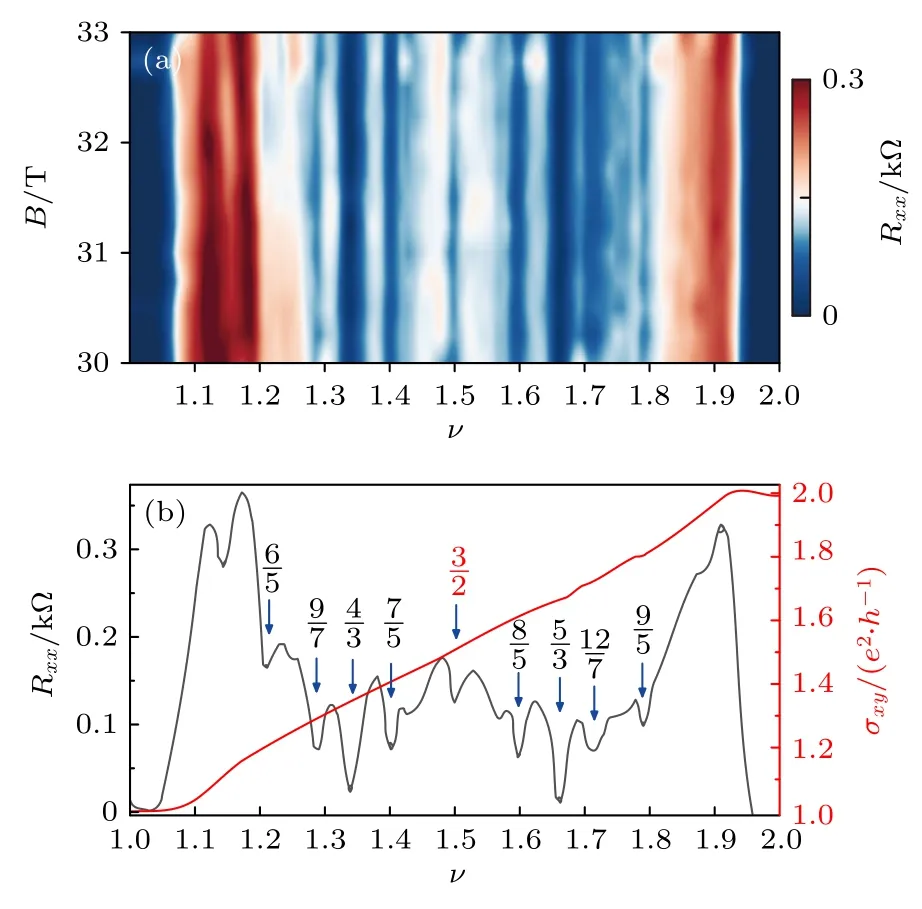
圖2 1 <ν< 2 時的分數量子霍爾態 (a) 溫度T=0.3 K與電位移場D =—0.12 V/nm 時,縱向電阻Rxx 隨填充因子ν 和磁場B 變化的二維圖;(b) 固定溫度T=0.3 K、電位移場D =—0.12 V/nm 與磁場B=33.75 T 時,縱向電阻Rxx (黑色)和橫向電導σxy (紅色)隨ν 的變化Fig.2.FQH states for 1 <ν< 2: (a) Rxx as a function of ν and B at T =0.3 K and D=—0.12 V/nm;(b) Rxx (black)and σxy (red) versus ν at B =33.75 T,D=—0.12 V/nm and T =0.3 K.
圖3 和圖4 分別給出了填充因子—1<ν<0 和—3<ν<—2 時,Rxx隨B和ν變化的二維圖,以及在固定磁場下Rxx和σxy隨ν的變化.在ν<0 時,雖然在—1<ν<0 和—3<ν<—2 的半填充處都出現了明顯的不可壓縮態,對應著Rxx表現為極小值,但是相比ν=—1/2,ν=—5/2 處Rxx下降幅度更小(ν=—5/2 處Rxx下降了80 Ω,而ν=—1/2處Rxx下降了800 多歐姆),因此我們認為出現在ν=—1/2 的不可壓縮態要比出現在ν=—5/2 處的更強,這可能是受朗道能級之間的混合,或是體系的無序和雜質的影響,與之前的報道吻合[23].除此之外,在ν=—12/5,ν=—1/7 和ν=—1/5 處的復合費米子態表現出明顯的粒子空穴不對稱行為,這也暗示存在較強的朗道能級混合.
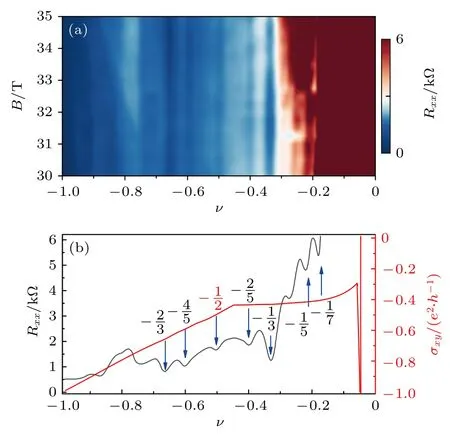
圖3 —1<ν< 0 時的分數量子霍爾態 (a) 溫度T=0.3 K與電位移場D=—0.12 V/nm 時,縱向電阻Rxx 隨填充因子ν 和磁場B 變化的二維圖;(b) 固定溫度T=0.3 K、電位移場D=—0.12 V/nm 與磁場B =31.58 T 時,縱向電阻Rxx (黑色)和橫向電導σxy (紅色)隨填充因子ν 的變化Fig.3.FQH states for —1<ν< 0: (a) Rxx as a function of ν and magnetic field B at T =0.3 K and D =—0.12 V/nm;(b) Rxx (black) and σxy (red) versus ν at B=31.58 T,D =—0.12 V/nm and T =0.3 K.

圖4 —2<ν<—3 時的分數量子霍爾態 (a) 溫度T =0.3 K與電位移場D=—0.12 V/nm 時,縱向電阻Rxx 隨填充因子ν 和磁場B 變化的二維圖;(b) 固定溫度T=0.3 K、電位移場D=—0.12 V/nm 與磁場B =28 T 時,縱向電阻Rxx 和橫向電導σxy 隨ν 的變化Fig.4.FQH states for —2<ν<—3: (a) Rxx as a function of filling factor ν and magnetic field B at T= 0.3 K and D =—0.12 V/nm;(b) Rxx (black) and σxy (red) versus ν at B=28 T,D =—0.12 V/nm and T =0.3 K.
為了更清楚地理解半填充處不可壓縮態的性質,研究了在不同磁場下這些分數量子霍爾態的演化.圖5(a)—(c)分別給出了在—3<ν<—2,—1<ν<0 和1<ν<2 內,不同磁場下縱向電阻Rxx隨填充因子ν的變化.在—3<ν<— 2 區間內,磁場升到27.6 T 時,可以看到在ν=—5/2 處電阻開始出現極小值,表明形成了不可壓縮態,并隨著磁場的增高而變強;當磁場增大到28.8 T 時,縱向電阻Rxx降低的幅度達到最大,意味著此時體態能隙達到最大;而接下來繼續升高磁場,不可壓縮態的能隙開始減小(圖5(a)).同樣,在—1<ν<0 和1<ν<2 區間內,隨著磁場的不斷變大,出現在半填充處的不可壓縮態也呈現出先增強后減弱的趨勢,并分別在34 T 和30 T 達到最強(圖5(b)和圖5(c)).這些結果表明出現在雙層石墨烯第一朗道能級內的偶數分母的分數量子霍爾態對磁場有強烈的依賴性,并且只出現在一段磁場區間中,過高或過低的磁場都會削弱半填充處的不可壓縮態,與之前的理論工作一致[20].當磁場增加時,庫侖能與回旋能量之比增加導致偶數分母的FQHE 更強,而當磁場增加到很大時,朗道能級波函數逐漸被極化到n=0 軌道,更傾向于形成復合費米子液體[19].
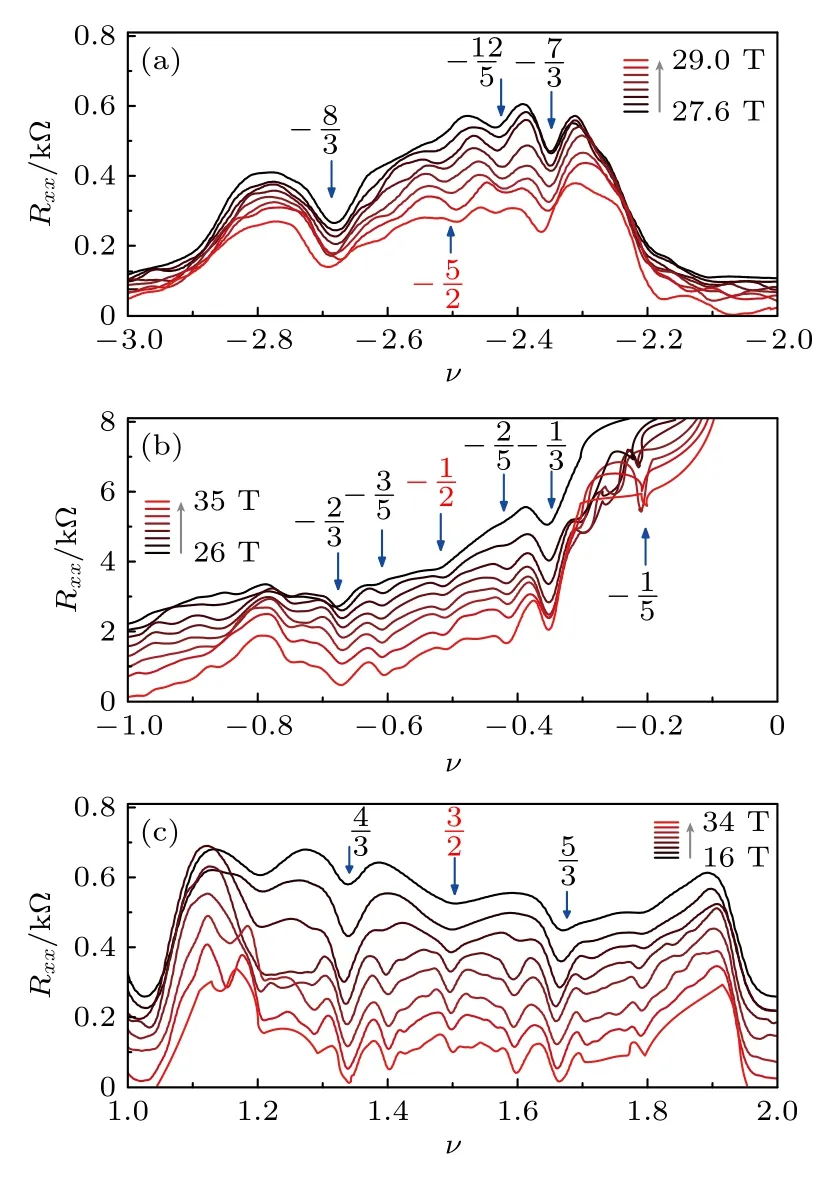
圖5 不同磁場下分數量子霍爾態的演化 (a)—(c) 分別描述了溫度T= 0.3 K 與電位移場D =—0.12 V/nm 時,不同磁場下縱向電阻Rxx 隨填充因子ν 的變化 (為了能在不同磁場下顯示更清楚,每條曲線都加入了偏移量),其中(a) —3<ν<—2,(b)—1< ν<0 和(c) 1<ν<2Fig.5.Evolution of FQH states under different magnetic fields: (a)—(c) Rxx as a function of filling factor ν at T=0.3 K and D=—0.12 V/nm for different magnetic field,corresponding to filling fractions spanning (a) —3<ν<—2,(b)—1<ν<0,and (c) 1<ν<2.
3 結論
綜上所述,我們在雙層石墨烯器件中利用電輸運測量方式觀察到了一系列朗道能級處于半填充的量子霍爾態,對應的填充因子為ν=—5/2,—1/2,3/2.在一定磁場范圍內,半填充的量子霍爾態的強度會隨磁場增加而變強,到達臨界磁場后,量子霍爾態的強度隨磁場的增加逐漸下降.相比于之前的文獻[22]報道,這些量子霍爾態具有更明顯的特征,不僅縱向電阻出現極小值,橫向電導也出現量子化的電導平臺.但是受限于我們的測量手段與器件結構,電中性的邊緣激發模式無法包括在本文數據中,這些不可壓縮態的性質仍然需要進一步的研究來理解.期望未來的研究能夠改進器件結構,利用雙層石墨烯的高度可調控性進行邊緣態隧穿實驗[30]、熱輸運測量[9]、磁學測量[31]、準粒子干涉實驗[32,33]等來直接探測這些基態的低能激發譜與準粒子的統計性質.
感謝中國科學院合肥物質研究院強磁場科學中心提供磁運輸測量儀器,感謝中國科學院強磁場科學中心郗傳英老師和錢英才同學在實驗上對我們的幫助.

