串列彈性雙管渦激振動干涉的仿真研究

王浩杰， 陳正壽， 鮑 健， 杜炳鑫， 屈紹金

(1.浙江海洋大學 船舶與海運學院，浙江 舟山 316022；2.太平洋海洋工程(舟山)有限公司，浙江 舟山 316057)

深海柔性立管因其長徑比大，易產生高階模態的渦激振動(vortex induced vibration，VIV)，容易造成立管的疲勞損傷和破壞。彈性立管尤其是多立管的渦激振動一直是海洋工程領域的研究熱點。受到來流分離以及管間遮蔽效應的影響，多立管的受力與運動極為復雜，容易誘發渦激振動和和尾流誘導振動等強非線性水彈性振動的耦合。

關于管群渦激振動模型試驗研究已有眾多研究成果。Ma等[1-2]研究了3個等間距排列的長彈性圓柱體，著重分析了上游圓柱的尾流對下游圓柱的流體動力系數的影響，并發現當入射角改變時，上、下游彈性圓柱存在不同程度的相互影響。Li等[3]對多管群彈性圓柱體進行模型試驗，結果表明當串列布置時，三管群的斯特勞哈爾數從上游到下游逐漸減小，而五管群均發生渦脫落的增強和抑制。作為管群的一種特殊形式，采用雙管系統更便于研究相鄰管體的振動干涉。大量關于串列雙管的尾流干涉試驗研究發現，下游管體大振幅的尾流誘導振動是由上游管體脫落的漩渦導致的，串列雙管間距中存在充分發展的漩渦決定了下游管體發生尾流誘導振動[4-7]。但是目前普遍存在試驗模型長徑比較小、多測點同時獲取尾流場信息困難等難題。

近些年，CFD(computational fluid dynamics)方法逐漸成為多管體渦激振動分析的主流。Gao等[8]模擬了低雷諾數條件下3個等邊三角形圓柱結構的流動，確定了5種不同的流動狀態，發現尾流的三維特性隨軸間距和雷諾數的增加而增強。Gao等[9]同時對四圓柱結構兩自由度的渦激振動進行分析，發現入射角和約化速度對四圓柱動力響應和尾流形態有顯著的影響。Ribeiro等[10]使用CFX(Computational Fluid X)中的SST(shear stress transfer)湍流模型研究了軸間距和約化速度對二維串列圓柱尾流干涉的影響。Papaioannou等[11]研究了軸間距對二維剛性串列雙圓柱渦激振動的影響，結果表明下游圓柱的最大振幅受軸間距影響較大。Carmo等[12]對串列雙圓柱體的二維、三維流動進行了模擬，觀察到下游圓柱的最大振幅和鎖定范圍明顯高于上游圓柱，三維數值模擬可獲得更準確的柱體受力與結構響應。Chen等[13]基于大渦模擬(large eddy simulation,LES)研究了內、外流對多彈性立管干涉振動的影響，觀察到受下游管振蕩的影響，上游管漩渦脫落頻率增大；當軸間距較小時，下游管的拖曳力系數變的不穩定。Wang等[14]采用雙向流固耦合方法，對串列彈性雙圓柱的渦激振動響應和3種尾渦脫落形式(2S，P+S和2P)進行了研究，得到在小軸間距下，串列彈性圓柱的響應仍以傳統渦激振動為主；隨著軸間距增加，下游圓柱的渦激振動轉變為以尾流誘導振動為主。端木玉等[15]基于自開發深海立管渦激振動求解器，研究了軸間距(1D～4D)對串列雙立管渦激振動的影響，得到不同軸間距上游立管的振動模態均與孤立管相同；受管間干涉作用的影響，下游立管振動模態低于上游立管。武磊等[16]通過對階梯來流中串列雙立管渦激振動的分析，闡明下游立管順流向振動表現出明顯的多模態振動特性。目前就管間振動干涉問題，對小長徑比彈性管和彈性支撐的剛性管涉及較多，對大長徑比串列彈性雙管涉及較少。

本文擬采用雙向流固耦合與時-頻結合的分析方法，開展低雷諾數下，大長徑比串列彈性雙管體渦激振動的干涉研究，系統分析雙管體的振型、結構頻域振動響應、沿管波形與振動模態隨軸間距的變化。其分析結果對實際海洋柔性多管系統渦激振動問題具有一定的參考意義。

1 數值方法

本文采用LES方法對串列彈性雙管體的流場實施模擬，通過求解動力學方程獲取彈性管體的位移變形和振動響應；基于雙向流固耦合方法完成流場和結構場間的數據交換，依靠網格變形技術減少彈性管體變形對流場網格質量的影響。

1.1 流場控制方程

基于有限體積理論，所采用的LES方法通過對不可壓N-S方程進行濾波處理，目的是將一切流動變量劃分為大尺度量和小尺度量，以從流場中去掉小尺度渦，使得大渦運動不受小漩渦影響，導出大渦所滿足方程。可得到濾波后的連續性方程和動量方程

(1)

(2)

1.2 結構動力學方程

基于有限元方法對管體的結構振動進行離散求解，離散后的管體瞬態動力學方程可表示為

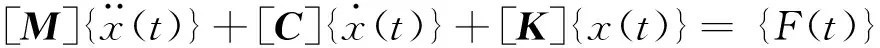
(3)

1.3 雙向流固耦合

在STAR- CCM+中，使用分區算法來解決雙向流固耦合問題，該算法將流體和固體機制分開求解，并通過流固耦合界面將它們連接在一起。換句話說，就是使用流體求解器來獲得流體場，使用固體求解器來求解固體機制，并通過流固耦合方案來連接流體域和固體域的解。在流固耦合交界面上建立位移連續方程和力的平衡方程

ds=df

(4)

τf·nf=τs·ns

(5)

式中：d為位移變量；τ為應力變量；下角標f和s分別為變量為流體和固體一側的變量。

1.4 網格運動模型

在剪切流作用下，大長徑比的彈性管體發生往復性振動，會在管體表面產生較大的位移變形，對結構場和流場網格造成影響。在此，分別采用固體位移運動模型以及變形運動模型來處理耦合交界面變形對于結構場和流場網格的影響。固體位移模型可在結構場求解過程中，自動獲取固體側耦合面節點的位移{x(t)}，并根據{x(t)}完成結構域網格的運動。變形運動模型基于徑向基函數插值方法實現。該方法通過一個方程組生成插值場，使用控制點及其指定的位移創建這些方程，其中每個控制節點的已知位移x′i展開為

(6)

式中：fb,j(rij)為形狀的徑向基本函數；rij為兩個節點之間的距離幅值；λi為展開系數；N為控制節點的數量；α為常數。

2 計算模型

本文以大長徑比串列彈性雙管體為研究對象，開展低雷諾數下的渦激振動干涉研究，相關CFD仿真均基于STAR-CCM+完成。

2.1 大渦模擬(LES)

湍流模型的選擇不僅影響計算準確性，同時還影響計算效率。而湍流模型中的LES方法可以捕捉小尺度渦的信息，真實地反映流場變化產生的湍流，與直接數值模擬相比對計算資源的要求下降很多，與雷諾平均模擬相比流場信息更加豐富。目前采用LES解決了相當數量的流固耦合問題[17-18]。

2.2 計算域及邊界條件

圖1給出了管體系統方形計算域示意圖，為了準確獲取剪切流對于管體渦流場的影響，本文將上游管體安置于距入口邊界下游20D處，并確保尾流域長度為50D，即順流向長度Lx=70D+s，s為雙管間的軸間距。為了減小展向邊界對流場的干擾，計算域橫流向寬度Lz取為40D。

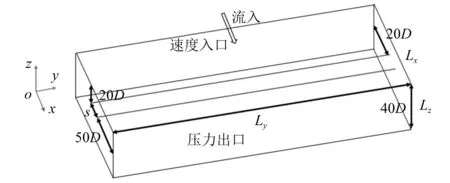
圖1 串列雙管體VIV計算模型示意圖Fig.1 Schematic diagram of the tandem dual pipes VIV calculation model

如圖1所示，流場計算域的左側采用速度入口邊界，右側采用壓力出口邊界，橫流向及管長方向的邊界均設置為對稱邊界，流體和固體管體的交界面設置為流固耦合邊界。對于線性剪切流工況，通過A端固定(實際流速為0)，B端鉸接(流速最大)的方式約束彈性管兩端，并在B端施加管軸向(負y方向)的預張力，數值仿真所建立的管體模型示意圖，如圖2所示。在相應的模型試驗中，參考Chen等[19-20]的相關試驗，采用質輕且堅硬的玻璃纖維增強塑料(fibreglass reinforced plastics,FRP)作為大長徑比彈性管材料，具體參數，如表1所示。

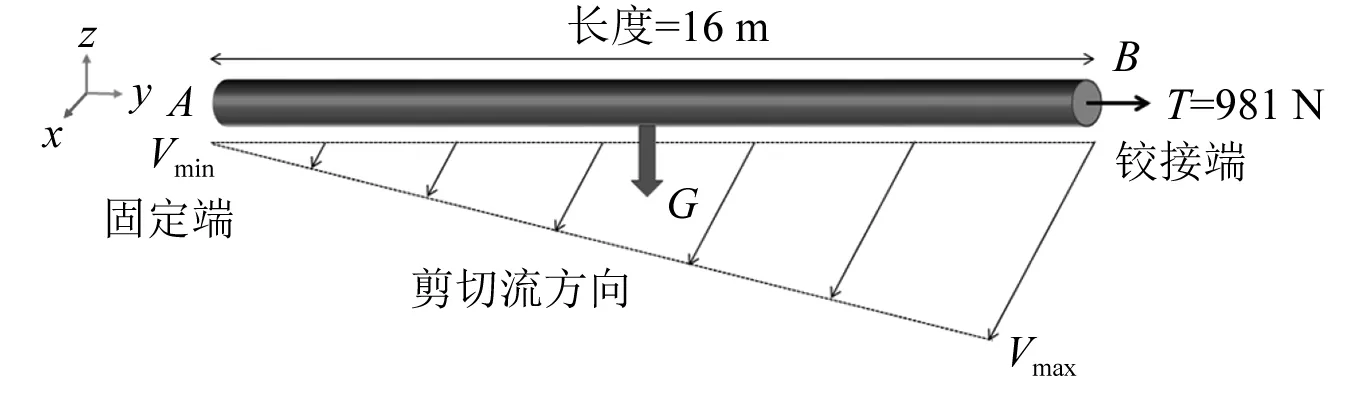
圖2 數值仿真模型剪切流施加示意圖Fig.2 Sketch of shear flow imposed in numerical simulation

表1 細長管道系統參數表Tab.1 Information of the slender pipe system parameters table

2.3 網格劃分

圖3為管體結構部分的網格劃分，由于FRP管硬度相對較高，振動場的局部應變較小，在此采用較大的徑向網格間距對管體進行網格劃分，周向均布節點20個。圖4為管體外流場的網格拓撲結構圖，流場域采用多面體網格進行劃分，為了保證計算精度和減少網格數量，使用棱柱邊界層對近壁面網格進行劃分，并對管體周圍湍流核心區網格進行局部加密。其壁面y+<0.5，滿足LES方法的計算要求。

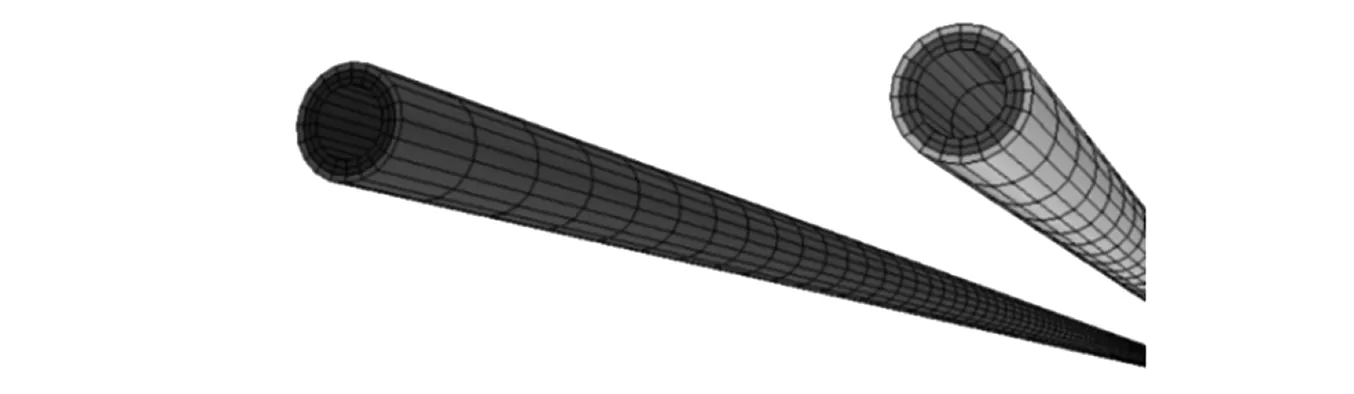
圖3 管道結構的網格劃分Fig.3 Topology of structural domain related to dualpipes

圖4 流體域的網格劃分Fig.4 Topology of fluid domain

2.4 網格依賴性驗證

為了減小計算網格不合理設置對串列雙管體渦激振動研究的不利影響，本文以小長徑比單圓柱體作為測試對象，開展網格依賴性驗證。根據測試結果，選取合適的網格拓撲結構和尺寸，實施大長徑比下單管和不同軸間距下的串列彈性雙管體的渦激振動干涉計算。

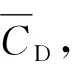
表2 CFD網格依賴性研究結果

基于該網格拓撲結構和網格密度設定，前期已開展關于單彈性管渦激振動與對應模型試驗結果的對比，詳見Chen等和Bao等的研究，經驗證該數值計算結果與模型試驗結果吻合良好。

3 振動響應與分析

針對于第2章所建立的模型，實施剪切流速0.3 m/s，0.5 m/s，軸間距s=3.5D，s=5D和s=6.5D下的串列彈性雙管體雙向流固耦合仿真分析。參考Wang等研究的設定，且考慮到本文采用的是大長徑比下的16 m彈性管體，同時增加s=6.5D軸間距下的工況。在此分別對振動形態、頻譜、沿管體波形與振動模態展開系統化分析。數值仿真模型運算條件設定6個計算工況，如表3所示。

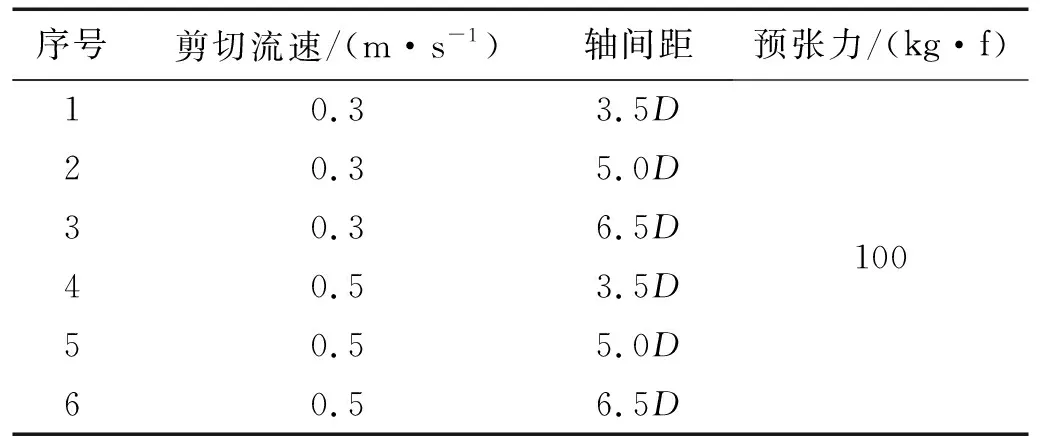
表3 模型條件設定

3.1 振型分析

串列彈性雙管體軸間距的改變可以明顯影響上、下游管體的振型。為更好地對比分析軸間距改變對振動形態的影響，在此將單管與雙管進行比較說明。研究表明，管體在中間部位總體變形較大，在低頻范圍內，振動幅度相對較高[21]。在數值仿真結果的處理中，為開展系統比較，在此選取單管與雙管中部位置(y=8 m)穩定振動階段的響應情況進行分析。

圖5～圖8分別給出了單管以及s=3.5D，s=5.0D和s=6.5D的串列雙管上、下游管體的無因次位移隨時間變化曲線。無因次位移的計算公式為

(7)

“同相”(上、下游管體在同一時刻朝同一方向振動)和“反相”(上、下游管體在同一時刻朝相反方向振動)振動過程在管體的順流向和橫流向上普遍存在。由圖5～圖8可以觀察到上、下游管體的振型呈現出諧振特征。這種雙彈性管渦激振動為典型的“同相”和“反相”振動過程。在順流向上，在s=3.5D算例中，0.8～8.0 s內為“同相”振動過程；在s=5.0D算例中，2.9～11.5 s內為“同相”振動過程；在s=6.5D算例中，0～3.0 s內為“同相”振動過程，6.4～11.2 s內則為“反相”振動過程。在橫流向上，在s=3.5D算例中，4.0～8.2 s和12.5～15.0 s內為“同相”振動過程；在s=5.0D算例中，8.5～9.5 s內為“同相”振動過程，4.5～6.5 s和12.0～15.0 s內則為“反相”振動過程；在s=6.5D算例中，7.3～14.4 s內為“同相”振動過程，0～2.5 s內則為“反相”振動過程。因此順流向的雙彈性管間的這種“諧振”過程是強化這種橫流向的“同相”和“反相”的主導誘因。這種同相作用和反相作用被短時間破壞是由于尾流區的瀉渦重組造成的。如圖9所示，在Vmax=0.3 m/s，s=3.5D的工況下，沿管體跨度2 m，5 m，8 m，11 m，14 m處的尾渦脫落形態出現瀉渦重組的現象。在s=5.0D算例中的橫流向上，“同相”和“反相”振動過程之間存在過渡段；6.5～8.5 s內為“反相”振動向“同相”振動轉換的階段，9.5～12.0 s內為“同相”振動向“反相”振動轉換的階段。這樣的“過渡段”相當于一個模態轉變又重新轉回的過程。

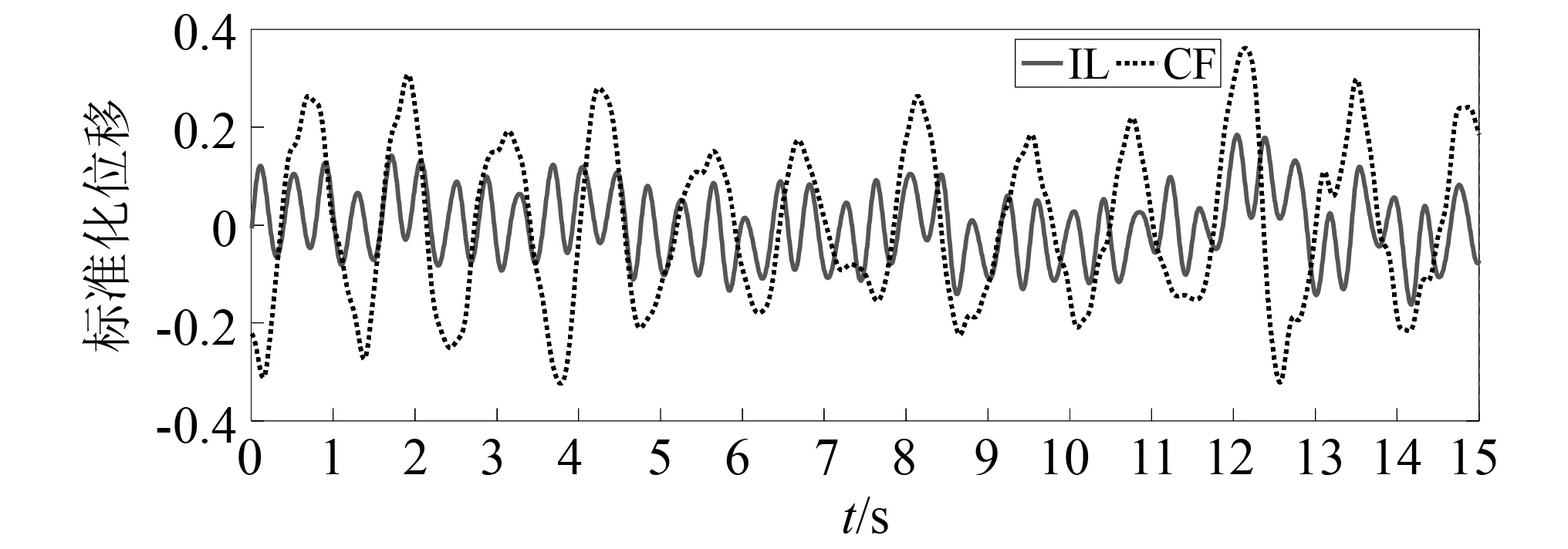
圖5 剪切流速Vmax=0.3 m/s時，單管的振動標準化位移Fig.5 Normalized VIV displacement of a single pipe when Vmax=0.3 m/s

圖6 當間距s=3.5D，剪切流速Vmax=0.3 m/s時，上、下游 管體的振動標準化位移Fig.6 Normalized VIV displacement of upstream and downstream pipes when s=3.5D，Vmax=0.3 m/s

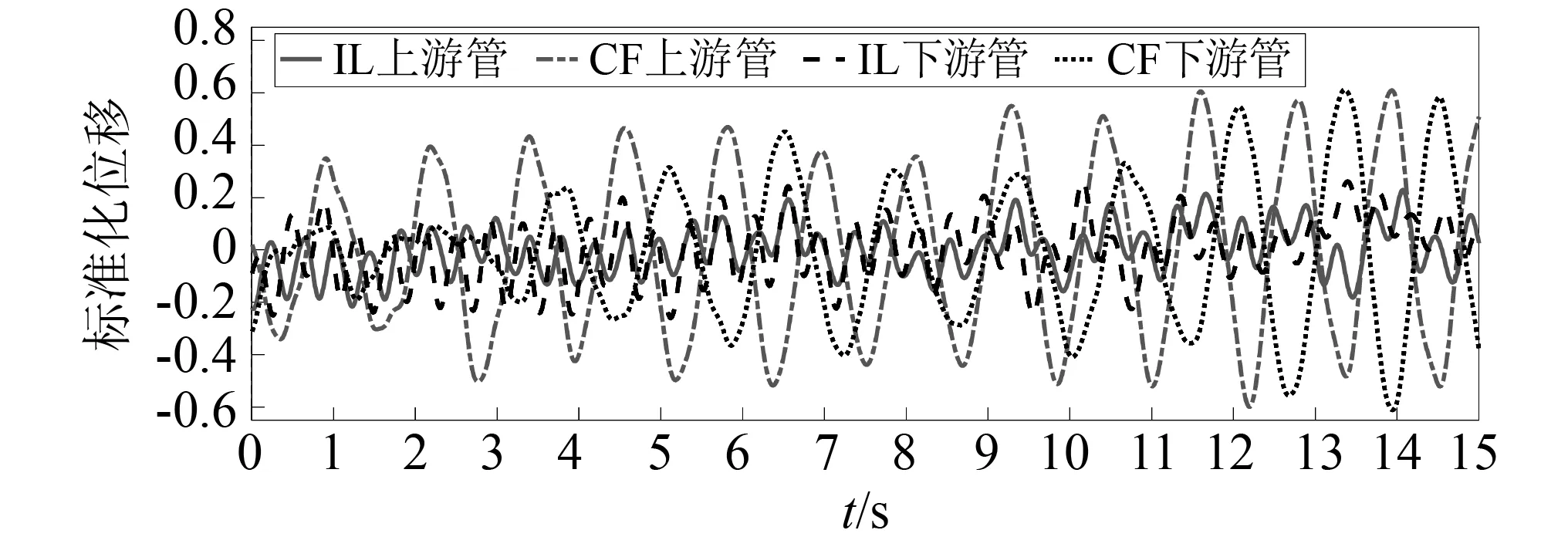
圖7 當間距s=5.0D，剪切流速Vmax=0.3 m/s時，上、下游 管體的振動標準化位移Fig.7 Normalized VIV displacement of upstream and downstream pipes when s=5.0D，Vmax=0.3 m/s

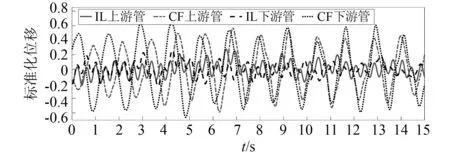
圖8 當間距s=6.5D，剪切流速Vmax=0.3 m/s時，上、下游 管體的振動標準化位移Fig.8 Normalized VIV displacement of upstream and downstream pipes when s=6.5D，Vmax=0.3 m/s

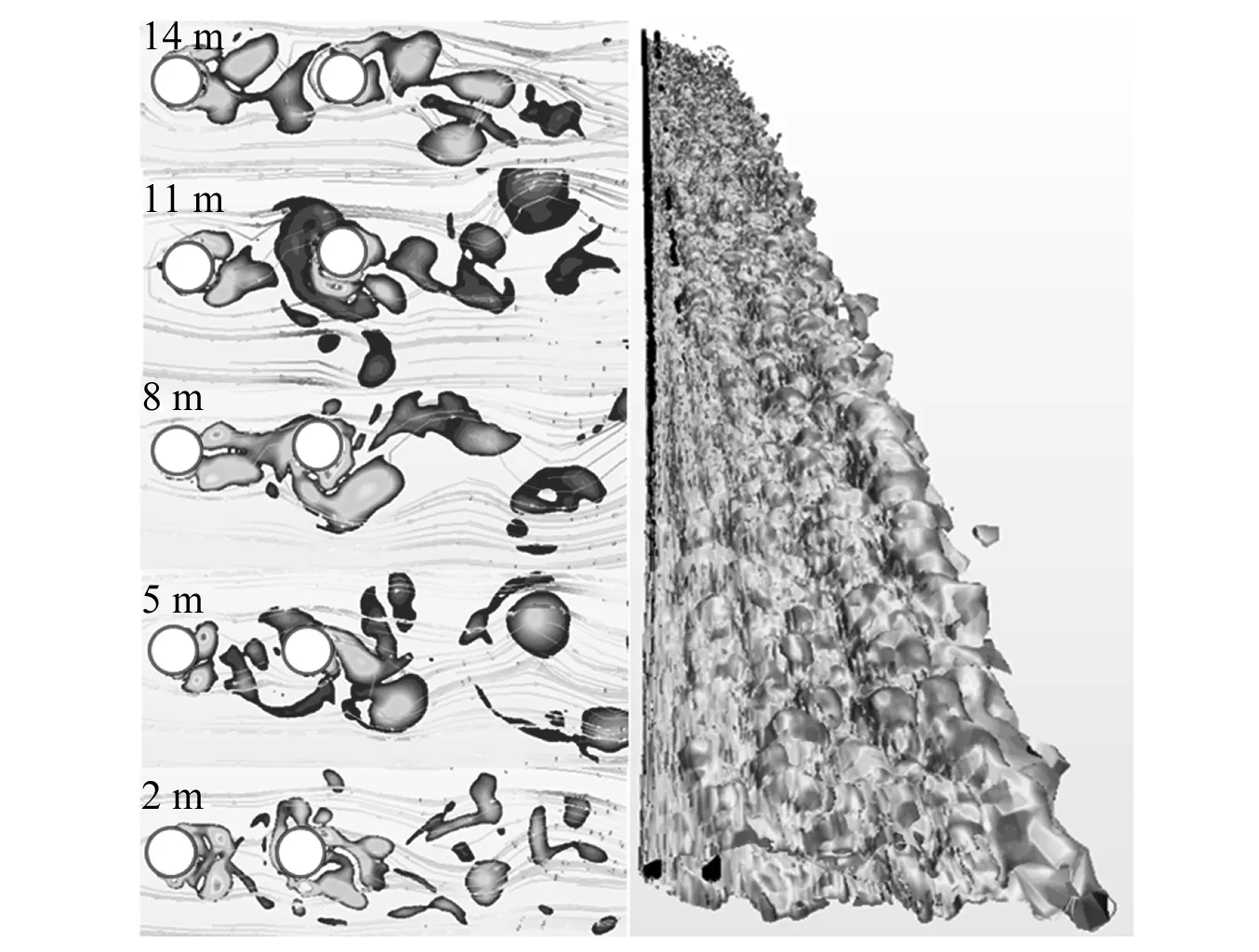
圖9 當間距s=3.5D，剪切流速Vmax=0.3 m/s時，沿管體 跨度的尾渦脫落形態(左)和渦量等值線(右)Fig.9 The wake vortex shedding shape (left) and the vorticity contour (right) along the span of the pipe when s=3.5D， Vmax=0.3 m/s

單管和上、下游管體在順流向和橫流向的振型受軸間距的影響存在一定差異。綜合分析圖5～圖8，從順流向的振型可以看出：不同軸間距下，上游管體的平均振幅與單管差異并不顯著，下游管體的平均振幅稍大于單管，隨軸間距的增大，幅度逐漸減小。相較于單管的振型，除了在s=3.5D的算例中下游管體的振型不太規則，導致此時的平均振動周期小于其他工況，其他軸間距算例中，上、下游管體的振型皆較為規律。由此可知，在順流向上，下游管體受上游管體尾流干涉的影響較為顯著，隨軸間距的增加干涉效應逐漸減弱。而上游管體受兩管間干涉的影響較小，振幅、周期及振型與單管相似。

從橫流向的振型可以看出：不同軸間距上、下游管體的平均振幅明顯大于單管，這主要是由于下游管體在順流向的往復反彈與阻滯作用耦合造成的橫流向的升力增大。其中上游管體的平均振幅受軸間距變化的影響較小，下游管體隨軸間距增大，其平均振幅逐漸接近上游管體，這是由于軸間距的增大，導致下游管體受上游管體尾流干涉的影響逐漸減弱。總體來說，不同軸間距下，上游管體的振型都較為規律，而下游管體的振型在s=3.5D和s=5.0D的算例中較為混亂，在s=6.5D的算例中振型重新變得較為規律。

相較于順流向，下游管體橫流向的平均振幅和振型受上游管體尾流干涉的影響更為顯著。同時，上游管體橫流向的平均振幅受管間相互干涉的影響也較為顯著。另外，在s=3.5D的算例中，下游管體順流向和橫流向的振型受干涉影響尤為突出。

3.2 頻譜分析

為研究串列彈性雙管體的響應頻率，圖10和圖11分別給出了當串列雙管剪切流速為0.3 m/s，s=3.5D,s=5.0D和s=6.5D時，上、下游管體順流向位移和橫流向位移的功率譜密度(power spectral density, PSD)曲線。

圖10 當流速Vmax=0.3 m/s時，不同軸間距下順流向位移的頻譜分析Fig.10 Frequency spectrum analysis of IL VIVwith different axis spacings when Vmax=0.3 m/s for upstream pipe

圖11 當流速Vmax=0.3 m/s時，不同軸間距下橫流向位移的頻譜分析Fig.11 Frequency spectrum analysis of CF VIVwith different axis spacings when Vmax=0.3 m/s for upstream pipe

上、下游管體在順流向普遍存在“多頻共存”現象。由圖10可以看出，其振動表現出明顯的多頻振動特性，或存在多個主導頻率，振動能量較為分散。在保持基本振動能量不變的情況下，主振動頻率會發生跳躍式的變化。如果這種能量轉移不徹底，則會產生明顯的“多頻共存”現象。如圖10(a)所示，y/L=0.5處為明顯的“雙頻共存”現象，y/L=0.25，0.75處為明顯的“三頻共存”現象。在多頻共存的現象中，存在一種特殊的“雙主頻”現象，即次振動頻率所攜帶的能量與主振動頻率所攜帶的能量十分接近，如圖10(a)中管體兩端位置(y/L=0.125，0.875)處所示。

上、下游管體在順流向上的主振模態受軸間距的影響存在差異。圖10(a)～圖6(c)分別為3組軸間距條件下上游管體順流向位移的頻譜分析。不同軸間距下，上游管體不同位置均存在一個主振動頻率，其振動能量最高；一至兩個顯著次振動頻率，其振動能量與主振動頻率具有可比性；若干個伴生振動頻率，其振動能量與主振動頻率所具有的振動能量存在明顯的差異，對主振模態幾乎沒有影響。其中次振動頻率主要是由不規則瀉渦脫落所誘發的隨機振動。在s=3.5D的算例中，上游管體的主振模態明顯為2階。在s=5.0D，s=6.5D的算例中，由于上游管體部分位置主振動頻率的振動能量減小，多處位置存在“三頻共存”現象，其中兩個顯著次振動頻率的振動能量相近，故主振模態增大到3階。

圖10(d)～圖10(f)分別為3組軸間距值s=3.5D，s=5.0D和s=6.5D條件下下游管體順流向位移的頻譜分析。不同軸間距下，下游管體不同位置均存在一個主振動頻率，1～3個顯著次振動頻率和若干個伴生振動頻率。在s=3.5D的算例中，下游管體多個位置存在一個主振動頻率和一個次顯著振動頻率，且兩者的振動能量相近，故主振模態為2階；在s=5.0D的算例中，下游管體多處位置存在“三頻共存”現象，在s=6.5D的算例中，下游管體多處位置存在“雙主頻”現象。由于軸間距增大到5.0D和6.5D時，兩者頻率的振動能量相差略小，故主振模態以3階或4階為主。

由此可知，軸間距的增加對上游管體的主振模態影響略小，對下游管體的主振模態影響較為顯著。這是由于下游管體受上游管體尾流的影響，下游管體在順流向的振動更容易表現出多頻振動特性。

在相同軸間距下，上、下游管體頻率的振動能量存在一定差異。對比分析圖10(a)和圖10(d)可以看出，在s=3.5D的算例中，上游管體各位置主振動頻率的振動能量PSD值普遍高于0.08，在y/L=0.25處PSD值高達0.11，而下游管體的PSD值普遍在0.06上下浮動，可以看出此間距算例對應的上游管體各位置主振動頻率的振動能量明顯高于下游管體。同時上游管體的多個顯著次振動頻率的振動能量略低于下游管體。由此說明此間距算例對應的上、下游管體受管間干涉影響顯著。如圖10(b)、圖10(e)和圖10(c)、圖10(f)所示，在s=5.0D，s=6.5D的算例中，由于軸間距增加導致上、下游管體管間的干涉影響逐漸減弱，管體不同位置振動頻率的振動能量差異并不顯著。

上、下游管體在橫流向上的振動能量出現規律性變化。由圖11可以看出，低頻對應于較大的功率譜密度，其主要原因是低頻振動時，管體橫流向位移的平均值較大，能量較高。上、下游管體不同位置均存在一個主振動頻率和若干個伴生振動頻率，其中各位置的主振動頻率均在0.9 Hz左右。當主振動頻率的振動能量增大/減小時，伴生振動頻率的振動能量相應出現減小/增大的變化。同時，隨軸間距增大，上、下游管體兩端位置主振動頻率的振動能量皆呈現出先增大后減小的趨勢，而管體中間位置主振動頻率的振動能量呈現相反趨勢。其中在s=5.0D的算例中，管體兩端以駐波振動模式為主，振動能量高，管體中部以行波振動模式為主，振動能量低。

上、下游管體在順流向和橫流向上的運動響應存在一定差異。如圖10和圖11所示，管體在順流向上存在1～3個主導響應頻率和若干個次響應頻率，而橫流向上只存在一個主導響應頻率和若干個次響應頻率。這是橫流向運動和順流向運動間相互作用引起彈性管體的高次諧波位移響應。同時可以觀察到上、下游管體在不同軸間距下的算例中，橫流向的主振動頻率約為0.9 Hz，順流向的主振動頻率約為1.9 Hz和3.2 Hz，當順流向出現“三頻共存”現象時，4.4 Hz的次響應頻率躍升為主導響應頻率。

3.3 沿管體波形與振動模態分析

伴隨著管體振型發生改變，管體振動能量也隨之改變。在此通過對比管體的時間-位置云圖分析軸間距和速度對串列彈性雙管體沿管波形和振動模態的影響，從而進一步說明管體在順流向振動的多模態特性。圖12～圖17給出了剪切流速為0.3 m/s，3種軸間距下的上、下游管體順流向時間—位置云圖。圖中x軸為時間t，分別截取t=10～20 s或t=30～40 s的結果進行分析，y軸為管體位置。

上、下游管體的順流向振動均表現出明顯的多模態振動特性。如圖12和圖13所示，在s=3.5D的算例中，上、下游管體的主振模態均為2階，且伴隨有較弱的3階模態。圖12中可以觀測到明顯的模態轉換現象，在t=33～36 s內，上游管體的振動模態由2階轉換為3階，在t=36～40 s內，其振動模態又由3階轉換為2階。如圖14所示，在s=5.0D的算例中，上游管體存在顯著的3階模態和較弱的2階模態，由于振動能量發生耗散，管體短暫地出現了較弱的4階模態，故主振模態為3階。從圖15可以看出，下游管體的主振模態為3階，但2階模態的也相對較顯著，并未發現4階模態。如圖16和圖17所示，在s=6.5D的算例中，上游管體的主振模態為3階，且伴隨有較弱的2階模態；下游管體的主振模態變為4階，結合上文對此間距下的頻譜分析發現，該間距下伴隨有較弱的3階模態。

圖12 當間距s=3.5D，剪切流速 Vmax=0.3 m/s時，上游管體順流向 時間-位置云圖Fig.12 IL time-position contour of the upstream pipe in the case of s=3.5D, when Vmax=0.3 m/s

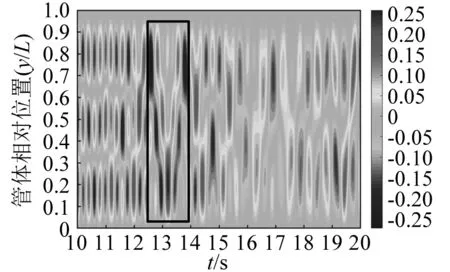
圖13 當間距s=3.5D，剪切流速 Vmax=0.3 m/s時，下游管體順流向 時間-位置云圖Fig.13 IL time-position contour of the downstream pipe when s=3.5D， Vmax=0.3 m/s

圖14 當軸間距s=5.0D，剪切流速 Vmax=0.3 m/s時，上游管體順流向 時間-位置云圖Fig.14 IL time-position contour of the upstream pipe when s=5.0D， Vmax=0.3 m/s

圖15 當間距s=5.0D，剪切流速 Vmax=0.3 m/s時，下游管體順流向 時間-位置云圖Fig.15 IL time-position contour of the downstream pipe when s=5.0D， Vmax=0.3 m/s

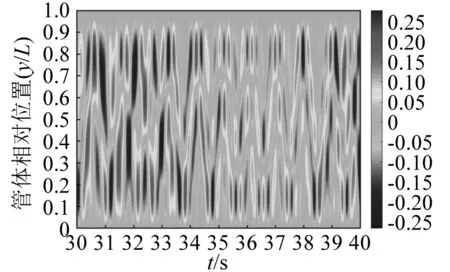
圖16 當間距s=6.5D，剪切流速 Vmax=0.3 m/s時，上游管體順流向 時間-位置云圖Fig.16 IL time-position contour of the upstream pipe when s=6.5D， Vmax=0.3 m/s

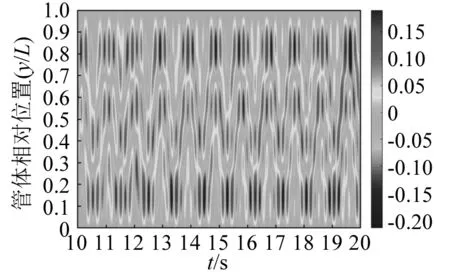
圖17 當間距s=6.5D，剪切流速 Vmax=0.3 m/s時，下游管體順流向 時間-位置云圖Fig.17 IL time-position contour of the downstream pipe when s=6.5D， Vmax=0.3 m/s

由此可知，在同一剪切流速Vmax=0.3 m/s的工況下，由于雙管間的相互干涉，下游管體受軸間距的影響更為顯著，s從3.5D，5.0D增加到6.5D時，上游管體的主振模態從2階增加到3階，而下游管體的主振模態依次從2階、3階增加到4階。

剪切外流作用下，細長彈性管體兩端主要以駐波振動模式為主，中部主要為駐波振動模式和短式行波振動模式交替出現。綜合分析圖12～圖17，隨軸間距增大，行波持續現象和間斷性出現的短式行波頻率變高。在圖13中，出現了明顯的駐波振動模式和行波振動模式相互轉換的現象。在t=10～13 s內，下游管體的振動模式由駐波振動模式轉換為行波振動模式，在t=13～16 s內，其振動模式又由行波振動模式轉換為駐波振動模式。且在行波振動模式下，存在波形的振動反射。圖14中，在t=36.3～37.4 s內行波經反射回彈形成一個振動周期，這是由于管體長度及振動產生半個相位造成的。同類現象也出現在圖15中的t=30.7～31.7 s時間段內。

在Vmax=0.5 m/s的工況下，多模態振動特性仍普遍存在。上、下游管體的主振模態均為4階，存在3階振動模態與4階振動模態相互轉換的現象。隨軸間距增大，3階模態的比重逐漸減少，而4階模態的比重逐漸增加，出現較弱的2階和5階振動模態。這是因為下游管體受上游管體尾流干涉的影響，隨軸間距增大，尾流干涉影響逐漸減弱，因此3階模態的比重減少，相比之下4階模態的比重逐漸增加，符合端木玉等的結論。多模態振動特性可以解釋為，上游管體的尾流對下游管體的瀉渦影響很大，使得下游管體的瀉渦頻率不穩定，進而造成了下游管體順流向的多模態振動。同時，處于上游管體尾流中的下游管體對流場的反射及對上游管體泄渦的影響使得上游管體主振模態以及主振模態的比重增加，進而造成上游管體順流向的多模態振動。

圖18和圖19代表性地給出了上、下游管體的順流向時間-位置云圖，其中s=5.0D，剪切流速為0.5 m/s。與同間距比下的圖14和圖15相比，流速的增大使得上、下游管體順流向主振模態從3階增加到了4階，同樣呈現出多模態振動特性。如圖18所示，在t=30.0～31.5 s內發現了較弱的5階振動模態。另外，流速的增大使得沿管波形變得混亂，駐波振動模式減少，相應的行波振動模式頻率變高。圖18的t=33.8～39.8 s和圖19的t=10.2～10.8 s時間段內均可觀察到行波振動模式。

圖18 當間距s=5.0D，剪切流速Vmax=0.5 m/s時， 上游管體順流向時間-位置云圖Fig.18 IL time-position contour of the upstream pipe when s=5.0D，Vmax=0.5 m/s

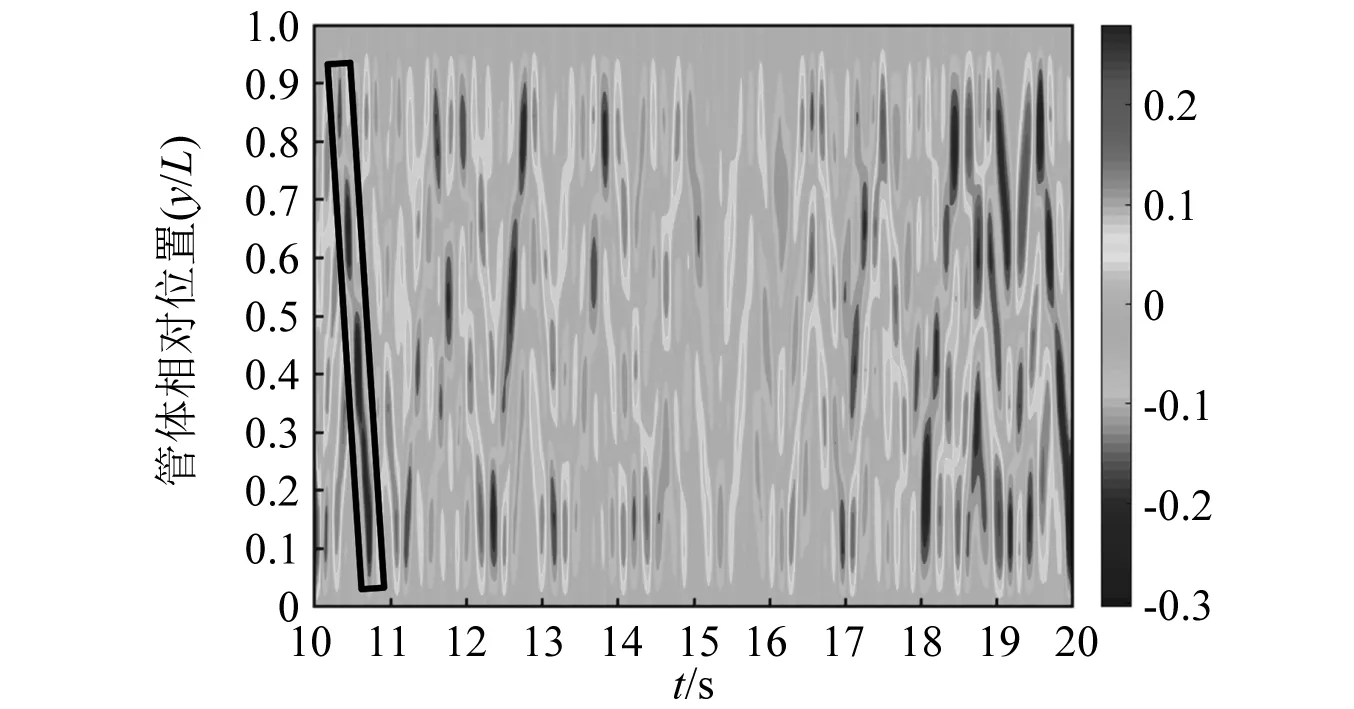
圖19 當間距s=5.0D，剪切流速Vmax=0.5 m/s時， 下游管體順流向時間-位置云圖Fig.19 IL time-position contour of the downstream pipe when s=5.0D，Vmax=0.5 m/s

4 結 論

本文基于CFD技術開展了低雷諾數條件下串列彈性雙管體渦激振動干涉的仿真研究。采用多種剪切流速和軸間距來研究對串列雙管體渦激振動的影響，通過對幾種工況中上、下游管體的振型、頻率響應以及沿管波形與振動模態進行分析，得出以下結論。

(1)在中間部位處，上游管體的振型與單管差異并不顯著，而下游管體的振型受軸間距影響顯著。且單管與上、下游管體均出現“同相”和“反相”振動。

(2)上、下游管體在順流向和橫流向上均呈現出多頻振動特性，且在順流向上出現了“雙主頻”現象。隨軸間距增大，其各位置主振動頻率的能量在順流向和橫流向上呈現出不同的增減趨勢。

(3)不同軸間距下，上、下游管體在順流向上均呈現出多模態振動特性和模態間相互轉換的現象，可以觀察到駐波振動模式和行波振動模式下的反射現象。下游管體振動模態受軸間距的影響更為顯著。