考慮石膏質(zhì)巖膨脹性的圍巖分級修正

楊 陽

(中鐵十一局集團(tuán)有限公司 湖北武漢 430063)

1 引言

隨著我國隧道工程建設(shè)加快，不可避免會遇到含石膏質(zhì)巖地層。作為一種蒸發(fā)沉積巖，石膏和硬石膏在地層中分布廣泛。石膏質(zhì)巖中硬石膏遇水生成石膏(AGT)，導(dǎo)致體積增大，使得石膏質(zhì)巖表現(xiàn)出膨脹性。從巖石膨脹機(jī)理角度可將膨脹巖分為兩類:一種是像硬石膏、芒硝一樣通過化學(xué)反應(yīng)將自由水變成結(jié)合水，另一種是所含黏土礦物吸水后晶層間距變大。

針對石膏質(zhì)巖膨脹性這一問題，劉艷敏等[1]通過試驗分析了不規(guī)則發(fā)育的硬石膏巖重塑樣吸水膨脹壓力大小與初始含水率的關(guān)系，初始含水率越高，重塑樣吸水率越低；膨脹壓力與初始含水率成反比，并近似呈線性關(guān)系。Alonso等[2]對Lilla隧道現(xiàn)場進(jìn)行觀察發(fā)現(xiàn)石膏質(zhì)巖膨脹是由于石膏晶體不連續(xù)生長所導(dǎo)致。Wanninger[3]對Belchen隧道的硬石膏巖試樣進(jìn)行側(cè)限膨脹試驗，發(fā)現(xiàn)常溫條件下，硬石膏巖的膨脹不只有AGT引發(fā)的膨脹，還有黏土礦物吸水引起的膨脹。任松等[4]對硬石膏圍巖在壓力水作用下的軸向膨脹應(yīng)變及側(cè)向膨脹應(yīng)力進(jìn)行測試，建立了壓力水作用下的硬石膏巖吸水狀態(tài)方程，并改進(jìn)了濕度場理論體系中的膨脹本構(gòu)模型。

對于石膏質(zhì)巖膨脹性的研究，目前的方法沒有考慮到石膏質(zhì)巖膨脹性的特性。本文考慮膨脹壓力的影響，對?鐵路隧道設(shè)計規(guī)范?中圍巖壓力與圍巖級別的統(tǒng)計關(guān)系式進(jìn)行修正，建立膨脹壓力與圍巖級別的關(guān)系。基于考慮膨脹壓力的修正圍巖級別與圍巖分級BQ關(guān)系，引入考慮膨脹性影響的修正系數(shù)，建立考慮石膏質(zhì)巖膨脹性的圍巖分級修正方法。通過實(shí)際工程案例進(jìn)行驗證，論證了該方法的實(shí)用性。

2 石膏質(zhì)巖膨脹機(jī)理和危害

石膏質(zhì)巖膨脹主要包括兩個過程，一是石膏質(zhì)巖的孔隙吸水，巖石顆粒骨架中產(chǎn)生負(fù)有效應(yīng)力使體積發(fā)生膨脹，并與吸水同步發(fā)生，顆粒之間的水膜厚度增大，使體積增大；二是吸水之后，硬石膏顆粒和水發(fā)生化學(xué)反應(yīng)導(dǎo)致體積膨脹。結(jié)合石膏質(zhì)巖的膨脹機(jī)理，其危害總結(jié)如下:

(1)石膏質(zhì)巖中含有的硬石膏水化膨脹產(chǎn)生的膨脹壓力導(dǎo)致巖體產(chǎn)生空隙和裂縫，使得應(yīng)力場發(fā)生變化[5]，并為地下水滲流提供了路徑。

(2)空隙和裂縫由于巖體膨脹進(jìn)一步發(fā)育再次促進(jìn)了水化反應(yīng)，使圍巖多項物理指標(biāo)下降，自承能力下降，圍巖級別降低。

(3)水化反應(yīng)和膨脹效應(yīng)的相互促進(jìn)，使得圍巖給予襯砌結(jié)構(gòu)的膨脹壓力長期存在，因此病害發(fā)生風(fēng)險較高(見圖1)。

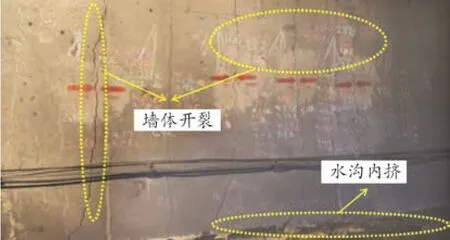
圖1 某隧道由于石膏質(zhì)巖膨脹所引起的病害

3 膨脹壓力簡化計算模型及解析解

3.1 簡化計算模型

目前關(guān)于地下洞室膨脹壓力的研究大都集中在流變效應(yīng)，其次為使用濕度場[6－7]模擬膨脹巖的水化膨脹。這些研究所推導(dǎo)的微分方程系統(tǒng)和本構(gòu)關(guān)系較為復(fù)雜，較難應(yīng)用于實(shí)際工程。本節(jié)基于彈性力學(xué)軸對稱問題[8]，對地下洞室進(jìn)行模型簡化處理，推導(dǎo)膨脹壓力的解析解。

石膏質(zhì)巖地下洞室膨脹壓力的簡化計算模型如圖2所示。圖中:r1為襯砌結(jié)構(gòu)內(nèi)徑；r2為襯砌結(jié)構(gòu)外徑；r3為發(fā)生膨脹的圍巖外徑；r4為未發(fā)生膨脹的巖層外徑；p1和p2分別為圍巖內(nèi)外側(cè)的膨脹壓力。發(fā)生膨脹和未發(fā)生膨脹的巖層膨脹率分別為α1、α2(α1<α2)，其余參數(shù)列于表1 中。

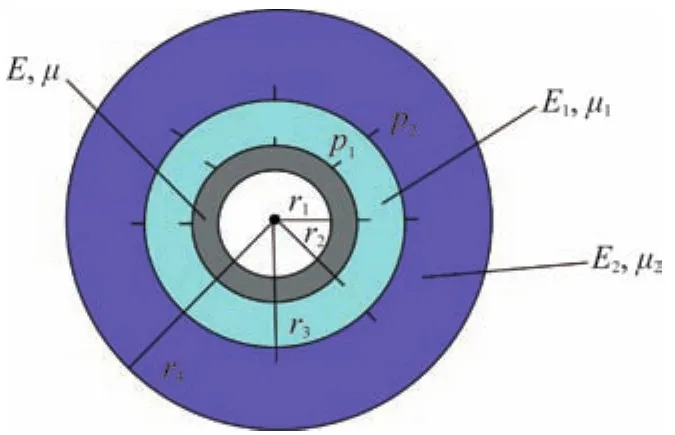
圖2 膨脹壓力簡化計算模型

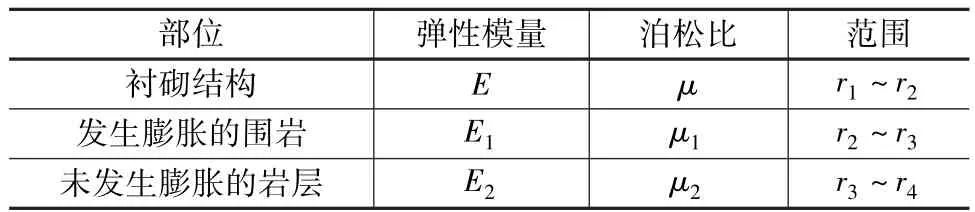
表1 圍巖和襯砌結(jié)構(gòu)參數(shù)

3.2 膨脹壓力解析解推導(dǎo)

參考彈性力學(xué)軸對稱問題中壓力隧洞問題求解[8]和相關(guān)學(xué)者研究成果[9－10]，對推導(dǎo)過程做出如下假設(shè):

圍巖和襯砌結(jié)構(gòu)為各向同性的彈性連續(xù)介質(zhì)；將圍巖所有的膨脹看作線性膨脹。

利用彈性力學(xué)軸對稱問題中的應(yīng)力軸對稱公式和位移軸對稱公式，結(jié)合邊界條件，計算作用于襯砌部分的膨脹壓力的解。彈性力學(xué)軸對稱問題中的應(yīng)力軸對稱公式和位移軸對稱公式如下:

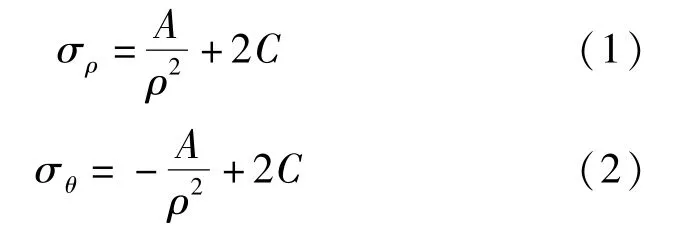
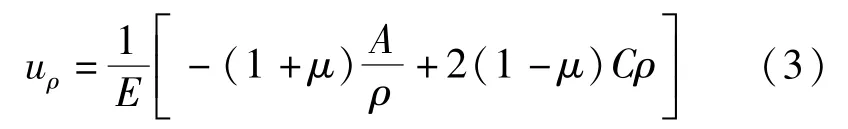
式中:σρ為徑向應(yīng)力；σθ為切向應(yīng)力；μρ為徑向位移；ρ為半徑；A、C為待定常數(shù)項；E、μ分別為彈性模量、泊松比。將上述公式與邊界條件結(jié)合進(jìn)行求解。

(1)對襯砌結(jié)構(gòu)部分進(jìn)行求解

在僅考慮膨脹壓力的前提下，由襯砌結(jié)構(gòu)計算模型得到的邊界條件:

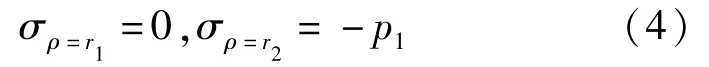
將式(4)代入式(1)，求出A、C兩個待定常數(shù):

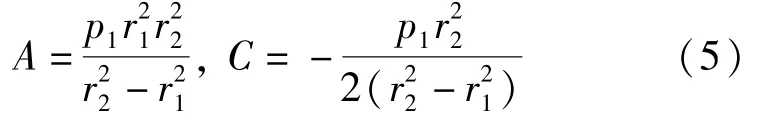
將A、C代入式(1)～式(3)中，可得到襯砌結(jié)構(gòu)部分的應(yīng)力解和位移解:

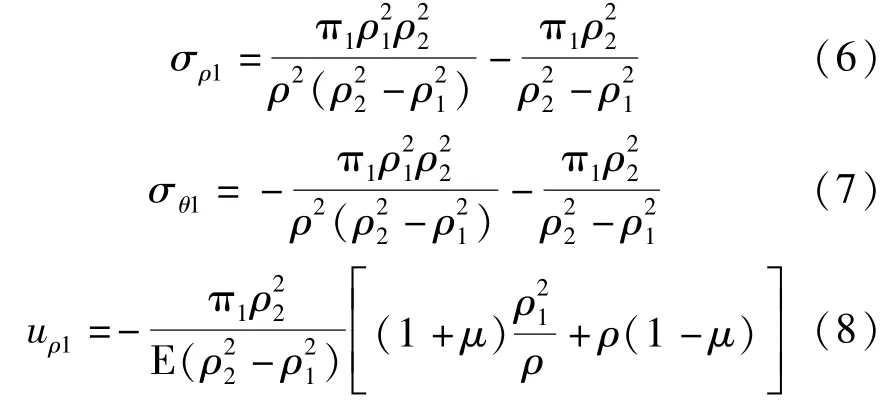
(2)對其他圍巖部分進(jìn)行求解

發(fā)生膨脹的圍巖邊界條件:

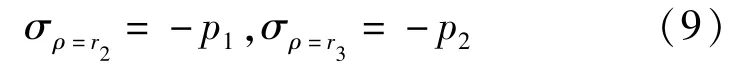
同理可得到發(fā)生膨脹圍巖部分的應(yīng)力解和位移解:

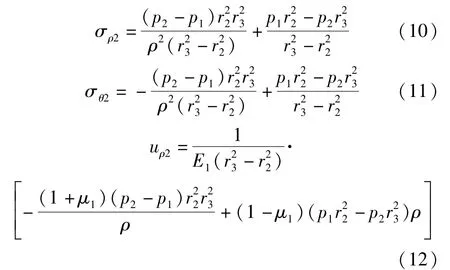
未發(fā)生膨脹的圍巖邊界條件:

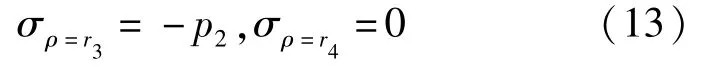
同理可得未發(fā)生膨脹的圍巖部分應(yīng)力解和位移解:

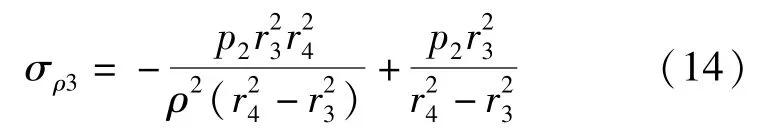
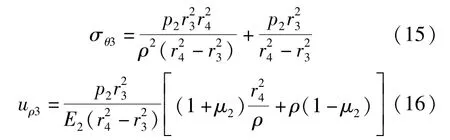
將所得到的三個部分的應(yīng)力解和位移解結(jié)合邊界條件式(17)，便可得出膨脹壓力p1、p2的解。

根據(jù)解析解進(jìn)行計算時，按平面應(yīng)力問題求解，E、E1和μ、μ1按原值代入。由上述推導(dǎo)過程得到的p1，p2的計算公式即為膨脹壓力的解析解。

4 考慮膨脹壓力的圍巖級別修正

4.1 考慮石膏質(zhì)巖膨脹性影響的圍巖壓力

圍巖壓力根據(jù)形式的不同可分為四種:松動壓力、形變壓力、膨脹壓力、沖擊壓力。簡化計算模型未考慮支護(hù)結(jié)構(gòu)和圍巖之間的形變壓力，所以在研究石膏質(zhì)巖地下洞室圍巖壓力時不考慮形變壓力[11]和沖擊壓力。因此，石膏質(zhì)巖地下洞室的圍巖壓力，主要包括松動壓力和膨脹壓力。

4.2 膨脹壓力與圍巖級別關(guān)系的建立

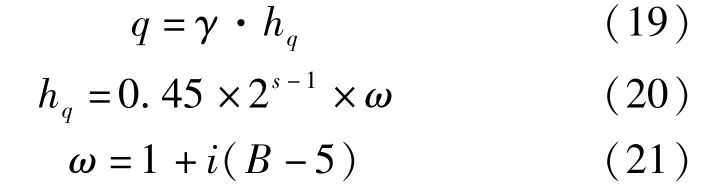
式(19)～式(21)為?鐵路隧道設(shè)計規(guī)范?[11]中關(guān)于深埋鐵路隧道圍巖壓力與圍巖級別的統(tǒng)計關(guān)系式。

式中:q為垂直均布壓力；γ為圍巖重度，kN/m3；hq為等效荷載高度；s為圍巖級別；ω為寬度影響系數(shù)；B為坑道寬度，m；i為B每增加或減少1 m時，圍巖壓力變化速率。

為建立膨脹壓力與圍巖級別的關(guān)系，基于式(19)，引入膨脹壓力指標(biāo)對統(tǒng)計關(guān)系式進(jìn)行修正，可通過修正后的關(guān)系式計算得到考慮膨脹壓力影響的修正圍巖級別。推導(dǎo)過程如下:

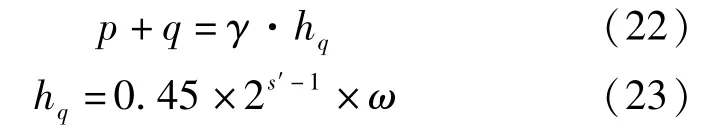
式中:p為膨脹壓力；s′為考慮膨脹壓力影響的修正圍巖級別。將式(19)～式(23)整理如下:

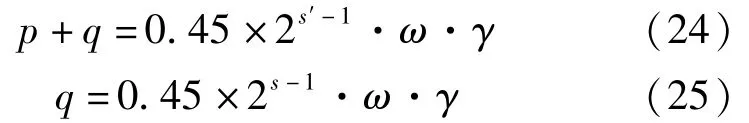
兩式相除得:

將式(19)～式(21)與式(26)聯(lián)立消去參數(shù)，得到膨脹壓力和圍巖級別的關(guān)系式。

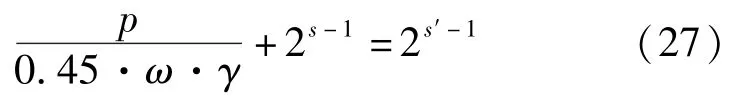
4.3 膨脹壓力對圍巖級別修正的計算說明

在計算膨脹壓力前，需對部分參數(shù)指標(biāo)進(jìn)行取值。

(1)根據(jù)對某石膏質(zhì)巖隧道巖樣的室內(nèi)試驗，膨脹壓力解析解中參數(shù)E1取10 MPa、μ1取0.35；發(fā)生膨脹的巖層彈性模量取3 GPa、μ2取0.35，膨脹率為0%。

(2)襯砌結(jié)構(gòu)彈性模量為33 GPa，泊松比為0.2，厚度為70 cm。

(3)含有石膏質(zhì)巖的巖體巖性較差，絕大多數(shù)圍巖級別為Ⅳ級或者Ⅴ級，所以只考慮膨脹性對圍巖級別為Ⅳ級和Ⅴ級的影響。

(4)為考慮洞室跨度的影響，根據(jù)?鐵路隧道設(shè)計規(guī)范?(TB 10003—2016)，選取 8、10、12、14、16和18 m六種跨度進(jìn)行計算。

(5)通過密度測定后發(fā)現(xiàn)，密度基本分布在2.25～2.4 g/cm3之間，為便于計算，式(25)中參數(shù)γ取2.3 g/cm3。

(6)巖層范圍選取0.25倍、0.5倍和1倍洞室外半徑。

5 膨脹壓力對圍巖級別修正計算和規(guī)律分析

根據(jù)式(27)和計算說明，計算在Ⅳ、Ⅴ級圍巖條件下考慮跨度因素影響的膨脹壓力[12]，再求解膨脹壓力所對應(yīng)的修正圍巖級別。將膨脹壓力的解析解與修正關(guān)系式(27)相結(jié)合，得到式(28)。

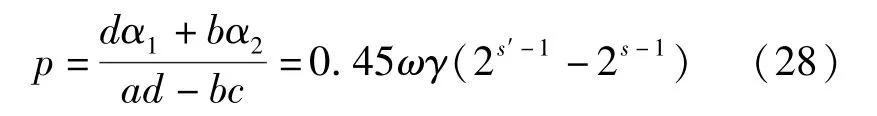
按平面應(yīng)變問題對上述六種跨度，根據(jù)式(19)～式(21)計算對應(yīng)的寬度影響系數(shù)，見表2。

表2 不同跨度所對應(yīng)的寬度影響系數(shù)

將Ⅳ、Ⅴ級圍巖在不同跨度條件下膨脹壓力與修正圍巖級別的函數(shù)關(guān)系式列于表3。

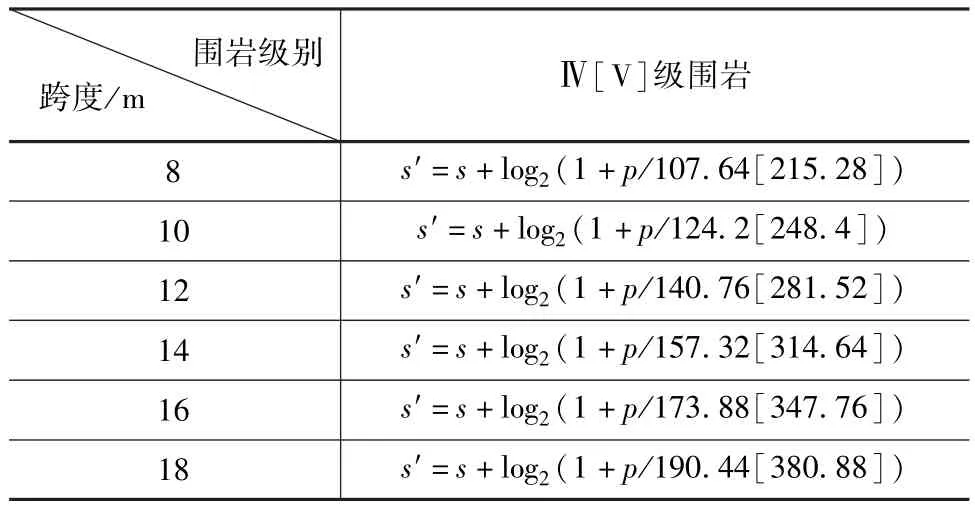
表3 圍巖在不同跨度條件下膨脹壓力與修正圍巖級別的函數(shù)關(guān)系式(中括號內(nèi)為Ⅴ級圍巖關(guān)系式)

為分析計算結(jié)果，定義膨脹比例系數(shù)η＝p/q。將其與式(25)結(jié)合得到膨脹比例系數(shù)的計算公式:

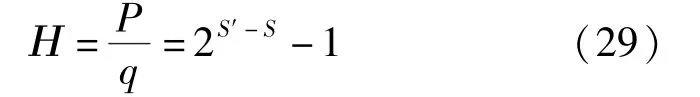
以發(fā)生膨脹的圍巖和未發(fā)生膨脹的巖層范圍選取0.25、0.5、1.0倍洞室外半徑的情況進(jìn)行計算，并繪出Ⅳ、Ⅴ級圍巖洞室跨度對修正圍巖級別以及膨脹比例系數(shù)的影響曲線，見圖3、圖4。

圖3 洞室跨度對修正圍巖級別的影響

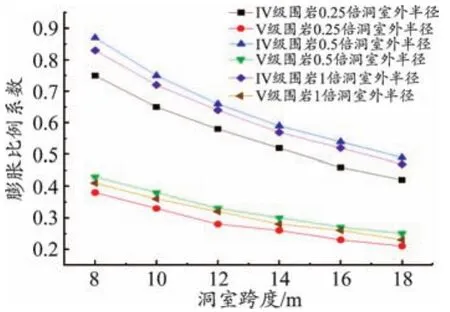
圖4 膨脹比例系數(shù)變化曲線

(1)洞室跨度增大，修正圍巖級別下降，膨脹比例系數(shù)減小。

(2)膨脹壓力受到洞室跨度的影響小，但受發(fā)生膨脹的巖層范圍影響大，原因是石膏質(zhì)巖在巖層中的含量及比例發(fā)生變化，導(dǎo)致膨脹壓力發(fā)生變化。

(3)膨脹比例系數(shù)Ⅴ級圍巖小于Ⅳ級圍巖，且變化曲線相對于Ⅳ級圍巖更為平緩，說明膨脹壓力對于Ⅳ級圍巖的影響更大。

6 考慮膨脹性的石膏質(zhì)圍巖分級修正

圍巖分級BQ給出了不同圍巖級別對應(yīng)的BQ取值范圍，為使修正圍巖級別得以應(yīng)用，可將修正圍巖級別轉(zhuǎn)化為圍巖分級BQ，再通過圍巖分級BQ重新判定圍巖級別。圍巖分級BQ的分級取值范圍如表4所示，并繪制不同圍巖級別和BQ取值范圍的柱狀關(guān)系圖，見圖5。

表4 圍巖分級BQ的分級取值范圍

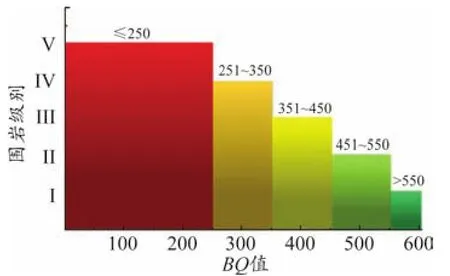
圖5 圍巖級別與BQ的柱狀關(guān)系圖

參考表4與圖5，在Ⅰ、Ⅱ、Ⅲ、Ⅳ、Ⅴ級圍巖的分級取值范圍內(nèi)分別取500、1 000、2 000、4 000和8 000個數(shù)據(jù)點(diǎn)進(jìn)行擬合，擬合結(jié)果如表5所示。

表5 BQ與圍巖級別的擬合函數(shù)

定義膨脹修正系數(shù)BQ，其中BQ′是考慮膨脹壓力影響的修正圍巖級別所對應(yīng)的BQ。

基于擬合結(jié)果計算修正圍巖級別所對應(yīng)的膨脹修正系數(shù)，其范圍為:

Ⅳ級圍巖λP的取值范圍為0.70～0.83，Ⅴ級圍巖λP的取值范圍為0.74～0.86。

將λP與圍巖分級BQ的計算公式相結(jié)合，得到考慮石膏質(zhì)巖膨脹性的圍巖分級修正公式:

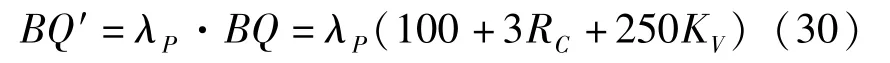
式中:λP為膨脹修正系數(shù)；RC為單軸飽和抗壓強(qiáng)度；KV為完整性系數(shù)。

7 工程案例

為對考慮石膏質(zhì)巖綜合特性的圍巖分級修正方法進(jìn)行驗證，選取某隧道作為依托工程，將Ⅳ級、Ⅴ級圍巖的膨脹修正系數(shù)取值范圍代入修正公式，對該隧道部分病害區(qū)段圍巖的BQ及圍巖級別進(jìn)行修正，結(jié)果如表6所示。

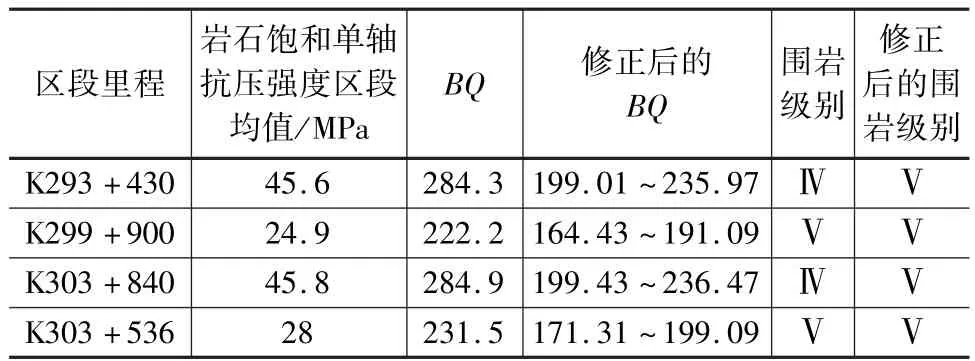
表6 部分病害區(qū)段的石膏質(zhì)巖石修正后BQ分級指標(biāo)

根據(jù)對比可知，相比于規(guī)范中圍巖分級BQ結(jié)果，考慮石膏質(zhì)巖綜合特性修正的BQ值下降了26%～36%；對于Ⅳ級圍巖來說，考慮石膏質(zhì)巖膨脹特性的修正圍巖級別比原BQ對應(yīng)的圍巖級別下降了一級。

8 結(jié)論

本文以穿越石膏質(zhì)巖地層隧道工程為研究背景，對石膏質(zhì)巖膨脹性對圍巖分級的影響進(jìn)行了研究。主要研究內(nèi)容及成果如下:

(1)建立了膨脹壓力簡化計算模型，推導(dǎo)了膨脹壓力解析解；考慮膨脹壓力的影響，對規(guī)范中圍巖壓力與圍巖級別的統(tǒng)計關(guān)系式進(jìn)行了修正，建立了膨脹壓力與圍巖級別的關(guān)系。

(2)考慮洞室跨度和膨脹圍巖范圍，計算了膨脹壓力，對巖性較差的Ⅳ、Ⅴ級圍巖進(jìn)行圍巖級別的修正，發(fā)現(xiàn)膨脹壓力對Ⅳ級圍巖的修正作用更大。

(3)擬合BQ與圍巖級別的函數(shù)關(guān)系，定義了膨脹修正系數(shù)，得到Ⅳ、Ⅴ級圍巖的膨脹修正系數(shù)分別為0.7～0.83、0.74～0.86，建立了考慮膨脹性的石膏質(zhì)圍巖分級修正方法。

(4)通過工程案例證明，考慮石膏質(zhì)巖膨脹性的修正BQ值下降了26%～36%。對于Ⅳ級圍巖，考慮石膏質(zhì)巖綜合特性的修正圍巖級別比原BQ對應(yīng)的圍巖級別下降了一級。