單雙向振動(dòng)條件下飽和軟黏土動(dòng)力特性研究

李 磊,梁 超,鄭 昌,昌志峰,蔣耀晨

(1.浙江交工集團(tuán)股份有限公司,浙江 杭州 310051;2.浙江工業(yè)大學(xué) 土木工程學(xué)院,浙江 杭州 310023)

軟黏土是指在濱海區(qū)域、沼澤地區(qū)和三角洲地帶等水源充沛且水流緩慢的區(qū)域,土體經(jīng)過各種生物化學(xué)反應(yīng)后自然沉降形成的細(xì)粒軟黏性土,其具有壓縮性高、含水率高、抗剪強(qiáng)度低、孔隙比大和滲透性差等特點(diǎn),工程性質(zhì)極為不良。軟黏土在我國(guó)沿海地區(qū)較為常見,隨著沿海地區(qū)的高速發(fā)展,高速公路、鐵路及機(jī)場(chǎng)等基建工程愈發(fā)密集,海上平臺(tái)、人工島等近海工程愈發(fā)多見,以上設(shè)施長(zhǎng)期受交通荷載、波浪荷載和風(fēng)荷載等動(dòng)荷載作用,又多建于深厚軟黏土土層之上,因此對(duì)軟黏土動(dòng)力特性的研究十分必要。

近年來,對(duì)飽和軟黏土的動(dòng)力特性試驗(yàn)研究逐漸增多。基于現(xiàn)有研究成果,循環(huán)加載下飽和細(xì)粒軟黏土土體剛度隨著循環(huán)圈數(shù)的增加而逐漸衰減。基于Idriss等[1]的軟化指數(shù)模型,Matsui等[2]、Yasuhara等[3]、黃娟等[4-5]、周建等[6]和王軍等[7]對(duì)該模型進(jìn)行了考慮動(dòng)應(yīng)力幅值和循環(huán)圈數(shù)的修正。基于Hardin-Drnevich的表達(dá)式[8],張勇等[9]提出了含固結(jié)壓力、動(dòng)應(yīng)力幅值和循環(huán)圈數(shù)等變量的動(dòng)骨干曲線模型。Polito等[10]認(rèn)為不同波形對(duì)能量耗散-孔壓影響關(guān)系不大。目前,國(guó)內(nèi)外學(xué)者主要關(guān)注的還是單向振動(dòng)模式的循環(huán)荷載作用,如交通荷載等。事實(shí)上雙向振動(dòng)模式在工程中也較為常見,如波浪荷載等。雙向振動(dòng)與單向振動(dòng)兩種荷載作用存在不同[11],目前針對(duì)兩者的比較研究還較為少見。王常晶等[12]認(rèn)為單雙向振動(dòng)條件下蕭山軟黏土最小極限循環(huán)強(qiáng)度可視作一致。黃博等[13]對(duì)單雙向振動(dòng)條件下的飽和砂動(dòng)力特性展開研究,提出當(dāng)土樣在較小圈數(shù)下被破壞時(shí),單雙向振動(dòng)模式對(duì)試樣動(dòng)力特性影響較小,兩者可視為等效,而在較大圈數(shù)下,兩者動(dòng)力特性差異明顯。目前,針對(duì)飽和軟黏土的單雙向振動(dòng)對(duì)比試驗(yàn)研究鮮有報(bào)道,因此筆者開展大周數(shù)單雙向振動(dòng)條件下飽和細(xì)粒軟黏土循環(huán)三軸試驗(yàn)研究,主要考慮振動(dòng)模式、循環(huán)圈數(shù)及動(dòng)應(yīng)力幅值等因素對(duì)細(xì)粒軟黏土動(dòng)力特性的影響,并建立考慮振動(dòng)模式和循環(huán)圈數(shù)的軟黏土動(dòng)骨干曲線模型。

1 飽和軟黏土動(dòng)三軸實(shí)驗(yàn)

1.1 試驗(yàn)土樣

試驗(yàn)所用土樣為溫州軟黏土。溫州位于我國(guó)東南,毗鄰東海,是我國(guó)典型的沿海城市。溫州大部分地區(qū)地質(zhì)層多被深厚淤泥質(zhì)軟黏土層占據(jù),厚達(dá)20～30 m,是典型的軟黏土。由于溫州地區(qū)在歷史上未遭遇過劇烈的海平面升降或嚴(yán)重的地表侵蝕,一般認(rèn)為天然溫州軟黏土為正常固結(jié)土。本研究中所用土樣來自溫州地區(qū)一個(gè)深度約10 m的基坑底部。由于重塑土具有較為可靠的可重復(fù)性和均勻性,試驗(yàn)結(jié)果可信度較高,本試驗(yàn)土樣均采用重塑土,該重塑土制備采取泥漿加壓固結(jié)法,具體步驟:1) 將試驗(yàn)所需用土放入烘箱烘干,先用粉碎機(jī)將烘干的土塊碎成小顆粒,再用研磨機(jī)碾磨成粉;2) 根據(jù)1.2倍液限算出所需的土粉和水,稱取定量的干土粉和水混合,用攪拌器攪拌均勻;3) 將泥漿倒入固結(jié)儀中,對(duì)其進(jìn)行12.5,25,50,100 kPa的逐級(jí)加載,每一級(jí)加載后,待土樣壓縮值基本穩(wěn)定后(以壓縮值變化率小于2 mm/d為穩(wěn)定)再施加下一級(jí)荷載,最后一級(jí)荷載加載時(shí)間延長(zhǎng)一周,以待土樣完成主固結(jié)。經(jīng)室內(nèi)試驗(yàn),重塑土的基本物理特性如表1所示。

1.2 試驗(yàn)裝置及試驗(yàn)步驟

試驗(yàn)裝置:為了進(jìn)行復(fù)雜應(yīng)力路徑下飽和細(xì)粒軟黏土的靜動(dòng)力特性試驗(yàn)研究,筆者所采用的試驗(yàn)儀器為英國(guó)GDS公司(GDS Instruments,London)生產(chǎn)的電機(jī)伺服動(dòng)三軸試驗(yàn)系統(tǒng)(圖1)。該設(shè)備具有高精度、高控制力以及可進(jìn)行循環(huán)加載試驗(yàn)的特點(diǎn)。

圖1 電機(jī)伺服動(dòng)三軸試驗(yàn)系統(tǒng)Fig.1 Motor servo triaxial testing system

土動(dòng)力特性室內(nèi)試驗(yàn)常用的方法有動(dòng)三軸試驗(yàn),主要適用于土在較大動(dòng)應(yīng)變幅(ε(γ)>10-4)時(shí)土動(dòng)力特性的測(cè)試,試驗(yàn)步驟:1) 根據(jù)土工試驗(yàn)規(guī)程將重塑土樣制成直徑50 mm、高100 mm的標(biāo)準(zhǔn)圓柱體,周圍貼上濾紙條,以增加排水通道;2) 將切好的土樣裝入GDS動(dòng)三軸壓力室反壓飽和24 h,反壓采用300 kPa,有效圍壓20 kPa,試驗(yàn)土樣飽和度均可達(dá)到98%以上;3) 施加設(shè)定的圍壓完成固結(jié)。

試驗(yàn)分為2個(gè)部分:第1部分為單向振動(dòng)加載試驗(yàn),該試驗(yàn)部分動(dòng)應(yīng)力幅值σa分別為20,30,50 kPa;第2部分為雙向振動(dòng)加載試驗(yàn),該試驗(yàn)部分動(dòng)應(yīng)力幅值σa分別為10,20,30,50 kPa,試驗(yàn)加載頻率均為0.1 Hz。試驗(yàn)加載方式如圖2所示,其中:OAB段表示飽和階段;BCD段表示等壓固結(jié)階段;CD段表示對(duì)應(yīng)固結(jié)圍壓值(本研究固結(jié)圍壓p′=100 kPa);DE段表示動(dòng)力加載階段,單向振動(dòng)加載時(shí)為壓縮波,雙向振動(dòng)加載時(shí)為正弦波。雙向振動(dòng)下動(dòng)應(yīng)力σd=2σa,而在單向振動(dòng)下動(dòng)應(yīng)力σd=σa。具體試驗(yàn)方案見表2。

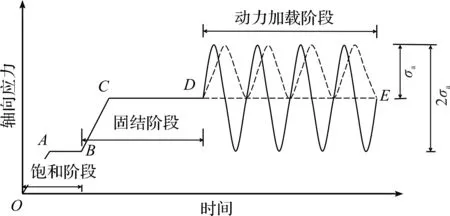
圖2 典型試驗(yàn)加載過程Fig.2 Typical loading process

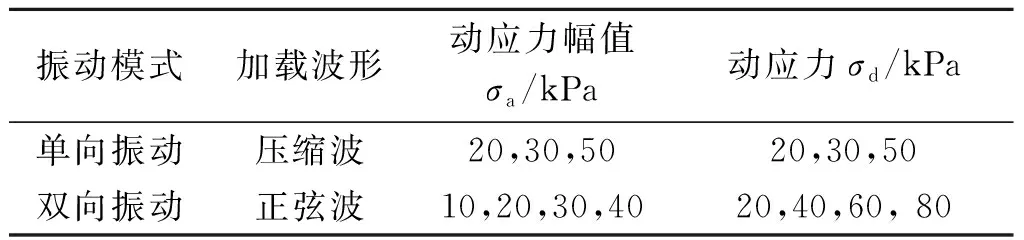
表2 動(dòng)三軸試驗(yàn)方案

2 試驗(yàn)結(jié)果與分析

2.1 孔壓與應(yīng)變發(fā)展

圖3為單雙向振動(dòng)條件下的孔壓時(shí)程曲線。圖3(a)為飽和土樣在不同應(yīng)力水平的雙向振動(dòng)荷載下孔壓時(shí)程曲線,由圖3(a)可知:當(dāng)應(yīng)力水平較小時(shí)(σd分別為20,40 kPa),孔壓在較短時(shí)間內(nèi)迅速完成累積,之后緩慢增長(zhǎng)并趨于平穩(wěn);當(dāng)應(yīng)力水平較高時(shí)(σd=60 kPa),孔壓在早期快速累積然后持續(xù)增長(zhǎng),當(dāng)應(yīng)力水平足夠大時(shí)(σd=80 kPa),孔壓增長(zhǎng)極快,土樣在循環(huán)圈數(shù)N=100時(shí)發(fā)生破壞。圖3(b)為飽和土樣在不同應(yīng)力水平的單向振動(dòng)荷載下孔壓時(shí)程曲線,與雙向振動(dòng)狀態(tài)下的發(fā)展模式類似,在低應(yīng)力狀態(tài)下,單雙向振動(dòng)狀態(tài)下的孔壓極為相近,單向振動(dòng)孔壓略大于雙向振動(dòng)。

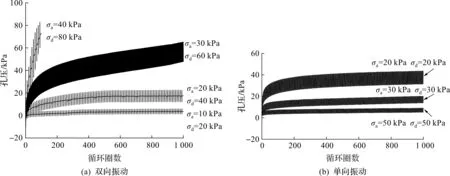
圖3 單雙向振動(dòng)狀態(tài)下孔壓時(shí)程曲線Fig.3 Development of pore pressure under one-way and two-way cyclic loading

圖4為單雙向振動(dòng)下N=1 000時(shí)的孔壓與應(yīng)力水平關(guān)系曲線。圖4(a)為孔壓與動(dòng)應(yīng)力的關(guān)系曲線,在相同的動(dòng)應(yīng)力下,單向振動(dòng)的孔壓比雙向振動(dòng)大;圖4(b)為孔壓與動(dòng)應(yīng)力幅值的關(guān)系曲線,在相同的動(dòng)應(yīng)力幅值下,孔壓的結(jié)果則與上述結(jié)果剛好相反。結(jié)果表明不同的振動(dòng)模式對(duì)孔壓的累積有顯著影響。

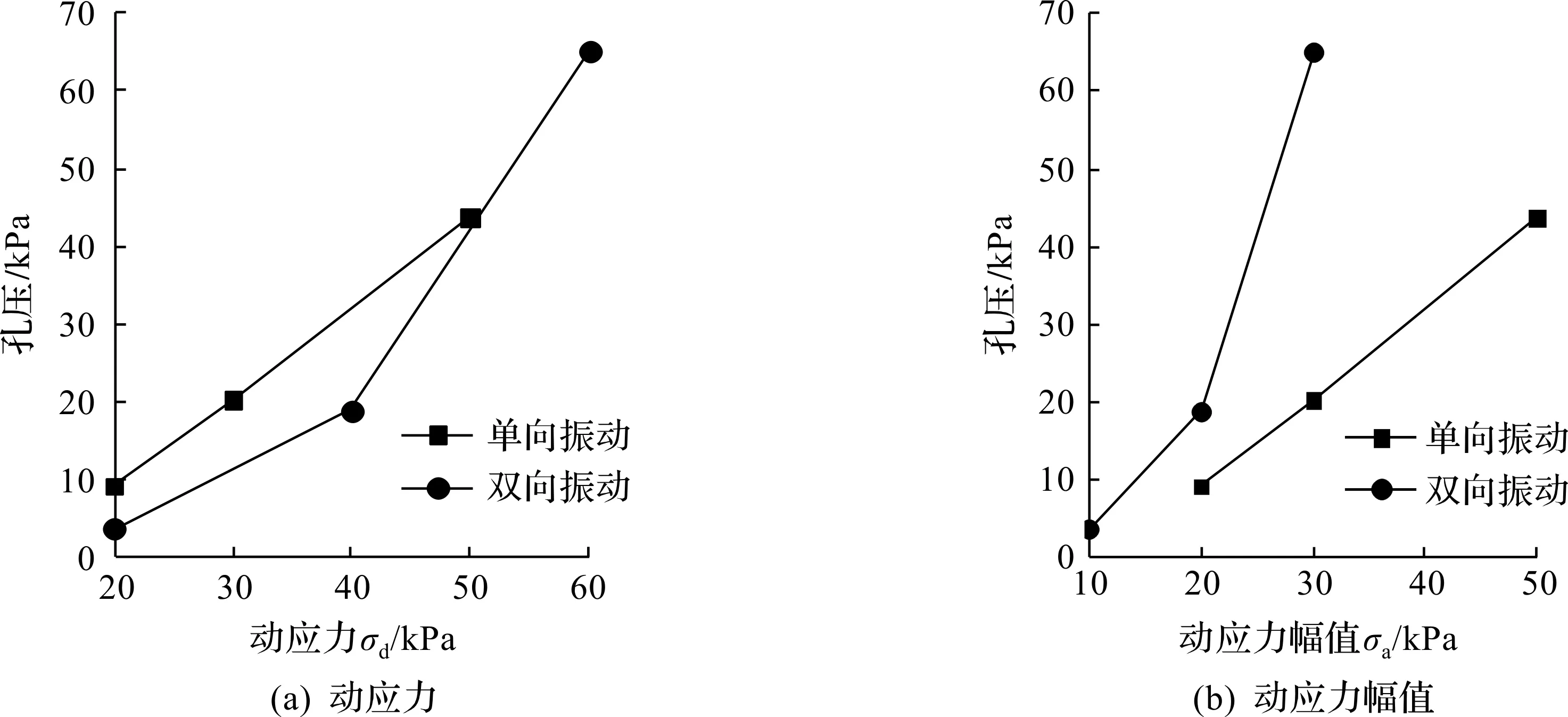
圖4 單雙向振動(dòng)下典型圈數(shù)孔壓對(duì)比Fig.4 Development of pore pressure under one-way and two-way cyclic loading

圖5為單雙向振動(dòng)條件下的動(dòng)應(yīng)變時(shí)程曲線。圖5(a,b)分別為飽和土樣在不同應(yīng)力水平的雙向和單向振動(dòng)荷載下動(dòng)應(yīng)變時(shí)程曲線。圖5(a)中,在低應(yīng)力水平下,土體迅速達(dá)到安定狀態(tài),循環(huán)圈數(shù)對(duì)土體形變累積影響很小。當(dāng)σa=10 kPa時(shí),動(dòng)應(yīng)變?chǔ)興為0.034 7%,隨著圈數(shù)增加,動(dòng)應(yīng)變幾乎沒有增長(zhǎng)。隨著應(yīng)力增大,循環(huán)荷載對(duì)土體擾動(dòng)加劇,當(dāng)應(yīng)力水平超過某一臨界值,如當(dāng)σa=40 kPa時(shí),土樣在短時(shí)間內(nèi)發(fā)生疲勞破壞。圖5(b)中,土樣均處于安定狀態(tài),且隨動(dòng)應(yīng)力幅值逐漸增加,土樣應(yīng)變對(duì)應(yīng)增大。當(dāng)σa=50 kPa時(shí),土樣仍未破壞。說明振動(dòng)模式對(duì)土樣的應(yīng)變發(fā)展有顯著影響。對(duì)比圖5(a,b)可知:在相同動(dòng)應(yīng)力幅值下,雙向振動(dòng)狀態(tài)下的動(dòng)應(yīng)變比單向振動(dòng)狀態(tài)下的動(dòng)應(yīng)變大,如在動(dòng)應(yīng)力幅值均為20 kPa時(shí),雙向條件下的動(dòng)應(yīng)變是單向振動(dòng)條件下的2.04倍。

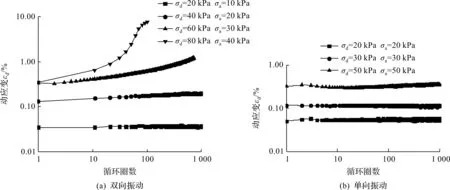
圖5 單雙向振動(dòng)狀態(tài)下動(dòng)應(yīng)變時(shí)程曲線Fig.5 Development of dynamic strain under one-way and two-way cyclic loading

圖6為單雙向振動(dòng)下N=100時(shí)的動(dòng)應(yīng)變與應(yīng)力的關(guān)系曲線。圖6(a)為動(dòng)應(yīng)變與動(dòng)應(yīng)力的關(guān)系,在相同的動(dòng)應(yīng)力下,單向振動(dòng)的動(dòng)應(yīng)變比雙向振動(dòng)大;圖6(b)為動(dòng)應(yīng)變與應(yīng)力幅值的關(guān)系曲線,在相同應(yīng)力幅值下,單向振動(dòng)下的動(dòng)應(yīng)變明顯比雙向振動(dòng)大。結(jié)果表明不同的振動(dòng)模式對(duì)土體的應(yīng)變發(fā)展有顯著影響。

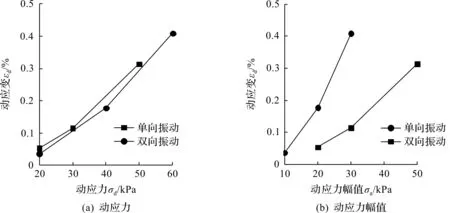
圖6 單雙向振動(dòng)下典型圈數(shù)動(dòng)應(yīng)變比較Fig.6 Comparison of dynamic strains under one-way and two-way cyclic loading at typical cycle number

2.2 應(yīng)力—應(yīng)變關(guān)系

安定是指結(jié)構(gòu)體在某一特定的循環(huán)荷載下,產(chǎn)生的塑性變形在有限的循環(huán)次數(shù)后穩(wěn)定下來,且在安全界限內(nèi),結(jié)構(gòu)體不會(huì)發(fā)生破壞[14]。在彈塑性安定狀態(tài)時(shí),動(dòng)應(yīng)力—?jiǎng)討?yīng)變關(guān)系曲線可基本看為一個(gè)封閉且中心對(duì)稱的滯回圈,稱為滯回曲線。

圖7為在典型圈數(shù)下的滯回圈對(duì)比,圖中Ed和E′d分別為單向與雙向振動(dòng)下的滯回圈斜率。單向振動(dòng)狀態(tài)下滯回圈呈狹長(zhǎng)的紡錘形,且滯回圈的面積隨著循環(huán)圈數(shù)的增加逐漸減小,而雙向振動(dòng)狀態(tài)下的滯回圈呈現(xiàn)明顯的棘輪效應(yīng),隨著荷載作用次數(shù)的增加,塑性變形越來越大,棘輪效應(yīng)愈加明顯,滯回圈面積也逐漸增大。此外,由于單向振動(dòng)條件下試樣處于彈塑性安定狀態(tài),隨著循環(huán)荷載的增加,孔壓與累積應(yīng)變幾乎不再增加,滯回圈重合,滯回圈的斜率無明顯變化,土樣的動(dòng)模量幾乎不變,雙向振動(dòng)狀態(tài)下滯回圈的斜率隨振動(dòng)圈數(shù)的增加而減小,與圖5中應(yīng)變時(shí)程曲線結(jié)果相符。在循環(huán)加荷載初期滯回圈比較陡峭,隨著圈數(shù)的增加,滯回圈的斜率逐漸降低,這種情況體現(xiàn)了土體在循環(huán)荷載作用下的剛度軟化性。

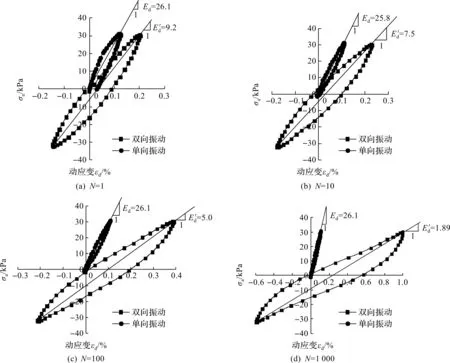
圖7 典型圈數(shù)下σa=30 kPa時(shí)單雙向振動(dòng)條件下滯回圈對(duì)比Fig.7 Comparison of hysteretic loops under one-way and two-way cyclic loading at σa=30 kPa at typical cycle number

比較各典型振次下的單雙向振動(dòng)條件下滯回圈可以發(fā)現(xiàn):在相同加載圈數(shù)和相同應(yīng)力幅值下,單向振動(dòng)條件下的滯回圈斜率大于雙向振動(dòng)條件下的滯回圈斜率,即單向振動(dòng)下動(dòng)模量大。在相同圈數(shù)下雙向振動(dòng)時(shí)土樣產(chǎn)生的應(yīng)變比單向振動(dòng)時(shí)土樣產(chǎn)生的應(yīng)變大,這是由于在雙向振動(dòng)條件下,土樣額外受到擠伸作用,而單向振動(dòng)時(shí)只有壓應(yīng)力,所以在雙向振動(dòng)時(shí)土樣產(chǎn)生的應(yīng)變大。

2.3 骨干曲線

骨干曲線是受同一固結(jié)壓力的土在不同動(dòng)應(yīng)力作用下每一周期應(yīng)力—應(yīng)變關(guān)系曲線滯回圈頂點(diǎn)的連線,同時(shí)也反映了動(dòng)應(yīng)力對(duì)動(dòng)應(yīng)變的非線性,結(jié)果如圖8所示。對(duì)于骨干曲線,曲線上每一個(gè)點(diǎn)的動(dòng)應(yīng)力τd和動(dòng)應(yīng)變?chǔ)胐均為各自的幅值,其曲線形態(tài)接近雙曲線,一般比較容易描述。Hardin等[8]提出了目前兩種常用的骨干曲線表達(dá)方式。

圖8 骨干曲線Fig.8 Diagram of backbone curve

通常,采用Hardin-Drnevich的σd-εd曲線(雙曲線關(guān)系)[8]來分析循環(huán)荷載作用下土體的動(dòng)應(yīng)力—?jiǎng)討?yīng)變關(guān)系的骨干曲線,即

(1)

故可得動(dòng)壓縮模量函數(shù)的基本關(guān)系為

(2)

式中:σd,εd分別為動(dòng)應(yīng)力幅值和彈性應(yīng)變;a,b為試驗(yàn)參數(shù)。進(jìn)一步分析上述兩式,可得a,b的物理意義,a為最大剪切模量的倒數(shù),b為最大應(yīng)力幅值的倒數(shù)。

圖9為單雙向振動(dòng)條件下不同循環(huán)圈數(shù)下所對(duì)應(yīng)的動(dòng)應(yīng)力—?jiǎng)討?yīng)變關(guān)系的骨干曲線,從骨干曲線中可以看到:在不同振動(dòng)模式下,土體都表現(xiàn)出了應(yīng)變軟化的特點(diǎn),并且骨干曲線隨圈數(shù)的增加而右移,初始斜率減小,表明了土樣剛度循環(huán)衰減的過程。比較圖9中單雙向振動(dòng)條件下的骨干曲線可以發(fā)現(xiàn):單向振動(dòng)條件下的骨干曲線比雙向振動(dòng)條件下的骨干曲線高,且單向振動(dòng)條件下的初始斜率比雙向振動(dòng)條件下的初始斜率高。說明土樣在單向振動(dòng)條件下的抗剪強(qiáng)度和剛度均比雙向振動(dòng)條件下高,此結(jié)論表明振動(dòng)模式對(duì)土樣的強(qiáng)度和剛度都有不可忽視的影響。

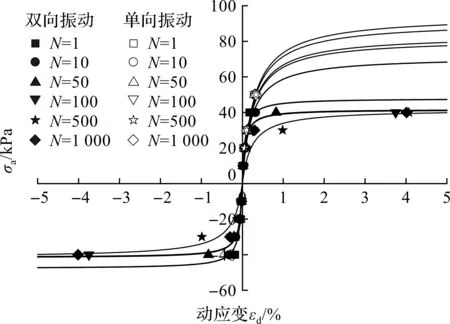
圖9 單雙向振動(dòng)條件下不同圈數(shù)擬合骨干曲線Fig.9 Backbone curves fitted with test results at different typicalcycle numbers under one-way and two-way cyclic loading

2.4 考慮循環(huán)振次的動(dòng)骨干曲線模型

由圖10(a,b)擬合的動(dòng)應(yīng)力—?jiǎng)討?yīng)變骨干曲線參數(shù)可建立不同循環(huán)圈數(shù)下的動(dòng)骨干曲線模型。圖10(a)為雙向振動(dòng)下骨干曲線方程參數(shù)b1與循環(huán)圈數(shù)的關(guān)系曲線,圖10(b)為單向振動(dòng)下骨干曲線方程參數(shù)b2與循環(huán)圈數(shù)的關(guān)系曲線。擬合參數(shù)b1和b2與循環(huán)圈數(shù)N之間的關(guān)系可表示為

b1=n1-n2·ln(N+n3)

(3)

b2=m1-m2·ln(N+m3)

(4)

式中:n1=0.020 64;n2=-0.000 68;n3=0.23;m1=0.002 322;m2=-0.001 236;m3=12.207;N為循環(huán)圈數(shù)。

圖10(a,b)中的曲線為式(1)擬合所得的擬合曲線,該擬合曲線能夠較為準(zhǔn)確地表達(dá)擬合參數(shù)b與循環(huán)圈數(shù)的關(guān)系。表3,4中數(shù)據(jù)是根據(jù)式(1,2)與Hardin-Drnevich雙曲線模型擬合所得,圖10中兩種振動(dòng)模式下骨干曲線的初始斜率接近,a1,a2變化極小,因此直接作為常數(shù)。

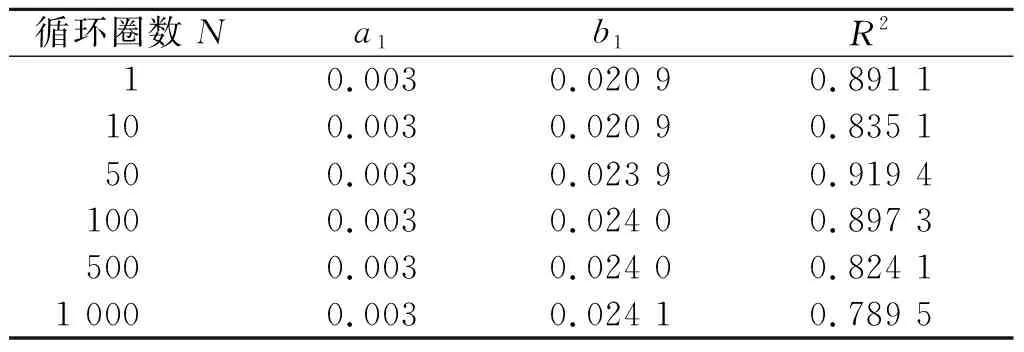
表3 雙向振動(dòng)條件下擬合參數(shù)

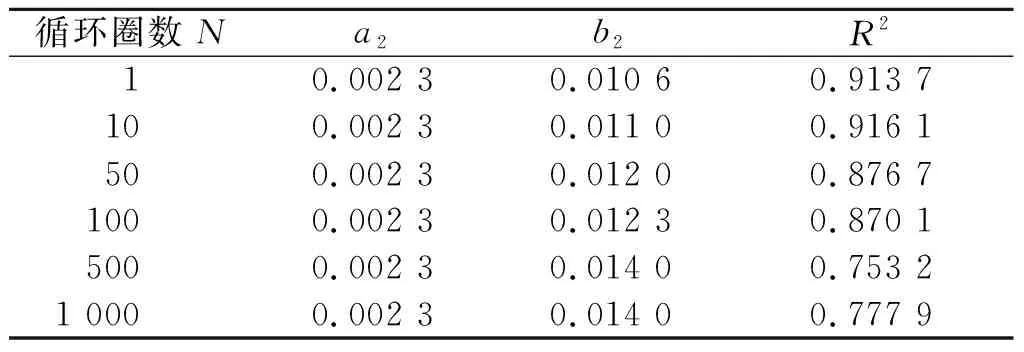
表4 單向振動(dòng)條件下擬合參數(shù)

將式(3)代入式(1)中,便可得到不同振動(dòng)模式下不同循環(huán)圈數(shù)的動(dòng)骨干曲線方程,即

(5)

(6)

式中:a1=0.003;n1=0.020 64;n2=-0.000 68;n3=0.23;a2=0.002 3;m1=0.002 322;m2=-0.001 236;m3=12.207。

比較單雙向振動(dòng)條件下的擬合參數(shù)b,可發(fā)現(xiàn)雙向振動(dòng)條件下的a,b均大于單向振動(dòng)條件下的a,b,表示同等條件下,單向振動(dòng)下土體的剛度和強(qiáng)度均比雙向振動(dòng)條件下的剛度大,與前文中的結(jié)論一致。

圖11(a,b)分別為雙向和單向振動(dòng)狀態(tài)下實(shí)驗(yàn)值與預(yù)測(cè)值N—εd的關(guān)系曲線。比較圖11(a,b)中的實(shí)驗(yàn)值與預(yù)測(cè)值可以發(fā)現(xiàn):本研究動(dòng)骨干曲線模型對(duì)實(shí)驗(yàn)值的預(yù)測(cè)較為準(zhǔn)確。通過以下公式可以得到預(yù)測(cè)的N—εd曲線,即

(7)

(8)

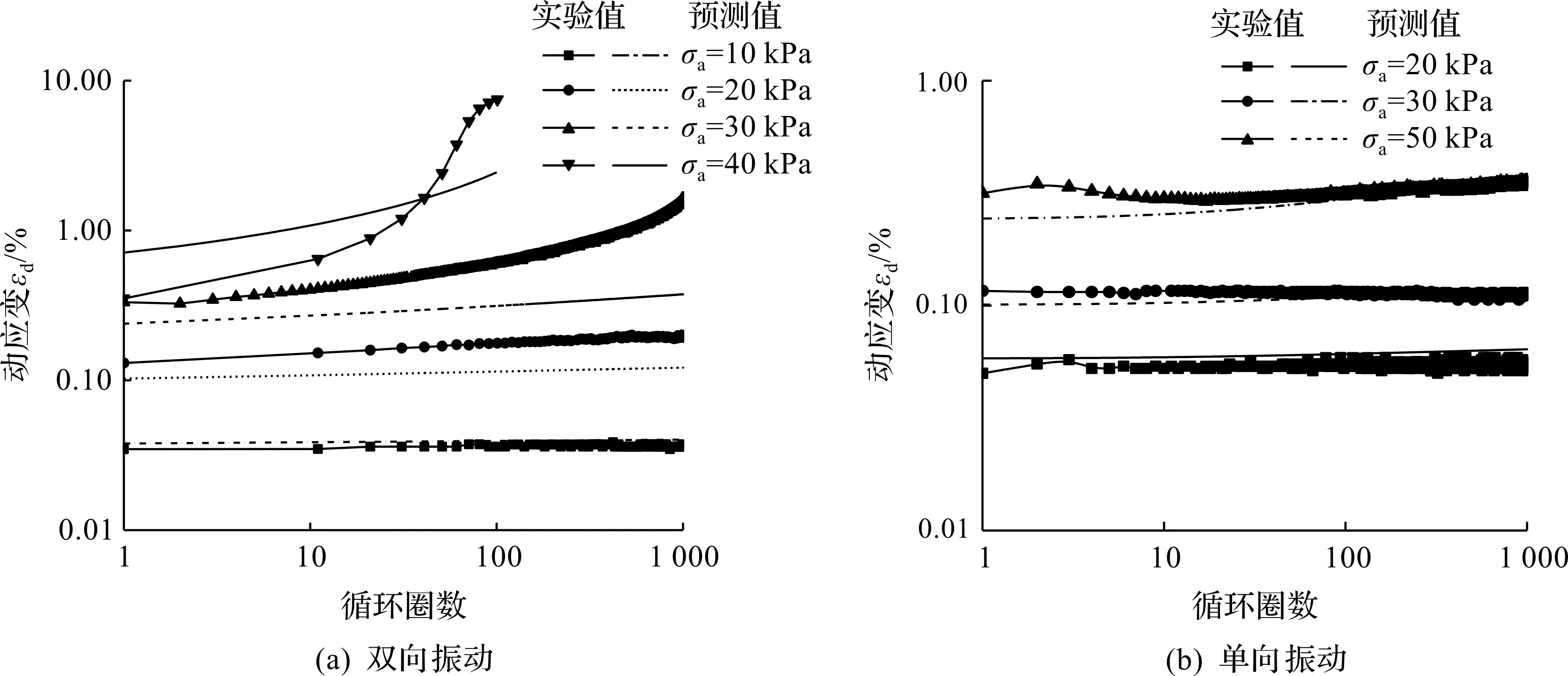
圖11 單雙向振動(dòng)狀態(tài)下實(shí)驗(yàn)值與預(yù)測(cè)值對(duì)比Fig.11 Comparison of measured and predicted dynamic strains under one-way and two-way cyclic loading

從以上模型的建立過程可以看出:筆者構(gòu)建的動(dòng)骨干曲線考慮了循環(huán)圈數(shù)的影響,對(duì)于循環(huán)荷載下易發(fā)生軟化現(xiàn)象的飽和軟黏土來說,該模型更符合實(shí)際。考慮到不同振動(dòng)模式對(duì)土體的影響有所不同,筆者分別建立并比較了單雙向兩種不同振動(dòng)模式下的骨干曲線模型。

3 結(jié) 論

不同的單雙向振動(dòng)模式對(duì)循環(huán)荷載下飽和軟黏土應(yīng)變發(fā)展有顯著影響。在相同動(dòng)應(yīng)力下,單向振動(dòng)導(dǎo)致的動(dòng)應(yīng)變比雙向振動(dòng)略大,而在相同應(yīng)力幅值下,單向振動(dòng)導(dǎo)致的動(dòng)應(yīng)變明顯比雙向振動(dòng)小。在飽和軟黏土的動(dòng)應(yīng)力—?jiǎng)討?yīng)變骨干曲線中,土體初始剛度及動(dòng)強(qiáng)度隨循環(huán)圈數(shù)的增大均有所減小。同等條件下,單向振動(dòng)下土體的剛度和強(qiáng)度均比雙向振動(dòng)條件下的剛度大。考慮到不同振動(dòng)模式對(duì)土體的影響有所不同,分別建立并比較了單雙向兩種不同振動(dòng)模式下的骨干曲線模型,模型考慮了動(dòng)應(yīng)力幅值和循環(huán)圈數(shù)的影響,所得預(yù)測(cè)值與實(shí)驗(yàn)值較為吻合。